利用二维码定位技术实现桌面机器人简易定位方案（下篇）

1、前言

机械手臂尤其是工业场景下大部分的应用是在一个平面（桌面）内完成一些抓取工作。一般可以用示教方式完成重复步骤。但是示教方式，对于一些活动的工件，或者相对比较开放的环境，不太适用，很多通过视觉来做定位。视觉定位最为稳定的要数二维码的识别，这个已经被无数行业场景所验证。
二维码定位本质上是轮廓监测及内外轮廓的固定关联关系的识别，以及基于平面的仿射变换：
二维码的定位原理是使用特定的图案和编码方式，在图像中确定二维码的位置和方向。二维码通常由多个小方块组成，其中包含了黑白相间的信息编码。
二维码的定位图案通常是一个大的正方形，内部包含了更小的正方形。这些小正方形被称为定位标记，用来表示二维码的位置和方向。定位标记的位置和大小是固定的，一般位于二维码的四个角落，用来确定二维码的边界。
我们可以在桌面机器人视觉定位中创造属于自己的类二维码定位框。这样就可以在精度要求不高的情况下稳定应用。
上篇我们把利用二维码定位技术的原理用于工作桌面平面定位的原理。在本篇继续完成实际应用工作。

2、定位标签定义

为了便于实操，我们在A4纸上三个定位标签并打印出来（打印资源见文后链接），效果如下：

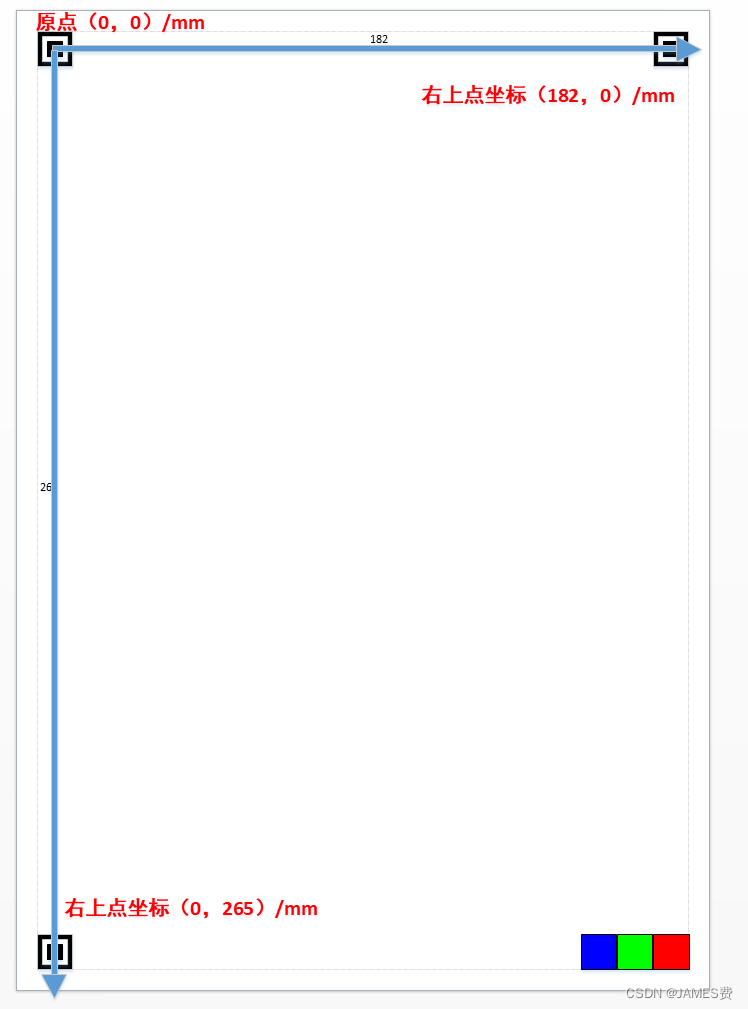
测量实际的距离，左上右上的距离为182（或192）mm，（根据打印机设置以实际测量为准）:

测量实际左上和左下的距离为265（或284）mm（根据打印机设置以实际测量为准）：

我们可以定义坐标系如下：

根据以上三个定位点的位置关系，我们可以组织识别算法，可以在摄像头最准A4或（桌面）的任意旋转角度下，实现识别和定位。

3、识别算法流程

根据如上定位标签的几何关系特征，我们可以按照如下流程识别三个标签的位置，分别识别出哪个标签是左上，哪个标签是右上，哪个标签是左下。流程如下：

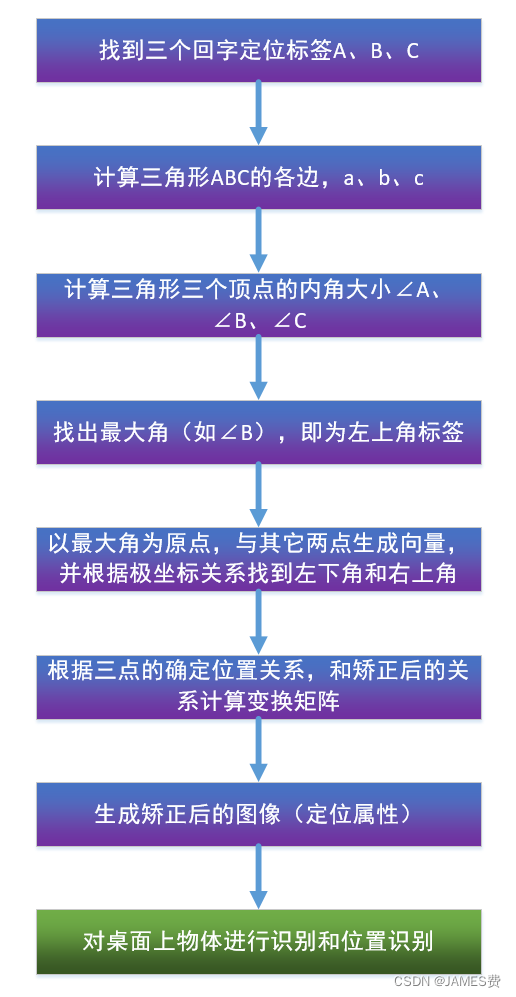
如上所示，按照三个点（A，B,C）组成的三角形，计算三条边，然后根据余弦公式，求出三角形的三个内角。可以看到，内角最大的一个就是我们的左上角的定位点(假如是B)。找到左上角定位点后，我们可以生成向量BA，和向量BC，然后可以根据两个向量的旋转关系得到哪个是右上角，哪个是左下角，如下图所示，α角为向量BA与x轴的夹角，β角是向量BC与x轴的夹角，可以看到根据角度和边长的关系，我们可以唯一确定哪个是右上角，哪个是左下角：

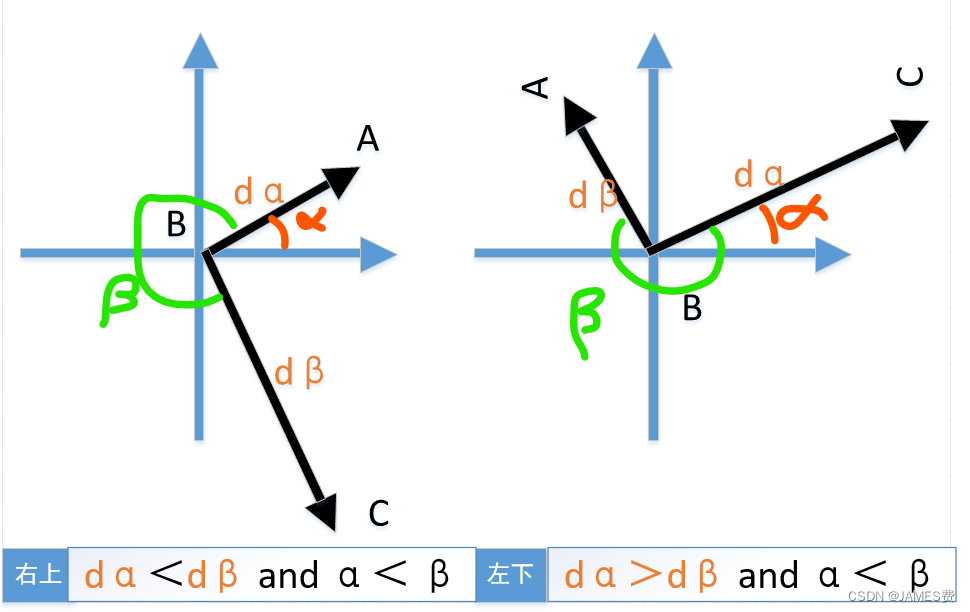
以上给出了两种情况，前提条件是将向量的与x轴的夹角转化到0~2pi的范围内。
根据第2节的标签位置定义，我们可以知道：dα/dβ趋向197/296或296/197

4、python编程

根据以上算法流程和思路，我们就可以用python实现了：

4.1 查找三个回字定位点python

以下程序是用于查找图片中的三个定位标签，存储到一个landmark_list的数组中。

	#读取图像
	image = cv2.imread('demo1.jpg')
    image = cv2.resize(image, (0, 0), fx=0.5, fy=0.5)
    cv2.imshow('sourceimg', image)

    # 转灰度、二值化、找轮廓
    gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)    
    _, thresh = cv2.threshold(gray, 100, 255,  cv2.THRESH_BINARY_INV)
    #查找轮廓    
    contours, hir = cv2.findContours(thresh, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE)

    # 定位标签存储
    landmark_list = []
    grandson_list = []
    landmark_centers=[]

    # 通过层级信息查找“回”字特征定位标签
    for index, landmark in enumerate(hir[0]):  # 查找最外层（A）轮廓        
        if landmark[2] != -1:#有儿子轮廓            
            son_index = landmark[2] 
            if hir[0][son_index][2]!=-1:#有孙子轮廓
                grandson_index=hir[0][son_index][2]                
                if hir[0][grandson_index][2]==-1:#没有子轮廓
                    
                    if cv2.arcLength(contours[grandson_index], True)<=0.0001:
                        pass
                    else:
                        dratio = cv2.arcLength(contours[index], True) / cv2.arcLength(contours[grandson_index], True)
                        #当回字形的内外轮廓比在2和3之间，人为是定位点
                        if 2 < dratio< 3:
                            landmark_list.append(landmark)
                            grandson_list.append(contours[grandson_index])
                            x, y, w, h = cv2.boundingRect(contours[grandson_index])
                            cx,cy=x + w//2, y + h//2
                            landmark_centers.append((cx,cy))
                           
     
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

4.2 根据三个定位点坐标位置关系，进行识别python

当获得定位点后，就可以按照上一节的原理进行识别，识别出哪个是左上角，哪个是右上角，哪个是左下角。
代码如下：

def find3P(points):
    #依次找到3个定位点顺序，右上，左上，左下
    if len(points)!=3:
        print("no 3 landmarks or more than 3")
        return False,None
    
    
    # 计算三个顶点对应的内角
    angles = []
    vectors=[]#向量1   
    pps=[[0,0],[0,0],[0,0]]#依次存储右上，左上，左下点
    for i in range(3):
        p1 = points[i]
        p2 = points[(i + 1) % 3]
        p3 = points[(i + 2) % 3]
        a = math.sqrt((p2[0] - p3[0])**2 + (p2[1] - p3[1])**2)
        b = math.sqrt((p1[0] - p3[0])**2 + (p1[1] - p3[1])**2)
        c = math.sqrt((p1[0] - p2[0])**2 + (p1[1] - p2[1])**2)
        angle = math.acos((c**2 + b**2 - a**2) / (2 * c * b))
        angles.append(angle)
        vector0= [p3[0]-p1[0],-p3[1]+p1[1]]#转化为xy坐标系
        vector1= [p2[0]-p1[0],-p2[1]+p1[1]]
        vectors.append([vector0,vector1])
    
    # 找出最大的内角对应的顶点
    left_top_index=angles.index(max(angles))
    pps[1]=[points[left_top_index][0] ,-points[left_top_index][1]]
    # 找出right top对应的顶点,与x轴夹角最大
    vector0,vector1=vectors[left_top_index]
    dtheta=cartesian_to_polar(vector1)-cartesian_to_polar(vector0) 
    
    #长度比检测
    if vector_magnitude(vector1)>vector_magnitude(vector0):
        if vector_magnitude(vector1)/vector_magnitude(vector0)<1.4:
            print("ratio wrong")
            return False,None
    else:
        if vector_magnitude(vector0)/vector_magnitude(vector1)<1.4:
            print("ratio wrong")
            return False,None

    
    if dtheta>math.pi :
        #大于pi，说明为左下角
        if vector_magnitude(vector1)/vector_magnitude(vector0)>1.4:
            pps[0]=[vector0[0]+pps[1][0],vector0[1]+pps[1][1]]
            pps[2]=[vector1[0]+pps[1][0],vector1[1]+pps[1][1]]
        else:
            pps[2]=[vector0[0]+pps[1][0],vector0[1]+pps[1][1]]
            pps[0]=[vector1[0]+pps[1][0],vector1[1]+pps[1][1]]
            
    else:
        #小于0，说明为右上角
        if vector_magnitude(vector0)/vector_magnitude(vector1)>1.4:
            pps[2]=[vector0[0]+pps[1][0],vector0[1]+pps[1][1]]
            pps[0]=[vector1[0]+pps[1][0],vector1[1]+pps[1][1]]
        else:
            pps[0]=[vector0[0]+pps[1][0],vector0[1]+pps[1][1]]
            pps[2]=[vector1[0]+pps[1][0],vector1[1]+pps[1][1]]
            
    
    for i in range(3):
        #转回图像坐标系
        pps[i][1]=int(-pps[i][1])
        pps[i][0]=int(pps[i][0])
    
    return True,pps
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67

4.3 根据实际坐标对当前图像进行矫正python

当得到三个点的确切位置后，就可以利用opencv自带的cv2.getAffineTransform函数进行矫正。

PS:cv2.getAffineTransform是OpenCV库中的一个函数，用于获取仿射变换矩阵。仿射变换是一种二维几何变换，可以通过平移、旋转、缩放和剪切等操作来改变图像的形状和位置。

该函数需要输入三个点的坐标，这三个点分别是原始图像中的三个点和目标图像中对应的三个点。根据这些点的坐标关系，cv2.getAffineTransform函数会计算出一个2x3的仿射变换矩阵。

这个仿射变换矩阵可以用于对原始图像进行变换，使得原始图像中的三个点在目标图像中的位置与给定的目标点一致。通过cv2.warpAffine函数可以将原始图像进行仿射变换。

代码如下：

		#定义以真实的A4值上的三个坐标点，从右上、左上、左下三个点，一个像素代表1mm，为了显示方便查看我们把图像放大ratio倍
		realpoints=[[(10+182)*ratio, 10*ratio], [10*ratio, 10*ratio], [10*ratio, (10+265)*ratio]]    
		src_pts = np.array([pp3[0],pp3[1],pp3[2]], dtype="float32")
        dst_pts = np.array(realpoints, dtype="float32")
        #获取变换矩阵
        M = cv2.getAffineTransform(src_pts, dst_pts)
        #根据变换矩阵，得到矫正后的图像
        Rbackimg = cv2.warpAffine(image, M, (227*ratio, 324*ratio))
        #...
1
2
3
4
5
6
7
8
9

至此我们得到了矫正后的图像：
原来的图像：

矫正后的图像，可以看到跟我们开始打印的图像是一致了：

4.4 计算物体的坐标值python

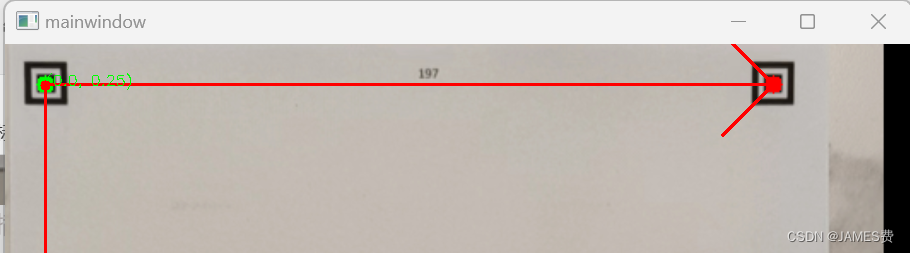
在以上的基础上，我们就可以加入物体识别算法，如YOLO，或者颜色查找等算法获取物体的坐标，然后简单转化到实际坐标，这里我们直接用鼠标去点击矫正后的图像，直接输出指定位置的实际坐标：

如上图，点击物体，可以得出在真实坐标系下的坐标为（81.5，112.0）
分别点击三个点附近的点，可以看到，输出跟实际真实坐标分别是（182，0），（0，0），（0，265）相差不大。

总结

通过二维码定位技术，我们可以方便构建桌面视觉物体识别的坐标系统，并可以结合机械臂进行抓取。
后续，我们可以配合一些图像识别算法，实现物体的识别，并结合机械臂进行抓取。注意，此种方法在摄像头与桌面不平衡度大时，远离左上点部分会产生较大误差。因此，摄像机的摆放尽量要与桌面（A4）值平行。

本篇对应python源码

所有python源码，和A4打印文件已经上传，地址如下：地址
或进公众号获取。