sklearn实战03：特征工程和预处理_特征工程处理产品预测问题

1 概述

1.1 数据挖掘流程

1. 获取数据
2. 数据预处理
   数据预处理是从数据中检测，纠正或删除损坏，不准确或不适用于模型的记录的过程
   可能面对的问题有：数据类型不同，比如有的是文字，有的是数字，有的含时间序列，有的连续，有的间断。也可能，数据的质量不行，有噪声，有异常，有缺失，数据出错，量纲不一，有重复，数据是偏态，数据量太大或太小
   数据预处理的目的：让数据适应模型，匹配模型的需求
3. 特征工程：
   特征工程是将原始数据转换为更能代表预测模型的潜在问题的特征的过程，可以通过挑选最相关的特征，提取特征以及创造特征来实现。其中创造特征又经常以降维算法的方式实现。
   可能面对的问题有：特征之间有相关性，特征和标签无关，特征太多或太小，或者干脆就无法表现出应有的数据现象或无法展示数据的真实面貌。
   特征工程的目的：1) 降低计算成本，2) 提升模型上限
4. 建模，测试模型并预测出结果
5. 上线，验证模型效果

1.2 sklearn中的数据预处理和特征工程

模块preprocessing：几乎包含数据预处理的所有内容
模块Impute：填补缺失值专用
模块feature_selection：包含特征选择的各种方法的实践
模块decomposition：包含降维算法

2 数据预处理 Preprocessing & Impute

2.1 数据无量纲化

将不同规格的数据转换到同一规格，或不同分布的数据转换到某个特定分布的需求，这种需求统称为将数据“无量纲化”。譬如梯度和矩阵为核心的算法中，譬如逻辑回归，支持向量机，神经网络，无量纲化可以加快求解速度；而在距离类模型，譬如K近邻，K-Means聚类中，无量纲化可以帮我们提升模型精度，避免某一个取值范围特别大的特征对距离计算造成影响。（一个特例是决策树和树的集成算法们，对决策
树我们不需要无量纲化，决策树可以把任意数据都处理得很好。）
数据的无量纲化可以是线性的，也可以是非线性的。线性的无量纲化包括中心化（Zero-centered或者Meansubtraction）处理和缩放处理（Scale）。中心化的本质是让所有记录减去一个固定值，即让数据样本数据平移到某个位置。缩放的本质是通过除以一个固定值，将数据固定在某个范围之中，取对数也算是一种缩放处理.

2.1.1 preprocessing.MinMaxScaler

当数据(x)按照最小值中心化后，再按极差（最大值 - 最小值）缩放，数据移动了最小值个单位，并且会被收敛到
[0,1]之间，而这个过程，就叫做数据归一化(Normalization，又称Min-Max Scaling)。注意，Normalization是归
一化，不是正则化，真正的正则化是regularization，不是数据预处理的一种手段。归一化之后的数据服从正态分
布，公式如下：

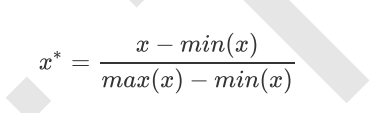
在sklearn当中，我们使用preprocessing.MinMaxScaler来实现这个功能。MinMaxScaler有一个重要参数，
feature_range，控制我们希望把数据压缩到的范围，默认是[0,1]。

2.1.2 preprocessing.StandardScaler

当数据(x)按均值(μ)中心化后，再按标准差(σ)缩放，数据就会服从为均值为0，方差为1的正态分布（即标准正态分
布），而这个过程，就叫做数据标准化.

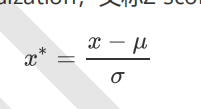
对于StandardScaler和MinMaxScaler来说，空值NaN会被当做是缺失值，在fit的时候忽略，在transform的时候
保持缺失NaN的状态显示。并且，尽管去量纲化过程不是具体的算法，但在fit接口中，依然只允许导入至少二维数
组，一维数组导入会报错。通常来说，我们输入的X会是我们的特征矩阵，现实案例中特征矩阵不太可能是一维所
以不会存在这个问题。

2.1.3 StandardScaler和MinMaxScaler选哪个？

大多数机器学习算法中，会选择StandardScaler来进行特征缩放，因为MinMaxScaler对异常值非常敏
感。在PCA，聚类，逻辑回归，支持向量机，神经网络这些算法中，StandardScaler往往是最好的选择。
MinMaxScaler在不涉及距离度量、梯度、协方差计算以及数据需要被压缩到特定区间时使用广泛，比如数字图像
处理中量化像素强度时，都会使用MinMaxScaler将数据压缩于[0,1]区间之中。

2.2 缺失值

2.2.1 impute.SimpleImputer

class sklearn.impute.SimpleImputer (missing_values=nan, strategy=’mean’, fill_value=None, verbose=0,copy=True)

from sklearn.impute import SimpleImputer
imp_mean = SimpleImputer() #实例化，默认均值填补
imp_median = SimpleImputer(strategy="median") #用中位数填补
imp_0 = SimpleImputer(strategy="constant",fill_value=0) #用0填补
imp_mean = imp_mean.fit_transform(Age) #fit_transform一步完成调取结果
imp_median = imp_median.fit_transform(Age)
imp_0 = imp_0.fit_transform(Age)
#在这里我们使用中位数填补Age
data.loc[:,"Age"] = imp_median
1
2
3
4
5
6
7
8
9

使用python填充

data.loc[:,"Age"] = data.loc[:,"Age"].fillna(data.loc[:,"Age"].median())
#.fillna 在DataFrame里面直接进行填补
1
2

2.3 处理分类型特征：编码与哑变量

2.3.1 preprocessing.LabelEncoder

标签专用，能够将分类转换为分类数值

from sklearn.preprocessing import LabelEncoder
data.iloc[:,-1] = LabelEncoder().fit_transform(data.iloc[:,-1])#要输入的是标签，不是特征矩阵，所以允许一维
1
2

2.3.2 preprocessing.OrdinalEncoder

特征专用，能够将分类特征转换为分类数值
如果特征矩阵中有空值，会报错

2.3.3 preprocessing.OneHotEncoder：独热编码，创建哑变量

我们刚才已经用OrdinalEncoder把分类变量Sex和Embarked都转换成数字对应的类别了。在舱门Embarked这一
列中，我们使用[0,1,2]代表了三个不同的舱门，然而这种转换是正确的吗？
我们来思考三种不同性质的分类数据：
1） 舱门（S，C，Q）
三种取值S，C，Q是相互独立的，彼此之间完全没有联系，表达的是S≠C≠Q的概念。这是名义变量。
2） 学历（小学，初中，高中）
三种取值不是完全独立的，我们可以明显看出，在性质上可以有高中>初中>小学这样的联系，学历有高低，但是学
历取值之间却不是可以计算的，我们不能说小学 + 某个取值 = 初中。这是有序变量。
3） 体重（>45kg，>90kg，>135kg）
各个取值之间有联系，且是可以互相计算的，比如120kg - 45kg = 90kg，分类之间可以通过数学计算互相转换。这
是有距变量。
然而在对特征进行编码的时候，这三种分类数据都会被我们转换为[0,1,2]，这三个数字在算法看来，是连续且可以
计算的，这三个数字相互不等，有大小，并且有着可以相加相乘的联系。所以算法会把舱门，学历这样的分类特
征，都误会成是体重这样的分类特征。这是说，我们把分类转换成数字的时候，忽略了数字中自带的数学性质，所
以给算法传达了一些不准确的信息，而这会影响我们的建模。
类别OrdinalEncoder可以用来处理有序变量，但对于名义变量，我们只有使用哑变量的方式来处理，才能够尽量
向算法传达最准确的信息：

这样的变化，让算法能够彻底领悟，原来三个取值是没有可计算性质的，是“有你就没有我”的不等概念。在我们的
数据中，性别和舱门，都是这样的名义变量。

2.4 处理连续型特征：二值化与分段

2.4.1 sklearn.preprocessing.Binarizer

大于阈值的值映射为1，而小于或等于阈值的值映射为0。默认阈值为0时，特征中所有的正值都映射到1。
有缺失值报错

2.4.2 preprocessing.KBinsDiscretizer

将连续型变量划分为分类变量的类，能够将连续型变量排序后按顺序分箱后编码。总共包含三个重要参数：

3 feature_selection

3.1 Filter过滤法

3.1.1 方差过滤

建议先使用方差过滤，然后使用互信息法来捕捉相关性

3.1.1.1 VarianceThreshold

无论接下来的特征工程要做什么，都要优先消除方差为0的特征。VarianceThreshold有重要参数threshold，表示方差的阈值，表示舍弃所有方差小于threshold的特征，不填默认为0，即删除所有的记录都相同的特征。

res = VarianceThreshold().fit_transform(x)
1

如果我们知道我们需要多少个特征，方差也可以帮助我们将特征选择一步到位。比如说，我们希望留下一半的特征，那可以设定一个让特征总数减半的方差阈值，只要找到特征方差的中位数，再将这个中位数作为参数threshold的值输入就好了：

#找到特征方差的中位数，再将这个中位数作为参数threshold的值输入
res1 = VarianceThreshold(np.median(x.var().values)).fit_transform(x)
1
2

当特征是二分类时，特征的取值就是伯努利随机变量，这些变量的方差可以计算为：var[X] = p(1-p)
其中X是特征矩阵，p是二分类特征中的一类在这个特征中所占的概率。

#若特征是伯努利随机变量，假设p=0.8，即二分类特征中某种分类占到80%以上的时候删除特征,大多数都是某种变量，因此方差较小
X_bvar = VarianceThreshold(.8 * (1 - .8)).fit_transform(X)
X_bvar.shape
1
2
3

3.1.1.2 方差过滤对模型的影响

最近邻算法KNN，单棵决策树，支持向量机SVM，神经网络，回归算法，都需要遍历特征或升维来进行运算，所以他们本身的运算量就很大，需要的时间就很长，因此方差过滤这样的特征选择对他们来说就尤为重要。但对于不需要遍历特征的算法，比如随机森林，它随机选取特征进行分枝，本身运算就非常快速，因此特征选择对它来说效果平平。这其实很容易理解，无论过滤法如何降低特征的数量，随机森林也只会选取固定数量的特征来建模；而最近邻算法就不同了，特征越少，距离计算的维度就越少，模型明显会随着特征的减少变得轻量。因
此，过滤法的主要对象是：需要遍历特征或升维的算法们，而过滤法的主要目的是：在维持算法表现的前提下，帮助算法们降低计算成本。

过滤法对随机森林无效，却对树模型有效？
从算法原理上来说，传统决策树需要遍历所有特征，计算不纯度后进行分枝，而随机森林却是随机选择特征进
行计算和分枝，因此随机森林的运算更快，过滤法对随机森林无用，对决策树却有用。

在sklearn中，决策树和随机森林都是随机选择特征进行分枝，但决策树在建模过程中随机抽取的特征数目却远远超过随机森林当中每棵树随机抽取的特征数目（比如说对于这个780维的数据，随机森林每棵树只会抽取10-20个特征，而决策树可能会抽取（300~400个特征），因此，过滤法对随机森林无用，却对决策树有用
也因此，在sklearn中，随机森林中的每棵树都比单独的一棵决策树简单得多，高维数据下的随机森林的计算比决策树快很多

对受影响的算法来说，我们可以将方差过滤的影响总结如下：

3.1.1.3 如何选择阈值

一般使用阈值为0或者阈值很小的方差过滤，来为我们优先消除一些明显用不到的特征，然后我们会选择更优的特征选择方法继续削减特征数量。

3.1.2 相关性过滤

希望选出与标签相关且有意义的特征

3.1.2.1 卡方过滤

卡方过滤是专门针对离散型标签（即分类问题）的相关性过滤
使用前需做预处理：不能有负数；卡方检验检测到某个特征中所有的值都相同，会提示我们先进行方差过滤。

#假设我规定我只要300个特征
X_fschi = SelectKBest(chi2, k=300).fit_transform(res1,y)
1
2

3.1.2.2 选取超参数k

通过学习曲线，可知，k越大，模型效果越好，是运行这条曲线的时间同样也是非常地长，接下来我们就来介绍一种更好的选择k的方法：看p值选择k。
卡方检验的本质是推测两组数据之间的差异，其检验的原假设是”两组数据是相互独立的”。卡方检验返回卡方值和P值两个统计量，其中卡方值很难界定有效的范围，而p值，我们一般使用0.01或0.05作为显著性水平，即p值判断的边界，具体我们可以这样来看：

从特征工程的角度，我们希望选取卡方值很大，p值小于0.05的特征，即和标签是相关联的特征。而调用SelectKBest之前，我们可以直接从chi2实例化后的模型中获得各个特征所对应的卡方值和P值。

chivalue, pvalues_chi = chi2(res1,y)
k = chivalue.shape[0]-(pvalues_chi > 0.05).sum()
1
2

3.1.2.2 F检验

用来捕捉每个特征与标签之间的线性关系的过滤方法。它即可以做回归也可以做分类，因此包含feature_selection.f_classif（F检验分类）和feature_selection.f_regression（F检验回归）两个类。
和卡方检验一样，这两个类需要和类SelectKBest连用，并且我们也可以直接通过输出的统计量来判断我们到底要设置一个什么样的K。需要注意的是，F检验在数据服从正态分布时效果会非常稳定，因此如果使用F检验过滤，我们会先将数据转换成服从正态分布的方式。
F检验的本质是寻找两组数据之间的线性关系，其原假设是”数据不存在显著的线性关系“。它返回F值和p值两个统
计量。和卡方过滤一样，我们希望选取p值小于0.05或0.01的特征，这些特征与标签时显著线性相关的，而p值大于0.05或0.01的特征则被我们认为是和标签没有显著线性关系的特征，应该被删除。

from sklearn.feature_selection import f_classif
F,p_f = f_classif(res1,y)
k = F.shape[0]-(p_f > 0.05).sum()
1
2
3

3.1.2.3 互信息法

既可以做回归也可以做分类，并且包含两个类feature_selection.mutual_info_classif（互信息分类）和feature_selection.mutual_info_regression（互信息回归）。互信息法不返回p值或F值类似的统计量，它返回“每个特征与目标之间的互信息量的估计”，这个估计量在[0,1]之间取值，为0则表示两个变量独立，为1则表示两个变量完全相关。

from sklearn.feature_selection import mutual_info_classif as MIC
result = MIC(X_fsvar,y) k = result.shape[0] - sum(result <= 0)
1
2

3.2 Embedded嵌入法

嵌入法是一种让算法自己决定使用哪些特征的方法，即特征选择和算法训练同时进行。在使用嵌入法时，我们先使用某些机器学习的算法和模型进行训练，得到各个特征的权值系数，根据权值系数从大到小选择特征。这些权值系数往往代表了特征对于模型的某种贡献或某种重要性，比如决策树和树的集成模型中的feature_importances_属性，可以列出各个特征对树的建立的贡献，我们就可以基于这种贡献的评估，找出对模型建立最有用的特征。
嵌入式的缺点是权值系数为0的特征对模型丝毫没有作用，但当大量特征都对模型有贡献且贡献不一时，我们就很难去界定一个有效的临界值。这种情况下，模型权值系数就是我们的超参数，我们或许需要学习曲线，或者根据模型本身的某些性质去判断这个超参数的最佳值究竟应该是多少。

3.2.1 feature_selection.SelectFromModel

class sklearn.feature_selection.SelectFromModel (estimator, threshold=None, prefit=False, norm_order=1,max_features=None)
1

SelectFromModel是一个元变换器，可以与任何在拟合后具有coef_，feature_importances_属性或参数中可选惩罚项的评估器一起使用（比如随机森林和树模型就具有属性feature_importances_，逻辑回归就带有l1和l2惩罚项，线性支持向量机也支持l2惩罚项）。
对于有feature_importances_的模型来说，若重要性低于提供的阈值参数，则认为这些特征不重要并被移除。feature_importances_的取值范围是[0,1]，如果设置阈值很小，比如0.001，就可以删除那些对标签预测完全没贡献的特征。如果设置得很接近1，可能只留下没几个特征。

可以使用学习曲线来帮助我们寻找最佳特征值，以随机森林为例：

from sklearn.feature_selection import SelectFromModel
from sklearn.ensemble import RandomForestClassifier as RFC
RFC_ = RFC(n_estimators =10,random_state=0)
X_embedded = SelectFromModel(RFC_,threshold=0.005).fit_transform(X,y) #在这里我只想取出来有限的特征。0.005这个阈值对于有780个特征的数据来说，是非常高的阈值，因为平均每个特征
只能够分到大约0.001的feature_importances_
X_embedded.shape
#模型的维度明显被降低了
#同样的，我们也可以画学习曲线来找最佳阈值
RFC_.fit(X,y).feature_importances_
threshold = np.linspace(0,(RFC_.fit(X,y).feature_importances_).max(),20)
score = []
for i in threshold:
    X_embedded = SelectFromModel(RFC_,threshold=i).fit_transform(X,y)
    once = cross_val_score(RFC_,X_embedded,y,cv=5).mean()
    score.append(once)
plt.plot(threshold,score)
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

和其他调参一样，我们可以在第一条学习曲线后选定一个范围，使用细化的学习曲线来找到最佳值：

score2 = []
for i in np.linspace(0,0.00134,20):
    X_embedded = SelectFromModel(RFC_,threshold=i).fit_transform(X,y)
    once = cross_val_score(RFC_,X_embedded,y,cv=5).mean()
    score2.append(once)
plt.figure(figsize=[20,5])
plt.plot(np.linspace(0,0.00134,20),score2)
plt.xticks(np.linspace(0,0.00134,20))
plt.show()
1
2
3
4
5
6
7
8
9

在嵌入法下，我们很容易就能够实现特征选择的目标：减少计算量，提升模型表现。因此，比起要思考很多统计量的过滤法来说，嵌入法可能是更有效的一种方法。然而，在算法本身很复杂的时候，过滤法的计算远远比嵌入法要快，所以大型数据中，我们还是会优先考虑过滤法。

3.3 Wrapper包装法

包装法也是一个特征选择和算法训练同时进行的方法，与嵌入法十分相似，它也是依赖于算法自身的选择，比如coef_属性或feature_importances_属性来完成特征选择。但不同的是，我们往往使用一个目标函数作为黑盒来帮助我们选取特征，而不是自己输入某个评估指标或统计量的阈值。包装法在初始特征集上训练评估器，并且通过coef_属性或通过feature_importances_属性获得每个特征的重要性。然后，从当前的一组特征中修剪最不重要的特征。在修剪的集合上递归地重复该过程，直到最终到达所需数量的要选择的特征。区别于过滤法和嵌入法的一次训练解决所有问题，包装法要使用特征子集进行多次训练，因此它所需要的计算成本是最高的。
最典型的目标函数是递归特征消除法（Recursive feature elimination, 简写为RFE）。它是一种贪婪的优化算法，旨在找到性能最佳的特征子集。 它反复创建模型，并在每次迭代时保留最佳特征或剔除最差特征，下一次迭代时，它会使用上一次建模中没有被选中的特征来构建下一个模型，直到所有特征都耗尽为止。 然后，它根据自己保留或剔除特征的顺序来对特征进行排名，最终选出一个最佳子集。包装法的效果是所有特征选择方法中最利于提升模型表现的，它可以使用很少的特征达到很优秀的效果。除此之外，在特征数目相同时，包装法和嵌入法的效果能够匹敌，不过它比嵌入法算得更见缓慢，所以也不适用于太大型的数据。相比之下，包装法是最能保证模型效果的特征选择方法。

3.3.1 feature_selection.RFE

class sklearn.feature_selection.RFE (estimator, n_features_to_select=None, step=1, verbose=0)
1

参数estimator是需要填写的实例化后的评估器，n_features_to_select是想要选择的特征个数，step表示每次迭代中希望移除的特征个数。除此之外，RFE类有两个很重要的属性，.support_：返回所有的特征的是否最后被选中的布尔矩阵，以及.ranking_返回特征的按数次迭代中综合重要性的排名。类feature_selection.RFECV会在交叉验证循环中执行RFE以找到最佳数量的特征，增加参数cv，其他用法都和RFE一模一样。

from sklearn.feature_selection import RFE 
RFC_ = RFC(n_estimators =10,random_state=0) 
selector = RFE(RFC_,n_features_to_select=340, step=50).fit(X, y) 
selector.support_.sum() 
selector.ranking_ 
X_wrapper = selector.transform(X) 
cross_val_score(RFC_,X_wrapper,y,cv=5).mean()
1
2
3
4
5
6
7

们也可以对包装法画学习曲线：

score = []
for i in range(1,751,50):
    X_wrapper = RFE(RFC_,n_features_to_select=i, step=50).fit_transform(X,y)
    once = cross_val_score(RFC_,X_wrapper,y,cv=5).mean()
    score.append(once)
plt.figure(figsize=[20,5])
plt.plot(range(1,751,50),score)
plt.xticks(range(1,751,50))
plt.show()
1
2
3
4
5
6
7
8
9

过滤法更快速，但更粗糙。包装法和嵌入法更精确，比较适合具体到算法去调整，但计算量比较大，运行时间长。当数据量很大的时候，优先使用方差过滤和互信息法调整，再上其他特征选择方法。使用逻辑回归时，优先使用嵌入法。使用支持向量机时，优先使用包装法。迷茫的时候，从过滤法走起，看具体数据具体分析。其实特征选择只是特征工程中的第一步