Datawhale 李宏毅机器学习笔记_李宏毅交叉验证

李宏毅机器学习第一章任务

认识机器学习

机器学习自发展以来在最近的时间里取得了非常夸张的热度与学习热情，但我们始终要认识明白的是，什么是机器学习，他与传统的程序设计的区别在哪里，又有何种优势?

机器学习的产生

对于人类和其他生物而言，行为的产生往往可以分为两类，后天以及先天。先天行为往往来自于基因的传承，这种行为往往生下来时生物就具备这种能力。也就是常说的本能，后天行为多来自与外界的熏陶与影响，而生物从外界汲取这种行为并作为固有能力的行为就称作学习

那么机器该如何学习呢？

机器学习的目标

机器学习的目标就是解决上文所提出的问题，也就是建立一个有序的数学模型能够对输入的信息建立出适合的反馈，取代繁复的if结构来减轻人们或者开发者的工作负担

也就是我们在寻找一个满足我们需求的function

机器学习的不同分支

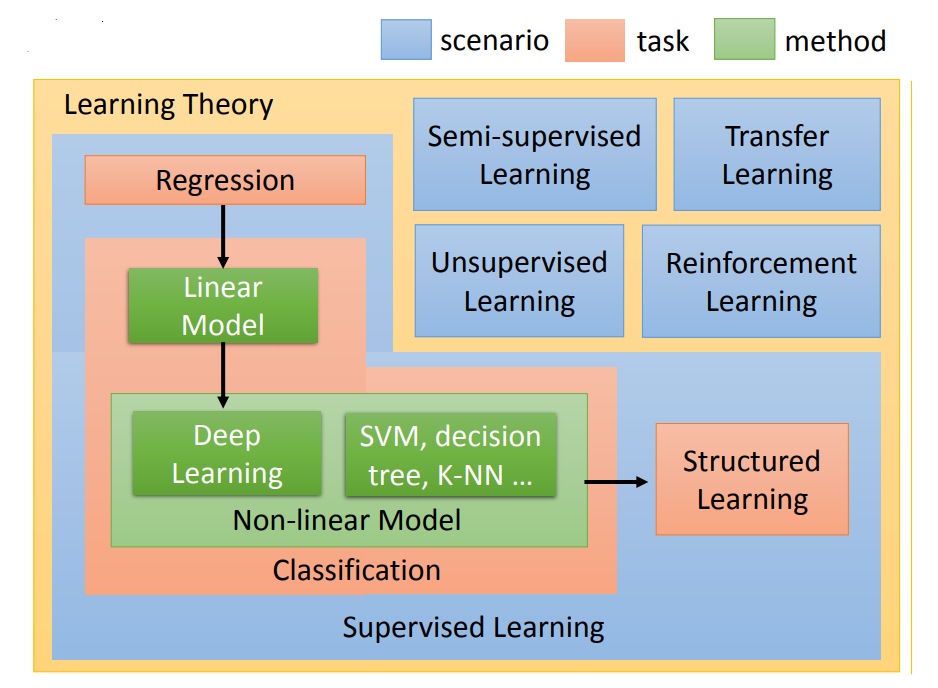
监督学习（supervised Learning）

当我们要处理形如预测股市走向，推测糖尿病病发概率这种数学问题时，往往需要让机器在阅读大量标识好的数据集后才能够得到一个可用而且精准的function

Regression和Classification

Regression和Classification的差别就是我们要机器输出的东西的类型是不一样。在Regression中机器输出的是一个数值，在Classification里面机器输出的是类别。假设Classification问题分成两种，一种叫做二分类输出的是是或否（Yes or No）；另一类叫做多分类（Multi-class），在Multi-class中是让机器做一个选择题，等于是给他数个选项，每个选项都是一个类别，让他从数个类别里选择正确的类别。

在解任务的过程中第一步就是要选择function set，选不同的function set就是选不同的model。Model有很多种，最简单的就是线性模型，但我们会花很多时间在非线性的模型上。在非线性的模型中最耳熟能详的就是Deep learning。

监督学习中的结构化学习（structured learning）

structured learning 中让机器输出的是要有结构性的，举例来说：在语音辨识里面，机器输入是声音讯号，输出是一个句子。句子是要很多词汇拼凑完成。它是一个有结构性的object。或者是说在机器翻译里面你说一句话，你输入中文希望机器翻成英文，它的输出也是有结构性的。或者你今天要做的是人脸辨识，来给机器看张图片，它会知道说最左边是长门，中间是凉宫春日，右边是宝玖瑠。然后机器要把这些东西标出来，这也是一个structure learning问题。

可以总结说，Structured learning 在输入一定的task和label后，要求的输出不仅要在局部上有序，同时全局来看一定也需要成一定的结构与规律

半监督学习（Semi-supervised Learning）

假设你先想让机器鉴别猫狗的不同。你想做一个分类器让它告诉你，图片上是猫还是狗。你有少量的猫和狗的labelled data，但是同时你又有大量的Unlabeled data，但是你没有力气去告诉机器说哪些是猫哪些是狗。在半监督学习的技术中，这些没有label的data，他可能也是对学习有帮助。这个我们之后会讲为什么这些没有label的data对学习会有帮助。

迁移学习（Transfer Learning）

迁移学习的意思是：假设我们要做猫和狗的分类问题，我们也一样，只有少量的有label的data。但是我们现在有大量的data，这些大量的data中可能有label也可能没有label。但是他跟我们现在要考虑的问题是没有什么特别的关系的，我们要分辨的是猫和狗的不同，但是这边有一大堆其他动物的图片还是动画图片（凉宫春日，御坂美琴）你有这一大堆不相干的图片，它到底可以带来什么帮助。这个就是迁移学习要讲的问题。

无监督学习（Unsupervised Learning）

在传统的监督学习中，我们往往在指定完机器要完成的task之后还要指定一部分的label值供机器进行进一步的学习参考，而无监督学习放弃了指定label值：假设我们今天带机器去动物园让它看一大堆的动物，它能不能够在看了一大堆动物以后，它就学会自己创造一些动物。那这个都是真实例子。仔细看了大量的动物以后，它就可以自己的画一些狗出来。有眼睛长在身上的狗、还有乳牛狗等等。

强化学习（reinforcement learning）

我们若将强化学习和监督学习进行比较时，在监督学习中我们会告诉机器正确答案是什么。若现在我们要用监督学习的方法来训练一个聊天机器人，你的训练方式会是：你就告诉机器，现在使用者说了hello，你就说hi，现在使用者说了byebye ，你就说good bye。所以机器有一个人当他家教在他旁边手把手的教他每件事情，这就是监督学习。

reinforcement learning是什么呢？在reinforcement learning里面，我们没有告诉机器正确的答案是什么，机器所拥有的只有一个分数，就是他做的好还是不好。若我们现在要用reinforcement learning方法来训练一个聊天机器人的话，他训练的方法会是这样：你就把机器发到线下，让他的和面进来的客人对话，然后想了半天以后呢，最后仍旧勃然大怒把电话挂掉了。那机器就学到一件事情就是刚才做错了。但是他不知道哪边错了，它就要回去自己想道理，是一开始就不应该打招呼吗？还是中间不应该在骂脏话了之类。它不知道，也没有人告诉它哪里做的不好，它要回去反省检讨哪一步做的不好。机器要在reinforcement learning的情况下学习，机器是非常intelligence的。 reinforcement learning也是比较符合我们人类真正的学习的情景，这是你在学校里面的学习老师会告诉你答案，但在真实社会中没人回告诉你正确答案。你只知道你做得好还是做得不好，如果机器可以做到reinforcement learning，那确实是比较intelligence。

李宏毅机器学习第二章任务

回归定义和应用例子

Regression 就是找到一个函数function，通过输入特征 x，输出一个数值 Scalar。

常见应用

• 股市预测（Stock market forecast）

  • 输入：过去10年股票的变动、新闻咨询、公司并购咨询等
  • 输出：预测股市明天的平均值

• 自动驾驶（Self-driving Car）

  • 输入：无人车上的各个sensor的数据，例如路况、测出的车距等
  • 输出：方向盘的角度

创建一个模型的具体步骤（线性模型）

• step1：模型假设，选择模型框架（线性模型）
• step2：模型评估，如何判断众多模型的好坏（损失函数）
• step3：模型优化，如何筛选最优的模型（梯度下降）

一元线性模型（y=b+wx）

一元线性模型往往在生活中的推测中适用性较差，应用场景有限，因为其本身无法很好的处理多个异常点

多元线性模型

在实际应用中，function内传入的参数往往是多样的，这时一元的线性模型已经无法满足需要

所以我们假设 线性模型 Linear model ：y=b+∑wi*xi

• xi：就是各种特征(fetrure)
• wi：各个特征的权重
• b：偏移量

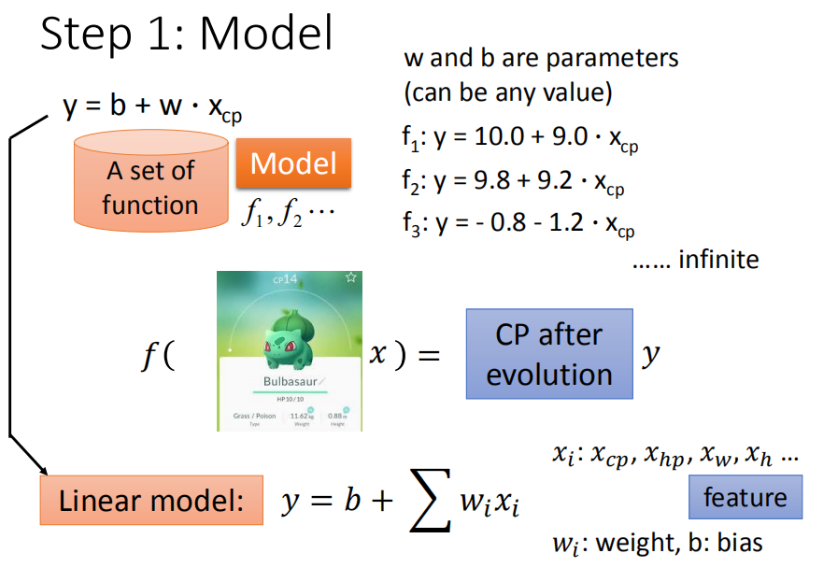
以宝可梦为例，在处理推测宝可梦战斗进化问题时，传入的function往往需要多个参数，不同参数有不同的权重

模型评估（损失函数）

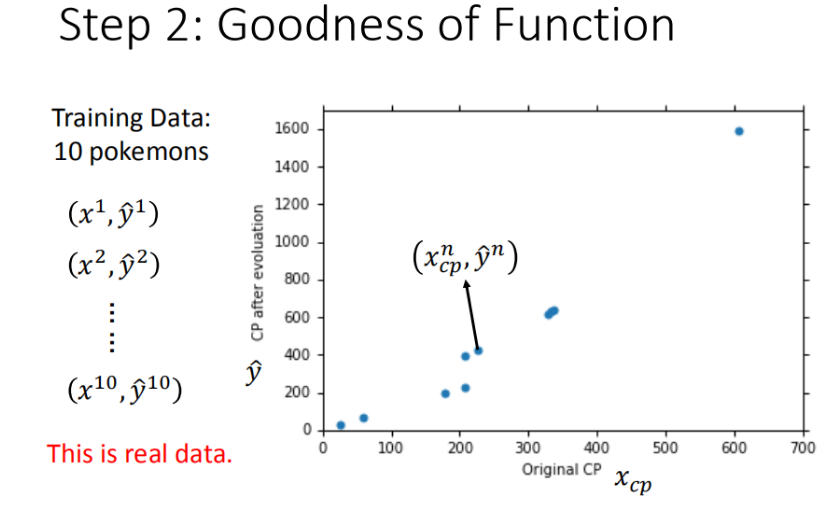
将已知的10只宝可梦的进化数据放在图内观察，我们此时要做的就是描绘出预测出的function图像，观察其对于途中已知点的拟合度，如何判别这个标准呢？我们就需要引入一个函数（损失函数）。

上式即为均方误差损失函数（MSE）

在回归问题中，均方误差损失函数用于度量样本点到回归曲线的距离，通过最小化平方损失使样本点可以更好地拟合回归曲线。均方误差损失函数（MSE）的值越小，表示预测模型描述的样本数据具有越好的精确度。由于无参数、计算成本低和具有明确物理意义等优点，MSE已成为一种优秀的距离度量方法。尽管MSE在图像和语音处理方面表现较弱，但它仍是评价信号质量的标准，在回归问题中，MSE常被作为模型的经验损失或算法的性能指标。

**L2损失又被称为欧氏距离，**是一种常用的距离度量方法，通常用于度量数据点之间的相似度。由于L2损失具有凸性和可微性，且在独立、同分布的高斯噪声情况下，它能提供最大似然估计，使得它成为回归问题、模式识别、图像处理中最常使用的损失函数。

L1损失又称为曼哈顿距离，表示残差的绝对值之和。L1损失函数对离群点有很好的鲁棒性，但它在残差为零处却不可导。另一个缺点是更新的梯度始终相同，也就是说，即使很小的损失值，梯度也很大，这样不利于模型的收敛。针对它的收敛问题，一般的解决办法是在优化算法中使用变化的学习率，在损失接近最小值时降低学习率。

在使用MSE的情况下，我们将 w, b 在二维坐标图中展示，如图所示：

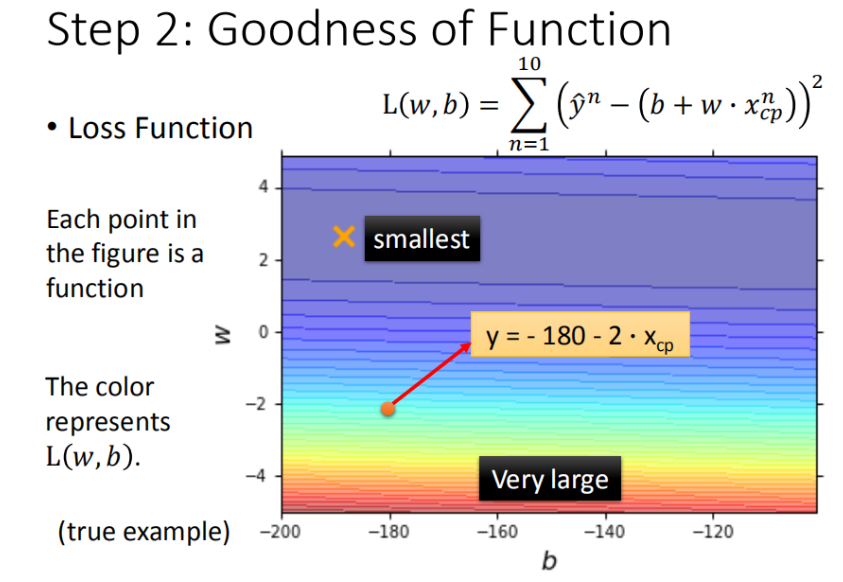
最佳模型（梯度下降）

如何筛选最优的模型（参数w，b）

已知损失函数MSE，我们需要找到最符合实际需要的参数w，b

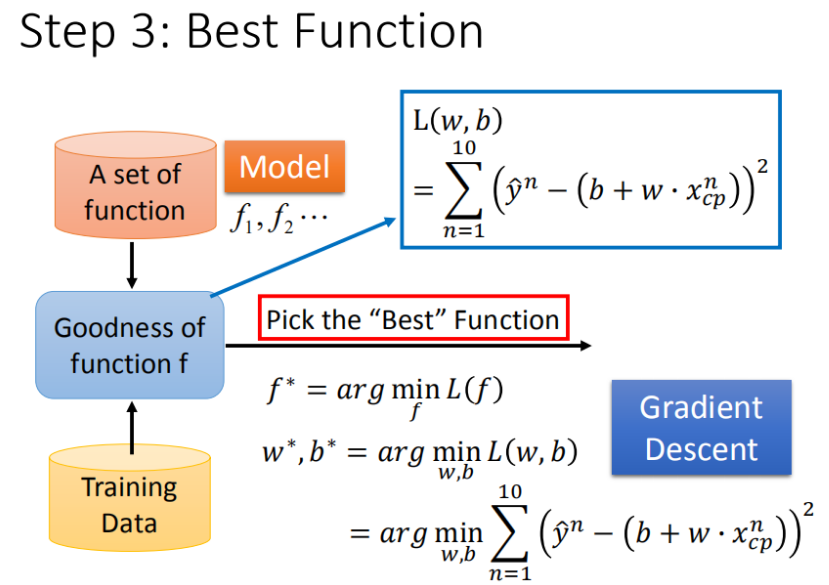
如何找寻呢？

我们可以以一个参数为例：

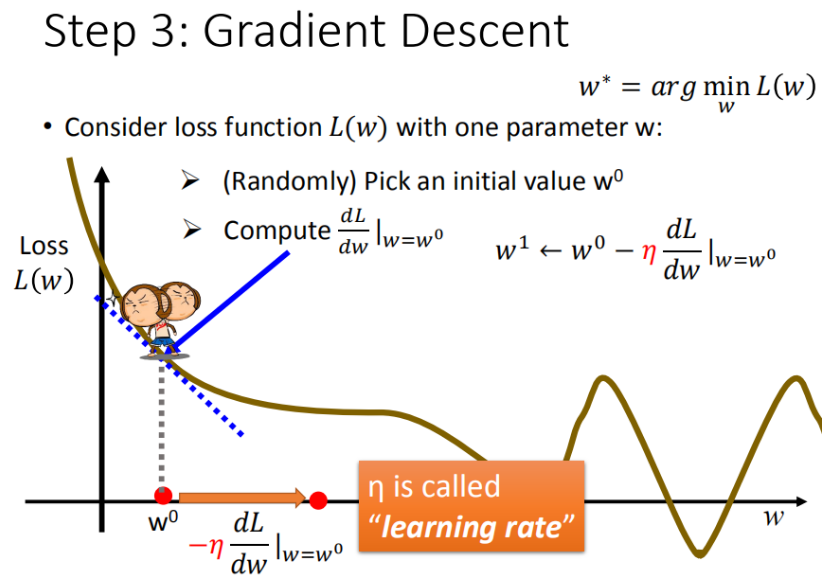
首先在这里引入一个概念 学习率 ：移动的步长，如图7中 *η*

• 步骤1：随机选取一个 w
• 步骤2：计算微分，也就是当前的斜率，根据斜率来判定移动的方向
  • 大于0向右移动（增加w）
  • 小于0向左移动（减少w）
• 步骤3：根据学习率移动
• 重复步骤2和步骤3，直到找到最低点

通过过程的不断迭代，最终能够找出问题的局部最优解

但是同时问题也来了：为什么此时的局部最优解是我们想要的全局最优解呢？

在MSE算法内，对该函数求微分，发现其为一个凹函数

而凹函数在除去**等于0（Stuck at saddle point）和 趋近于0（Very slow at the plateau）**时都能够满足我们的需要。

如何验证训练好的模型的好坏

常见的验证方法即为画图观察法

我们可以将训练好的数据与真实数据对比，观察其拟合曲线与数据的贴合度

拟合情况往往有三种情况

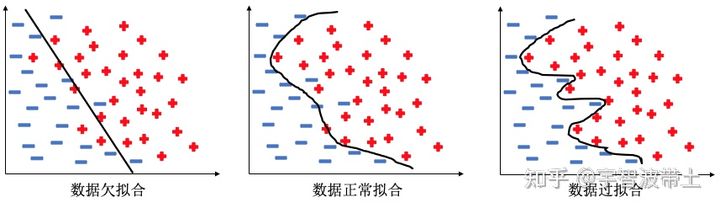
当我们在做数据的拟合时，如果采用低次的模型拟合，往往会出现拟合不够，无法完成指定任务的情况，而当使用过高次的数据拟合时，数据往往在训练集中取得较好成绩，而在测试集中表现过差，原因就在于发生了过拟合现象，模型过于敏感而收录了太多噪声。

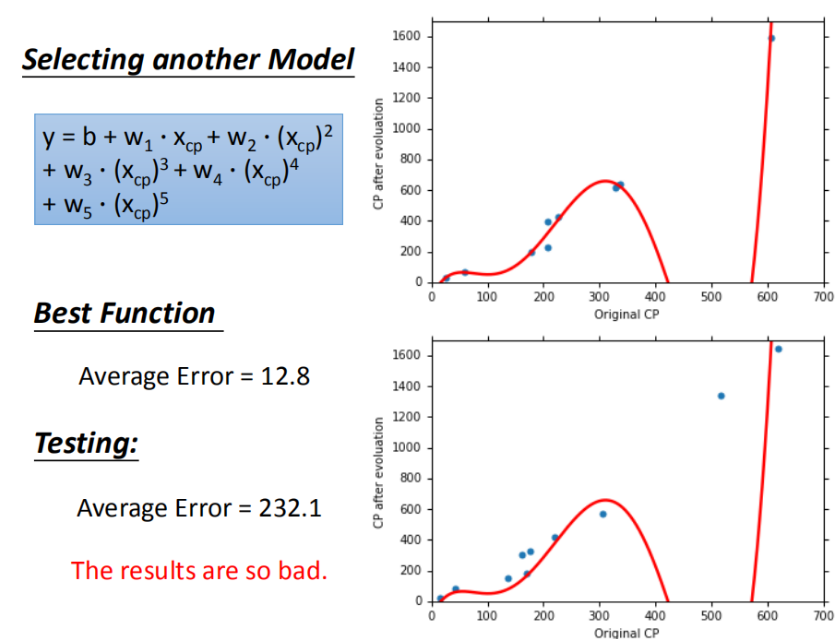
步骤优化

输入更多Pokemons数据，相同的起始CP值，但进化后的CP差距竟然是2倍。如图21，其实将Pokemons种类通过颜色区分，就会发现Pokemons种类是隐藏得比较深得特征，不同Pokemons种类影响了进化后的CP值的结果。

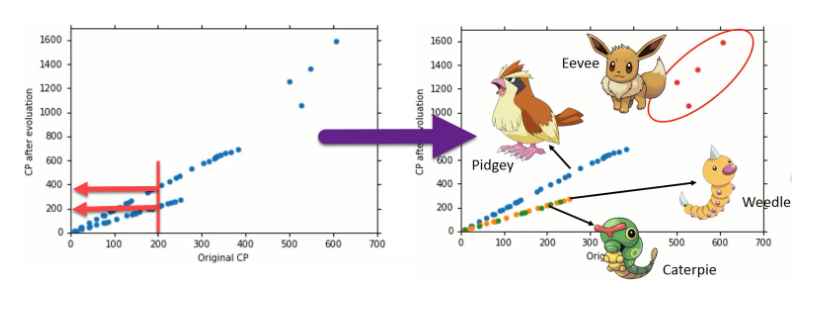
而在数据处理的部分中，往往我们要对这些隐藏特征进行提前处理，来确保在训练中不会错过这些信息

常见的优化思路

2个input的四个线性模型合并到一个模型中

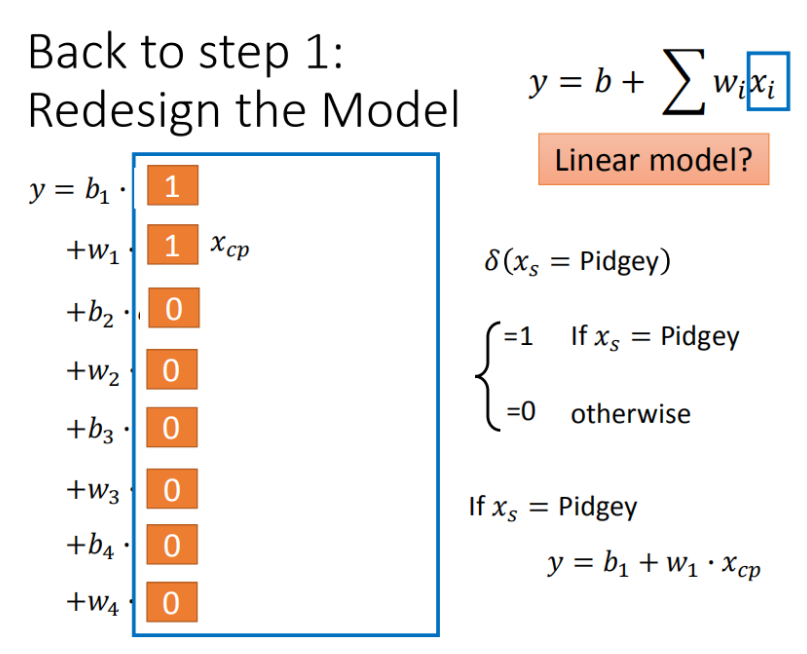
根据另一个参数xs来决定一部分系数

如果希望模型更强大更好（添加多个参数，更多input）

但需要注意的是，添加参数时要对参数进行筛选，防止加入噪声

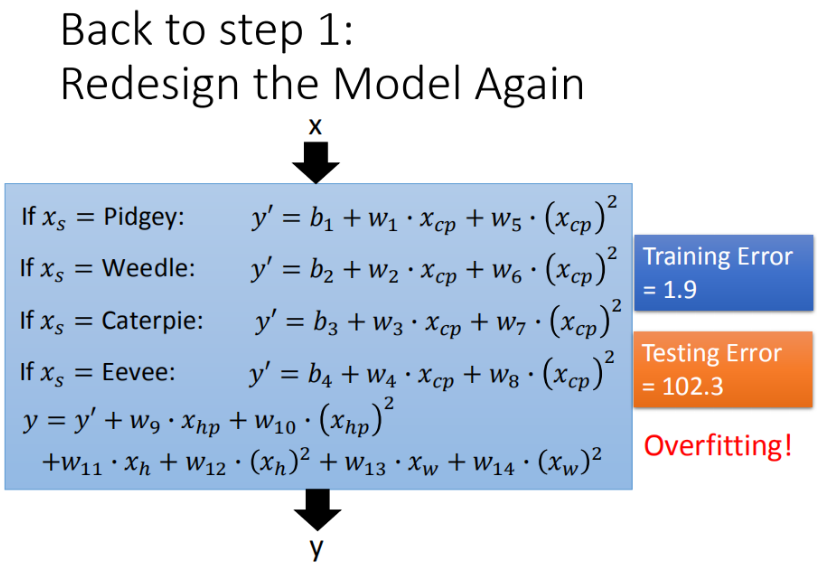
加入正则化

更多特征，但是权重 ww 可能会使某些特征权值过高，仍旧导致overfitting，所以加入正则化

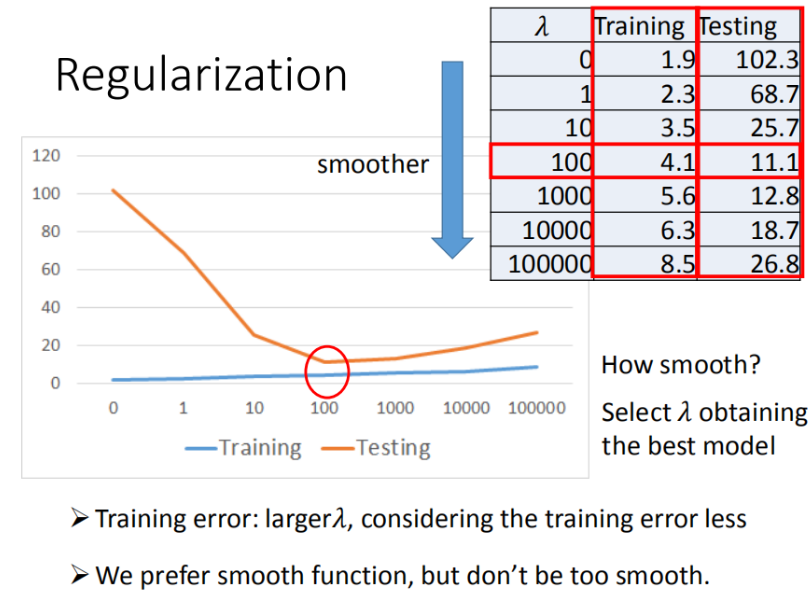
总结

• Pokemon ：原始的CP值极大程度的决定了进化后的CP值，但可能还有其他的一些因素。
• Gradient descent ：梯度下降的做法；后面会讲到它的理论依据和要点。
• Overfitting和Regularization ：过拟合和正则化，主要介绍了表象；后面会讲到更多这方面的理论

李宏毅机器学习第三章任务

Error的来源

在回顾上一章时我们讨论了机器学习中可能会遇到的一些影响结果的情况，如何来评判这种Error呢？

常见模型的主要Error来源主要有两个，分别为bios和variance

即Error = Bias + Variance

Bias

Bias是 “用所有可能的训练数据集训练出的所有模型的输出的 平均值 ” 与 “真实模型”的输出值之间的差异

Error反映的是整个模型的准确度，Bias反映的是模型在样本上的输出与真实值之间的误差，即模型本身的精准度

在刚开始训练时由于训练量比较小，bios数值还比较大，因为它本身在不停地接近真实模型所反应的数值，而在确保训练数据准确性的情况下，这个数值会随着训练量的增大会无限下降，

variance

假设我们现在有一组训练数据，需要训练一个模型（基于梯度的学习，不包括最近邻等方法）。在训练过程的最初，bias很大，因为我们的模型还没有来得及开始学习，也就是与“真实模型”差距很大。然而此时variance却很小，因为 训练数据集（training data）还没有来得及对模型产生影响 ，所以此时将模型应用于“不同的”训练数据集也不会有太大差异。

而当数据训练量不断扩大时，各训练数据集之间的差异就开始发挥作用，

因为我们除了学习到关于真实模型的信息，还学到了 许多具体的，只针对我们使用的训练集 （真实数据的子集）的信息。而 不同的可能训练数据集（真实数据的子集）之间的某些特征和噪声是不一致的 ，这就导致了我们的模型在很多其他的数据集上就无法获得很好的效果，也就是所谓的overfitting。

估测Error

在实际情况中我们往往是不清楚我们想要的那个真实的function，所以我们只能收集大量数据来训练接近我们想要的那个function。

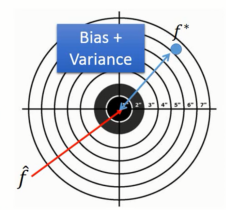
这个过程就像打靶，f^就是我们的靶心，f∗ 就是我们投掷的结果。如上图所示，f^ 与f∗ 之间蓝色部分的差距就是偏差和方差导致的。

估测变量x的偏差和方差

评估x的偏差

假设 xx 的平均值是 \muμ，方差为 \sigma^2σ2

评估平均值要怎么做呢？

• 首先拿到 NN 个样本点：{x^1,x2,···,x^N}{x1,x2**,⋅⋅⋅,xN**}
• 计算平均值 mm, 得到 m=\frac{1}{N}\sum_n x^n \neq \mum=N1∑n****xn=μ

估测变量x的方差

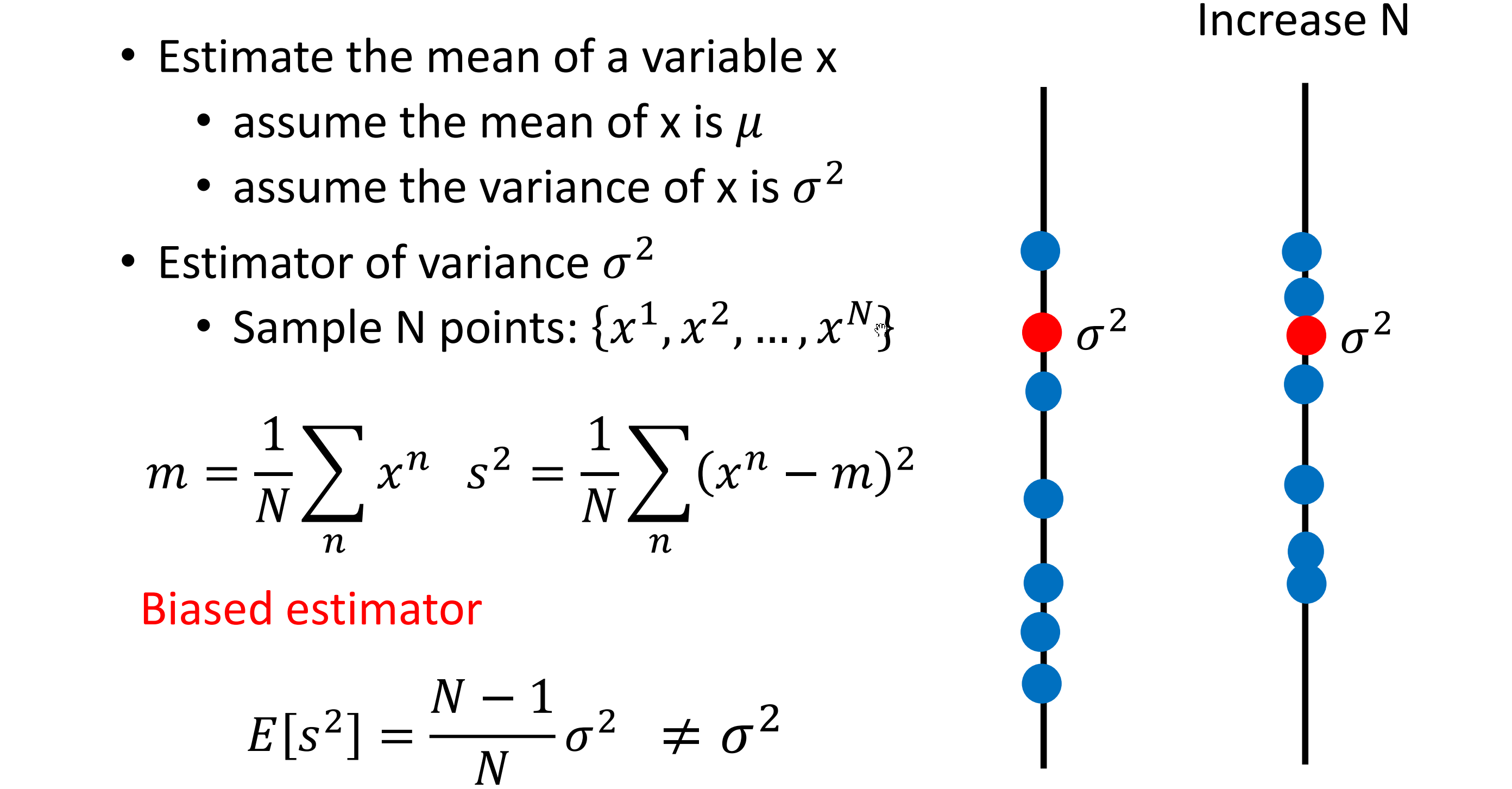
为什么会有很多的模型?

这里以笔者最熟悉的自动驾驶模型做介绍

在采集数据时，在不同场景，不同环境下的采集效果不同，同一个场景，多次采集时得到的数据依然存在偏差，所以对这些数据进行训练时的model是不一样的，而最终我们的模型会受到所有训练结果的干扰

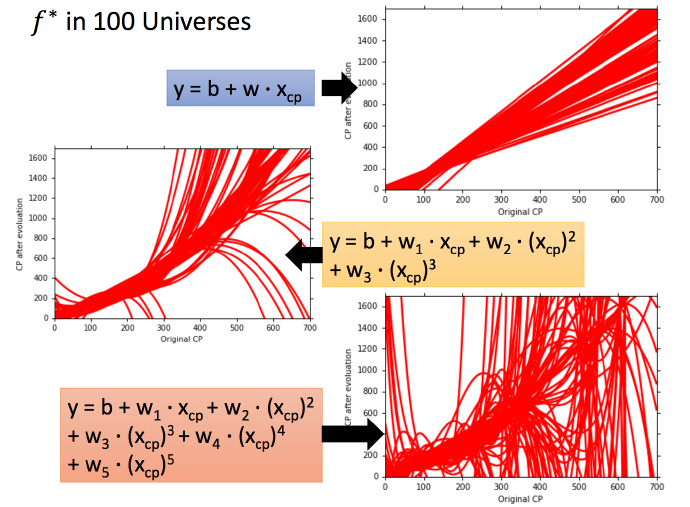
考虑不同模型的方差

一次模型的方差就比较小的，也就是是比较集中，离散程度较小。而5次模型的方差就比较大，同理散布比较广，离散程度较大。

所以用比较简单的模型，方差是比较小的（就像射击的时候每次的时候，每次射击的设置都集中在一个比较小的区域内）。如果用了复杂的模型，方差就很大，散布比较开。

这也是因为简单的模型受到不同训练集的影响是比较小的。

考虑不同模型的偏差

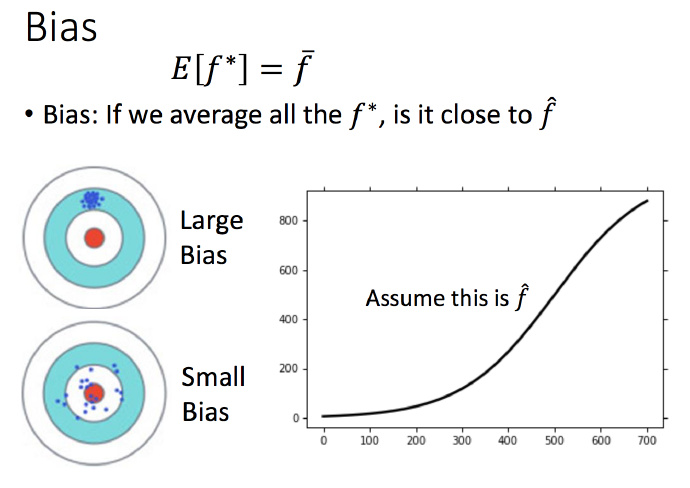
结果可视化，一次平均的fˉ 没有5次的好，虽然5次的整体结果离散程度很高。

一次模型的偏差比较大，而复杂的5次模型，偏差就比较小。

直观的解释：简单的模型函数集的space比较小，所以可能space里面就没有包含靶心，肯定射不中。而复杂的模型函数集的space比较大，可能就包含的靶心，只是没有办法找到确切的靶心在哪，但足够多的，就可能得到真正的 f¯

怎么判断？

关于拟合的三种情况在上一章已经阐述，这一章不再过多介绍

模型选择

现在在偏差和方差之间就需要一个权衡
想选择的模型，可以平衡偏差和方差产生的错误，使得总错误最小
但是下面这件事最好不要做：

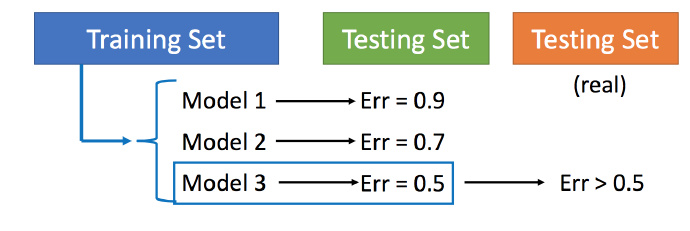
用训练集训练不同的模型，然后在测试集上比较错误，模型3的错误比较小，就认为模型3好。但实际上这只是你手上的测试集，真正完整的测试集并没有。比如在已有的测试集上错误是0.5，但有条件收集到更多的测试集后通常得到的错误都是大于0.5的。

常见的划分训练集的方法

留出法

（1）将数据集划分为互斥的两个部分，一部分是训练集，一部分是测试集

（2）划分时要尽量保证训练集和测试集数据分布的一致性，例如在分类样本中有1000个正样本，100个负样本，那么训练集和测试集中的正负样本比例也要基本遵循10：1这个比例

（3）为了保证划分结果的随机性，可以将数据集多次随机划分，然后对多次划分结果取平均值

（4）训练集和测试集的划分比例没有固定的值，通常将大约2/3~4/5的样本用于训练，最常见的训练集测试集比例有7：3或8：2

交叉验证法

（1） 先将数据集划分为k个大小相似的互斥子集，每个子集尽可能保持数据分布的一致性

（2） 然后每次选k-1个子集一组作为训练集，剩下一个子集作为测试集，共有k种分发得到k组训练集和测试集

（3） 进行k此训练和测试，对结果取平均值

交叉验证法评估结果的稳定性和保真性在很大程度上取决于k的取值，为了强调这一点，通常把交叉验证法称为”k折交叉验证”（k-fold cross validation），k通常取10—10折交叉验证。

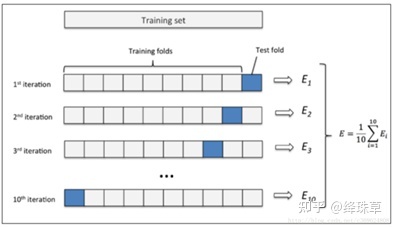
交叉验证的好处就是从有限的数据中尽可能挖掘多的信息，从各种角度去学习我们现有的有限的数据，避免出现局部的极值。缺点就是，当数据集比较大时，训练模型的开销较大

自助法

当样本数量比较少时，为了充分利用样本数据，可采取自助法

（1） 每次随机从数据集（有m个样本）抽取一个样本，然后再放回（也就是说可能被重复抽出），m次后得到有m个样本的数据集，将其作为训练集

（2） 通过概率计算，经过m次抽样后会有约1/3的样本，始终不会被抽到，这部分数据可以用来测试

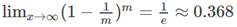
自助法产生的测试集改变了初始数据集的分布，这会引入误差，因此在数据量足够时，采用留出法和交叉验证法较好

李宏毅机器学习第三章任务

什么是梯度下降法？

Review: 梯度下降法

在回归问题中，为了找到model的最合适的参数以此来找到最好的function，我们往往需要优化原有的function参数，也就是要不断的减小Loss函数。

为了解决这个问题，我们采用梯度下降法

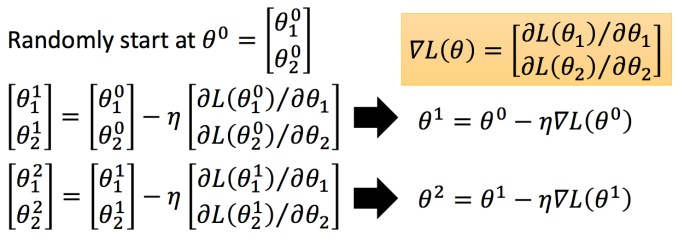
以多参数距离，分别对两个参数微分后使得函数向着减小的方向移动。

分别计算初始点处，两个参数对 L 的偏微分，然后 θ0 减掉 η 乘上偏微分的值，得到一组新的参数。同理反复进行这样的计算。黄色部分为简洁的写法，\triangledown L(\theta)▽L(θ)** 即为梯度。

优化梯度下降的方法

Tips 1：调整学习率（Learning Rate）

选择合适的学习率

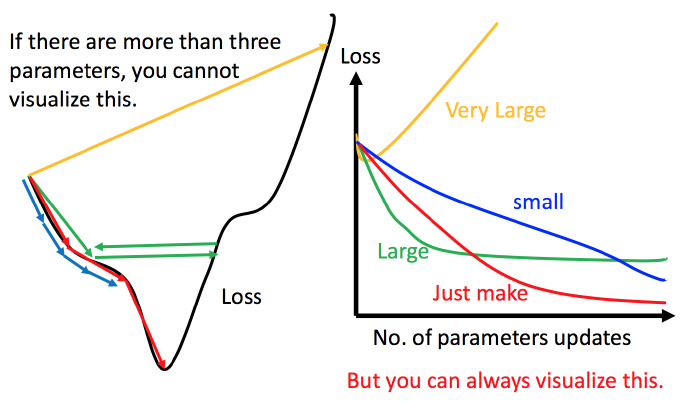
上图左边黑色为损失函数的曲线，假设从左边最高点开始，如果学习率调整的刚刚好，比如红色的线，就能顺利找到最低点。如果学习率调整的太小，比如蓝色的线，就会走的太慢，虽然这种情况给足够多的时间也可以找到最低点，实际情况可能会等不及出结果。如果 学习率调整的有点大，比如绿色的线，就会在上面震荡，走不下去，永远无法到达最低点。还有可能非常大，比如黄色的线，直接就飞出去了，更新参数的时候只会发现损失函数越更新越大。

因此在实际训练过程中选择合适的Learning Rate以及合适的epoch非常重要

自适应学习率

举一个简单的思想：随着次数的增加，通过一些因子来减少学习率

• 通常刚开始，初始点会距离最低点比较远，所以使用大一点的学习率
• update好几次参数之后呢，比较靠近最低点了，此时减少学习率

学习率不能是一个值通用所有特征，不同的参数需要不同的学习率

Adagrad算法

对于经典的SGD优化方法，参数θ的更新为：

再来看AdaGrad算法表示为：

其中，r为梯度累积变量，r的初始值为0。ε为全局学习率，需要自己设置。δ为小常数。

dagrad算法分析

（1）从AdaGrad算法中可以看出，随着算法不断迭代，r会越来越大，整体的学习率会越来越小。所以，一般来说AdaGrad算法一开始是激励收敛，到了后面就慢慢变成惩罚收敛，速度越来越慢。

（2）在SGD中，随着梯度
的增大，我们的学习步长应该是增大的。但是在AdaGrad中，随着梯度g的增大，我们的r也在逐渐的增大，且在梯度更新时r在分母上，也就是整个学习率是减少的，这是为什么呢？

这是因为随着更新次数的增大，我们希望学习率越来越慢。因为我们认为在学习率的最初阶段，我们距离损失函数最优解还很远，随着更新次数的增加，越来越接近最优解，所以学习率也随之变慢。

（3）经验上已经发现，对于训练深度神经网络模型而言，从训练开始时积累梯度平方会导致有效学习率过早和过量的减小。AdaGrade在某些深度学习模型上效果不错，但不是全部。

AdaGrad算法存在的矛盾

在 Adagrad 中，当梯度越大的时候，步伐应该越大，但下面分母又导致当梯度越大的时候，步伐会越小。

最好的步伐应该是：不止和一次微分成正比，还和二次微分成反比。最好的step应该考虑到二次微分：

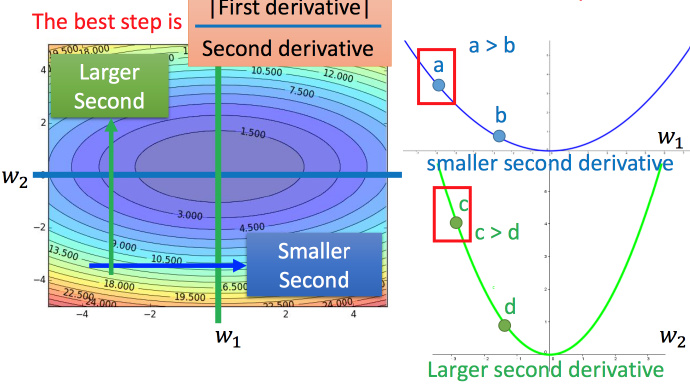
Adagrad算法进一步的解释

再回到之前的 Adagrad

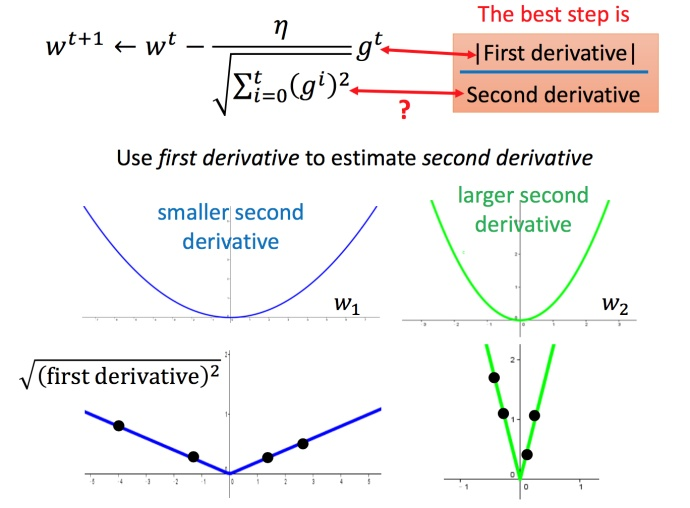
这里的分母就是在代价尽量小的情况下模拟二次微分

Tips 2：随机梯度下降法

随机梯度下降法更快：

损失函数不需要处理训练集所有的数据，选取一个例子 x^n

此时不需要像之前那样对所有的数据进行处理，只需要计算某一个例子的损失函数Ln，就可以赶紧update 梯度。

常规梯度下降法走一步要处理到所有二十个例子，但随机算法此时已经走了二十步（每处理一个例子就更新）

Tips 3: 特征缩放

为什么要进行特征缩放？

1. 统一特征的权重&提升模型准确性

如果某个特征的取值范围比其他特征大很多，那么数值计算（比如说计算欧式距离）就受该特征的主要支配。但实际上并不一定是这个特征最重要，通常需要把每个特征看成同等重要。归一化/标准化数据可以使不同维度的特征放在一起进行比较，可以大大提高模型的准确性。

2. 提升梯度下降法的收敛速度

在使用梯度下降法求解最优化问题时， 归一化/标准化数据后可以加快梯度下降的求解速度。

具体使用哪种方法进行特征缩放？

在需要使用距离来度量相似性的算法中，或者使用PCA技术进行降维的时候，通常使用 标准化（standardization或均值归一化（mean normalization）比较好，但如果数据分布不是正态分布或者标准差非常小，以及需要把数据固定在 [0, 1] 范围内，那么使用 最大最小值归一化（min-max normalization） 比较好（min-max 常用于归一化图像的灰度值）。但是min-max比较容易受异常值的影响，如果数据集包含较多的异常值，可以考虑使用 稳键归一化（robust normalization） 。对于已经中心化的数据或稀疏数据的缩放，比较推荐使用 最大绝对值归一化（max abs normalization ） ，因为它会保住数据中的０元素，不会破坏数据的稀疏性（sparsity）。

哪些机器学习模型必须进行特征缩放？

通过梯度下降法求解的模型需要进行特征缩放，这包括线性回归（Linear Regression）、逻辑回归（Logistic Regression）、感知机（Perceptron）、支持向量机（SVM）、神经网络（Neural Network）等模型。此外，近邻法（KNN），K均值聚类（K-Means）等需要根据数据间的距离来划分数据的算法也需要进行特征缩放。主成分分析（PCA），线性判别分析（LDA）等需要计算特征的方差的算法也会受到特征缩放的影响。

决策树（Decision Tree），随机森林（Random Forest）等基于树的分类模型不需要进行特征缩放，因为特征缩放不会改变样本在特征上的信息增益。

进行特征缩放的注意事项：

需要先把数据拆分成训练集与验证集，在训练集上计算出需要的数值（如均值和标准值），对训练集数据做标准化/归一化处理（不要在整个数据集上做标准化/归一化处理，因为这样会将验证集的信息带入到训练集中，这是一个非常容易犯的错误），然后再用之前计算出的数据（如均值和标准值）对验证集数据做相同的标准化/归一化处理。

梯度下降的理论基础

当用梯度下降解决问题：

每次更新参数 θ，都得到一个新的 θ，它都使得损失函数更小。即：

L(θ0)>L(θ1)>L(θ2)>⋅⋅⋅

上述结论正确吗？

结论是不正确的。。。

数学理论

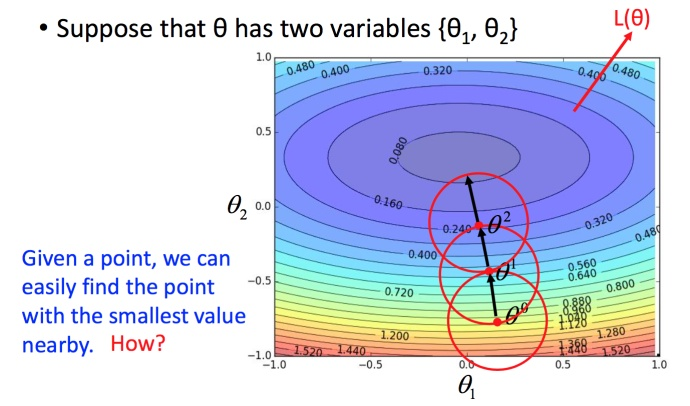
比如在 θ0 处，可以在一个小范围的圆圈内找到损失函数细小的 θ1，不断的这样去寻找。

接下来就是如果在小圆圈内快速的找到最小值？

泰勒展开式

先介绍一下泰勒展开式

定义

若 h(x) 在 x=x0 点的某个领域内有无限阶导数（即无限可微分，infinitely differentiable），那么在此领域内有：

多变量泰勒展开即为对多变量求微分的相仿形式

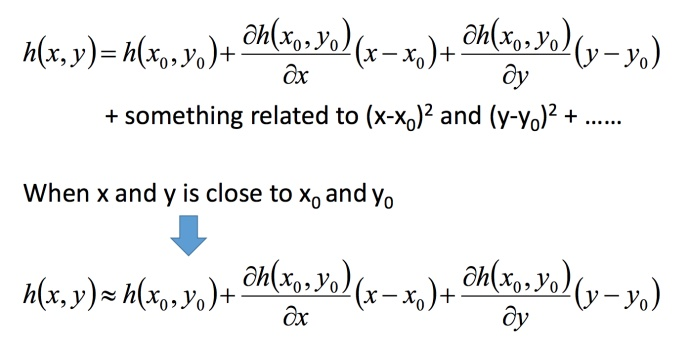
利用泰勒展开式简化

回到之前如何快速在圆圈内找到最小值。基于泰勒展开式，在 (a,b) 点的红色圆圈范围内，可以将损失函数用泰勒展开式进行简化：

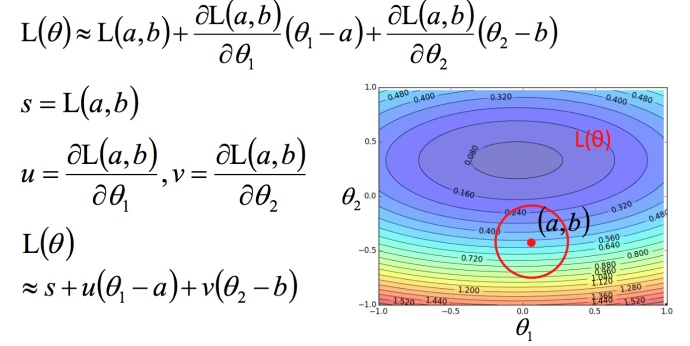
将问题进而简化为下图：

不考虑s的话，可以看出剩下的部分就是两个向量(△θ1,△θ2) 和 (u,v) 的内积，那怎样让它最小，就是和向量 (u,v) 方向相反的向量。

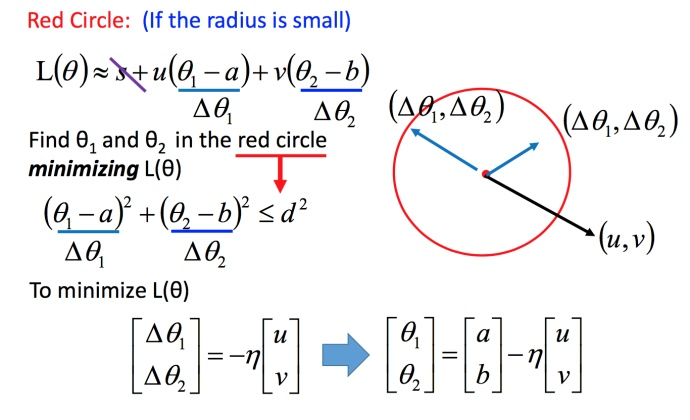
然后将u和v带入。

发现最后的式子就是梯度下降的式子。但这里用这种方法找到这个式子有个前提，泰勒展开式给的损失函数的估算值是要足够精确的，而这需要红色的圈圈足够小（也就是学习率足够小）来保证。所以理论上每次更新参数都想要损失函数减小的话，即保证式1-2 成立的话，就需要学习率足够足够小才可以。

所以实际中，当更新参数的时候，如果学习率没有设好，是有可能式1-2是不成立的，所以导致做梯度下降的时候，损失函数没有越来越小。

式1-2只考虑了泰勒展开式的一次项，如果考虑到二次项（比如牛顿法），在实际中不是特别好，会涉及到二次微分等，多很多的运算，性价比不好。

梯度下降的限制

这些内容在前面已经阐述过，此处不再赘述。

李宏毅机器学习第四章任务

深度学习的发展趋势

回顾一下deep learning的历史：

• 1958: Perceptron (linear model)
• 1969: Perceptron has limitation
• 1980s: Multi-layer perceptron
  • Do not have significant difference from DNN today
• 1986: Backpropagation
  • Usually more than 3 hidden layers is not helpful
• 1989: 1 hidden layer is “good enough”, why deep?
• 2006: RBM initialization (breakthrough)
• 2009: GPU
• 2011: Start to be popular in speech recognition
• 2012: win ILSVRC image competition
  感知机（Perceptron）非常像我们的逻辑回归（Logistics Regression）只不过是没有 sigmoid激活函数。09年的GPU的发展是很关键的，使用GPU矩阵运算节省了很多的时间。

激活函数

激活函数是向神经网络中引入非线性因素，通过激活函数神经网络就可以拟合各种曲线。激活函数主要分为饱和激活函数（Saturated Neurons）和非饱和函数（One-sided Saturations） 。Sigmoid和Tanh是饱和激活函数，而ReLU以及其变种为非饱和激活函数。非饱和激活函数主要有如下优势：

1.非饱和激活函数可以解决梯度消失问题。

2.非饱和激活函数可以加速收敛。

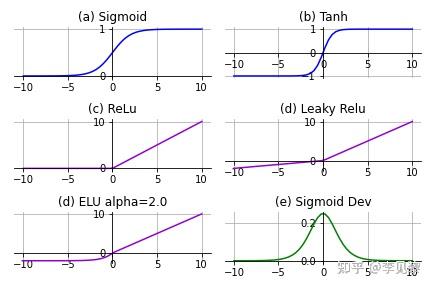
梯度消失(Vanishing Gradients)

Sigmoid的函数图像和Sigmoid的梯度函数图像分别为(a)、(e)，从图像可以看出，函数两个边缘的梯度约为0，梯度的取值范围为(0,0.25)。求解方程为：

1. Sigmoid极容易导致梯度消失问题。饱和神经元会使得梯度消失问题雪上加霜，假设神经元输入Sigmoid的值特别大或特别小，对应的梯度约等于0，即使从上一步传导来的梯度较大，该神经元权重(w)和偏置(bias)的梯度也会趋近于0，导致参数无法得到有效更新。
2. 计算费时。 在神经网络训练中，常常要计算Sigmid的值进行幂计算会导致耗时增加。
3. Sigmoid函数不是关于原点中心对称的（zero-centered)。

Tanh激活函数解决了原点中心对称问题。

深度学习的三个步骤

• Step1：神经网络（Neural network）
• Step2：模型评估（Goodness of function）
• Step3：选择最优函数（Pick best function）

Step1：神经网络

神经网络（Neural network）里面的节点，类似我们的神经元。

神经网络也可以有很多不同的连接方式，这样就会产生不同的结构（structure）在这个神经网络里面，我们有很多逻辑回归函数，其中每个逻辑回归都有自己的权重和自己的偏差，这些权重和偏差就是参数。
那这些神经元都是通过什么方式连接的呢？其实连接方式都是你手动去设计的。

完全连接前馈神经网络

概念：前馈（feedforward）也可以称为前向，从信号流向来理解就是输入信号进入网络后，信号流动是单向的，即信号从前一层流向后一层，一直到输出层，其中任意两层之间的连接并没有反馈（feedback），亦即信号没有从后一层又返回到前一层。

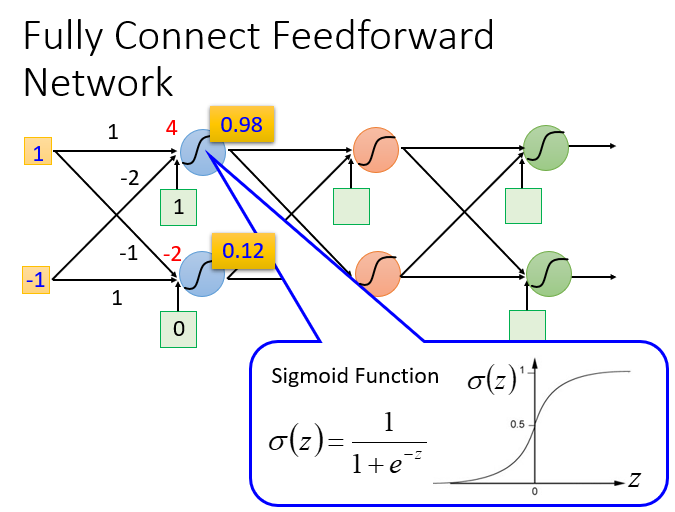
全链接和前馈的理解

• 输入层（Input Layer）：1层
• 隐藏层（Hidden Layer）：N层
• 输出层（Output Layer）：1层

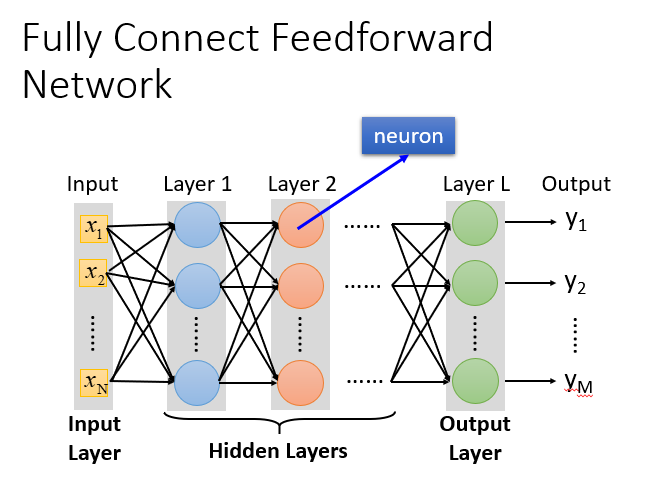
• 为什么叫全链接呢？
  • 因为layer1与layer2之间两两都有连接，所以叫做Fully Connect；
• 为什么叫前馈呢？
  • 因为现在传递的方向是由后往前传，所以叫做Feedforward。

深度的理解

那什么叫做Deep呢？Deep = Many hidden layer。那到底可以有几层呢？这个就很难说了，以下是老师举出的一些比较深的神经网络的例子

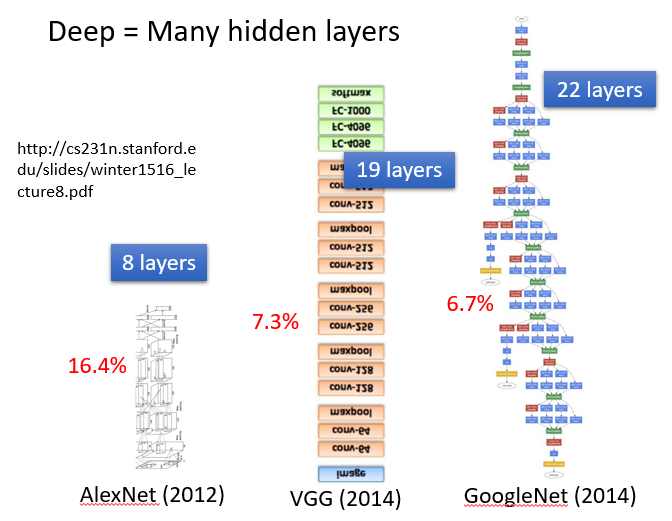
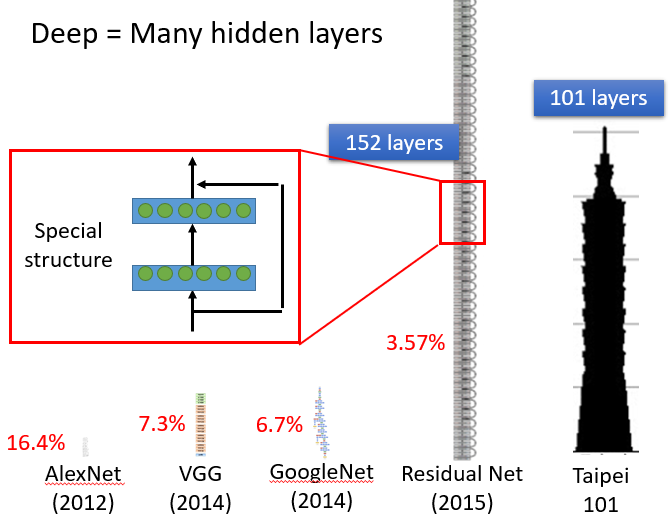
• 2012 AlexNet：8层
• 2014 VGG：19层
• 2014 GoogleNet：22层
• 2015 Residual Net：152层
• 101 Taipei：101层

随着层数变多，错误率降低，随之运算量增大，通常都是超过亿万级的计算。对于这样复杂的结构，我们一定不会一个一个的计算，对于亿万级的计算，使用loop循环效率很低。

本质：通过隐藏层进行特征转换

把隐藏层通过特征提取来替代原来的特征工程，这样在最后一个隐藏层输出的就是一组新的特征（相当于黑箱操作）而对于输出层，其实是把前面的隐藏层的输出当做输入（经过特征提取得到的一组最好的特征）然后通过一个多分类器（可以是softmax函数）得到最后的输出y。

矩阵计算

计算方法就是：sigmoid（权重w【黄色】 * 输入【蓝色】+ 偏移量b【绿色】）= 输出

我们引入矩阵计算来加速计算过程，神经网络在推算特征的过程本质上是空间向量的一系列变化

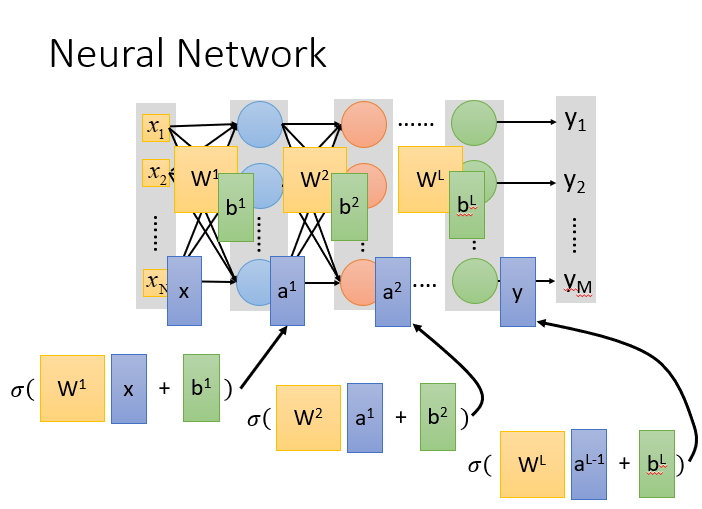
为了防止卷积网络出现无效层，所以我们引进激活函数。

因为在通过一系列的变化层的过程中，如果每次变化是线性的，那么多个相邻的神经层就有可以合并隐藏的可能，这会使得整个卷积网络设计显得低效而且愚蠢，更重要的是，非线性变化有助于改变向量本身的结构，使得函数输出约束在一定的范围内，防止出现爆内存等情况。

神经网络的一些设计问题：

• 多少层？ 每层有多少神经元？
  这个问我们需要用尝试加上直觉的方法来进行调试。对于有些机器学习相关的问题，我们一般用特征工程来提取特征，但是对于深度学习，我们只需要设计神经网络模型来进行就可以了。对于语音识别和影像识别，深度学习是个好的方法，因为特征工程提取特征并不容易。
• 结构可以自动确定吗？
  有很多设计方法可以让机器自动找到神经网络的结构的，比如进化人工神经网络（Evolutionary Artificial Neural Networks）但是这些方法并不是很普及 。
• 我们可以设计网络结构吗？
  可以的，比如 CNN卷积神经网络（Convolutional Neural Network ）

Step2: 模型评估

对于一个训练模型，我们往往使用Loss函数来评估其训练的好坏，对于一个神经网络而言我们采用**交叉熵（cross entropy）**来评判一个网络是否准确。

什么是交叉熵？

该长度（把来自一个分布q的消息使用另一个分布p的最佳代码传达的平均消息长度）称为交叉熵。 形式上，我们可以将交叉熵定义为：

注意，交叉熵 不是对称的 。

那么，为什么要关心交叉熵呢？ 这是因为，交叉熵为我们提供了一种表达两种概率分布的差异的方法。 和 的分布越不相同， 相对于 的交叉熵将越大于 的熵。

用交叉熵作为损失函数

交叉熵常用来作为分类器的损失函数。不过，其它类型的模型也可能用它做损失函数，比如生成式模型。

我们有数据集 ，其中， 是特征值或输入变量； 是观察值，也是我们期待的模型的输出，最简单的情况是它只有两个离散值的取值，比如 ，或者 ，或者 。能根据新的 对 做出预测的模型就是我们常用的二元分类器（Binary Classifier）。

我刻意没有选用 作为例子，是为了避免有人认为我们观察到的数据 就是概率向量，因而可以直接套用 和模型的输出 之间的交叉熵作为损失函数。实际上，我们可以使用交叉熵作为分类器的损失函数的根本原因是我们使用了最大似然法，即我们通过在数据集上施用最大似然法则从而得到了与交叉熵一致的目标函数（或者损失函数）。我们观察原始数据时是看不到概率的，即使 ，它的取值0或1只是客观上的观察值而已，其概率意义是我们后来人为地加给它的。

总体损失

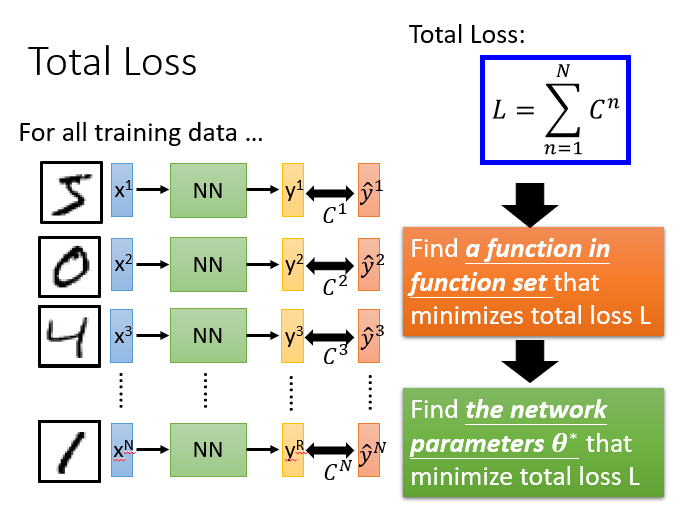
对于损失，我们不单单要计算一笔数据的，而是要计算整体所有训练数据的损失，然后把所有的训练数据的损失都加起来，得到一个总体损失L。接下来就是在function set里面找到一组函数能最小化这个总体损失L，或者是找一组神经网络的参数θ，来最小化总体损失L

Step3：选择最优函数

具体流程：θ是一组包含权重和偏差的参数集合，随机找一个初试值，接下来计算一下每个参数对应偏微分，得到的一个偏微分的集合∇L就是梯度,有了这些偏微分，我们就可以不断更新梯度得到新的参数，这样不断反复进行，就能得到一组最好的参数使得损失函数的值最小

为什么我们需要深度学习？

一个神经网络如果权重和偏差都知道的话就可以看成一个函数，他的输入是一个向量，对应的输出也是一个向量。不论是做回归模型（linear model）还是逻辑回归（logistics regression）都是定义了一个函数集（function set）。我们可以给上面的结构的参数设置为不同的数，就是不同的函数（function）。这些可能的函数（function）结合起来就是一个函数集（function set）。这个时候你的函数集（function set）是比较大的，是以前的回归模型（linear model）等没有办法包含的函数（function），所以说深度学习（Deep Learning）能表达出以前所不能表达的情况。

(转载自知乎阿力阿哩哩)

目前业界有句话被广为流传：

“ 数据和特征决定了机器学习的上限，而模型与算法则是逼近这个上限而已。 ”

因此，特征工程做得好，我们得到的预期结果也就好。

那特征工程到底是什么呢？在此之前，我们得了解特征的类型：文本特征、图像特征、数值特征和类别特征等。我们知道计算机并不能直接处理非数值型数据，那么在我们要将数据灌入机器学习算法之前，就必须将数据处理成算法能理解的格式，有时甚至需要对数据进行一些组合处理如分桶、缺失值处理和异常值处理等。

这也就是特征工程做的事：提取和归纳特征，让算法最大程度地利用数据，从而得到更好的结果。

不过，相较于传统的机器学习，深度学习的特征工程会简单许多，我们一般将数据处理成算法能够理解的格式即可，后期对神经网络的训练，就是提取和归纳特征的过程。

这也是深度学习能被广泛使用的原因之一：特征工程能够自动化。

反向传播

关于反向传播，其背后的思想与动态规划问题有类似之处，以最简单的01背包为例

我们已知在容量为5，可取为1的最优解，那么可以递推容量为5，可取为2的最优解，层层递进而且过程可以反向转化。

反向传播的过程本质上也是一种特征传递的过程。

李宏毅机器学习第五章任务

如何解决机器学习内出现的训练问题

局部最小值与鞍点（saddle point）

在梯度下降法中，通常当梯度为零时终止运算，并默认此点为全局最优点(local minima)。但这种方法有缺陷，即可能到达鞍点(saddle points)而难以前进。鞍点处函数梯度等于0，但函数值并非局部最小，如图所示：

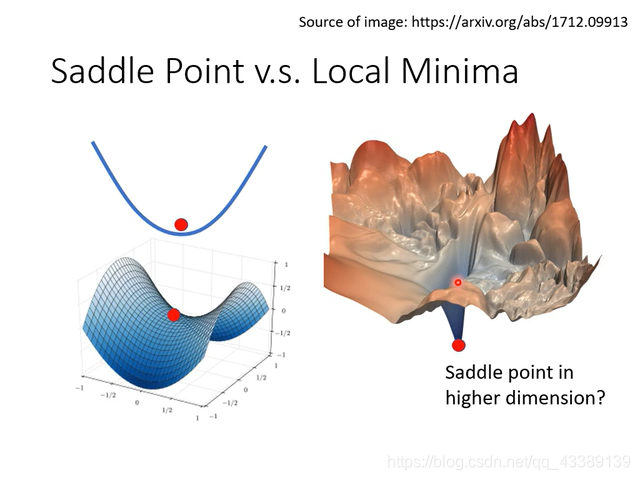
那么如何避免最终梯度下降在鞍点处呢？

这里我们可以引入二次导数来解决这个问题

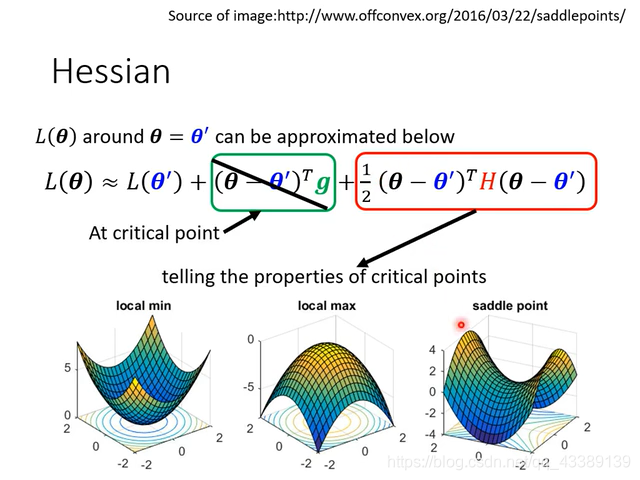
通过观察鞍点以泰勒展开的结过后发现如果在鞍点处，其二次导数往往向我们指出了下一步的前进方向，也就是说，二次导数可以指导我们梯度下降的方向。

但在实际问题中，我们往往要处理的是多维度，多变量的回归问题，在多维空间内很难再产生马鞍点现象。

批次（batch）与动量（Momentum）

什么是batch 和 Momentum？

batch

batch字面上是批量的意思，在深度学习中指的是计算一次cost需要的输入数据个数。

Momentum：(动量，冲量)

结合当前梯度与上一次更新信息，用于当前更新,可以防止在更新落入驻点时数据不再更新前进。

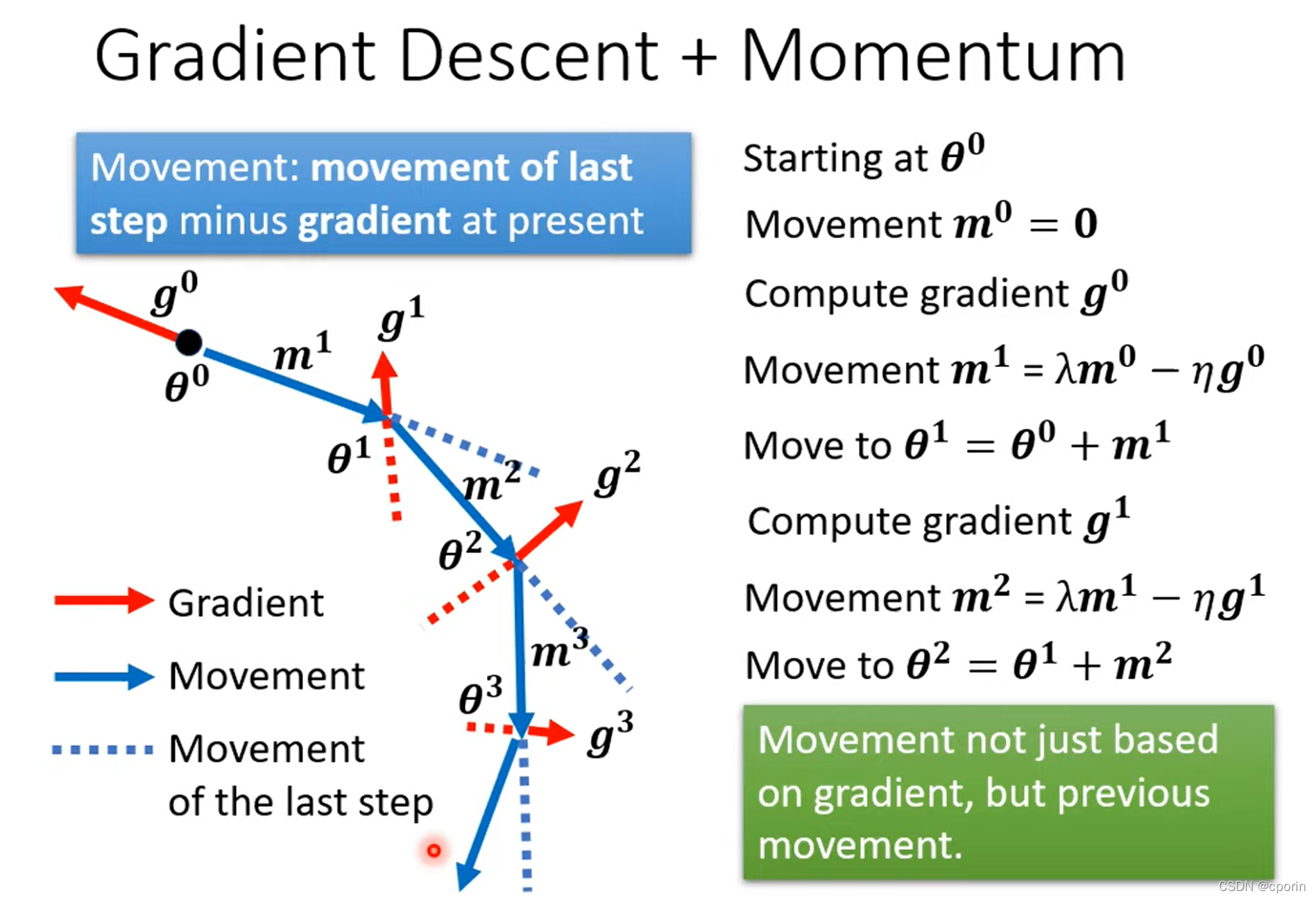
详解batch

如何利用batch进行优化？

在实际的最优化过程中，我们将很多的数据分成好多份，每一份算出一个L i
出来，然后使用它迭代计算θ ∗

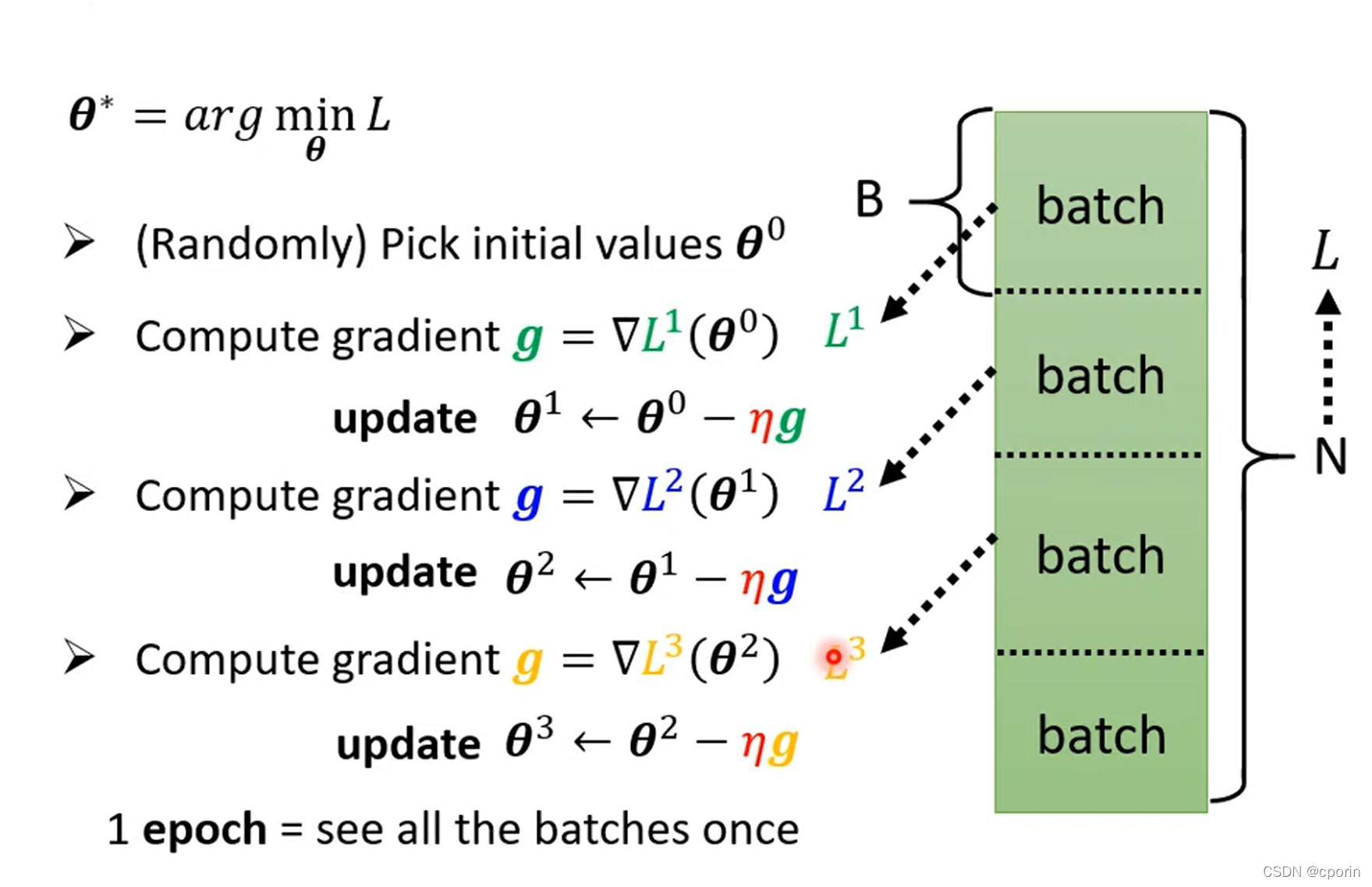
update：是使用一个batch中的数据训练出的L 迭代一次。
epoch：使用每一个batch迭代过一次θ ，每一个epoch之后会重新分配batch进行训练（Shuffle）。

Small batch

将一批数据分割成多个batch，这样每一个epoch会更新多次，更新次数增多，但每次更新的方向不一致，容易受到干扰。

但是对于Small batch 而言，可以避免在梯度下降的过程中落在鲁棒性较差的sharp minima内。

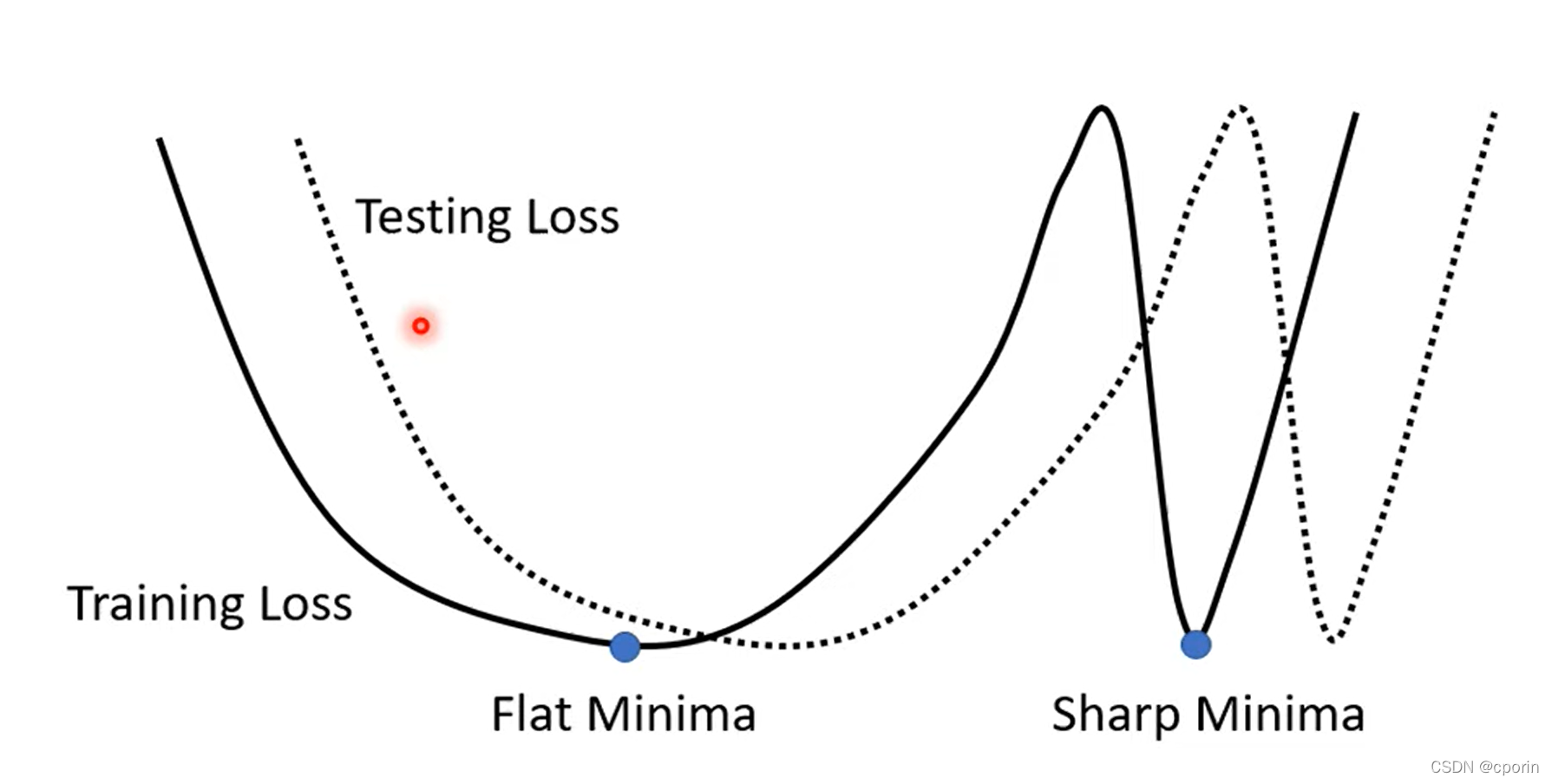
因为在一些需要中我们需要鲁棒性更高的模型来处理问题，对于训练数据更好的拟合模型往往存在一定的适配问题，较小的batch就能很好的解决这个问题。

Large batch

将一批数据仅仅进行简单分割，每组batch内含有大量数据，一个epoch迭代的次数少，每次更新时间长，方向更加稳定。

但是在GPU越来越作为计算主力的今天，很多运算往往能够并发进行，Large batch甚至在一定范围内的性能优于Small batch。

Small batch VS Large batch

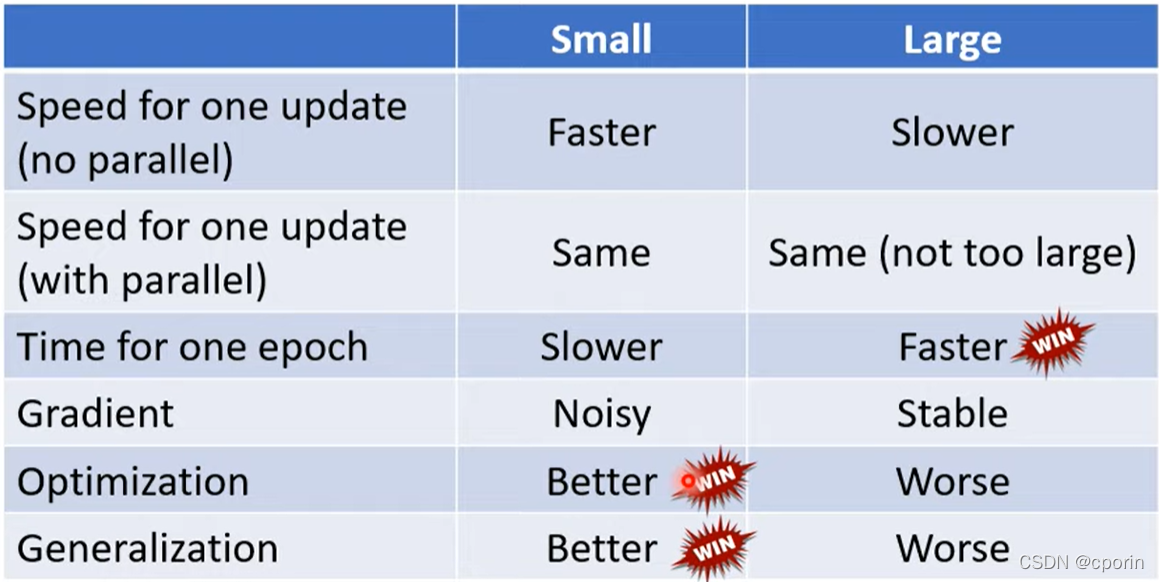
调整自适应的学习率

前面我们在讨论如何进行梯度下降时就有讨论这一问题，当学习率一定时，容易卡在梯度较小而并非minima 的位置，这时就需要我们对学习率进行调整。

Root mean square

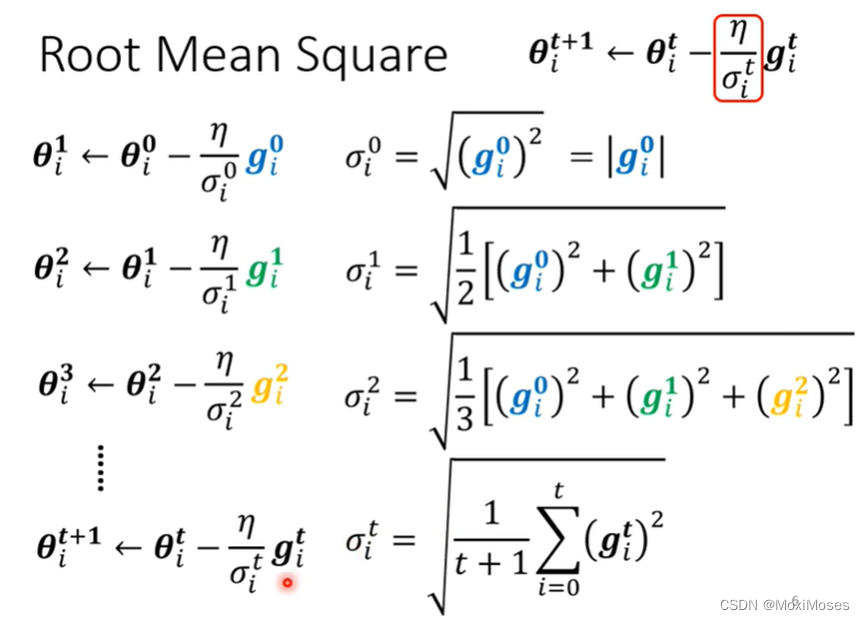
当坡度比较大时，gradient就比较大，σ就比较大，所以learning rate就比较小。当坡度比较小时，gradient就比较小，σ就比较小，所以learning rate就比较大。因此，有了σ后，我们就可以随着参数的不同，自动地调整learning rate的大小，而当参数过大或者过小时，之前的参数变化能够对这一变化产生修正。

可能存在的问题

因为之前我们把所有的gradient拿来做平均，所以在纵轴的方向，初始的位置gradient很大，过了一段时间过后，gradient就会很小，于是纵轴就累积到了很小的σ，步伐就会变大，于是就爆发时喷射。当走到gradient很大的时候，σ就会变大，于是步伐就会变小，因此就会出现图中的情况。
之前的η一直是固定值，但应该把它跟时间联系在一起。这里要用到最常用的策略是Learning Rate Decay，这样我们就可以很平稳地走到终点。当越靠近终点时，η就会越小，当它想乱喷的时候，乘上一个很小的η，就可以平稳到达终点。

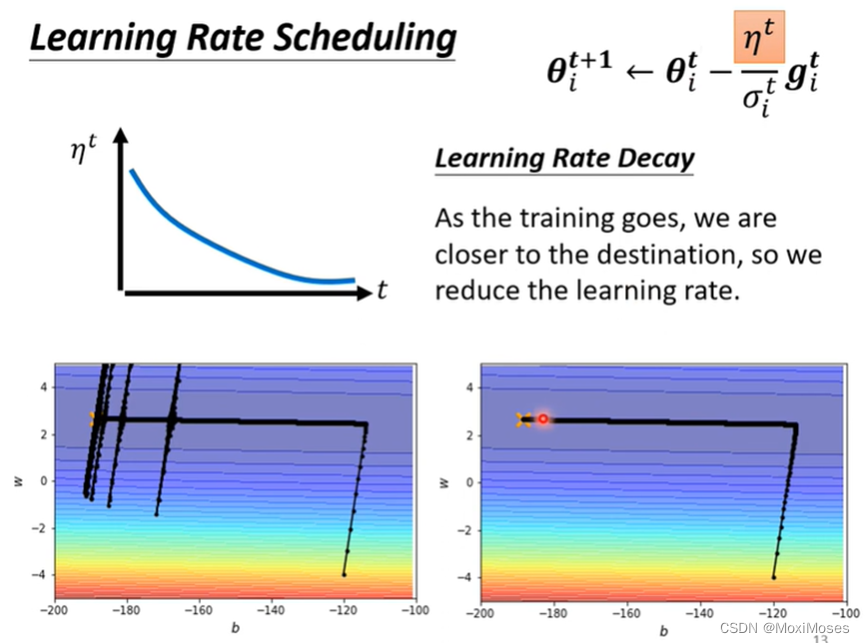
RMSProp

RMSProp第一步和Root Mean Square是一样的，在下面的步骤中不一样的是在计算Root Mean Square时，每一个gradient都有同等的重要性，在RMSProp中，你可以调整它的重要性。

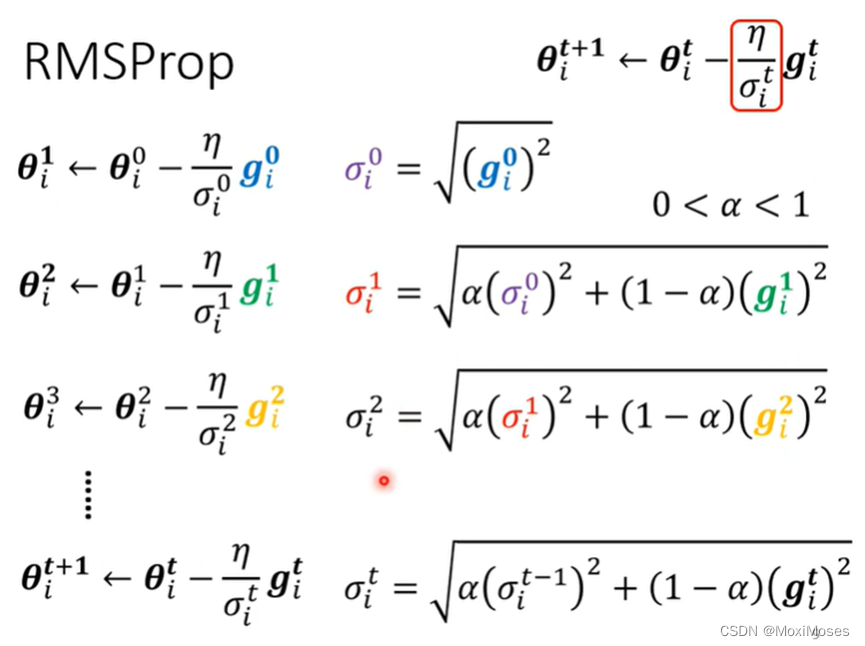
α如果设很小趋近于0时，就对与我们计算出来的gradient比较重要；α如果设很大趋近于1时，就对与我们计算出来的gradient比较不重要。我们现在动态调整σ。图中的黑线是error surface。在陡峭的地方gradient会变大，我们就把α设小，就可以很快地把σ的值变大，也就可以把步伐变小；在平坦的地方gradient会变小，我们就把α设大，就可以很快地把σ的值变小，也就可以把步伐变大。

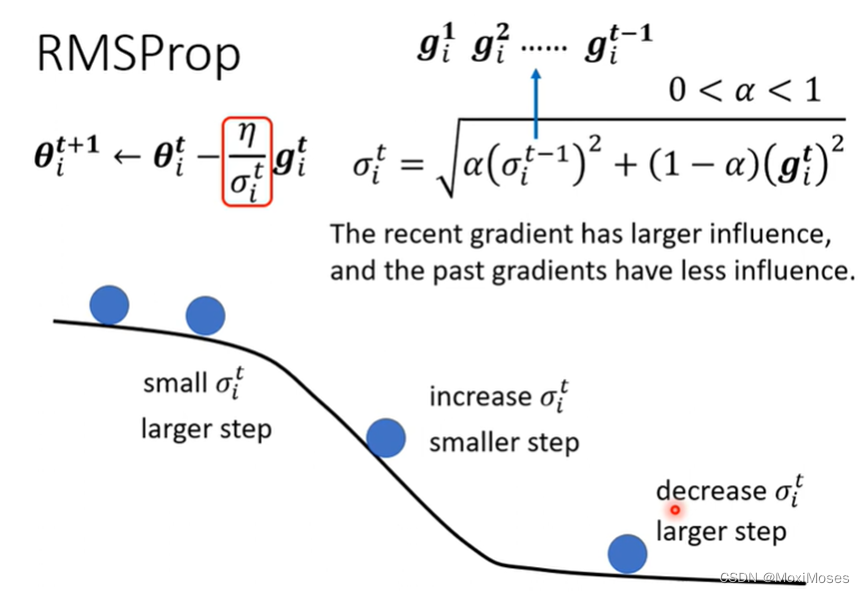
Adam: RMSProp + Momentum

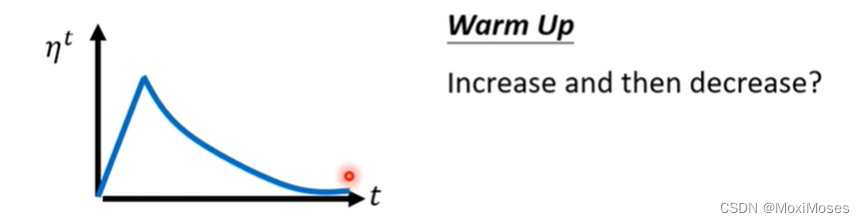
Warm Up

Warm Up它是让Learning Rate先变大后变小，具体变大到多少，这个需要自己手动调整。为什么要用Warm Up？因为在使用Adam RMS Prop和Adagrad的时候，我们要计算σ，σ告诉我们某一个方向是陡峭还是平滑，但这需要多笔数据才能让统计更加精准。一开始我们的收集不够精准，所以要先收集有关σ的统计数据，等到足够精准后，再让Learning Rate上升。

Summary of Optimization

1． 这里我们添加了Momentum，现在不是顺着gradient的方向来更新参数，而是把之前全部的gradient的方向，做一个总和来当做更新的方向。
2． 如下图所示，这里需要除以gradient的Root Mean Square。Momentum直接把所有的gradient加起来，它会考虑方向；而Root Mean Square只考虑大小，不考虑方向。

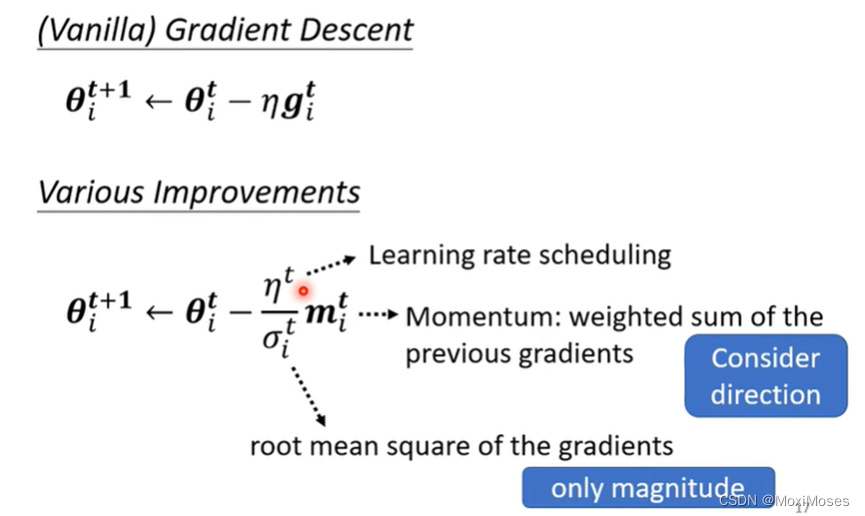
损失函数(Loss)也可能有影响

如果要求处理多分类问题，例如分为 1，2，3 三类问题，不对输出结果做处理很容易引发误差，例如相邻之间的元素更容易判断。

这时我们就需要对类别做处理，使用one-hot vector来解决整个情况。就是将类别划分为向量

1：【1，0，0】

2：【0，1，0】

3：【0，0，1】

然后对所计算的结果经过softmax后，得到y ′ ，然后才去计算y ′到y ^的距离。

Softmax

Softmax从字面上来说，可以分成soft和max两个部分。max故名思议就是最大值的意思。Softmax的核心在于soft，而soft有软的含义，与之相对的是hard硬。很多场景中需要我们找出数组所有元素中值最大的元素，实质上都是求的hardmax。

下面给出Softmax函数的定义（以第i个节点输出为例）：

，其中 为第i个节点的输出值，C为输出节点的个数，即分类的类别个数。通过Softmax函数就可以将多分类的输出值转换为范围在[0, 1]和为1的概率分布。

Softmax将输出层转化为对应分类的概率，并且由于指数函数的特性，它能够很快地将大数据与小数据之间产生差别。

交叉熵（Cross-Entropy）

这个暂时不太懂…等待日后补充。

批次标准化（Batch Normalization）

在训练损失下降的过程中，Loss的大小本身依然受制于数据

假如数据过大，参数减小时，可能使Loss变化过大，就会对回归（regression）产生影响。

我们要做的就是尽量减小这种行为带来的影响。

批标准化好处

我们知道数据预处理做标准化可以加速收敛，同理，在神经网络使用标准化也可以加速收敛，而且还有更多好处。

具有正则化的效果（抑制过拟合）
提高模型的泛化能力
允许更高的学习速率从而加速收敛。

批标准化有助于梯度传播，因此允许更深的网络。对于有些特别深的网络，只有包含多个BatchNormalization层时才能进行训练。

批标准化的实现过程

1.求每一个训练批次数据的均值
2.求每一个训练批次数据的方差
3.数据进行标准化
4.训练参数 γ，β
5.输出γ通过γ与β的线性变换得到原来的数值
在训练的正向传播中，不会改变当前输出，只记录下γ与β。
在反向传播的时候，根据求得的γ与β通过链式求导方式，求出学习速率以至改变权值。

李宏毅机器学习第六章任务

卷积网络（CNN）

什么是卷积网络

卷积神经网络属于前馈网络的一种，是一种专门处理类似网格数据的神经网络，其特点就是每一层神经元只响应前一层的局部范围内的神经元。

卷积网络一般由： 卷积运算+非线性操作（RELU）+池化 +若干全连接层 。

卷积网络之所以叫做卷积网络，是因为这种前馈网络其中采用了卷积的数学操作。在卷积网络之前，一般的网络采用的是矩阵乘法的方式，前一层的每一个单元都对下一层每一个单元有影响。

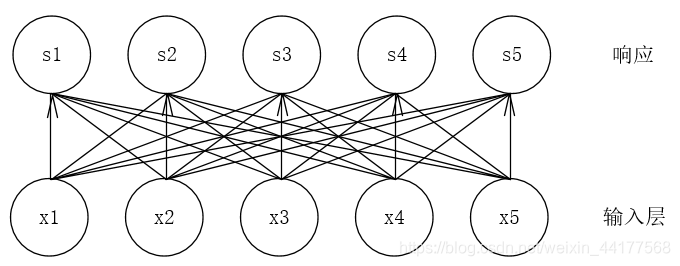
卷积网络：

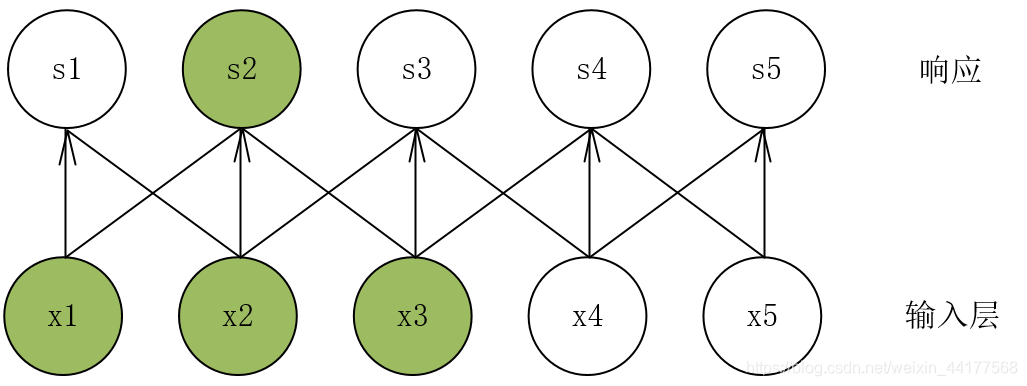
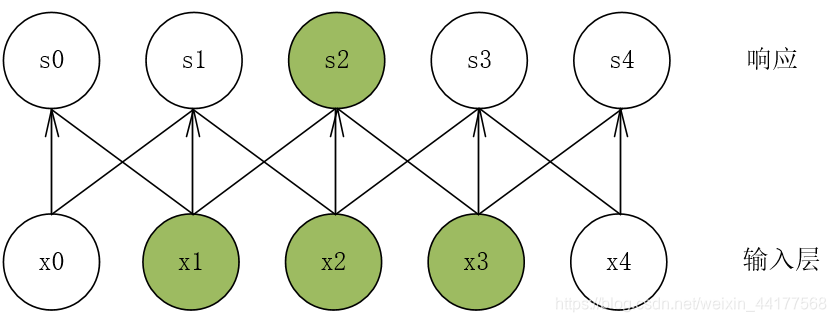
响应层中的每一个神经元只受到输入层的局部元素的影响。以s2为例，它仅仅受到x1、x2、x3的影响，是一种稀疏的连接方式。

为什么使用卷积网络（卷积网络的优势）

传统神经网络都是采用矩阵乘法来建立 输入和输出之间的关系 ，假如我们有 M 个输入和 N个输出，那么在训练过程中，我们需要 M×N 个参数去刻画输入和输出的关系 。当 M 和 N都很大，并且再加几层的卷积网络，这个参数量将会大的离谱。

卷积网络是如何处理这个问题的呢？

稀疏连接

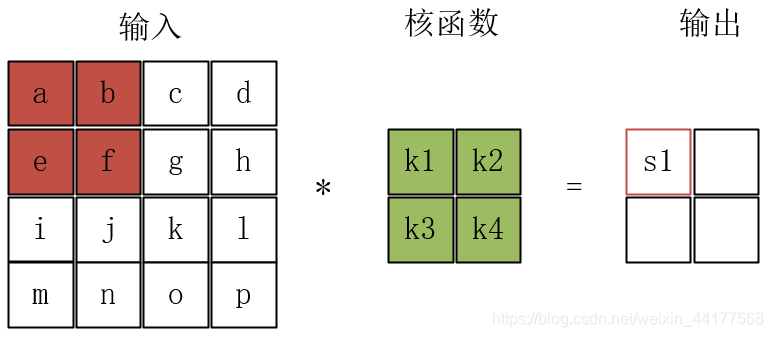
卷积操作通过核函数将信息提取在了一个部分。

通过filter的不断移动，最终输入的矩阵被简化。

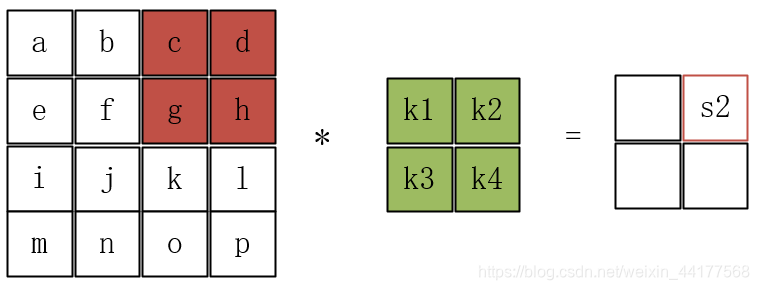
通过CNN网络简化，流入下一级的变量将不再需要把所有的原始数据传输进去，后面的响应层只需要处理部分信息。

参数共享

由于filter的不变性，在卷积化的过程中我们只需要指定一个卷积核，通过卷积的数据所需要的参数大大减少，而且由于步长和核函数的性质，我们可以视作传入的数据在进入下一层神经网络时一部分将会共用同一函数，降低了模型复杂度。

平移不变性

平移不变性：如果一个函数的输入做了一些改变，那么输出也跟着做出同样的改变，这就时平移不变性。

平移不变性是由参数共享的物理意义所得。在计算机视觉中，假如要识别一个图片中是否有一只猫，那么无论这只猫在图片的什么位置，我们都应该识别出来，即就是神经网络的输出对于平移不变性来说是等变的。

一下图为例：s2只和x1、x2、x3有关

输入层数据向左移动一位：其中响应层的s2也只和x1、x2、x3有关，只是位置发生了稍微的变化

池化（pooling）

最大池化（Max pooling）

这个过程可以视为filter变成了一个Max函数，筛选出区域内的最大值

平均池化（Average pooling）

这个过程可以视为filter变成了一个求均值的函数，求出区域内矩阵元素的平均值

池化的意义

最大池化和平均池化有利于筛选出需要的主要元素，增强训练模型的鲁棒性，进行特征选择，另一方面可以解决过拟合问题。

文中转载链接：https://blog.csdn.net/weixin_44177568/article/details/102812050

Flatten

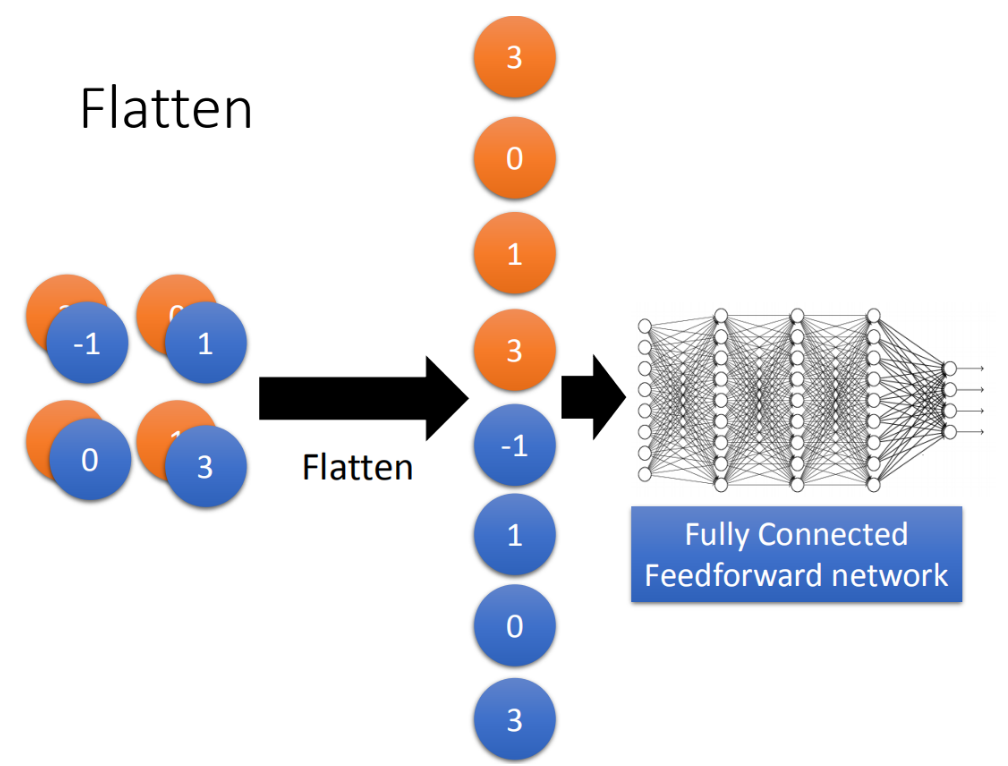
flatten就是feature map拉直，拉直之后就可以丢到fully connected feedforward netwwork，然后就结束了。

CNN的应用

对于一个图像而言，我们可以使用多个卷积核来处理图像，从而得到不同灰度，不同特征的图像，在辨识物品图像中有重要作用。

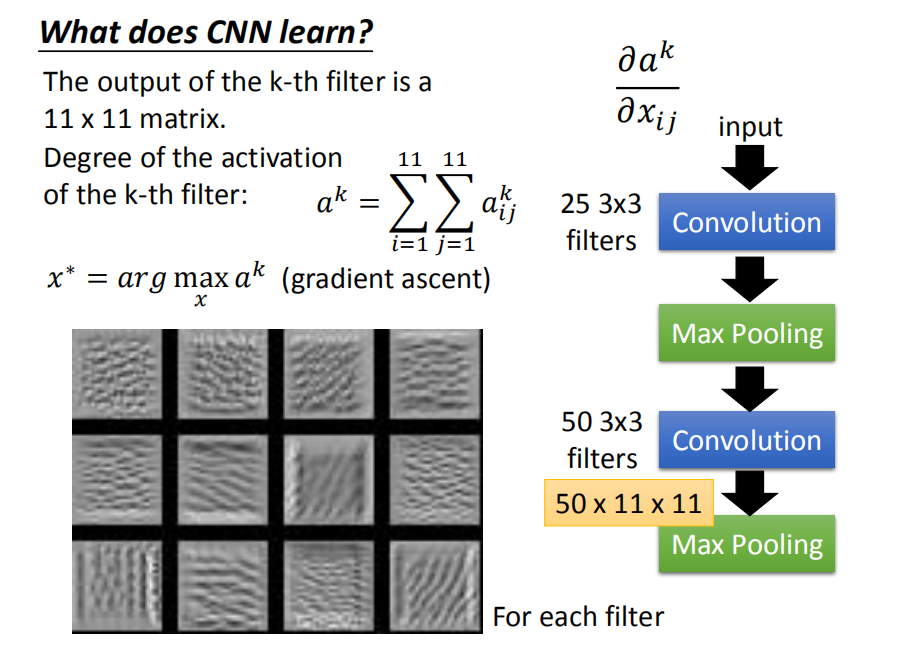
同时CNN在处理出现相同模式，或者一个模式多次出现的应用场景有较强优势。

为什么要进行深度学习？

模组化

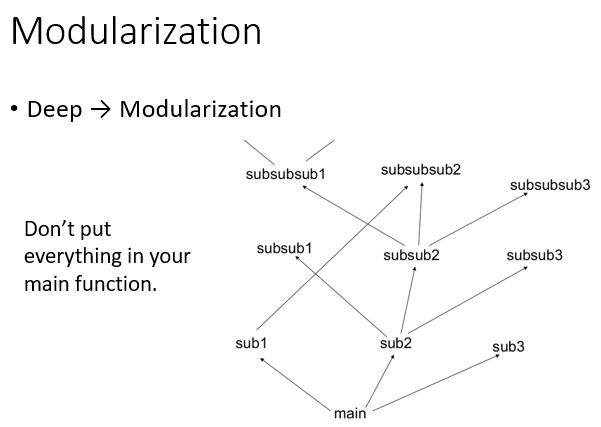
当我们在做deep learning的时候，很多function被不断的重复使用，从结构上看，深度学习的结构更清晰，而且避免了设计的重复。

端到端的学习

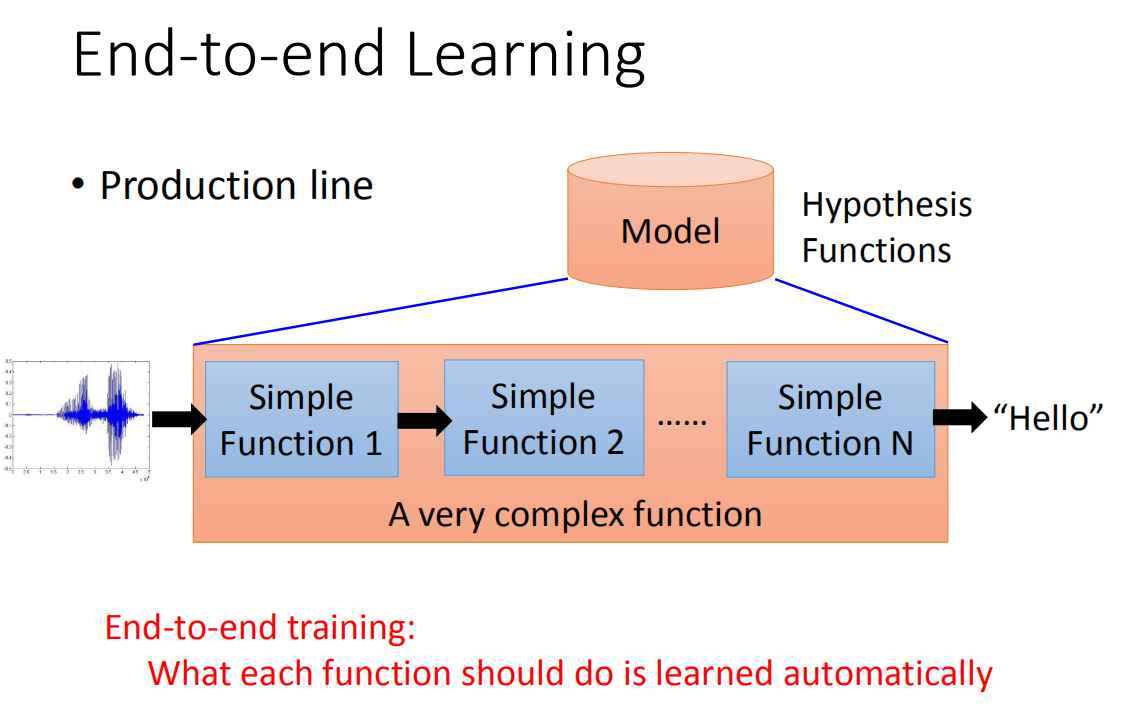
当我们用deep learning的时候，另外的一个好处是我们可以做End-to-end learning。

所谓的End-to-end learning的意思是这样，有时候我们要处理的问题是非常的复杂，比如说语音辨识就是一个非常复杂的问题。那么说我们要解一个machine problem我们要做的事情就是，先把一个Hypothesis funuctions(也就是找一个model)，当你要处理1的问题是很复杂的时候，你这个model里面它会是需要是一个生产线(由许多简单的function串接在一起)。比如说，你要做语音辨识，你要把语音送进来再到通过一层一层的转化，最后变成文字。当你多End-to-end learning的时候，意思就是说你只给你的model input跟output，你不告诉它说中间每一个function要咋样分工(只给input跟output，让它自己去学)，让它自己去学中间每一个function(生产线的每一个点)应该要做什么事情。

那在deep learning里面要做这件事的时候，你就是叠一个很深的neural network，每一层就是生产线的每一个点(每一层就会学到说自己要做什么样的事情)

其余的内容在前面已经提及，在这里不再赘述。

半监督学习（Semi-supervised Learnings）

半监督学习的生成模型

前面部分与监督学习的操作一样，先使用有监督的数据估计出 P(Ci)、μi 和 Σ，接下来使用未标记的数据 xu 来对这些参数重新估计，以二分类问题为例，估计过程主要分为如下两个步骤：

初始化 θ={P(C1),P(C2),μ1,μ2,Σ}，（可以随机初始化，也可以根据已有的标记数据估计出来）。

step1 ：根据初始化的参数计算无标记数据的后验概率Pθ(C1|xu) 。

step2 ：更新模型参数：

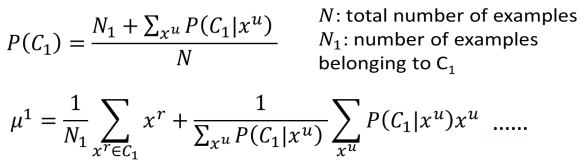
解释如下：

利用已训练好的模型对unlabelled data 进行评估，得到更新后的P（C1），与μ1等参数，再带入更新θ的式子内

• 接着再返回 step1，直到参数收敛为止。
• 其实上面这个过程，我们用到了再机器学习领域一个超级NB的算法的思想，它就是EM(Expectation-maximization),step1就是 E，step2就是 M. 这样反复下去，在最终一定会收敛

半监督学习之低密度分离假设（Low-density Separation）

• 在用这个假设的时候，需要假设有一个很明显的区域(Low-density),能够把数据分开。Self-training
• 先对有标记数据训练出一个模型f*,这个可以模型可以用任何方法训练。
• 用这个 f∗ 来预测无标记的数据，预测出的就叫 pseudo label.
• 接下来，就用无标记数据中拿出一部分数据，放到有标记数据中，怎么选出这部分是自己定的，也可以对每一个数据提供一个权重。新加入了这些数据之后，就可以再重新训练一个 f∗，往复进行。
• 这招用在 regression 中，是没有用的，因为用预测出来的数字重新用来做训练，并不会影响模型的参数。
• 在做 self-training 时，其实就是把某个未标记数据指定一个分类，而在 generative model 中，其实就是把未标记数据对应于各个分类的概率计算出来。

基于熵的正则化(Entropy-based Regularization)

假如未标记数据数据 xu 经过某一组参数估计后属于某一类的概率如下:

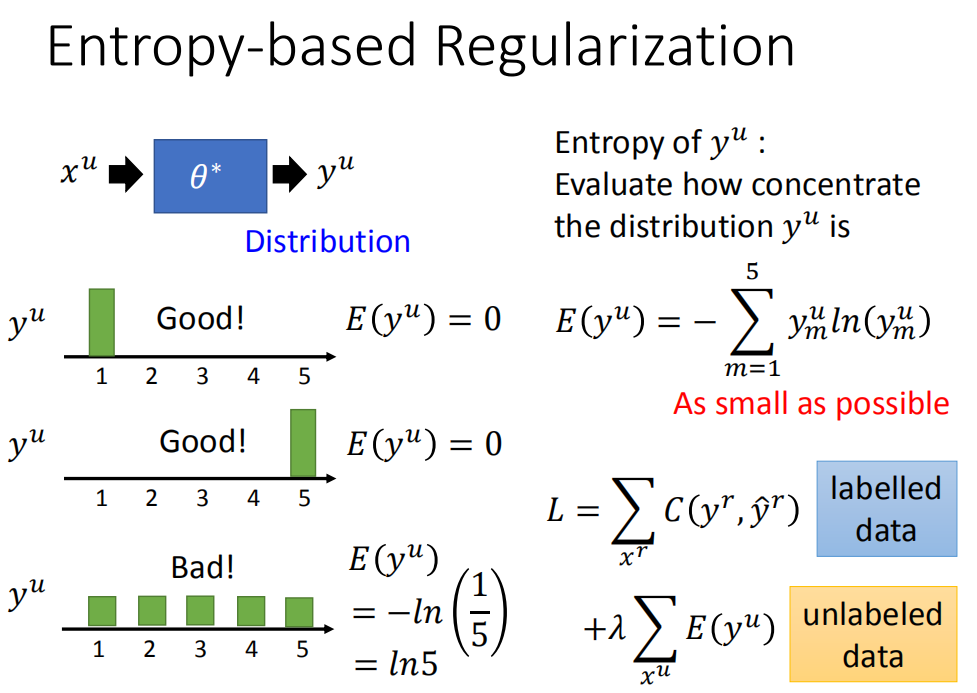
又边红圈中的公式为熵的计算公式。由上图可知 xu 属于某一类的概率越大，熵的值E就越小，因此重新定义损失函数

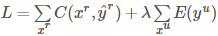
，其中E(yu)可以微分，我们可以直接用梯度下降法来求解。

Semi-supervised SVM

参考博客链接 Semi-Supervised Support Vector Machines(S3VMs)_extremebingo的博客-CSDN博客

平滑假设(smoothness assumption)

位于稠密数据区域的两个距离很近的样例的类标签相似，也就是说，当两个样例被稠密数据区域中的边连接时，它们在很大的概率下有相同的类标签；相反地，当两个样例被稀疏数据区域分开时，它们的类标签趋于不同。

基于图的方法

我们用Graph-based approach来表达这个通过高密度路径连接这件事情。就说我们现在把所有的data points都建成一个graph，每一笔data points都是这个graph上一个点，要想把他们之间的range建出来。有了这个graph以后，你就可以说：high density path的意思就是说，如果今天有两个点，他们在这个graph上面是相的(走的到)，那么他们这就是同一个class，如果没有相连，就算实际的距离也不是很远，那也不是同一个class。

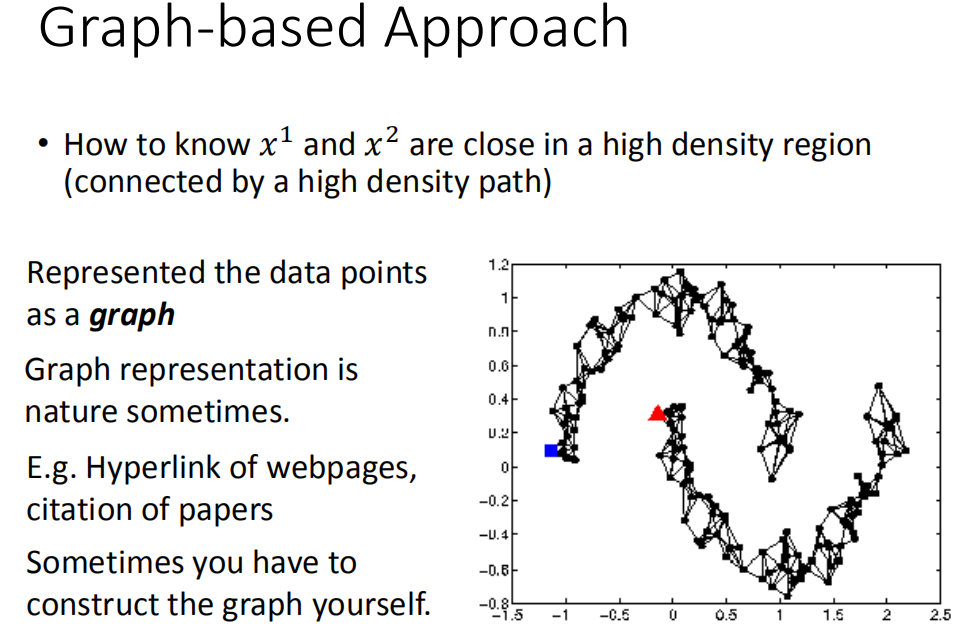
关于如何确立树和建立节点，实际上这个过程就是对原有数据的再挖掘与分析，将其特征分成一个又一个可处理的节点，处理的结果就是节点的通过率，也可以视为相似度。