- 1若依系统在linux上部署,前台dist文件使用nginx服务,接口无法正常使用的问题?_若依前端打包 无法访问您的文件怎么办
- 2springboot影院购票与管理系统 计算机专业毕设源码02845_基于springboot线上电影售票系统文献综述
- 3怎样速成python?_python3天速成
- 4这篇深入浅出贴助你早日实现Stable Diffusion自由 | 京东云技术团队
- 5Programming Abstractions in C阅读笔记:p303-p305
- 6如何使用rpm卸载命令_rpm 卸载
- 7从另一页面调用html代码_Dubbo测试环境服务调用隔离这么玩对么
- 8Java中的public关键字详解_java public
- 92022美赛A题自行车到底怎么骑_22年美赛自行车
- 10Android 11 重打包对齐错误_failure [-124: failed parse during installpackagel
【小白学机器学习5】偏差bias, 方差,var 误差error, MSE, RMSE,MAE, MAPE, WMAPE
赞
踩
目录
2.2.2 方差和真实值完全没有关系,至少从定义和公式上看是这样
3.2 如何评价某函数的预测值是否足够好? 如何比较不同的预测函数的预测值的好坏呢?
3.5 MSE 均方差损失( Mean Squared Error Loss)
1 各种误差的相关定义
- 方差 Variance
- 偏差 bias
- 误差 error
- 残差
- Deviance
- MSE
- MAE
2 偏差和方差
2.1 偏差 bias
2.1.1 偏差的定义
- 偏差:描述的是预测值(估计值)的期望与真实值之间的差距。
- 偏差越大,越偏离真实数据。
2.1.2 偏差的公式和求法
- Bias=E(f(xi))-Y
- 其中i=1~n,E(f(xi))是n个 f(xi)的期望
- 每一个真实值,可能有N个估计值/预测值,而这N个估计值只有1个期望值,
- 所以偏差是比较每1个真实值和其n个估计值的期望之间的误差。
2.2 方差 Variance
2.2.1 方差的定义
- 方差:描述的是预测值的变化范围,离散程度,也就是离其(预测值整体)期望值的距离。
- 方差越大,数据的分布越分散
- 预测值和真实值完全没关系。
2.2.2 方差和真实值完全没有关系,至少从定义和公式上看是这样
- 方差小只是一群估计值自身的属性,够不够聚拢,发散是否厉害。
- 有可能方差很大也可能很小,但偏离真实值很远的情况。
2.3 方差的公式和求法
- U 总体均值
- Ux 样本均值
- N 总体数量
- n 样本数量
2.3.1 总体方差
- δ**2=Σ(xi-U)**2/N,其中i=1~n
- 如果还是我们要看的目标是预测值f(xi) ,那么把f(xi) 替换xi就得到
- 如下对预测值f(xi)的方差
- δ**2=Σ(f(Xi)-average(f(Xi)))**2/n
- #从公式里看和真实值没有丝毫关系,只和 预测值 f(xi) 这一群数据有关系
2.3.2 样本方差(实际方差 /统计方差)
- 实际中,总体平均数很难获得
- 统计中的方差(样本方差)是每个样本值与全体样本值的平均数之差的平方值的平均数
- 如果还是我们要看的目标是预测值f(xi) ,那么把f(xi) 替换xi就得到
- 如下对预测值f(xi)的方差
- S**2=Σ(xi-Ux)**2/(n-1)
- S**2=Σ(f(Xi)- average(f(Xi)))**2/(n-1)
- #从公式里看和真实值没有丝毫关系,只和 预测值 f(xi) 这一群数据有关系
2.4 标准差 standard deviation
- 标准差= sqrt(方差)
2.5 偏差和方差的区别
网上流传了很多的图,解释的很清楚了

2.6 偏差和方差的统一性:误差=方差+偏差**2+ε
2.6.1 误差的公式可以统一两者的意义
偏差和方差可以统一在一起
- 误差=偏差**2+方差+ irreducible error
- 即误差Err / 偏差Bias / 方差Var / 不可避免的标准差σ
- Error=Irreducible Error+{\color{Blue} Bias^{2}}+{\color{DarkGreen} Variance}
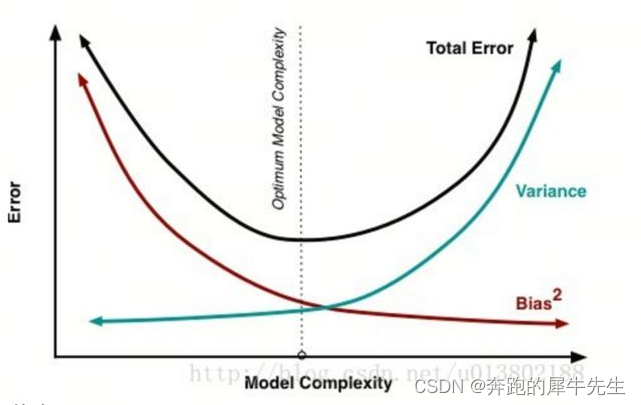
2.6.2 误差来源有三个
- 第1个: irreducible Error:基于总体分布
- 因为是总体分布的离散度,所以Irreducible不可避免;总体用模型Y=f(X)+ε描述。
- Irreducible Error,即不可避免误差部分,刻画了当前任务任何算法所能达到的期望泛化误差的下限
- 即刻画了问题本身的难度;
- 第2个:Bias:基于样本分布和真实值之间的比较
- 总体点和样本点 : 样本的期望值 和总体值/真实值之间的差距
- Bias,即偏差部分,刻画了算法的拟合能力
- Bias偏高表示预测函数与真实结果相差很大;
- 第3个: Var:基于样本分布
- 预测点集/样本点集的离散度:预测值本身的离散程度,和真实值无关。
- Variance,即方差部分,则代表 “同样大小的不同数据集训练出的模型” 与 “这些模型的期望输出值” 之间的差异。
- 训练集变化导致性能变化,Var高表示模型很不稳定。
2.7 偏差和方差的一般性应用的区别
测各种预测模型的比较来说
- 一般来说,如果模型越复杂,参数越多,偏差越小,但方差可能会越大,可能存在过拟合情况
- 一般来说,如果模型越简单,参数越小,偏差越大,但方差可能会越小,可能存在拟合不够的情况。
- 而理论上理想中的模型是,偏差低,方差也低的模型。
3 从误差说起
3.1 误差的由来
- step1: 假设我们有自变量X,因变量Y,
- step2: 我们经过计算和模拟得到模拟函数/预测函数 f(X)
- step3: 然后我们用预测函数 f(X) 去模拟Y
- step4: 但是预测函数和真实值之间一定是有误差的,Y=f(X)+ ε
3.2 如何评价某函数的预测值是否足够好? 如何比较不同的预测函数的预测值的好坏呢?
- 真实值:Y ,真实值可能有多个
- 预测值:Y^=f(x) ,对应每一个真实值,对应的预测值根据预测函数可做出多个
- 然后现在怎么判断,预测值是否准确呢?
- 就到了最小二乘法了。
3.3 最小二乘法:应该叫最小乘方法
3.3.1 最小二乘法
最小二乘法:应该叫最小乘方法,二乘就是指平方!这个名字不直观,很容易误导我这样的新手。
最小二乘法误差=Σ(Y-f(xi))**2


3.3.2 插播知识: 什么是范式和L1,L2范式
- 简单的理解,范式就是距离
- L1 范式距离,就是 |y1-y2|
- L2 范式距离,就是 (y1-y2)**2
- 以下类推
- 像我现在的水平,暂时了解到这么多即可。
3.4 评价误差的各种标准
从最小二乘这个评价标准开端,又衍生了各种各有优劣的评价方法和指标
- 最小二乘法误差=Σ(Y-f(xi))**2
- MSE
- RMSE
- MAE
- MAPE
- WMAPE
3.5 MSE 均方差损失( Mean Squared Error Loss)
- MSE 均方差损失( Mean Squared Error Loss)
- L2范式误差
- L2 loss
3.5.1 计算公式
- MSE,均方误差
- MSE=Σ(Y-f(Xi))**2/i ,i=1~n
- MSE=最小二乘误差/n

3.5.2 图形推导
推导
- MSE=Σ(y^-y)^2/n
- 这个函数的抽象化
- MSE=y=f(x)
- MSE=y=f(x)=f(x^2)
- 这个图形是个二次曲线,有最小值
- 范围[0,+∞),当预测值与真实值完全相同时为0,误差越大,该值越大
- MSE 曲线的特点是光滑连续、可导,便于使用梯度下降算法,是比较常用的一种损失函数。
- 而且,MSE 随着误差的减小,梯度也在减小,这有利于函数的收敛

3.5.3 MSE的特点
- 不同商品真实值量纲上的差别带来的MSE结果波动大
- 极端值的影响,可以平衡
- [0,1] 误差越小,平方值的MSE会越小
- [1,∞] 误差越大,平方值的MSE会越大,惩罚性的把误差越大
- 不够直观(平方之后含义不好解释)
- 其中,y^为预测值,y为真实值。
- 对每期预测值和实际值的差值进行平方,然后再对多期差值的平方取平均值,得到平均均方误差。
- 平方的好处是放大极端误差:对误差进行平方,就是加倍“惩罚”那些极端误差,凸显那些极端虚高或虚低的预测值,也是我们应该重点避免的对象。
- 选择预测方法时,要尽量避免产生大错特错、极端误差的预测模型,用均方误差来量化预测准确度,能较好地排除这样的模型。
- 平方误差有个特性,就是当 yi 与 f(xi) 的差值大于 1 时,会增大其误差;
- 当 yi 与 f(xi) 的差值小于 1 时,会减小其误差。这是由平方的特性决定的。
- 也就是说, MSE 会对误差较大(>1)的情况给予更大的惩罚,对误差较小(<1)的情况给予更小的惩罚。
- 从训练的角度来看,模型会更加偏向于惩罚较大的点,赋予其更大的权重。
- 如果样本中存在离群点,MSE 会给离群点赋予更高的权重,但是却是以牺牲其他正常数据点的预测效果为代价,这最终会降低模型的整体性能。

3.6 RMSE
RMSE,开方均方误差 RMSE=sqrt(MSE)
Root Mean Square Error

![]()
3.7 MAE
3.7.1 L1 loss
- MAE
- L1 loss
3.7.2 计算公式
MAE=Σ|Y-f(Xi)|/n ,i=1~n

3.7.3 图形推导

3.7.4 MAE的特点
- 不同商品真实值量纲上的差别带来的MAE结果波动大
举例子
- 比如同样是 |yi^-yi|=5
- 有可能是6-1=5,但是百分比percent=(6-1)/1=5=500%,误差很大
- 也可能是105-100=5,但是百分比percent=(105-100)/100=5/100=5%,误差较小
- 也可能是1005-1000=5,但是百分比percent=(1005-1000)//1000=5/1000=0.5%,误差极小
- 可见,ABS都是5,但是百分比差别巨大!!
- MAE 的曲线呈 V 字型,连续但在 y-f(x)=0 处不可导,计算机求解导数比较困难。
- 而且 MAE 大部分情况下梯度都是相等的,这意味着即使对于小的损失值,其梯度也是大的。
- 这不利于函数的收敛和模型的学习。
- 值得一提的是,MAE 相比 MSE 有个优点就是 MAE 对离群点不那么敏感,更有包容性。
- 因为 MAE 计算的是误差 y-f(x) 的绝对值,无论是 y-f(x)>1 还是 y-f(x)<1,没有平方项的作用,惩罚力度都是一样的,所占权重一样。

3.8 MAPE
Mean Absolute Percentage Error

- 当真实值
非常小,特别是接近0时,MAPE可能很大
- 这个值很直观,但也容易误导:当实际值非常小,特别是接近0时,这一百分比可能很大;
- 如果实际值是0的话,分母就是0,计算没有意义。解决方案是设定上限,比如平均绝对百分比误差不超过100%。
- MAPE 指平均绝对百分比误差,是一种相对度量,实际上将 MAD 尺度确定为百分比单位而不是变量的单位。平均绝对百分比误差是相对误差度量值,它使用绝对值来避免正误差和负误差相互抵消
- MAPE 对相对误差敏感,不会因目标变量的全局缩放而改变,适合目标变量量纲差距较大的问题

3.9 WMAPE


- 极端值带来的误差波动小
3.10 R^2


参考文档
http://www.360doc.com/content/17/1217/10/40769523_713767996.shtml
https://zhuanlan.zhihu.com/p/26061758?from_voters_page=true
https://www.jianshu.com/p/301766de458d
机器学习中的方差和偏差理解_low-variance-CSDN博客
使用Excel进行线性回归、计算R2、RMSE、MAE等精度方法_rmse怎么用excel-CSDN博客
MAE, MSE, RMSE, R方 — 哪个指标更好? - 知乎
回归预测模型的常见评估指标(MAE,MSE,MAPE等) - 知乎
深度学习常用损失MSE、RMSE、MAE和MAPE-CSDN博客
https://www.cnblogs.com/hider/p/17095700.html
机器学习——需求预测——准确性(误差)统计——MAE、MSE、MAPE、WMAPE-CSDN博客
https://blog.csdn.net/htuhxf/article/details/84585022


