- 1yjk只算弹性的不计算弹塑性_【YJK】弹性时程分析如何考虑周期折减系数
- 2RecyclerView 拖动/滑动多选的实现(2)_android拖动多选功能
- 3MagicAnimate:一张照片,让TikTok小姐姐跳舞
- 4wpf chartcontrol 绑定数据_WPF界面开发:你真知道如何将数据绑定到Chart3D中吗?
- 5vue中this.$router.push()路由传值和获取的两种常见方法
- 6uni-cloud 基础介绍 【前端写接口不愁】_unicloud的构成
- 7.Net Core 6 web api jwt 一直 401 Postman返回WWW-Authenticate Bearer没有其他提示的解决方法_c# net6 jwtbearer 401
- 8源码分析vue响应式原理_vue dep.js
- 9[含泪解决]OSError: [Errno 99] Cannot assign requested address__踩坑记录——app.py绑定IP失败
- 10iOS崩溃日志分析_崩溃代码applebcmwlan
一看就会!四种策略改进的蜣螂算法求解三维无人机路径规划!原理公式详解!附赠与原算法对比!出图美观直接用!_蜣螂算法改进
赞
踩
目录
大家在改进智能优化算法的时候,传统的工程应用已经吸引不了审稿人的注意,非常容易被拒稿!今天为大家带来一期多策略改进的蜣螂算法求解三维无人机路径规划代码,适合作为创新点!同时也附赠与原DBO算法的对比,具体代码已放在最后,需要代码的朋友可直接拉到最后~
学会这一篇后,其他优化算法也可以替换!可随机导入地图!也可导入固定地图!
先上结果图:
无人机路径规划结果三维图

无人机路径规划结果二维图

迭代200次后,算法的收敛曲线图:
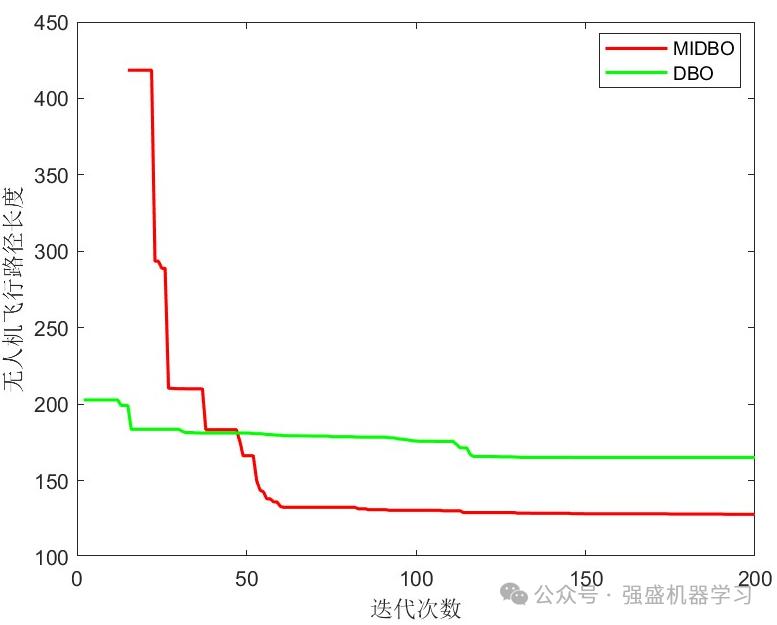
注意!细心的小伙伴可能会发现某些算法或多次运行后并不是从0开始迭代显示迭代次数,这是因为无人机三维路径规划与其他的应用不一样,需要考虑多种约束条件,较为复杂,因此可能前几次迭代还没有找到飞行路径长度,到后期才开始找到并显示,这是非常正常的情况!
当然,这里我因为时间关系只运行了200次,实际操作500次或1000次可能会运行出更好的效果!可根据自己的需求进行调整!
迭代200次后,两种算法的飞行路线直方图:
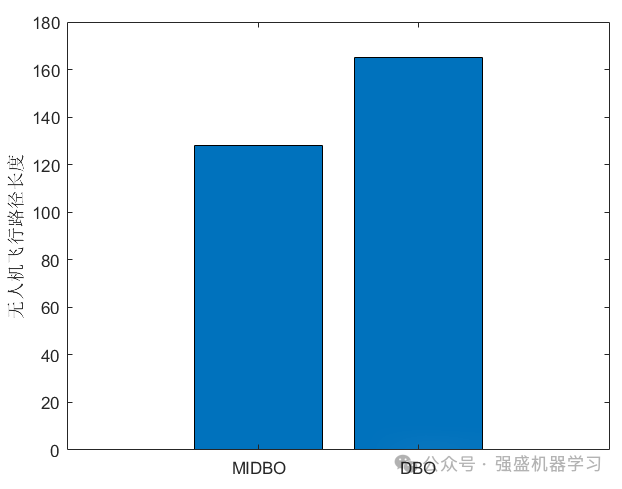
可以看到,改进后的MIDBO比原始DBO路径长度有明显减少,但也请注意,由于优化算法具有较强随机性,未必每一次运行的效果均相同~
改进蜣螂算法原理详解:
首先看看我们的蜣螂算法是如何改进的:
改进点1:改进雏球和偷窃蜣螂对最优解的接受程度
雏球和偷窃蜣螂会不停的向局部最优位置和全局最优位置靠近,但在算法前期,应尽量扩大群体的搜索范围,快速向局部最优位置或全局最优位置靠近虽然能使算法快速收敛,但也有一定的概率令算法陷入停滞,导致无法收敛到全局最优解。因此,设计一种根据蜣螂搜索能力的强弱(适应度大小)动态改变雏球和偷窃蜣螂对局部最优位置或全局最优位置的接受程度的策略。具体方法如下:将蜣螂群体根据搜索能力(适应度值优劣)排序,雏球和偷窃蜣螂根据自身搜索能力的更新位置方式如下:
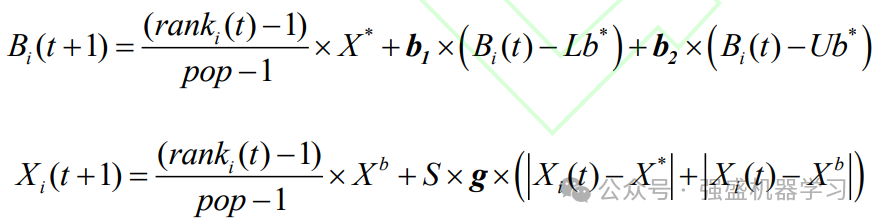
改进点2:麻雀搜索算法追随者位置更新机制
麻雀搜索算法(SSA)是受麻雀觅食行为和反捕食行为启发而提出的新型群智能算法,麻雀根据个体适应度的不同分为发现者、追随者和侦查者。发现者适应度值高,占群体数量的 10%-20%,为追随者提供觅食区域与方向。在麻雀种群中,追随者负责跟随发现者寻找食物,追随者的位置更新如下式:
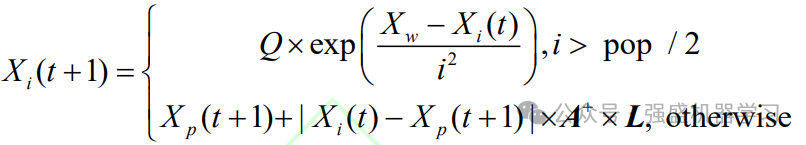
改进点3:麻雀搜索算法追随者位置更新机制
SSA具有收敛精度高、收敛速度快、鲁棒性强等特点,在函数优化问题方面,优于粒子群算法,灰狼优化算法等群智能算法。因此,将麻雀搜索算法中追随者的位置更新机制作为一种扰动策略引入蜣螂优化算法,定义麻雀搜索算法中的发现者最优位置对应蜣螂优化算法中的全局最优位置。若扰动性太强,群体容易陷入混乱无序状态;若扰动性太弱,扰动策略将不能发挥作用;因此,根据迭代深度自适应改变扰动概率,并采用贪婪策略决定是否保留此次扰动,扰动概率如下式所示:
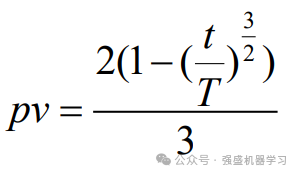
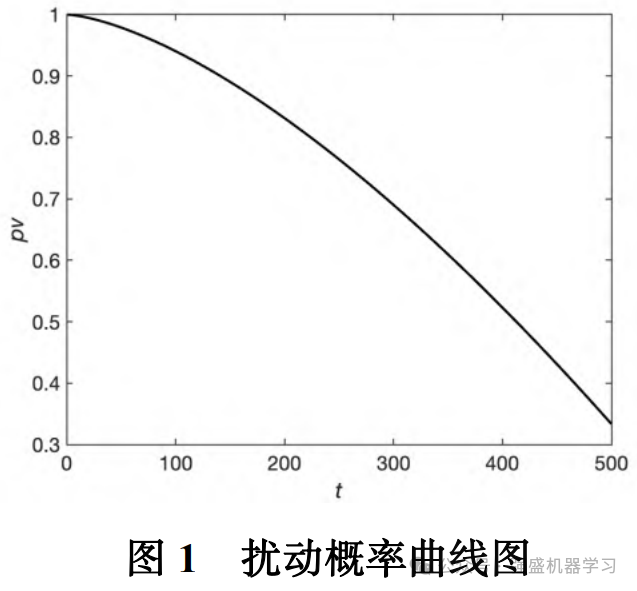
由图可知,在迭代前期,扰动概率较大,可充分发挥麻雀追随机制扰动的作用,达到提升种群质量,提高算法寻优性能的作用;在迭代后期,扰动概率逐渐减小,起到加快算法收敛速度的效果。具体扰动步骤如下:a)根据式(13)计算第i个个体的扰动概率pv;b)生成随机数rÎ(0,1),若r<pv,进行步骤c,否则第i个个体不进行扰动;c)生成随机数r1Î(0,1),若r1< ST,根据式(12)中的第二个公式生成新解,否则根据式(12)中的第一个公式生成新解,经过大量实验证明ST=0.7时效果最好,因此本文取ST=0.7,这意味着群体中有70%的个体往群体最优位置方向变异,30%个体朝比自身更差的位置变异;d)计算新解的适应度值,若优于扰动前适应度值,用新解代替扰动前的解,否则,该次扰动无效。
改进点4:柯西高斯变异
引入麻雀搜索算法追随机制的扰动主要作用是使群体能更充分的遍历解空间,提升种群质量,类似于混沌扰动;在多峰值情况下,蜣螂优化算法和其他群智能优化一样,容易陷入局部最优解,柯西高斯变异是为应对多峰值情况而提出的辅助策略,加大算法跳出局部最优解的概率,提升算法的寻优精度。在每次麻雀搜索算法追随机制扰动后,判断群体是否早熟,判断方式为:若群体经过 5 次迭代后最优解不变,则判定算法陷入停滞(早熟), 对整个群体采用柯西高斯变异策略,令群体跳出局部最优解,柯西高斯变异方法如下式:
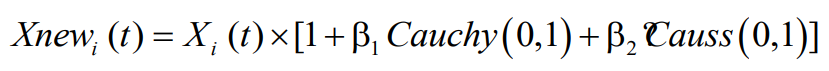
该算法复现的是2023年12月15日刚发表于北大核心、CSCD核心期刊《计算机科学与探索》上的一篇文章,具体策略和思路可查看如下参考文献,你先用,你就是创新!
[1]郭琴,郑巧仙.多策略改进的蜣螂优化算法及其应用[J/OL].计算机科学与探索:1-22[2024-02-02].

原文作者采用的是20个基准测试函数和 CEC2019 测试函数进行验证,并将 MIDBO 运用在汽车碰撞优化问题的求解上。实际上这个汽车碰撞也是一个工程约束优化问题,不算新颖!这里不过多赘述,接下来主要讲下我们的三维无人机路径规划模型!
三维无人机路径规划模型原理详解:
一、环境模型
将地理位置信息航迹规划的环境模型飞行区域设置为 100×100×100 的直角坐标区域,障碍物区域建模采用山峰模型,其数学表达式为:
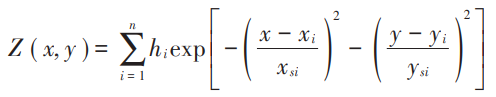
式中:(xi,yi)是第i个山峰的中心坐标;hi为地形的高度参数;xsi和ysi分别是第i个山峰沿着x轴和y轴的衰减量、控制坡度;n表示山峰总个数。
二、飞行路径及平滑处理
飞行路径原来是由第i个粒子位置点连接的直线段组成,路径上包含起点ps(xs,ys,zs)、终点pg(xg,yg,zg)和飞行路径上的其他粒子位置点pij(xij,yij,zij),其中,j=1,2,⋯,n,n为粒子位置点的个数,这些位置点及起点、终点共同组成飞行路径,路径由{ps,pi1,pi2,⋯,pin-1,pin,pg}组成。连接这些点后得到的飞行路径为一条折线,位置点为折线顶点。为了缩短飞行路径的大小,找出平滑的飞行路径,采用三次B样条插值的方法,将间断的散点进行插值,并绘制出平滑的飞行路径曲线。
(1)路径平滑基函数及粒子位置点




(2) 曲线插值
式(9)由4个控制点控制 ,设控制点坐标为 (Xi,Yi,Zi)(i=1,2,⋯,n),曲线插值后任意点的坐标(Xt,Yt,Zt )表示为:
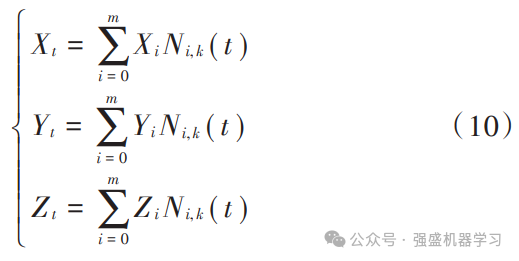
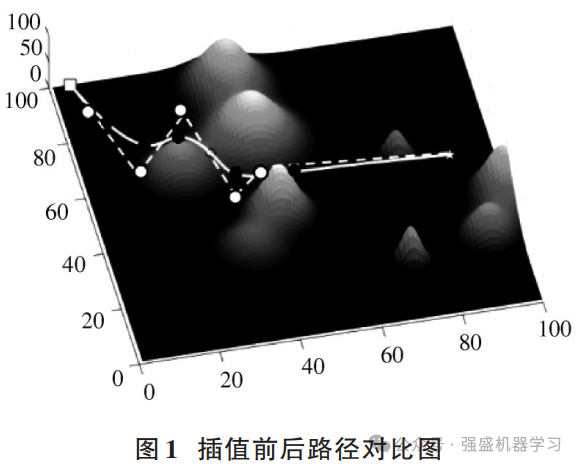
根据式(9)和式(10)就可以得出平滑的飞行路径曲线,平滑效果图如图1所示。
三、约束条件
约束条件的目的是保证无人机飞行路径在指定空域内,并且可以有效规避障碍物,所以提出了两个主要的约束条件。
1)为保证飞行路径在指定空域内进行,需要满足以下约束:

2)为避免无人机与地形内的障碍物相撞,需满足:
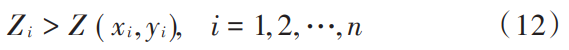
四、目标函数
无人机的飞行路径的目标函数主要由三部分组成,分别是无人机总飞行航程、绕过障碍物的代价和在规定边界内飞行的代价。无人机总目标函数表达式如下:
![]()
式中:Vc代表无人机的总航程代价;Tc代表无人机绕飞障碍物的代价;Ec代表无人机在规定边界内飞行的代价。
航程代价Vc主要考虑无人机从起点到终点的总飞行距离,是各个弧段Li之和,如果总航迹由n段组成,那么航程总代价表达式为:
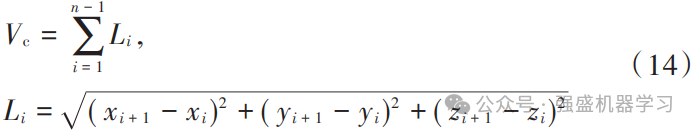
地形代价Tc主要是为了确保无人机飞行路径避开障碍物,通过控制Tc值的大小来实现。当高度zi高于所在地形中障碍物高度z2(xi,yi)时,取Tc=0;当高度zi低于所在地形中障碍物高度z2(xi,yi)时,取Tc=∞。这样求和后能够保证无人机飞行路线可以规避山峰等障碍物。表达式如下:

边界代价Ec是为了确保无人机在指定空域内,主要通过控制Ec值的大小来实现。当在空域内时,Ec=0;当不在空域内时,Ec=∞。这样求和后能够保证粒子是在指定空域内取得。表达式如下:

以上就是该无人机三维路径规划的核心原理!具体文献可参考:
[1]胡观凯,钟建华,李永正等.基于IPSO-GA算法的无人机三维路径规划[J].现代电子技术,2023,46(07):115-120.
在具体写作过程中,如果觉得字数太多,可以重点写目标函数和约束条件即可!
部分代码展示(Matlab语言):
- close all
- clear
- clc
- warning off;
-
- %% 三维路径规划模型定义
- global startPos goalPos N
- N=2; % 待优化点的个数(可以修改)
- startPos = [10, 10, 80]; % 起点(可以修改)
- goalPos = [80, 90, 150]; % 终点(可以修改)
- SearchAgents_no=30; % 种群大小(可以修改)
- Function_name='F2'; % F1:随机产生地图 F2:导入固定地图
- Max_iteration=200; % 最大迭代次数(可以修改)
- % Load details of the selected benchmark function
- [lb,ub,dim,fobj]=Get_Functions_details(Function_name);
- AlgorithmName={'MIDBO','DBO'}; % 算法名称
- addpath('./AlgorithmCode/') % 添加算法路径
- bestFit=[]; % 保存各算法的最优适应度值
- for i=1:size(AlgorithmName,2) % 遍历每个算法,依次求解当前问题
- Algorithm=str2func(AlgorithmName{i}); % 获取当前算法名称,并将字符转换为函数
- [Best_score,Best_pos,Convergence_curve]=Algorithm(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);%当前算法求解
- %将当前算法求解结果放入data中
- data(i).Best_score=Best_score; % 保存该算法的Best_score到data
- data(i).Best_pos=Best_pos; % 保存该算法的Best_pos到data
- data(i).Convergence_curve=Convergence_curve; % 保存该算法的Convergence_curve到data
- bestFit=[bestFit data(i).Best_score];
- end
- save data data

完整代码获取:
点击下方小卡片,后台回复关键字,不区分大小写:
无人机01
如果想将该无人机模型换成其他新颖优化算法,如:2024年的冠豪猪CPO、牛顿-拉夫逊优化算法NRBO、美洲狮优化算法PO、2023年的霜冰优化算法、减法平均优化器,或者鲸鱼算法、灰狼算法等等所有优化算法,均可点击下方小卡片后后台私信,看到后会秒回~



