devbox
从前慢现在也慢
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

【十分钟速成系列】--遗传算法（GA）（含py代码）_快速遗传算法

作者：从前慢现在也慢 | 2024-03-07 22:35:18

赞

踩

快速遗传算法

目录

1.算法前瞻：

1.1 基因和染色体:

 1.2 种群和个体

1.3 适应度函数

1.4交叉

轮盘赌法：

单点交叉

多点交叉 

1.5变异

2.算法步骤

2.1编码和解码

二进制编码：

二进制解码：

2.2 初始化种群

2.3 适应度和选择

2.4 交叉和变异

2.5 算法终止 

2.6 算法流程图

3.应用场景 

4.遗传算法的基本特征

5.代码实现 

1.算法前瞻：

                遗传算法简称GA（Genetic Algorithms）模拟自然界生物遗传学（孟德尔）和生物进化论（达尔文）通过人工方式所构造的一类 并行随机搜索最优化方法，是对生物进化过程--优胜劣汰，适者生存--这一过程进行的一种数学仿真。

我们首先介绍一下遗传算法中的几个概念：

1.1 基因和染色体:

        细胞是所有生物的基石。由此可知，在一个生物的任何一个细胞中，都有着相同的一套染色体。所谓染色体，就是指由 DNA 组成的聚合体。

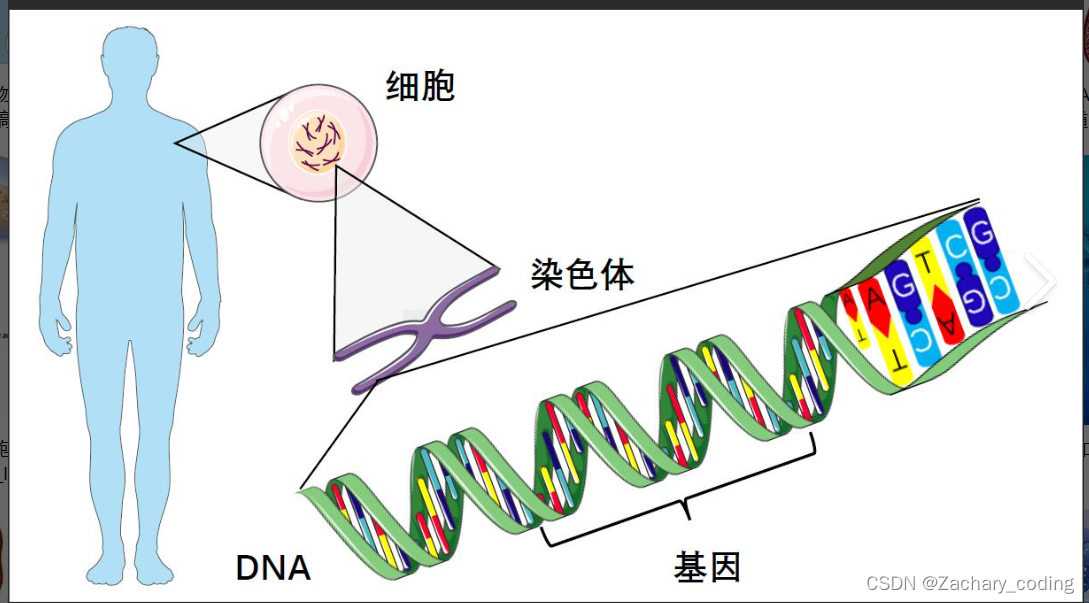
         一条染色体由基因组成，这些基因其实就是组成 DNA 的基本结构，DNA 上的每个基因都编码了一个独特的性状。

 1.2 种群和个体

                遗传算法启发自进化理论，而我们知道进化是由种群为单位。

                种群是什么：在生物学上，是在一定空间范围内同时生活着的同种生物的全部个体。个体通常为某个问题的一个解，并且该解在计算机中被编码为一个向量。

1.3 适应度函数

                适应度(Fitness)：各个个体对环境的适应程度叫做适应度。为了体现染色体的适应能力，引入了对问题中的每一个染色体都能进行度量的函数，叫适应度函数。这个函数通常会被用来计算个体在群体中的优良等级。

1.4交叉

遗传算法每一次迭代都会生成N条染色体，在遗传算法中，这每一次迭代就被称为一次“进化”。那么，每次进化新生成的染色体是如何而来的呢？——答案就是“交叉”，你可以把它理解为交配。

交叉的过程需要从上一代的染色体中寻找两条染色体，一条是爸爸，一条是妈妈。然后将这两条染色体的某一个位置切断，并拼接在一起，从而生成一条新的染色体。这条新染色体上即包含了一定数量的爸爸的基因，也包含了一定数量的妈妈的基因。

轮盘赌法：

现在我们知道父母，那如何选择父亲和母亲呢，我们采用轮盘赌法.

想象有一个轮盘，现在我们将它分割成 m 个部分，这里的 m 代表我们总体中染色体的个数。每条染色体在轮盘上占有的区域面积将根据适应度分数成比例表达出来。

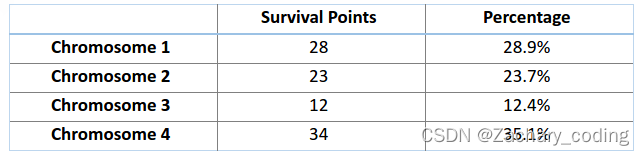
建立如下「轮盘」

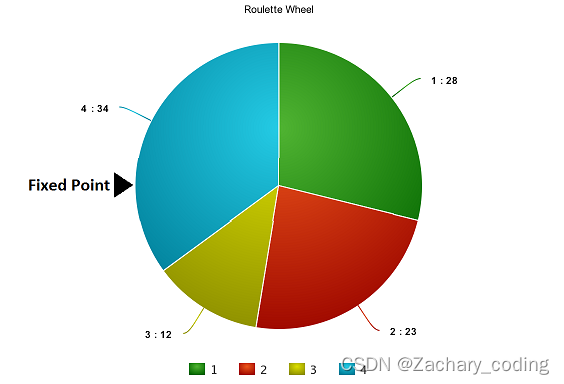
轮盘开始旋转，我们将被图中固定的指针（fixed point）指到的那片区域选为第一个亲本。然后，对于第二个亲本，我们进行同样的操作 。这样就完成了父母的选择。

单点交叉

随机选择一个交叉点，然后，将交叉点前后的染色体部分进行染色体间的交叉对调，于是就产生了新的后代。

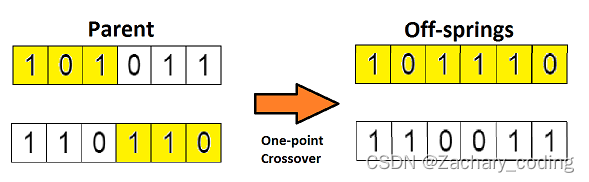
多点交叉 

设置两个交叉点，那么这种方法被成为「多点交叉」

1.5变异

交叉能保证每次进化留下优良的基因，但它仅仅是对原有的结果集进行选择，基因还是那么几个，只不过交换了他们的组合顺序。这只能保证经过N次进化后，计算结果更接近于局部最优解，而永远没办法达到全局最优解，为了解决这一个问题，我们需要引入变异。

变异很好理解。当我们通过交叉生成了一条新的染色体后，需要在新染色体上随机选择若干个基因，然后随机修改基因的值，从而给现有的染色体引入了新的基因，突破了当前搜索的限制，更有利于算法寻找到全局最优解。

2.算法步骤

2.1编码和解码

        首先：为什么要编码，这里我们为了后续操作的方便，（包括上面概念提到的交叉和变异）所以我们要将实际问题用01字符串表示出来。在前面提到的个体，在计算机程序中就被编码为一个向量表示。

二进制编码：

        二进制编码通俗的将就是将我们的自变量从十进制映射到N位的二进制，而N取决于我们要求的精度。N越大精度越高。例如求解精度为 e=0.02，那么我们需要将x的区间[-10 10]，切分成(10−(−10))/0.02=1000 份。
又因为采用二进制编码所以实际需要的编码位数为：

                                                        2^9=512<1000<2^+=1024

当我们需要精度为0.02时，采用二进制编码最少需要10位数 ，那么实际的求解精度为

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        \mathrm{e}=20/1024\approx0.01953

        生物的DNA有四种碱基对，分别是ACGT，DNA的编码可以看作是DNA上碱基对的不同排列，不同的排列使得基因的表现出来的性状也不同（如单眼皮双眼皮）。在计算机中，我们可以模仿这种编码，但是碱基对的种类只有两种，分别是0，1。只要我们能够将不同的实数表示成不同的0，1二进制串表示就完成了编码。而编码后的二进制串就可以称为染色体。

        但是我们在这里并不关心如何得到二进制串，因为他可以通过随机函数生成。这也和自然选择的规律相似，我们无从得知开始的随机生物性态，但我们可以通过后续的自然选择来得到可行解。

  1. #pop表示种群矩阵，一行表示一个二进制编码表示的DNA，矩阵的行数为种群数目,DNA_SIZE为编码长度，不理解乘2的看后文
  2. pop = np.random.randint(2, size=(POP_SIZE, DNA_SIZE*2)) #matrix (POP_SIZE, DNA_SIZE*2)

二进制解码：

                其实很简单，假设现在有一个染色体基因为0101101011，那么他按权展开的到下面的式子：

        [0*2^9+1*2^8+0*2^7+1*2^6+1*2^5+0*2^4+1*2^3+0*2^2+1*2^0]

然后我们将其压缩到[0,1]区间内---需要根据字符串长度进行压缩。

        这里我们用上式除(2^{10}-1)就可以将其进行归一化。

        接着我们可以根据所需要的变量的范围将归一化的数映射到该区间内。

  1. #X_BOUND,Y_BOUND是x，y的取值范围 X_BOUND = [-3, 3], Y_BOUND = [-3, 3],
  2. x_ = num * (X_BOUND[1] - X_BOUND[0]) + X_BOUND[0] #映射为x范围内的数
  3. y_ = num * (Y_BOUND[1] - Y_BOUND[0]) + Y_BOUND[0] #映射为y范围内的数

2.2 初始化种群

                随机生成一组可行解，也就是第一代染色体。

2.3 适应度和选择

               我们已经得到了一个种群，现在要根据适者生存规则把优秀的个体保存下来，同时淘汰掉那些不适应环境的个体。现在摆在我们面前的问题是如何评价一个个体对环境的适应度？适应度由·适应度函数求得，这时个体就会因为适应度不同产生不同的适应度分数。

最大值的适应度函数：

  1. def get_fitness(pop): 
  2.     x,y = translateDNA(pop)
  3. 	pred = F(x, y)
  4. 	return (pred - np.min(pred)) + 1e-3 #减去最小的适应度是为了防止适应度出现负数，通过这一步fitness的范围为[0, np.max(pred)-np.min(pred)],最后在加上一个很小的数防止出现为0的适应度

最小值的适应度函数 :

  1. def get_fitness(pop): 
  2. 	x,y = translateDNA(pop)
  3. 	pred = F(x, y)
  4. 	return -(pred - np.max(pred)) + 1e-3

接着我们就要通过上面提到的轮盘赌方式对其进行选择。 

遗传算法依据原则：适应度越高，被选择的机会越高，而适应度低的，被选择的机会就低。

2.4 交叉和变异

        两个步骤就是使到子代不同于父代的根本原因（注意，不是优于！！！，只有经过自然的选择后，才会出现子代优于父代的倾向)。

        需要说明的是交叉和变异不是必然发生，而是有一定概率发生。先考虑交叉，最坏情况，交叉产生的子代的DNA都比父代要差（这样算法有可能朝着优化的反方向进行，不收敛），如果交叉是有一定概率不发生，那么就能保证子代有一部分基因和当前这一代基因水平一样；而变异本质上是让算法跳出局部最优解，如果变异时常发生，或发生概率太大，那么算法到了最优解时还会不稳定。交叉概率，范围一般是0.6~1，突变常数（又称为变异概率），通常是0.1或者更小。

  1. def crossover_and_mutation(pop, CROSSOVER_RATE = 0.8):
  2. 	new_pop = []
  3. 	for father in pop:		#遍历种群中的每一个个体，将该个体作为父亲
  4. 		child = father		#孩子先得到父亲的全部基因（这里我把一串二进制串的那些0，1称为基因）
  5. 		if np.random.rand() < CROSSOVER_RATE:			#产生子代时不是必然发生交叉，而是以一定的概率发生交叉
  6. 			mother = pop[np.random.randint(POP_SIZE)]	#再种群中选择另一个个体，并将该个体作为母亲
  7. 			cross_points = np.random.randint(low=0, high=DNA_SIZE*2)	#随机产生交叉的点
  8. 			child[cross_points:] = mother[cross_points:]		#孩子得到位于交叉点后的母亲的基因
  9. 		mutation(child)	#每个后代有一定的机率发生变异
  10. 		new_pop.append(child)
  11.  
  12. 	return new_pop
  13.  
  14. def mutation(child, MUTATION_RATE=0.003):
  15. 	if np.random.rand() < MUTATION_RATE: 				#以MUTATION_RATE的概率进行变异
  16. 		mutate_point = np.random.randint(0, DNA_SIZE)	#随机产生一个实数，代表要变异基因的位置
  17. 		child[mutate_point] = child[mutate_point]^1 	#将变异点的二进制为反转

2.5 算法终止 

一般来说有如下几个终止条件

  1. 在进行 X 次迭代之后，总体没有什么太大改变。
  2. 我们事先为算法定义好了进化的次数。
  3. 当我们的适应度函数已经达到了预先定义的值。

2.6 算法流程图

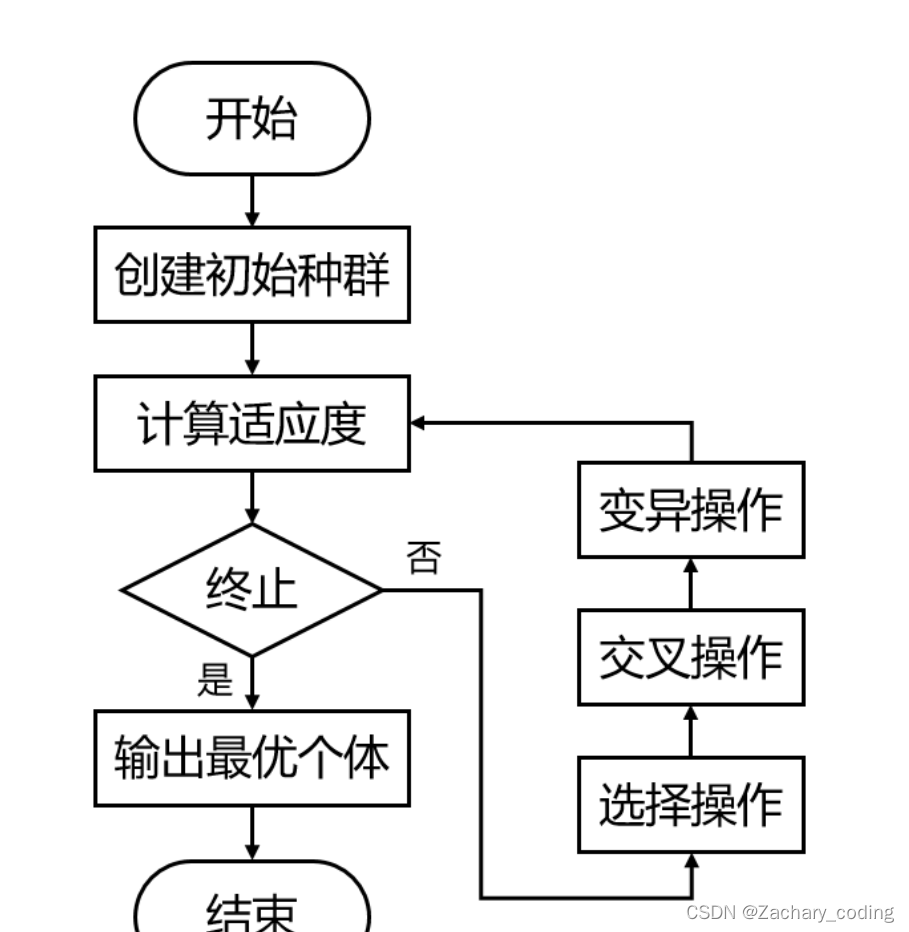
3.应用场景 

1）函数优化
函数优化是遗传算法的经典应用领域，也是遗传算法进行性能评价的常用算例。尤其是对非线性、多模型、多目标的函数优化问题，采用其他优化方法较难求解，而遗传算法却可以得到较好的结果。
（2）组合优化。
随着问题的增大，组合优化问题的搜索空间也急剧扩大，采用传统的优化方法很难得到最优解。遗传算法是寻求这种满意解的最佳工具。例如，遗传算法已经在求解旅行商问题、背包问题、装箱问题、图形划分问题等方面得到成功的应用.
（3）生产调度问题
在很多情况下，采用建立数学模型的方法难以对生产调度问题进行精确求解。在现实生产中多采用一些经验进行调度。遗传算法是解决复杂调度问题的有效工具，在单件生产车间调度、流水线生产车间调度、生产规划、任务分配等方面遗传算法都得到了有效的应用。
（4）自动控制。
在自动控制领域中有很多与优化相关的问题需要求解，遗传算法已经在其中得到了初步的应用。例如，利用遗传算法进行控制器参数的优化、基于遗传算法的模糊控制规则的学习、基于遗传算法的参数辨识、基于遗传算法的神经网络结构的优化和权值学习等。
（5）机器人
例如，遗传算法已经在移动机器人路径规划、关节机器人运动轨迹规划、机器人结构优化和行为协调等方面得到研究和应用。
（6）图像处理
遗传算法可用于图像处理过程中的扫描、特征提取、图像分割等的优化计算。目前遗传算法已经在模式识别、图像恢复、图像边缘特征提取等方面得到了应用。

4.遗传算法的基本特征

（1）智能式搜索
遗传算法的搜索策略，既不是盲目式的乱搜索，也不是穷举式的全面搜索，它是有指导的搜索。指导遗传算法执行搜索的依据是适应度，也就是它的目标函数。利用适应度，使遗传算法逐步逼近目标值。
（2）渐进式优化
遗传算法利用复制、交换、突变等操作，使新一代的结果优越于旧一代，通过不断迭代，逐渐得出最优的结果，它是一种反复迭代的过程。
（3）全局最优解
遗传算法由于采用交换、突变等操作，产生新的个体，扩大了搜索范围，使得搜索得到的优化结果是全局最优解而不是局部最优解。
（4）黑箱式结构
遗传算法根据所解决问题的特性，进行编码和选择适应度。一旦完成字符串和适应度的表达，其余的复制、交换、突变等操作都可按常规手续执行。个体的编码如同输入，适应度如同输出。因此遗传算法从某种意义上讲是一种只考虑输入与输出关系的黑箱问题。
（5）通用性强
传统的优化算法，需要将所解决的问题用数学式子表示，常常要求解该数学函数的一阶导数或二阶导数。采用遗传算法，只用编码及适应度表示问题，并不要求明确的数学方程及导数表达式。因此，遗传算法通用性强，可应用于离散问题及函数关系不明确的复杂问题，有人称遗传算法是一种框架型算法，它只有一些简单的原则要求，在实施过程中可以赋予更多的含义。
（6）并行式算法
遗传算法是从初始群体出发，经过复制、交换、突变等操作，产生一组新的群体。每次迭代计算，都是针对一组个体同时进行，而不是针对某个个体进行。因此，尽管遗传算法是一种搜索算法，但是由于采用这种并行机理，搜索速度很高。这种并行式计算是遗传算法的一个

重要特征。

5.代码实现 

  1.  
  2. import numpy as np
  3. import matplotlib.pyplot as plt
  4. from matplotlib import cm
  5. from mpl_toolkits.mplot3d import Axes3D
  6.  
  7. DNA_SIZE = 24
  8. POP_SIZE = 200
  9. CROSSOVER_RATE = 0.8
  10. MUTATION_RATE = 0.005
  11. N_GENERATIONS = 50
  12. X_BOUND = [-3, 3]
  13. Y_BOUND = [-3, 3]
  14.  
  15.  
  16. def F(x, y):
  17. 	return 3*(1-x)**2*np.exp(-(x**2)-(y+1)**2)- 10*(x/5 - x**3 - y**5)*np.exp(-x**2-y**2)- 1/3**np.exp(-(x+1)**2 - y**2)
  18.  
  19. def plot_3d(ax):
  20.  
  21. 	X = np.linspace(*X_BOUND, 100)
  22. 	Y = np.linspace(*Y_BOUND, 100)
  23. 	X,Y = np.meshgrid(X, Y)
  24. 	Z = F(X, Y)
  25. 	ax.plot_surface(X,Y,Z,rstride=1,cstride=1,cmap=cm.coolwarm)
  26. 	ax.set_zlim(-10,10)
  27. 	ax.set_xlabel('x')
  28. 	ax.set_ylabel('y')
  29. 	ax.set_zlabel('z')
  30. 	plt.pause(3)
  31. 	plt.show()
  32.  
  33.  
  34. def get_fitness(pop): 
  35.     x,y = translateDNA(pop)
  36. 	pred = F(x, y)
  37. 	return (pred - np.min(pred)) + 1e-3 #减去最小的适应度是为了防止适应度出现负数，通过这一步fitness的范围为[0, np.max(pred)-np.min(pred)],最后在加上一个很小的数防止出现为0的适应度
  38.  
  39.  
  40. def translateDNA(pop): #pop表示种群矩阵，一行表示一个二进制编码表示的DNA，矩阵的行数为种群数目
  41. 	x_pop = pop[:,1::2]#奇数列表示X
  42. 	y_pop = pop[:,::2] #偶数列表示y
  43. 	
  44. 	#pop:(POP_SIZE,DNA_SIZE)*(DNA_SIZE,1) --> (POP_SIZE,1)
  45. 	x = x_pop.dot(2**np.arange(DNA_SIZE)[::-1])/float(2**DNA_SIZE-1)*(X_BOUND[1]-X_BOUND[0])+X_BOUND[0]
  46. 	y = y_pop.dot(2**np.arange(DNA_SIZE)[::-1])/float(2**DNA_SIZE-1)*(Y_BOUND[1]-Y_BOUND[0])+Y_BOUND[0]
  47. 	return x,y
  48.  
  49. def crossover_and_mutation(pop, CROSSOVER_RATE = 0.8):
  50. 	new_pop = []
  51. 	for father in pop:		#遍历种群中的每一个个体，将该个体作为父亲
  52. 		child = father		#孩子先得到父亲的全部基因（这里我把一串二进制串的那些0，1称为基因）
  53. 		if np.random.rand() < CROSSOVER_RATE:			#产生子代时不是必然发生交叉，而是以一定的概率发生交叉
  54. 			mother = pop[np.random.randint(POP_SIZE)]	#再种群中选择另一个个体，并将该个体作为母亲
  55. 			cross_points = np.random.randint(low=0, high=DNA_SIZE*2)	#随机产生交叉的点
  56. 			child[cross_points:] = mother[cross_points:]		#孩子得到位于交叉点后的母亲的基因
  57. 		mutation(child)	#每个后代有一定的机率发生变异
  58. 		new_pop.append(child)
  59.  
  60. 	return new_pop
  61.  
  62. def mutation(child, MUTATION_RATE=0.003):
  63. 	if np.random.rand() < MUTATION_RATE: 				#以MUTATION_RATE的概率进行变异
  64. 		mutate_point = np.random.randint(0, DNA_SIZE*2)	#随机产生一个实数，代表要变异基因的位置
  65. 		child[mutate_point] = child[mutate_point]^1 	#将变异点的二进制为反转
  66.  
  67. def select(pop, fitness):    # nature selection wrt pop's fitness
  68.     idx = np.random.choice(np.arange(POP_SIZE), size=POP_SIZE, replace=True,
  69.                            p=(fitness)/(fitness.sum()) )
  70.     return pop[idx]
  71.  
  72. def print_info(pop):
  73. 	fitness = get_fitness(pop)
  74. 	max_fitness_index = np.argmax(fitness)
  75. 	print("max_fitness:", fitness[max_fitness_index])
  76. 	x,y = translateDNA(pop)
  77. 	print("最优的基因型：", pop[max_fitness_index])
  78. 	print("(x, y):", (x[max_fitness_index], y[max_fitness_index]))
  79.  
  80.  
  81. if __name__ == "__main__":
  82. 	fig = plt.figure()
  83. 	ax = Axes3D(fig)	
  84. 	plt.ion()#将画图模式改为交互模式，程序遇到plt.show不会暂停，而是继续执行
  85. 	plot_3d(ax)
  86.  
  87. 	pop = np.random.randint(2, size=(POP_SIZE, DNA_SIZE*2)) #matrix (POP_SIZE, DNA_SIZE)
  88. 	for _ in range(N_GENERATIONS):#迭代N代
  89. 		x,y = translateDNA(pop)
  90. 		if 'sca' in locals(): 
  91. 			sca.remove()
  92. 		sca = ax.scatter(x, y, F(x,y), c='black', marker='o');plt.show();plt.pause(0.1)
  93. 		pop = np.array(crossover_and_mutation(pop, CROSSOVER_RATE))
  94. 		#F_values = F(translateDNA(pop)[0], translateDNA(pop)[1])#x, y --> Z matrix
  95. 		fitness = get_fitness(pop)
  96. 		pop = select(pop, fitness) #选择生成新的种群
  97. 	
  98. 	print_info(pop)
  99. 	plt.ioff()
  100. 	plot_3d(ax)


 

参考博客:遗传算法详解 附python代码实现_遗传算法python-CSDN博客

一文读懂遗传算法工作原理（附Python实现） - 知乎 (zhihu.com)

10分钟搞懂遗传算法(含源码) - 知乎 (zhihu.com)

 遗传算法python（含例程代码与详解)_python遗传算法-CSDN博客

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/从前慢现在也慢/article/detail/207807
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号