非线性优化--NLopt原理介绍及使用方法

前言

什么是NLopt ？
NLopt(nonlinear optimization)是一个免费的开源的库，提供了很多种非线性优化算的使用接口。

NLopt的优点：
1、其中非常大的优势就是提供多种支持的语言，包括C/ C++/ Julia/ Python/ R/ Fortran/ Lua/ OCaml/ Octave等都支持
2、它还可以让你对一个问题尝试不同的算法，调整一个参数就行
3、支持一些高维的问题，比如可以做非常多的参数的优化，可以做非常多的约束的优化。
4、支持全局优化和局部优化
5、支持常见的需要导数和不需要导数的多种算法
6、支持等式、不等式、有界等不同的约束极值问题

NLopt支持的算法可以从这查询，

非线性优化

既然NLopt是解决非线性优化的问题，那么先说明下什么是非线性优化。

通俗一点来说 非线性优化就是求函数的极值。我们想求一个 函数的极值问题的时候，线性函数是最简单的，因为是线性的嘛，单调增或者单调减，那么找到边界就可以求到极值。例如 f(x)=ax+b。
简单的非线性函数也是很容易求得极值的，例如f(x)=x*x.可以通过求导得到极值点，然后求得其极值。

但是对于复杂的非线性函数，或者复杂的数学模型，求导很困难或者无法求导的时候怎么求极值呢？那么就出现了很多非线性优化的算法。来解决对于复杂数学模型的求极值的问题。

再多说一句，在非线性优化里面通常求最小值，如果你求最大值就是在优化前给函数加个负号的事情。

NLopt官网的图片也很直观

这个小红点就是极值点，需要优化的最终结果。

NLopt中的几个概念

1 优化问题的数学模型

对于一个非线性优化问题的数学模型包裹以下几个概念：

1）NLopt解决了以下形式的一般非线性优化问题

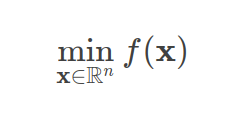
其中 f 是目标函数，x表示n个 优化参数（也称为设计变量或决策参数）。

就是上面通俗的解释非线性优化问题的数学表达

** 2）边界约束**
此问题可以有选择地受到边界约束（也称为box约束）
也就是求极值时参数的范围，数学表达如下：

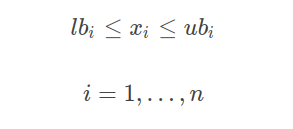
给定下限lb和上限ub（对于部分或完全无约束的问题分别为-∞和/或+∞）

3)非线性不等式约束
一个参数也可以选择具有m个非线性不等式约束（有时称为非线性规划问题）：

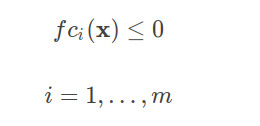
4)非线性等式约束
一些NLopt算法还支持p个非线性等式约束:

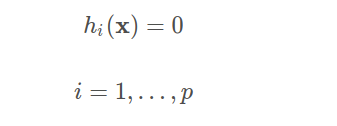
满足所有边界约束、不等式和等式约束的点x称为可行点，所有可行点的集合为可行区域

举个例子

min（sinx1+cosx2） ----目标函数
其中 x1，x2 ----优化参数
2<x1<10 1<x2<3 ----边界约束
x1*x1-sin(x2)>0 ----非线性不等式约束
x1+x2=1 ----非线性等式约束(虽然这是个线性的，就这么招把)

2 全局优化与局部优化

全局优化的英文是（global optimization）
局部优化的英文是（local optimization）
记住这个对与了解代码有帮助

NLopt包含对目标函数进行全局或局部优化的算法。

那么什么是全局优化和局部优化呢 ，概念也不难理解

全局优化

全局优化是找到在整个可行区域内使目标函数 最小的 可行点x的问题。
通俗来说就是从所有可能的x值里面找到最小值

通常，可能是一个非常困难的问题，随着参数数量的增加，难度将成倍增加。比如上面的例子是x1和x2两个参数，有着不同的组合方式。那么如何有x1~x100个参数呢，会有多少种组合方式呢？

实际上，除非知道有关 f 的特殊信息，否则甚至无法确定是否找到了真正的全局最优值，因为可能会出现 f 值的突然下降，且这个值隐藏在您尚未查找的参数空间中。

NLopt包含几种全局优化算法，如果维度n不太大，可以很好且合理地处理优化问题

局部优化

局部优化是一个容易得多的问题。
它的目标是找到一个仅是局部最小值的可行点x：f（x）小于或等于所有附近可行点的f值
通常，非线性优化问题可能有很多局部最小值，算法确定的最小值位置通常取决于用户提供给算法的起点。
另一方面，即使在非常高维的问题中（尤其是使用基于梯度的算法），局部优化算法通常也可以快速定位局部最小值。

基于梯度（Gradient）算法与无导数算法

这个是非线性算法求解时候的分类了，梯度就是导数的意思。
梯度英文Gradient ，记住。在代码中很多函数的形参 名叫grad就是梯度的意思

梯度算法

梯度按通俗的意思来讲就是 参数x变化的方向和大小

对于局部优化最高效的算法通常要求用户提供梯度

可以使用很少的额外计算量，在计算f的值同时计算梯

梯度怎么求得呢，一般通过 计算导数的方法来计算梯度。例如 min（lnx1-lnx2），x1的梯度就是1/x1，x2的梯度就是-1/x2.
那么不是因为导数不好求，才需要这些优化算法吗，怎么又求导呢？还有其它方法来求梯度

基于梯度的方法对于非常高维的参数空间的有效优化至关重要

无导数算法

上面说了计算梯度有的时候是很困难的。那么有的优化模型在不使用的梯度的时候可以求解出来，就有了无导数算法。

该算法仅要求用户提供给定点x的函数值 f(x)。

这种方法通常必须对f进行至少几倍n点的计算。n就是x的个数。当x的个数不是很多的时候，可以使用这种方法。不用求梯度了就。

终止条件

就是计算的时候什么情况下停下。 算法都是通过迭代的方式不断计算下去，通过比较得到优化的点。那么什么时候停止呢？

在理想情况下，当发现最佳值在某个所需的公差范围内时，算法应停止运行。
但是怎么可能提前知道最优值呢，算法求的不就是最优值吗，所以这种理想情况的停止是不可行的

实际使用的时候会通过对解决方案中的误差使用启发式估计。NLopt也提供了不同的终止条件选择，有以下几个。

函数值容差和参数容差

在函数的计算值上指定 分数容差（ftol_rel）和绝对容差（ftol_abs） 当 df/f<ftol_rel 或者 df<ftol_abs 时停止

同样可以在参数x上指定 分数容差（xtol_rel）和绝对容差（xtol_abs） 当 dx/x<xol_rel 或者 dx<xtol_abs 时停止

通常情况下，分数容差会更有用，因为它独立于任何绝对比例因子或单位

当你认为 函数最小值或 参数最优点在0附近时，那么绝对容差时有用的

函数值停止数值

另外一种NLopt提供的停止方法是可以通过设定优化达到的函数值为一个固定值时，优化停止

这种停止方法对于 comparing algorithms （一种非线性优化算法）更有效果。在长时间运行一种算法以找到所需精度的最小值后，您可以询问算法需要多少次迭代才能获得相同精度或更高精度的最优值。

迭代次数和时间

最后，可以设置最大的迭代次数，或者计算时间，来控制优化的停止。

如果想确保算法在规定的时间内计算出结果，
这两个终止条件非常有用，
虽然它不是绝对最优的。

也是控制全局优化的有用方法。

对于全局优化的停止

在决定什么时候停止对全局的优化是一件困难的事情。因为没有办法确定真的取得了最小值，或者接近最小值了。

所有在决定什么时候停止全局优化的条件 设为控制优化的时间。

另一种策略是从较短的运行时间开始，然后反复将运行时间加倍，直到返回值不再变化。

建议不要使用函数值容差和参数容差在全局优化中

对于MLSL算法，需要设置局部优化算法的ftol和xtol参数来控制局部搜索的容差，而不是全局搜索的容差。

安装库

下载 nlopt v2.6.2 链接地址

然后就是安装，NLopt 的安装 就是linux上标准的安装方式，很简单。有C编译器就行。

在nlopt文件的目录下面有CMakeLists.txt 文件 标准的CMake安装系统，通过下面指令安装

mkdir build
cd build
cmake ..
make
1
2
3
4

然后回到nlopt路径下面， 安装 NLopt libraries 和 header files

默认的话，在 /usr/local/lib 路径下 会生成 libnlopt.so
/usr/local/include 路径下 会生成 nlopt.h

在使用的时候包含其头文件

#include <nlopt.hpp>
1

NLopt使用方法

通过 对 一个 数学 模型 的求解 来介绍 NLopt的使用方法

数学模型：

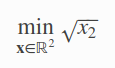
这个是目标函数 求满足 条件的情况下 x2的开平方最小

边界约束

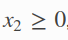
非线性不等式约束如下

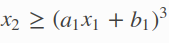
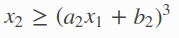
有两个参数 x1 和 x2 ，其中 a和b是模型的参数可以设为任意的固定值，这个模型设为a1=2，b1=0，a2=-1，b2=1

绘制这两条曲线 如下图

可行性区域在交汇的上方，最优点在交汇处，最优值大约为0.5443

下面通过NLopt的方式来求解这个数学模型。

通过图片上的曲线可以看出，x2>0的约束没有什么用，因为可行性区域的都在0之上
但是在使用NLopt的时候最好也把这个条件加上去。

在使用NLopt的时候，基本要包含两个头文件

#include <math.h>
#include <nlopt.h>
1
2

然后定义目标函数 根据上面的数学模型 的 目标函数来

double myfunc(unsigned n, const double *x, double *grad, void *my_func_data)
{
    if (grad) {
        grad[0] = 0.0;
        grad[1] = 0.5 / sqrt(x[1]);
    }
    return sqrt(x[1]);
}
1
2
3
4
5
6
7
8

myfunc时定义的函数的名字可以随意改，后面的参数基本不要动，就是这么个形式的

其中n代表待优化的因子个数

x是待优化的参数向量

grad 是梯度，对于基于梯度的算法，则在目标函数里面需要给grad赋值， grad[0]附值对应x[0]的偏导数，grad[1]附值对应x[1]的偏导数。对于无导数算法的，不需要计算导数，grad应该是NULL。

my_func_data 是外部参数用于数学模型中的，如果没有，就不用。

返回值要是 你的 目标函数

非线性不等式约束
对于前面的模型，不等式约束相当于参数不同的一样的约束方程，只是a1、a2的值不同罢了，所以可以写成一个不等式约束，然后用传入外部参数的方式实现。【上面的目标函数要是需要传入参数，也是这么个方法】

对于每个不等式约束我们需要传入a和b的值，创建一个结构体

typedef struct {
    double a, b;
} my_constraint_data;
1
2
3

之后定义 非线性不等式约束
对于这个一定把 不等式先变成 不等函数 <0的情况 这样求导的符号才对
定义函数如下：

double myconstraint(unsigned n, const double *x, double *grad, void *data)
{
	//声明对应外部数据刚定义的结构体 数据 然后赋值就可以了
    my_constraint_data *d = (my_constraint_data *) data;
    //获得a和b
    double a = d->a, b = d->b;
    if (grad) {
        grad[0] = 3 * a * (a*x[0] + b) * (a*x[0] + b);//对x0求偏导
        grad[1] = -1.0;//对x1求偏导
    }
    return ((a*x[0] + b) * (a*x[0] + b) * (a*x[0] + b) - x[1]);//返回 不等函数
 }
1
2
3
4
5
6
7
8
9
10
11
12

函数的形参和目标函数一致，代表的意思也一致，就不描述了。

完成了数学模型的 目标函数定义、不等式约束、等式约束（上面的数学模型没有）可以开始优化了

首先创建 nlopt_opt 类的 对象，然后附各种参数

nlopt_opt opt;//  **nlopt_opt**  类的 对象
1

然后附各种参数

opt = nlopt_create(NLOPT_LD_MMA, 2);//设置算法和维度
1

设置算法和维度 算法有很多种选择 ， 维度就是 x的个数，优化因子个数

double lb[2] = { -HUGE_VAL, 0 }; //声明x的下限  第0个元素代表x[0]  第1个元素代表x[1]
nlopt_set_lower_bounds(opt, lb);//设置x的下限
1
2

声明x的下限 第0个元素代表x[0] 第1个元素代表x[1]
设置x的下限
因为数学模型里面没有上限，可以不设置，默认为无穷大
如果需要设置的话 和 下限基本一致

double lb[2] = { 5, 10 }; //声明x的上限  第0个元素代表x[0]  第1个元素代表x[1]
nlopt_set_upper_bounds(opt, lb);//设置x的上限
1
2

nlopt_set_min_objective(opt, myfunc, NULL);//设置目标函数
1

设置目标函数 ，第二个参数就是上面定义的目标函数的函数名，第三个参数是外部参数，因为没有，则为NULL

my_constraint_data data[2] = { {2,0}, {-1,1} };//不等式的外部参数  上面定义的结构体
nlopt_add_inequality_constraint(opt, myconstraint, &data[0], 1e-8);//不等式约束1
nlopt_add_inequality_constraint(opt, myconstraint, &data[1], 1e-8);//不等式约束1
1
2
3

添加不等式约束

第二个参数是不等式约束的函数名
第三个参数是外部参数
第四个参数1e-8是很重要的，叫做约束的容差，如果一个点满足，不等函数>-(1e-8)那这个点也不采用。这样做是出于收敛的目的，避免微小的偏差导致不能收敛

为了收敛，还需要设置几个停止的标准，就是上面提到的终止条件

nlopt_set_xtol_rel(opt, 1e-4);//设置x的绝对容差
1

设置x的绝对容差

还有很多其它的参数可以配置你的优化，可以参考这里

然后就是调用 nlopt_optimize()函数执行优化了
可以设置初始值

double x[2] = { 1.234, 5.678 };  /* x的初始值 */
double minf; /* 计算的最小值存入的变量 */
if (nlopt_optimize(opt, x, &minf) < 0) {
    printf("nlopt failed!\n");
}
else {
    printf("found minimum at f(%g,%g) = %0.10g\n", x[0], x[1], minf);
}
1
2
3
4
5
6
7
8

如果优化失败，nlopt_optimize函数会返回负值
失败的原因一般是 传递无效参数、内存不足或类似情况

最后可以调用 nlopt_destroy 来结束优化

nlopt_destroy(opt);
1

如果想要知道迭代次数，那么可以在定义的目标函数里面加入一个自增1的变量

int count = 0;
double myfunc(int n, const double *x, double *grad, void *my_func_data)
{
    ++count;
    if (grad) {
        grad[0] = 0.0;
        grad[1] = 0.5 / sqrt(x[1]);
    }
    return sqrt(x[1]);
}
1
2
3
4
5
6
7
8
9
10