多维灰色GM(1,N)预测模型及MATLAB实现_gm(1,n)模型matlab代码

这篇文章主要记录一下基本的GM(1,N)预测模型的概念、公式推导以及MATLAB代码实现，如有问题欢迎指正交流。
之前做毕设时在CSDN上看过关于GM(1,N)预测模型的代码，但是都几乎是同样的代码同样的问题，在第二个预测值上出现了预测值为0的畸变，所以我自己对程序进行了一点修改，解决了之前遇到的问题。
在对灰色GM(1,1)模型有了一定了解后，可以发现其主要针对线性数据具有较好的预测效果，并且在预测时只考虑了自变量本身的影响，而没有考虑其他外界影响因素对预测结果的影响作用，因此有了多维灰色预测模型GM(1,N)，其中N表示考虑的相关因素维度。
GM(1,N)模型的预测原理与GM(1,1)类似，不同之处在于输入数据变量是n个。
GM(1,N)模型的建模过程如下：
设系统有特征数据序列：

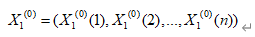
相关因素序列：

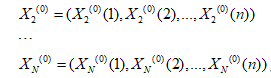
令 （i=1,2,…,N）的1-AGO序列为Xi（1），其中

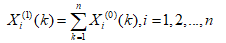
生成 的紧邻均值数列：

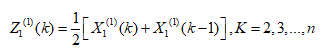
根据灰色理论对 建立微分方程GM（1,n）：

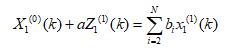
其中，a称为发展系数， 称为驱动系数， 称为驱动项。
引入矩阵向量记号：

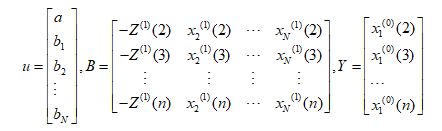
采用最小二乘法可求得u：

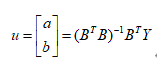
当 （i=1,2,…,N）变化幅度较小时，可得：

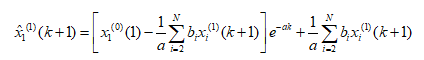
解得还原值：

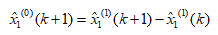
MATLAB实现：

A=input('请输入原始特征序列：');
x0=input('请输入相关因素序列：');
M=input('请输入预测步长：');
N=1;
while N<=M
[n,m]=size(x0);
AGO=cumsum(A);
T=1;
x1=zeros(n,m+T);

for k=2:m
    Z1(k)=(AGO(k)+AGO(k-1))*0.5; %Z(i)为xi(1)的紧邻均值生成序列
end
for i=1:n
    for j=1:m
        for k=1:j
            x1(i,j)=x1(i,j)+x0(i,k);%原始数据一次累加,得到xi(1)
        end
    end
end
x11=x1(:,1:m);
X=x1(:,2:m)';%截取矩阵
Yn =A;%Yn为常数项向量
Yn(1)=[]; %从第二个数开始，即x(2),x(3)...
Yn=Yn';
%Yn=A(:,2:m)';
Z=Z1(:,2:m)';
B=[-Z,X];
C=(inv(B'*B))*B'*Yn;%由公式建立GM(1,n)模型
a=C(1);
C1=C';
b=C1(:,2:n+1);
F=[];
F(1)=A(1);
u=zeros(1,m);
for i=1:m
       for j=1:n
        u(i)=u(i)+(b(j)*x11(j,i));
       end
end
for k=2:m
    F(k)=(A(1)-u(k)/a)*exp(-a*(k-1))+u(k)/a;
end
G=[];
G(1)=A(1);
for k=2:m
G(k)=F(k)-F(k-1);%两者做差还原原序列，得到预测数据
end

%对下一刻进行预测
x0_y=input('请输入下一刻相关因素序列：');
U=[];
U(1)=0;
for k=1
for j=1:n
U(k)=U(k)+(b(j)*(x11(j,m)+x0_y(j)));
end
end
F_y=[];
F_y(1)=0;
for k=1
 F_y(k)=(A(1)-U(k)/a)*exp(-a*m)+U(k)/a;
end
 G_y=zeros(1,M);
 
for k=1
 G_y(N)=F_y(k)-F(m);
end
N=N+1;

end

disp('GM(1,n)预测值：');
disp(G_y(N-1));

%绘图
t1=1:m;
t2=1:m;
plot(t1,A,'bo--');
hold on;
plot(t2,G,'r*-'); 
axis([1 m 0 0.4]);
title('瓦斯浓度预测结果');
legend('真实值','预测值'); 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84

程序最后一段绘制曲线图时，为了使图片更美观，根据我用的数据设置了一下坐标轴的范围，此处可根据需求自行调整。我用的数据不在这里公开了，就放一个预测结果图吧：

（用不同的数据进行试验得出的结果可能偏差大小也存在差异）
可以看出模拟效果不是很好哦，所以才会有后续各种对GM(1,N)模型的改进与优化方法，具体改进方法我在之后应该也会写出来的，算是记录一下自己对灰色模型研究学习的一个心路历程吧~