超详细讲解“二分查找”，你看不懂算我笨！_二分查找算法举例说明

二分查找有着查找速度快，平均性能好等优点，但仅当列表是有序的时候，二分查找才管用。面试比较常考，今天我们具体看一下二分查找。

---

0. 我们先从一个场景开始了解吧

有一天，小明心血来潮去图书馆借了N本书，结果出图书馆的时候，警报响了，于是门卫大爷把小明拦下，要检查一下哪本书没有登记出借。小明正准备把每一本书在报警器下过一下，以找出引发警报的书，但是大爷露出不屑的眼神：你连二分查找都不会吗？于是大爷把书分成两堆，让第一堆过一下报警器，报警器响；于是再把这堆书分成两堆…… 最终，检测了 logN 次之后，大爷成功的找到了那本引起警报的书，露出了得意和嘲讽的笑容。于是小明背着剩下的书走了，心想：大爷果然还是我大爷！

是不是觉得二分查找很简单？！其实思想是很简单，但是有不少细节需要注意。正如Knuth 大佬（发明 KMP 算法的那位）所说：
“
Although the basic idea of binary search is comparatively straightforward, the details can be surprisingly tricky…

大致意思就是：思路很简单，细节是魔鬼。

接下来我就带大家来分析需要注意的细节，以及二分查找的巧妙运用。

1. 基本的二分查找

根据二分查找的思想，我们将其数学化，符号和意义如下：
二分查找（前提条件：数组有序）
nums：查找数组
t：待查找目标元素
初始化 left = 0，左边界
right = nums.length -1，右边界
mid = （left + right）/ 2，查找的中间位置
查找区间 [left, right]：while(left <= right)
查找目标元素的位置，无则返回-1

算法方程可表示如下：

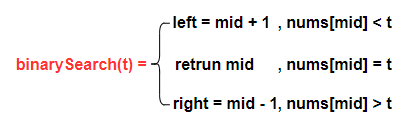
有了基本思路，我们废话少说，直接放码过来！

Java实现代码如下：

private int binarySearchWithR(int[] nums, int target) {
        int left = 0;
        int right = nums.length - 1; // 注意 [left, right]

        while(left <= right) { // 注意
            int mid = (right - left) / 2 + left; // mid = (left + right) / 2 的优化形式，防止溢出！
            if(nums[mid] == target)
                return mid;
            else if (nums[mid] < target)
                left = mid + 1;
            else if (nums[mid] > target)
                right = mid - 1; // 注意
        }
        return -1;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

需要注意的细节就是代码中注明的地方，其实这几个地方是相关的。
因为初始化 right = 数组的长度 - 1；即最后一个元素，是可以取到的。此时的查找区间为 [left,right]，所以决定了 while(left <= right)，判断条件是可以加等号的。同时也决定了后续的 right = mid - 1；需要减1，否则可能导致下标越界。
其实也可以初始化 right = 数组的长度；是不可以取到的。此时的查找区间为 [left,right)，所以决定了 while(left < right)，判断条件是不可以加等号的。同时也决定了后续的 right = mid；不需要减1。
不取右边界情况的代码如下：

private int binarySearchWithoutR(int[] nums, int target) {
        int left = 0;
        int right = nums.length; // 注意 [left, right)

        while(left < right) { // 注意
            int mid = (right - left) / 2 + left;
            if(nums[mid] == target)
                return mid;
            else if (nums[mid] < target)
                left = mid + 1;
            else if (nums[mid] > target)
                right = mid; // 注意
        }
        return -1;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

所以，明白了二分查找的思路，注意这些细节，也就不会导致各种情况的混乱。

为了更深入的理解二分查找的过程，下面将运行过程图形化（做这些图花了我一晚上，强迫症的我太不容易了T_T）

以下情况为初始化 right = 数组长度 - 1 ，查找区间为 [left, right]

2. 寻找左侧边界的二分查找

二分查找的巧妙运用一就是寻找一个数的左侧边界，如寻找 [1,2,4,4,5,6] 中，4 第一次出现的位置？也就是寻找 4 的左侧边界。

寻找左侧边界的二分查找（前提条件：数组有序）
nums：查找数组
t：待查找目标元素
初始化 left = 0，左边界
right = nums.length -1，右边界
mid = （left + right）/ 2，查找的中间位置
查找区间：while(left <= right)
查找目标元素第一次出现的位置（左侧边界），无则返回比它大的数的左侧边界

算法方程可表示如下：

Java实现

private int leftBound(int[] nums, int target) {
        int left = 0;
        int right = nums.length - 1;

        while (left <= right) {
            int mid = (right - left) / 2 + left;
            if (nums[mid] == target) {
                right = mid -1; // 注意
            } else if (nums[mid] < target) {
                left = mid + 1;
            } else if (nums[mid] > target) {
                right = mid -1;
            }
        }
        return left; // 注意
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

可以看出，此代码与二分查找唯一的不同就是注意的地方。当找到目标元素时，并不是直接返回，而是收紧右侧边界，继续查找，以锁定左侧边界。最后返回左侧边界

3. 寻找右侧边界的二分查找

同理，如寻找 [1,2,4,4,5,6] 中，4 最后一次出现的位置？也就是寻找 4 的右侧边界。

寻找右侧边界的二分查找（前提条件：数组有序）
nums：查找数组
t：待查找目标元素
初始化 left = 0，左边界
right = nums.length -1，右边界
mid = （left + right）/ 2，查找的中间位置
查找区间：while(left <= right)
查找目标元素最后一次出现的位置（右侧边界），无则返回比它小的数的右侧边界

算法方程可表示如下：

Java实现

private int rightBound(int[] nums, int target) {
        int left = 0, right = nums.length-1;

        while (left <= right) {
            int mid = (right - left) / 2 + left;
            if (nums[mid] == target) {
                left = mid + 1; // 注意
            } else if (nums[mid] < target) {
                left = mid + 1;
            } else if (nums[mid] > target) {
                right = mid - 1;
            }
        }
        return right; // 注意
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

可以看出，此代码与二分查找唯一的不同也是注意的地方。当找到目标元素时，并不是直接返回，而是收紧在侧边界，继续查找，以锁定右侧边界。最后返回右侧边界

4. 总结

第一个，最基本的二分查找算法：

因为我们初始化 right = nums.length - 1
所以决定了我们的「搜索区间」是 [left, right]
所以决定了 while (left <= right)
同时也决定了 left = mid+1 和 right = mid-1

因为我们只需找到一个 target 的索引即可
所以当 nums[mid] == target 时可以立即返回
1
2
3
4
5
6
7

第二个，寻找左侧边界的二分查找：

因为我们初始化 right = nums.length - 1
所以决定了我们的「搜索区间」是 [left, right]
所以决定了 while (left <= right)
同时也决定了 left = mid+1 和 right = mid-1

因为我们需找到 target 的最左侧索引
所以当 nums[mid] == target 时不要立即返回
而要收紧右侧边界以锁定左侧边界
1
2
3
4
5
6
7
8

第三个，寻找右侧边界的二分查找：

因为我们初始化 right = nums.length - 1
所以决定了我们的「搜索区间」是 [left, right]
所以决定了 while (left <= right)
同时也决定了 left = mid+1 和 right = mid-1

因为我们需找到 target 的最右侧索引
所以当 nums[mid] == target 时不要立即返回
而要收紧左侧边界以锁定右侧边界
1
2
3
4
5
6
7
8

如果以上内容你都能理解，那么恭喜你，二分查找算法的细节不过如此。

5. 最后我们来用一道LeetCode的算法题验收一下成果吧

牛客网链接
题目描述
统计一个数字在排序数组中出现的次数。
Input:
nums = 1, 2, 4, 4, 5, 6
K = 4

Output:
2

解题思路
我们可以找出目标值的左边界和右边界，然后用右边界 - 左边界 + 1 ，如 4 的左边界为 2，右边界为 3。但是这样左右边界的方法都要编写，有一个巧妙的方法，可以偷懒只写一个方法即可。

找出 4 的左边界1（或右边界1），再找出 4+1 的左边界2（或4 - 1的右边界2），用左边界2 - 左边界1 即可（或右边界2 - 右边界1）

我的解题代码： 已通过

// 根据二分查找的思路，修改为寻找一个数的左侧边界。
public class Solution {
    public int GetNumberOfK(int [] array , int k) {
       if(array == null || array.length == 0)    return 0;
       // 这个数第一次出现的位置（即左边界），无此值则返回比它大的数的左侧边界
       int first = myleft_bound(array, k);
        // 这个数最后一次出现的位置（用目标值+1的左边界），无此值则返回比它大的数的左侧边界
       int last = myleft_bound(array, k+1);
       return last - first;
    }
    
    // 寻找target的左侧边界，无则返回比它大的数的左侧边界
    private int myleft_bound(int[] nums, int target) {
        int left = 0;
        int right = nums.length - 1;

        while (left <= right) {
            int mid = (right - left) / 2 + left;
            if (nums[mid] == target) {
                // 关键！！！基本的二分查找若找到是返回下标
                //因为我们需找到 target 的最左侧索引
                //所以当 nums[mid] == target 时不要立即返回
                //而要收紧右侧边界以锁定左侧边界
                right = mid -1; 
            } else if (nums[mid] < target) {
                left = mid + 1;
            } else if (nums[mid] > target) {
                right = mid -1; 
            }
        }
        // 返回左侧边界
        return left;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

6. 参考

二分查找算法详解

---

以上。记录一下这次学习的二分查找，分享给大家顺便整理下思路。码字做图不易，若有帮助，点个赞鼓励一下鸭~