算法每日一题：美丽塔2 | 单调栈 | 动态规划 | 抛物线_美丽塔题解

今天的每日一题超级不简单哦！

题目：leetcode 2866
给你一个长度为 n 下标从 0 开始的整数数组 maxHeights 。
你的任务是在坐标轴上建 n 座塔。第 i 座塔的下标为 i ，高度为 heights[i] 。
如果以下条件满足，我们称这些塔是 美丽 的：

1. 1 <= heights[i] <= maxHeights[i]
2. heights 是一个 山脉 数组。

如果存在下标 i 满足以下条件，那么我们称数组 heights 是一个 山脉 数组：

• 对于所有 0 < j <= i ，都有 heights[j - 1] <= heights[j]
• 对于所有 i <= k < n - 1 ，都有 heights[k + 1] <= heights[k]

请你返回满足 美丽塔 要求的方案中，高度和的最大值 。
示例：
示例 1：

输入：maxHeights = [5,3,4,1,1]
输出：13
解释：和最大的美丽塔方案为 heights = [5,3,3,1,1] ，这是一个美丽塔方案，因为：
- 1 <= heights[i] <= maxHeights[i]  
- heights 是个山脉数组，峰值在 i = 0 处。
13 是所有美丽塔方案中的最大高度和。
1
2
3
4
5
6

示例 2：

输入：maxHeights = [6,5,3,9,2,7]
输出：22
解释： 和最大的美丽塔方案为 heights = [3,3,3,9,2,2] ，这是一个美丽塔方案，因为：
- 1 <= heights[i] <= maxHeights[i]
- heights 是个山脉数组，峰值在 i = 3 处。
22 是所有美丽塔方案中的最大高度和。
1
2
3
4
5
6

示例 3：

输入：maxHeights = [3,2,5,5,2,3]
输出：18
解释：和最大的美丽塔方案为 heights = [2,2,5,5,2,2] ，这是一个美丽塔方案，因为：
- 1 <= heights[i] <= maxHeights[i]
- heights 是个山脉数组，最大值在 i = 2 处。
注意，在这个方案中，i = 3 也是一个峰值。
18 是所有美丽塔方案中的最大高度和。
1
2
3
4
5
6
7

提示：

• 1 <= n == maxHeights <= 105
• 1 <= maxHeights[i] <= 109

分析：
首先，分析问题：
这道题是说，给了我们一个 maxHeights 数组，然后让我们在maxHeights数组中寻找一个每个对应元素的值不超过它的元素值的一个数组，这个数组的元素特征是：只有一个最大值的抛物线，然后这个抛物线的元素 和** **是所有抛物线情况里元素和最大的，

好，问题我们理解了我们继续分析：
我们很容易可以推断出来，只要确定最大值是什么，我们就可以构造出一个抛物线（使最大值的左边的所有值比它小，最大值右边的所有值比它大，如图所示，红线下方的即为max值的和区域）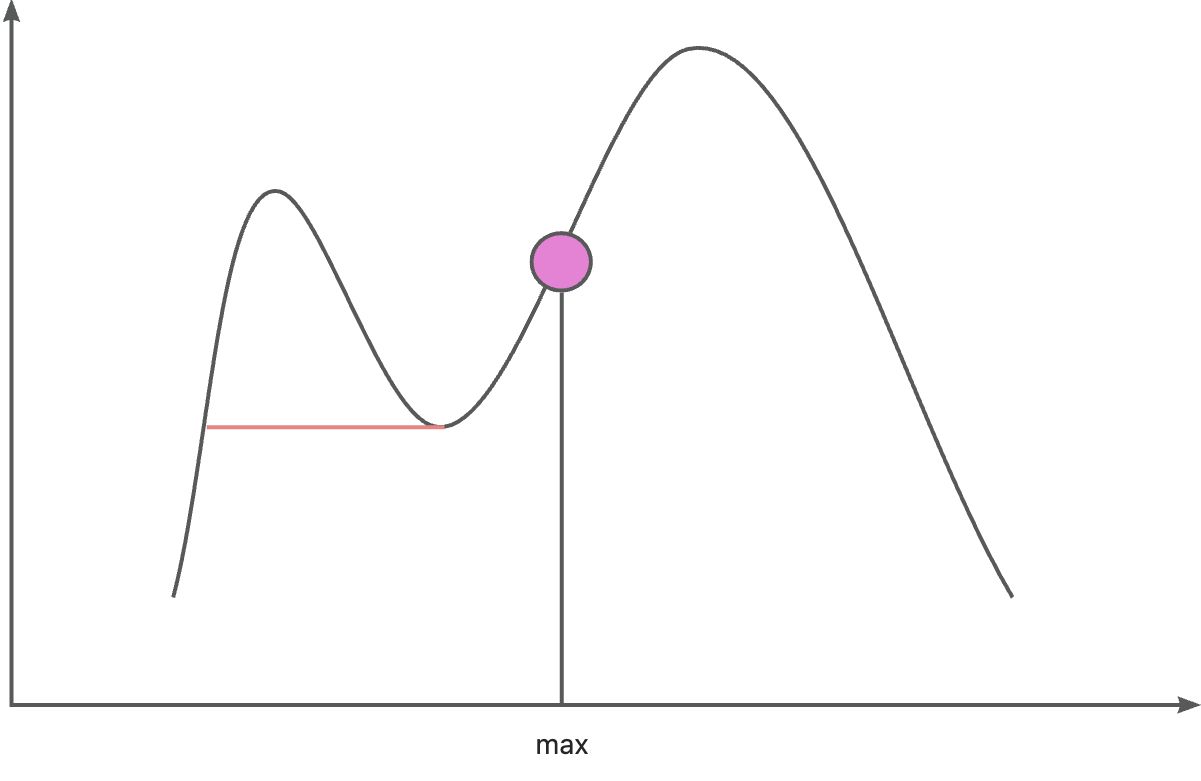

而最大值的取值我们有n种情况，我们最笨的办法就是将n种情况一一枚举出来，求他们的元素和，最后比较那个值当最大值时，元素和最大
但是很明显，这种方式的时间复杂度O(n2)，肯定会超时，所以我们接下来就要用魔法了：
假设我们能通过某种方式，将当前元素为最大值时，前方元素元素和求出来，将当前元素后方元素和求出来，最后一相加，就可以得到当前元素的元素和了。（为什么会有这种思想呢？因为很明显，最大值左/右侧的元素和计算是有联系的，然后我们就可以用动态规划啦）
我们如何求元素和呢？
我们先看左侧元素和，可以很容易发现

• 当maxHeights递增时，元素和 = 前一个元素和 + 当前元素值
• 当maxHeights递减时，元素和 = 当前元素值 * 下标

但是，如果前方并不是单纯的递增递减，如图所示，当前值是递减，但是他的元素和并不是我们刚才说的两种情况，我们还需要的得到x，来得到x前部分的元素和，即：x前元素和 + （max - x）* maxHeights[max]
这时，我们就要拿出我们今天的主角：单调栈
什么是单调栈呢？其实就是栈里的元素是递增或递减排列的的
那么我们这道题该如何应用？
我们这道题其实就是想直到x，那么如何知道呢？我们只要利用单调递增栈，将遍历到的元素一个一个放进去，然后将比当前元素大的出栈，小的留下，这样一来，栈的元素永远保持单调递增，而且当我们遇到上方的情况时，我们正好能将之前比当前值小的元素都留下来，这样一来，栈顶元素，就是我们想要的x，即上一个比当前值小的元素

题解：

class Solution {
    public long maximumSumOfHeights(List<Integer> maxHeights) {
        int n = maxHeights.size();
        long res = 0;
        long[] prefix = new long[n];
        long[] suffix = new long[n];
        Deque<Integer> stack1 = new ArrayDeque<Integer>();
        Deque<Integer> stack2 = new ArrayDeque<Integer>();

        for (int i = 0; i < n; i++) {
            // 将当前值设为栈里的最大值
            while (!stack1.isEmpty() && maxHeights.get(i) < maxHeights.get(stack1.peek())) {
                stack1.pop();
            }
            
            if (stack1.isEmpty()) {
                prefix[i] = (long) (i + 1) * maxHeights.get(i);
            } else {
                prefix[i] = prefix[stack1.peek()] + (long) (i - stack1.peek()) * maxHeights.get(i);
            }
            stack1.push(i);
        }

        for (int i = n - 1; i >= 0; i--) {
            while (!stack2.isEmpty() && maxHeights.get(i) < maxHeights.get(stack2.peek())) {
                stack2.pop();
            }
            if (stack2.isEmpty()) {
                suffix[i] = (long) (n - i) * maxHeights.get(i);
            } else {
                suffix[i] = suffix[stack2.peek()] + (long) (stack2.peek() - i) * maxHeights.get(i);
            }
            stack2.push(i);
            
            res = Math.max(res, prefix[i] + suffix[i] - maxHeights.get(i));
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

如果大家喜欢我的文章，希望可以给点个小小的赞，谢谢大家！我们下期再见！拜拜~~