2024年新算法||吸引-排斥优化算法(Attraction–Repulsion Algorithm)

本期介绍一种求解约束全局优化问题的元启发式搜索算法——吸引-排斥优化算法Attraction–Repulsion Optimization Algorithm,AROA。该算法模拟自然界中发生的吸引-排斥现象相关的平衡。该成果于2024年2月发表在中科院1区SCI期刊 Swarm and Evolutionary Computation（if = 10）。

一、亮点

1. 介绍了一种新颖的吸引-排斥搜索方案。
2. 提出的元启发式由平衡搜索运算符控制。
3. 算法在三个要求苛刻的CEC基准上得到验证。
   在这项研究中，提出了一种用于约束全局优化问题的新型元启发式搜索（MHS）算法。AROA引入了一种搜索策略，其中候选解决方案根据其邻域中解决方案的质量以及最佳候选方案在搜索空间中移动。候选方案由基于修正布朗运动、三角函数、随机选择的解决方案和记忆形式的局部搜索算子管理。

二、数学模型

2.1 种群初始化

所有种群的初始位置都是随机确定的
$X_i=x_{min}+rand\left(0,1\right)\cdot \left(x_{max}-x_{min}\right)$

2.2 吸引和排斥

选解决方案的位置根据总体其余部分获得的适应度信息更新。它对个体位置变化的贡献取决于种群成员之间的距离。
${\mathbf{a}}_{\mathrm{i}}=\frac{1}{n}{\sum }_{j=1}^{k}c\cdot \left({\mathbf{x}}_{\mathrm{j}}-{\mathbf{x}}_{\mathrm{i}}\right)\cdot I\left(d_{i,j},d_{i,max}\right)\cdot s\left(f_i,f_j\right),$

2.3 吸引最好的解

影响候选解决方案在搜索空间中位置的下一个因素是根据最佳解决方案的吸引力来确定的.在探索应起主导作用的优化过程开始时，假设最佳解应微弱地影响候选者，但随着迭代次数的增加，其影响更好地反映了算法开发阶段的意义，在AROA中，表示吸引引起的动作的向量计算为
b i = { c . m . ( x b e s t − x i ) r 1 ≥ p 1 c . m . ( a 1 ⊙ x b e s t − x i ) r 1 < p 1 \mathbf{b}_{\mathrm{i}}={\left\{

$$\begin{array}{l l}{c.m.\left(\mathbf{x_{best}}-\mathbf{x_{i}}\right)}&{r_{1}\geq p_{1}}\\ {c.m.\left(\mathbf{a_{1}}\odot\mathbf{x_{best}}-\mathbf{x_{i}}\right)}&{r_{1}\lt p_{1}}\end{array}$$ \right.} bi​={c.m.(xbest​−xi​)c.m.(a1​⊙xbest​−xi​)​r1​≥p1​r1​<p1​​

2.4 局部搜索算子

为了给算法配备一个开发策略，除了与最佳候选者的吸引力相关的策略之外，每个候选者还使用三个随机局部搜索算子中的一个。第一个算子受到布朗运动的启发，布朗运动通常用于模拟小粒子的步长[19]，[20]。它可以用正态分布来描述 ，然而，在所提出的方法中，均方差是通过添加当前迭代次数和搜索空间边界来修改的。
${\mathbf{r}}_{\mathbf{B}}={\mathbf{u}}_1\odot \mathcal{M}\left(0,f{r}_1\cdot \left(1-\frac{t}{t_{maz}}\right)\cdot \left({\mathbf{x}}_{\mathbf{max}}-{\mathbf{x}}_{\mathbf{min}}\right)\right)$

r t r i = { f r 2 ⋅ u 2 ⋅ ( 1 − t t m a x ) ⋅ sin ⁡ ( 2 r 5 π ) ⊙ ∣ a 2 ⊙ x w − x i ∣            r 4 < 0.5 f r 2 ⋅ u 2 ⋅ ( 1 − t t m a x ) ⋅ cos ⁡ ( 2 r 5 π ) ⊙ ∣ a 2 ⊙ x w − x i ∣                r 4 ≥ 0.5 \mathbf{r}_{\mathrm{tri}}={\left\{

$$\begin{array}{l l}{f r_{2}\cdot\mathbf{u}_{2}\cdot\left(1-{\frac{t}{t_{m a x}}}\right)\cdot\sin\left(2r_{5}\pi\right)\odot\left|\mathbf{a}_{2}\odot\mathbf{x}_{w}-\mathbf{x}_{\mathrm{i}}\right|\;\;\;\;\;r_{4}\lt 0.5}\\ {f r_{2}\cdot\mathbf{u}_{2}\cdot\left(1-{\frac{t}{t_{m a x}}}\right)\cdot\cos\left(2r_{5}\pi\right)\odot\left|\mathbf{a}_{2}\odot\mathbf{x}_{w}-\mathbf{x}_{\mathrm{i}}\right|\;\;\;\;\;\;\;r_{4}\geq0.5}\end{array}$$ \right.} rtri​=⎩ ⎨ ⎧​fr2​⋅u2​⋅(1−tmax​t​)⋅sin(2r5​π)⊙∣a2​⊙xw​−xi​∣r4​<0.5fr2​⋅u2​⋅(1−tmax​t​)⋅cos(2r5​π)⊙∣a2​⊙xw​−xi​∣r4​≥0.5​

基于种群的算子：影响所有解决方案

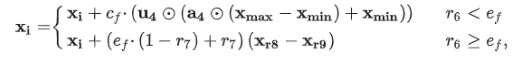
Karol Cymerys, Mariusz Oszust,Attraction–Repulsion Optimization Algorithm for Global Optimization Problems,Swarm and Evolutionary Computation,Volume 84, 2024, 101459, https://doi.org/10.1016/j.swevo.2023.101459.

3、完整代码下载

（1）AROA跑cec2017数据集（完整代码）
（2）AROA跑cec2005数据集（完整代码）