基于图嵌入的降维算法——边界流行嵌入Marginal Manifold Embedding（MME）

  0、前言      

        针对MFA 算法中样本点所选择的同类近邻点和异类近邻点之间没有必然的联系，和LDSA算法中样本点的近邻只有同类样本的问题，边界流行嵌入算法MME被提出。

1、MME算法原理

        MME与MFA与LDSA类似，都需要确定每个样本的同类近邻和异类近邻并分别构建本征图和惩罚图。他们的核心思想都是通过线性映射，让原有数据集中的不同类别容易区分。区别在于同类近邻和异类近邻如何构建，以及目标函数如何表达。

        MME同类边界邻域与异类边界邻域确定示意图如下：（图片来源于文献，感谢作者的精美绘图）

      图1  MME寻找边界点示意图

        图1解析：先确定样本点的异类边界邻域集合，并计算异类边界点的均值，然后寻找与异类边界均值最近的且标签与样本点系统的k个样本构成其同类边界邻域集合。由此可见，每个样本的同类近邻点和异类近邻点之间建立起必然的联系。

      图2为MME边界点分析图：（图片来源于文献，感谢作者的精美绘图）

图2 MME边界点分析图 

      图3是MFA边界点分析图：（图片来源于文献，感谢作者的精美绘图）

       

图3  MFA边界点分析图

         图4是 LSDA边界点分析图：（图片来源于文献，感谢作者的精美绘图）

 图4   LSDA边界点分析

        对比图2、3、4可以看出：MME算法中，每个样本点形成的同类边界子流形和异类边界子流形有着紧密的联系；离群点通常位于样本点的边界，MME算法在为每个样本点构造同类边界邻域和异类边界邻域的时候，很容易将离群点收入到边界邻域内，这在一定程度上能够减弱离群点给算法带来的负面影响。

2、 MME目标函数：

       类内权重矩阵构建：

        类间权重矩阵构建：

       类内重构误差：

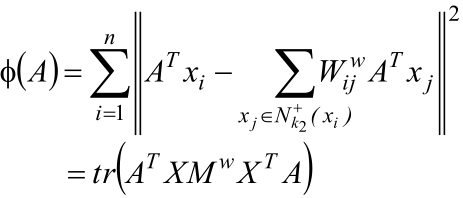
       其中： 

       类间重构误差：

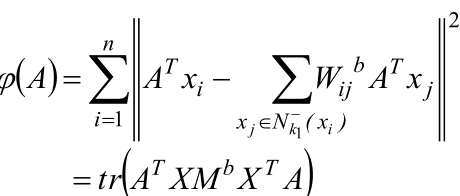
       其中： 

       MME目标函数：

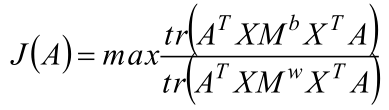
   3、改进点分析

       MME在分析MFA及LSDA等方法特点基础上，针对存在的一些典型问题，进行改进突破，主要贡献是 ①同类边界子流形和异类边界子流形有着紧密的联系；②减弱离群点给算法带来的负面影响。

       笔者认为在MME贡献基础上，还可以在以下方面进行改进：

     ①非线性化

     ②相似度量方式改进

     ③图1图2可以看出，样本的同类边界基本上都位于该类与其他类的分界处或者说在该类的边缘，意味着同类样本的同类边界点重合可能性很高，基于目标函数要求，最小化同类重构误差，意味着该类样本整体要向该类的边缘（同类边界点在边缘）靠近，其他类亦如此，这在类间重合度高的情况下不利于区分。所以可以将同类（非近邻）间的聚集性纳入考虑，并在目标函数中体现。

     ④与第③点类似，样本的异类边界点也基本上是该类与异类的交界处，即处于其他类面向该类的边缘处（同样重复度高）。异类重构误差仅仅考虑了与这有限个异类边界点的距离最大化，但是并不能代表与异类剩余大部分样本的距离最大化。所以可以将异类间的整体距离纳入考虑，并在目标函数中体现。

    说明:上述仅仅代表个人观点，没有十全十美的方法，也没有最好的方法，只有各种各样的解决问题的角度和思维，上述改进点仅仅适用于现有常规的图嵌入降维算法理论，并不代表最新观点。当然各个算法都有其独特的优势和使用场合，没有最好的，只有更适合的。

  4、MME效果分析