从前慢现在也慢

这个屌丝很懒，什么也没留下！

热门标签

【动态规划】简单多状态

作者：从前慢现在也慢 | 2024-05-12 06:10:50

踩

【动态规划】简单多状态

文章目录

动态规划（简单多状态）

动态规划（简单多状态）

1. 按摩师

题目链接

状态表示

dp[i]表示到i位置的时候预约的最大时长。但是这个题目我们可以选择接或不接。因此可以继续划分为两个子状态：
- f[i]表示：到i位置时接受的最大时长
- g[i]表示：到i位置时不接受的最大时长
状态转移方程
初始化

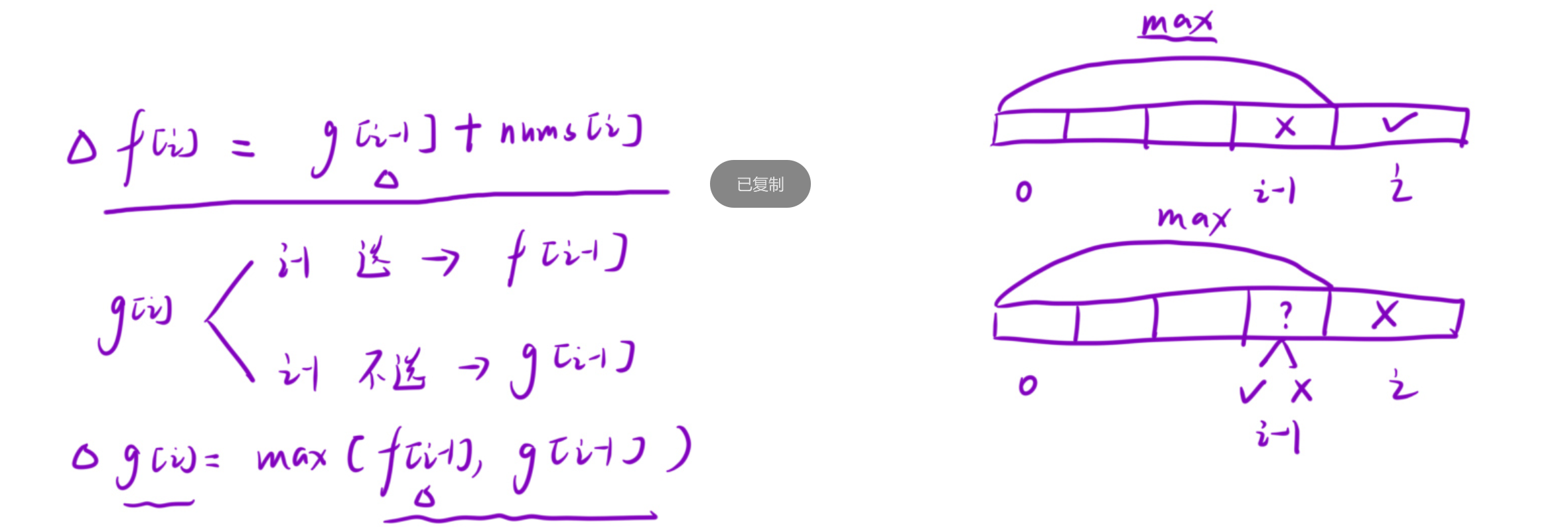
因为这个题目比较简单，所以不需要使用虚拟节点的方法，初始化是为了后面填表的时候不越界

f[0] = nums[0], g[0] = 0
填表

从左到右
返回值

接受最后一个或者不接受的最大值

AC代码：

class Solution 
{
public:
    int massage(vector<int>& nums) 
    {
        int n = nums.size();
        if (n == 0) return 0;
        vector<int> f(n);
        auto g = f;
        f[0] = nums[0], g[0] = 0;
        for (int i = 1; i < n; i++)
        {
            f[i] = g[i - 1] + nums[i];
            g[i] = max(f[i - 1], g[i - 1]);
        }
        return max(f[n - 1], g[n - 1]);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

2. 打家劫舍 ||

题目链接

分析：

由于房间是连续的，也就是一个环，因此可以分类讨论：

偷第一个时，第二个和最后一个不能偷
不偷第一个，可以偷第二个和最后一个

因此只需要两种情况的最大值就可以

状态表示

dp[i]表示偷到i时的最大金额，但是依然可以划分为两种情况偷或不偷

f[i]表示偷i时的最大金额

g[i]表示不偷i时的最大金额
状态转移方程
初始化

保证后续的填表不越界
填表

从左到右，两个一起填
返回值

最大值

AC代码：

class Solution 
{
public:
    int rob(vector<int>& nums) 
    {
        int x = 0, y = 0;
        int n = nums.size();
        x += nums[0];
        x += recursion(2, n - 2, nums);
        y += recursion(1, n - 1, nums);
        return max(x, y);
    }
    int recursion(int left, int right, vector<int> &v)
    {
        if (left > right) return 0;
        int n = v.size();
        vector<int> f(n);
        auto g = f;
        f[left] = v[left]; // 初始化
        for (int i = left + 1; i <= right; i++)
        {
            f[i] = g[i - 1] + v[i];
            g[i] = max(g[i - 1], f[i - 1]);
        }
        return max(f[right], g[right]);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

3. 删除并获得点数

题目链接

分析：我们把所有数字的点数之和，放到一个数组当中，在进行一次打家劫舍就可以了

把原数组转换成一个新数组，新数组的下标i所对应的值为原数组的元素i在原数组中数字的总和，比如原数组[2, 2, 3, 3, 3, 4],转换为新数组就是[0, 0, 4, 9, 4]。在新数组中，下标0和1表示在原数组中没有0和1这两个数，新数组下标2的值是4，表示在原数组中，所有2的总和是4。转换的目的就是可以从新数组中得到删除nums[i]而得到的点数，也就是可以打劫的金额。因为删除nums[i]后，还要删除nums[i] + 1和nums[i] - 1，在新数组中就意味着不能取相邻的元素，不能取相邻的元素和打家劫舍也是一样的。接下来就可以使用打家劫舍的方式解答了

AC代码：

class Solution 
{
public:
    const int N = 10001;
    int deleteAndEarn(vector<int>& nums) 
    {
        vector<int> arr(N);
        for (auto e : nums) arr[e] += e;
        vector<int> g(N);
        auto f = g;
        for (int i = 1; i < N; i++)
        {
            f[i] = g[i - 1] + arr[i];
            g[i] = max(g[i - 1], f[i - 1]);
        }
        return max(g[N - 1], f[N - 1]);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

4. 粉刷房子

题目链接

状态表示

dp[i]表示到i时，所需的最少费用。但是到i的时候可以有三种情况我们需要分三个子状态

dp[i][0], dp[i][1], dp[i][2]
状态转移方程
初始化

采用虚拟节点的方式
填表
返回值

返回三个表中的最小值

AC代码：

class Solution 
{
public:
    int minCost(vector<vector<int>>& costs) 
    {
        // 0: 红色 1：蓝色 2：绿色
        int n = costs.size();
        vector<vector<int>> dp(n + 1, vector<int>(3));
        for (int i = 1; i <= n; i++)
        {
            dp[i][0] = min(dp[i - 1][1], dp[i - 1][2]) + costs[i - 1][0];
            dp[i][1] = min(dp[i - 1][0], dp[i - 1][2]) + costs[i - 1][1];
            dp[i][2] = min(dp[i - 1][0], dp[i - 1][1]) + costs[i - 1][2];
        }
        int ret = INT_MAX;
        for (int i = 0; i < 3; i++)
        {
            ret = min(ret, dp[n][i]);
        }
        return ret;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

5. 最佳买卖股票时机含冷冻期

题目链接

状态表示

dp[i]表示到i位置时的最大利润，但是到达i位置的时候仍然有3种子状态
- dp[i][0]，表示i过后处于买入状态
- dp[i][1]，表示i过后处于可交易状态
- dp[i][2]，表示i过后处于冷冻期状态
状态转移方程

像这种状态之间可以相互转换的，我们可以采用如下方法分析：
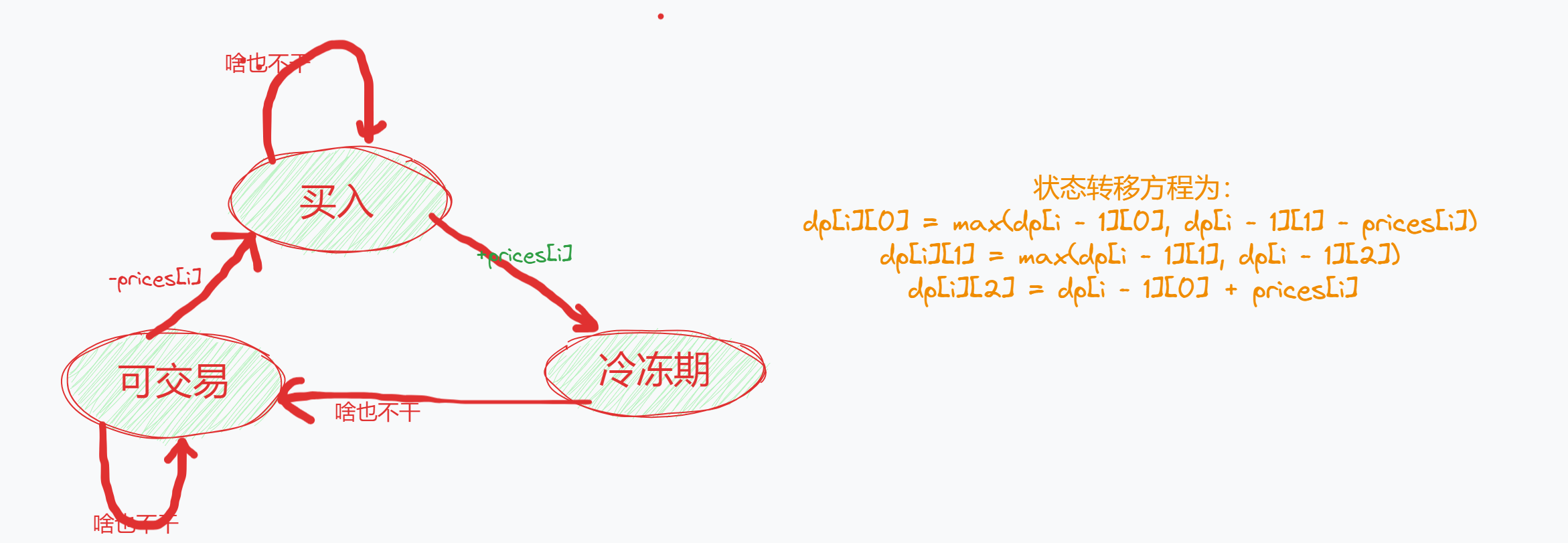
初始化

dp[0][0] = -prices[0], dp[0][1] = 0, dp[0][2] = 0
填表

三张表同时填
返回值

返回三中状态最后的最大值

AC代码：

class Solution 
{
public:
    int maxProfit(vector<int>& prices) 
    {
        int n = prices.size();
        vector<vector<int>> dp(n, vector<int>(3));
        dp[0][0] = -prices[0];
        for (int i = 1; i < n; i++)
        {
            dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][2]);
            dp[i][2] = dp[i - 1][0] + prices[i];
        }
        return max(max(dp[n - 1][0], dp[n - 1][1]), dp[n - 1][2]);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

6. 买卖股票的最佳时机含手续费

题目链接

状态表示

dp[i]表示到i位置的时候，最大的利润但是到i位置的时候是有两种状态的

dp[i][0]：表示是买入状态

dp[i][1]表示卖出状态
状态转移方程
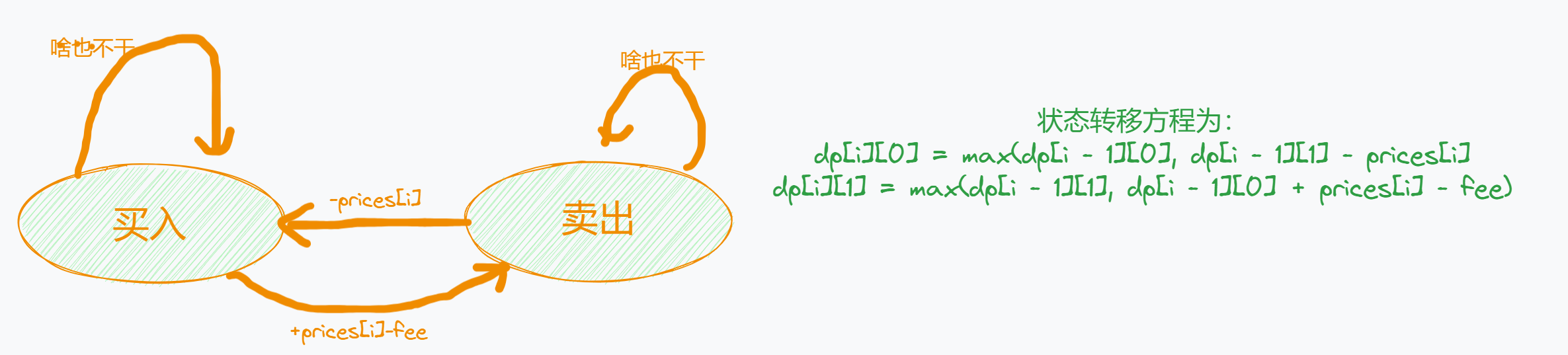
初始化

刚开始如果是买入状态dp[0][0] = -prices[0]
填表
返回值

AC代码：

class Solution 
{
public:
    int maxProfit(vector<int>& prices, int fee) 
    {
        int n = prices.size();
        vector<vector<int>> dp(n, vector<int>(2));
        dp[0][0] = -prices[0];
        for (int i = 1; i < n; i++)
        {
            dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i] - fee);
        }
        return max(dp[n - 1][0], dp[n - 1][1]);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

7. 买卖股票的最佳时机 |||

题目链接

状态表示

dp[i]表示到i位置的最大利润，但是还分为几个状态

f[i][j]表示到i是第j次买入的最大利润

g[i][j]表示到i是第j次买入的最大利润
状态转移方程
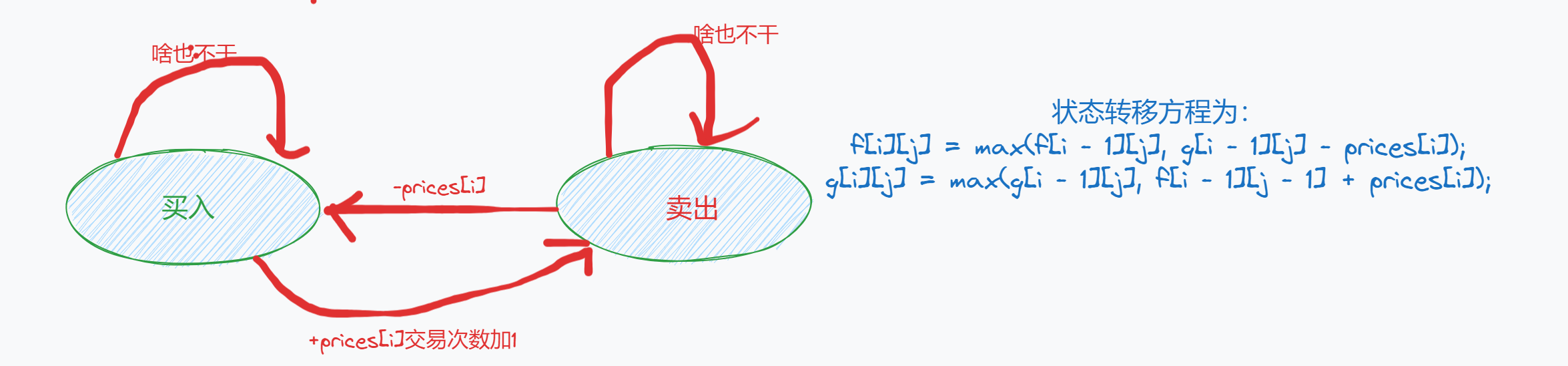
初始化

f[0][0] = -prices[0], g[0][0] = 0
填表

从上往下，每一行从左到右
返回值

卖出状态最后的几个中的最大值

AC代码：

class Solution 
{
public:
    const int N = 0x3f3f3f3f;
    int maxProfit(vector<int>& prices) 
    {
        int n = prices.size();
        vector<vector<int>> f(n, vector<int>(3, -N));
        auto g = f;
        f[0][0] = -prices[0], g[0][0] = 0;
        for (int i = 1; i < n; i++)
        {
            for (int j = 0; j < 3; j++)
            {
                f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i]);
                g[i][j] = g[i - 1][j];
                if (j - 1 >= 0) g[i][j] = max(g[i][j], f[i - 1][j - 1] + prices[i]);
            }
        }
        int ret = 0;
        for (int i = 0; i < 3; i++)
        {
            ret = max(ret, g[n - 1][i]);
        }
        return ret;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

8. 买卖股票的最佳时机 IV

题目链接

状态表示

还是分为两个子状态

f[i][j]表示到i位置买入状态第j次买股票的最大利润

g[i][j]表示到i位置卖出状态第j次买股票的最大利润
状态转移方程
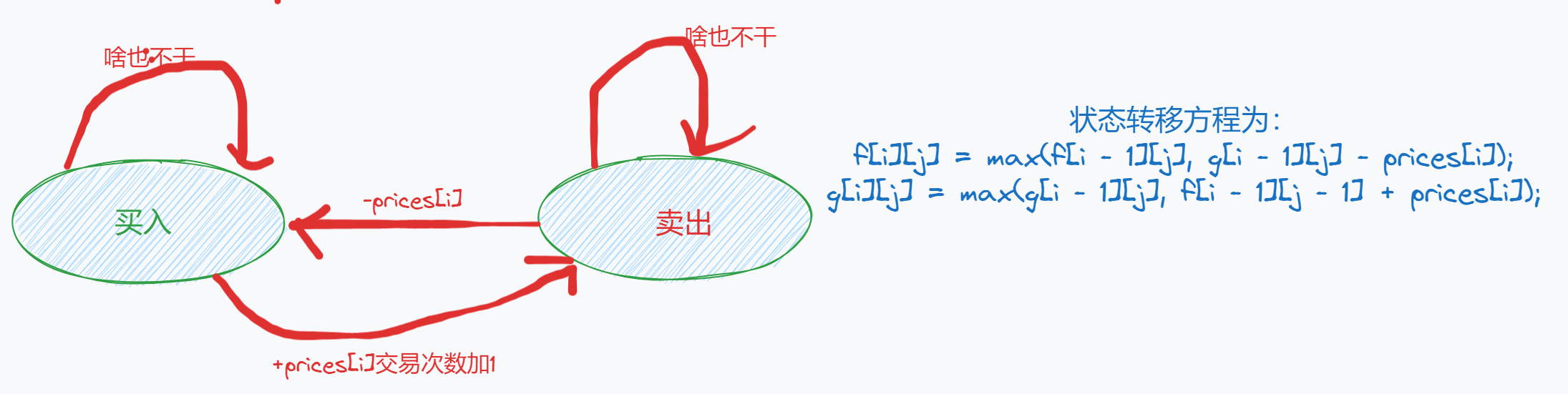
初始化

f[0][0] = -prices[0], g[0][0] = 0
填表

从上到下，从左到右
返回值

返回所有行的最大值

AC代码：

class Solution {
public:
    const int N = 0x3f3f3f3f;
    int maxProfit(int k, vector<int>& prices) {
        int n = prices.size();
        vector<vector<int>> f(n, vector<int>(k + 1, -N));
        auto g = f;
        f[0][0] = -prices[0], g[0][0] = 0;
        for (int i = 1; i < n; i++)
        {
            for (int j = 0; j <= k; j++)
            {
                f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i]);
                g[i][j] = g[i - 1][j];
                if (j - 1 >= 0) g[i][j] = max(g[i][j], f[i - 1][j - 1] + prices[i]);
            }
        }
        int ret = 0;
        for (int i = 0; i <= k; i++)
        {
            ret = max(ret, g[n - 1][i]);
        }
        return ret;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/从前慢现在也慢/article/detail/557902