matlab实现apriori算法源代码实验报告_apriori算法实验报告

一、实验目的

通过实验，加深数据挖掘中一个重要方法——关联分析的认识，其经典算法为apriori算法，了解影响apriori算法性能的因素，掌握基于apriori算法理论关联分析的原理和方法。

二、实验内容

对一数据集用apriori算法做关联分析，用matlab实现。

三、方法手段

关联规则挖掘的一个典型例子是购物篮分析。市场分析员要从大量的数据中发现顾客放入其购物篮中的不同商品之间的关系。如果顾客买牛奶，他也购买面包的可能性有多大？ 什么商品组或集合顾客多半会在一次购物时同时购买？例如，买牛奶的顾客有80%也同时买面包，或买铁锤的顾客中有70%的人同时也买铁钉，这就是从购物篮数据中提取的关联规则。分析结果可以帮助经理设计不同的商店布局。一种策略是：经常一块购买的商品可以放近一些，以便进一步刺激这些商品一起销售，例如，如果顾客购买计算机又倾向于同时购买财务软件，那么将硬件摆放离软件陈列近一点，可能有助于增加两者的销售。另一种策略是：将硬件和软件放在商店的两端，可能诱发购买这些商品的顾客一路挑选其他商品。
关联规则是描述数据库中数据项之间存在的潜在关系的规则,形式为 ,其中 , 是数据库中的数据项.数据项之间的关联规则即根据一个事务中某些项的出现,可推导出另一些项在同一事务中也出现。

四、Apriori算法

1.算法描述

Apriori算法的第一步是简单统计所有含一个元素的项集出现的频率,来决定最大的一维项目集。在第k步,分两个阶段,首先用一函数sc_candidate(候选),通过第(k-1)步中生成的最大项目集Lk-1来生成侯选项目集Ck。然后搜索数据库计算侯选项目集Ck的支持度. 为了更快速地计算Ck中项目的支持度, 文中使用函数count_support计算支持度。
Apriori算法描述如下：
(1) C1={candidate1-itemsets};
(2) L1={c∈C1|c.count≥minsupport};
(3) for(k=2,Lk-1≠Φ,k++)　　 //直到不能再生成最大项目集为止
(4) Ck=sc_candidate(Lk-1);　 //生成含k个元素的侯选项目集
(5) for all transactions t∈D //办理处理
(6) Ct=count_support(Ck,t);　 //包含在事务t中的侯选项目集
(7) for all candidates c∈Ct
(8) c.count=c.count+1;
(9) next
(10) Lk={c∈Ck|c.count≥minsupport};
(11) next
(12) resultset=resultset∪Lk
其中, D表示数据库；minsupport表示给定的最小支持度；resultset表示所有最大项目集。
Sc_candidate函数
该函数的参数为Lk-1,即: 所有最大k-1维项目集,结果返回含有k个项目的侯选项目集Ck。事实上,Ck是k维最大项目集的超集,通过函数count_support计算项目的支持度,然后生成Lk。
该函数是如何完成这些功能的, 详细说明如下:
首先, 通过对Lk-1自连接操作生成Ck,称join(连接)步,该步可表述为:
insert into Ck　
select P.item1,P.item2,…,P.itemk-1,Q.itemk-1 from Lk-1P,Lk-1Q　
where P.item1=Q.item1,…,P.itemk-2=Q.itemk-2,P.itemk-1<Q.itemk-1
若用集合表示:Ck={X∪X’|X,X’∈Lk-1,|X∩X’|=k-2}
然后,是prune(修剪)步,即对任意的c,c∈Ck, 删除Ck中所有那些(k-1)维子集不在Lk-1中的项目集,得到侯选项目集Ck。表述为：
for all itemset　c∈Ck　　
for all (k-1)维子集s of c　
if(s不属于Lk-1) then delete c from Ck;
用集合表示:Ck={X∈Ck|X的所有k-1维子集在Lk-1中}

2.Apriori算法的举例

示例说明Apriori算法运作过程，有一数据库D, 其中有四个事务记录, 分别表示为

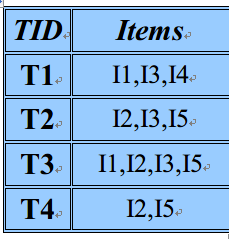
在Apriori算法中每一步创建该步的侯选集。统计每个侯选项目集的支持度,并和预定义的最小支持度比较,来确定该步的最大项目集。
首先统计出一维项目集,即C1.这里预定义最小支持度minsupport=2,侯选项目集中满足最小支持度要求的项目集组合成最大的1-itemsets。为生成最大的2-itemsets,使用了sc_candidate函数中join步,即：L1joinL1，并通过prune步删除那些C2的那些子集不在L1中的项目集。生成了侯选项目集C2。搜索D中4个事务,统计C2中每个侯选项目集的支持度。然后和最小支持度比较,生成L2。侯选项目集C3是由L2生成.要求自连接的两个最大2-itemsets中,第一个项目相同,在L2中满足该条件的有{I2,I3},{I2,I5}.这两个集合经过join步后, 产生集合{I2，I3，I5}.在prune步中,测试{I2，I3，I5}的子集{I3，I5},{I2，I3},{I2，I5}是否在L2中,由L2可以知道{I3,I5},{I2,I3},{I2,I5}本身就是最大2-itemsets.即{I2,I3,I5}的子集都是最大项目集.那么{I2,I3,I5}为侯选3-itemset.然后搜索数据库中所有事务记录,生成最大的3-tiemsets L3。此时, 从L3中不能再生成侯选4-itemset 。Apriori算法结束.

算法的图例说明

五、实验结果

test.txt格式及内容如下：

实验结果如下：

六、实验总结

Apriori算法可以很有效地找出数据集中存在的关联规则且能找出最大项的关联规则，但从以上的算法执行过程可以看到Apriori算法的缺点:
第一,在每一步产生侯选项目集时循环产生的组合过多，没有排除不应该参与组合的元素；第二,每次计算项集的支持度时，都对数据库D中的全部记录进行了一遍扫描比较，如果是一个大型的数据库的话，这种扫描比较会大大增加计算机系统的I/O开销。而这种代价是随着数据库的记录的增加呈现出几何级数的增加。因此人们开始寻求一种能减少这种系统1/O开销的更为快捷的算法。

七、实验程序

function my_apriori(X,minsup)  
clc;
%%%%主函数，输入X数据集，判断产生大于minsup最小支持度的关联规则
%%%%%%%%%%%%%%%%%%%%%%%%%%打开test.txt文件
file = textread('test.txt','%s','delimiter','\n','whitespace','');
[m,n]=size(file);
for i=1:m
    words=strread(file{i},'%s','delimiter',' ');
    words=words';
    X{i}=words;
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
minsup=0.3; %预先定义支持度

[m,N]=size(X); %求X的维数
temp=X{1}; %用已暂存变量存储所有不同项集
for i=2:N
   temp=union(temp,X{i}); %找出所有不同项（种类）
end    

%%%%%%%%%%%%%%%%%%%%找出k-频繁项
L=Sc_candidate(temp);    %找出2-项候选项集
sum=1;     %统计满足条件的最多项集
while(~isempty(L{1})) %循环终止条件为第k次频繁项集为空
    sum=sum+1;
    C=count_support(L,X,minsup);   %挑选出满足最小支持度的k-频繁项
    %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    sprintf('%s%d%s','满足要求的',sum,'次频繁项集依次为')  %显
    for i=1:size(C,1)                                    %示
        disp(C{i,1});                                   %部
    end                                               %分
    %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%    L=gen_rule(C);    %依次产生k-频繁项(依据apriori算法规则）
End


%%%%%%%%%%%%%%%%%%%%%%%%各个子程序如下
function y=cell_union(X,Y)   %实现两cell元组合并功能,由k-1项集增加到k项集函数
[m,n]=size(X);
if(~iscellstr(X)) %判断X是否元组
    L{1}=X;
    L{1,2}=Y;
else
    L=X;
    L{1,n+1}=Y;
end
y=L;

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function y=count_support(L,X,minsup)
%找出符合大于支持度sup的候选集,L为候选集，X为总数据集
X=X';%转置
%%%%%%%%%%%%%%%%%统计频繁项
[m,n]=size(L);
[M,N]=size(X);
count=zeros(m,1);
for i=1:m
    for j=1:M
        if(ismember(L{i},X{j}))
            count(i)=count(i)+1;
        end
    end
end

%%%%%%%%%%%删除数据表中不频繁的项
p=1;
C=cell(1);
for i=1:m
    if(count(i)>minsup*M)         %小于支持度的项为不频繁数，将删除,大于的保留
        C{p}=L{i};
        p=p+1;
    end
end
y=C';

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function y=gen_rule(C) %apriori算法规则判断是否产生k-候选项集
if(~isempty(C{1})) %判断C是否为空
    [M,N]=size(C);
    [m,n]=size(C{1});
    temp1=C;
    L=cell(1);
    for i=1:M
        temp2{i}=temp1{i}{n};
        temp1{i}{n}=[];
    end
    p=1;
    for i=1:M
        for j=i+1:M
            if(isequal(temp1{i},temp1{j}))   %判断前k-1项候选集是否相等
                L{p}=cell_union(C{i},temp2{j});  %若相等，则增加至k-项集
                p=p+1;
            end
        end
    end
    y=L';
else
    y=cell(1);%否则y返回空
end

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function y=Sc_candidate(C)   %产生2-项候选集函数
C=C'; %转置
[m,n]=size(C);
bcount=zeros(m*(m-1)/2,1);
L=cell(m*(m-1)/2,1);
p=1;
for i=1:m-1   %注意
    for j=i+1:m
        L{p}=cell_union(C{i},C{j}); %产生2-项候选集
        p=p+1;
    end
end
y=L;

function y=count_support(L,X,minsup)
%找出符合大于支持度sup的候选集,L为候选集，X为总数据集
X=X';%转置
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%统计频繁项
[m,n]=size(L);
[M,N]=size(X);
count=zeros(m,1);
for i=1:m
    for j=1:M
        if(ismember(L{i},X{j}))
            count(i)=count(i)+1;
        end
    end
end

%%%%%%%%%%%%%%%%%%%%%%%删除数据表中不频繁的项
p=1;
C=cell(1);
for i=1:m
    if(count(i)>minsup*M)         %小于支持度的项为不频繁数，将删除,大于的保留
        C{p}=L{i};
        p=p+1;
    end
end
y=C'; 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140