排序算法-C语言实现_不带“哨兵”的插入排序c语言源代码

一、分类

---

二、实现

1.直接插入排序

//无哨兵，0号单元存储实际值
void StraightInsertSort(int A[], int n)	//n是元素个数
{
	int i, j, tmp;
	for (i = 1; i < n; i++)	//依次将A[1]~A[n-1]插入到前面已排序序列
	{
		if (A[i - 1] > A[i])	//比较前驱元素和当前元素大小，判断是否需要插入
		{
			tmp = A[i];	//待插入的值放到tmp暂存
			for (j = i - 1; tmp < A[j]; --j)	//从后往前查找待插入位置
			{
				A[j + 1] = A[j];	//元素向右移动
			}
			A[j + 1] = tmp;	//复制到插入位置
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

---

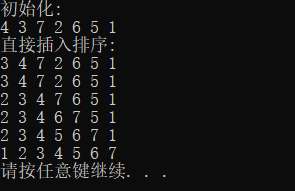
2.折半插入排序

//无哨兵，0号单元存储实际值
void BinaryInsertSort(int A[], int n)	//n是元素个数
{
	int i, j, low, high, mid, tmp;
	for (i = 1; i < n; i++)	//依次将A[1]~A[n-1]插入到前面已排序序列
	{
		tmp = A[i];	//待插入的值放到tmp暂存
		low = 0;
		high = i - 1;	//设置折半查找的范围
		while (low <= high)	//折半查找
		{
			mid = (low + high) / 2;	//取中间点(向左取整)
			if (A[mid] > tmp)
				high = mid - 1;	//查找左半子表
			else
				low = mid + 1;	//查找右半子表
		}
		for (j = i - 1; j >= high + 1; j--)	//high+1 为插入位置
		{
			A[j + 1] = A[j];
		}
		A[high + 1] = tmp;	//将值插入
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

---

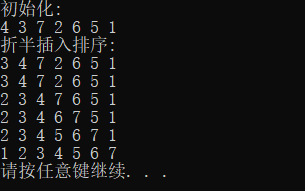
3.希尔排序

//无哨兵，0号单元存储实际值
void ShellSort(int A[], int n)	//n是元素个数
{
	int i, j, tmp, dk;
	for (dk = n / 2; dk >= 1; dk = dk / 2)	//位置增量值
	{
		for (i = dk; i < n; i++)	//依次将A[1]~A[n-1]插入到前面已排序序列
		{
			if (A[i - dk] > A[i])	//比较前驱元素和当前元素大小，判断是否需要插入
			{
				tmp = A[i];	//待插入的值放到tmp暂存
				for (j = i - dk; j >= 0 && tmp < A[j]; j -= dk)	//从后往前查找待插入位置
				{
					A[j + dk] = A[j];	//元素向右移动
				}
				A[j + dk] = tmp;	//复制到插入位置
			}
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

---

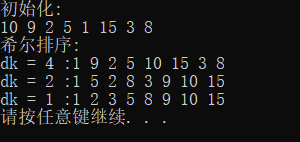
4.冒泡排序

void BubbleSort(int A[], int n)	//n是元素个数
{
	bool flag;
	int i, j, tmp;
	for (i = 0; i < n - 1; i++)	//循环n-1趟
	{
		flag = false;	//表示本趟冒泡是否发生交换的标志
		for (j = n - 1; j > i; j--)	//每趟循环的次数，从后向前找最小，升序排序
		{
			if (A[j - 1] > A[j])	//交换
			{
				tmp = A[j - 1];
				A[j - 1] = A[j];
				A[j] = tmp;
				flag = true;
			}
		}
		if (flag == false)	//本趟遍历没有发生交换说明已经有序
			return;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

---

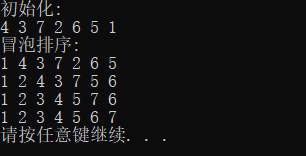
5.快速排序

int Partition(int A[], int low, int high)	//划分操作
{
	int pivot = A[low];	//将当前表中第一个元素设为枢轴值，对表进行划分
	while (low < high)
	{
		while (low < high && A[high] >= pivot)	
			high--;
		A[low] = A[high];	//将比枢轴值小的元素移动到左端
		while (low < high && A[low] <= pivot)	
			low++;
		A[high] = A[low];	//将比枢轴值大的元素移动到右端
	}
	A[low] = pivot;	//枢轴元素放到最终位置
	return low;		//返回最终位置
}

void QuickSort(int A[], int low, int high)
{
	int pivotpos;
	if (low < high)	//递归跳出条件
	{
		pivotpos = Partition(A, low, high);	//划分为两个子表
		QuickSort(A, low, pivotpos - 1);	//对子表递归排序	
		QuickSort(A, pivotpos + 1, high);
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

---

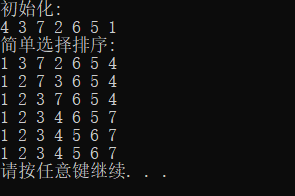
6.简单选择排序

void SelectSort(int A[], int n)	//n是元素个数
{
	int i, j, min, tmp;
	for (i = 0; i < n - 1; i++)	//循环n-1趟
	{
		min = i;				//min记录最小元素位置
		for (j = i + 1; j < n; j++)	//在A[i~n-1]中选择最小元素
			if (A[j] < A[min])
				min = j;		//更新最小元素位置
		if (min != j)			//交换
		{
			tmp = A[i];
			A[i] = A[min];
			A[min] = tmp;
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

---

7.堆排序

A[0]用于暂存，不存储实际数据

• 小根堆：L(i) <= L(2*i)且L(i) <= L(2*i+1)
• 大根堆：L(i) >= L(2*i)且L(i) >= L(2*i+1) (1<=i<=⌊n/2⌋)

void AdjustDown(int A[], int k, int len)	//将元素k向下进行调整
{
	int i;
	A[0] = A[k];	//A[0]用于暂存
	for (i = 2 * k; i <= len; i *= 2)	//沿k较大的子结点向下筛选
	{
		if (i < len && A[i] < A[i + 1])
			i++;			//取k较大的子结点的下标
		if (A[0] >= A[i])	//筛选结束
			break;
		else
		{
			A[k] = A[i];	//将A[i]调整到双亲结点上
			k = i;			//修改k值以便继续向下筛选
		}
	}
	A[k] = A[0];	//被筛选的节点的值放入最终位置
}

void BuildMaxHeap(int A[], int len)	//建立大根堆
{
	int i;
	for (i = len / 2; i > 0; i--)
	{
		AdjustDown(A, i, len);
	}
}

void HeapSort(int A[], int len)
{
	int i, tmp;
	BuildMaxHeap(A, len);		//初始建堆
	for (i = len; i > 1; i--)	//n-1趟的交换和建堆过程
	{
		tmp = A[i];				//交换
		A[i] = A[1];
		A[1] = tmp;
		AdjustDown(A, 1, i - 1);//把剩余的i-1个元素整理成堆
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

---

8.归并排序

int *B = (int *)malloc(n * sizeof(int));	//辅助数组B
void Merge(int A[], int low, int mid, int high)	//将前后相邻的两个有序表归并为一个有序表
{
	int i, j, k;
	for (k = low; k <= high; k++)
	{
		B[k] = A[k];	//将A中所有元素复制到B中
	}
	for (i = low, j = mid + 1, k = i; i <= mid && j <= high; k++)
	{
		if (B[i] <= B[j])	//比较B的左右两段中的元素
			A[k] = B[i++];	//将较小的值放到A中
		else
			A[k] = B[j++];
	}
	while (i <= mid)		//若第一个表未检测完
		A[k++] = B[i++];	//复制剩余元素到A中
	while (j <= high)		//若第二个表未检测完
		A[k++] = B[j++];	//复制剩余元素到A中
}

void MergeSort(int A[], int low, int high)
{
	int mid;
	if (low < high)
	{
		mid = (low + high) / 2;		//从中间划分两个子序列
		MergeSort(A, low, mid);		//对左侧子序列进行递归排序
		MergeSort(A, mid + 1, high);//对右侧子序列进行递归排序
		Merge(A, low, mid, high);	//归并
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

---

三、性能分析