LeetCode-160. 相交链表（C语言）

---

一、题目描述

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。

图示两个链表在节点 c1 开始相交：

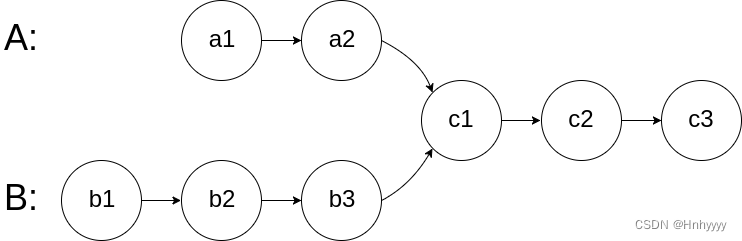
题目数据 保证 整个链式结构中不存在环。

注意，函数返回结果后，链表必须 保持其原始结构 。

自定义评测：

评测系统 的输入如下（你设计的程序 不适用 此输入）：

• intersectVal - 相交的起始节点的值。如果不存在相交节点，这一值为 0
• listA - 第一个链表
• listB - 第二个链表
• skipA - 在 listA 中（从头节点开始）跳到交叉节点的节点数
• skipB - 在 listB 中（从头节点开始）跳到交叉节点的节点数

评测系统将根据这些输入创建链式数据结构，并将两个头节点 headA 和 headB 传递给你的程序。如果程序能够正确返回相交节点，那么你的解决方案将被 视作正确答案 。

二、示例与提示

示例 1：

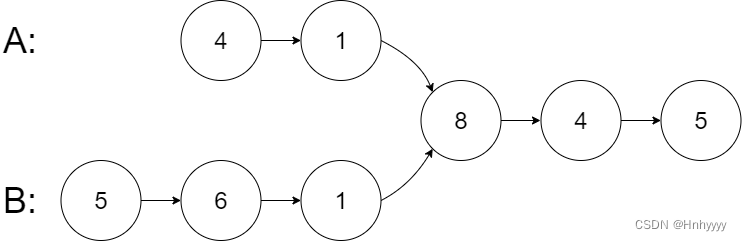
输入： intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
输出： Intersected at ‘8’
解释： 相交节点的值为 8 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,6,1,8,4,5]。
在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。
— 请注意相交节点的值不为 1，因为在链表 A 和链表 B 之中值为 1 的节点 (A 中第二个节点和 B 中第三个节点) 是不同的节点。换句话说，它们在内存中指向两个不同的位置，而链表 A 和链表 B 中值为 8 的节点 (A 中第三个节点，B 中第四个节点) 在内存中指向相同的位置。

示例 2：

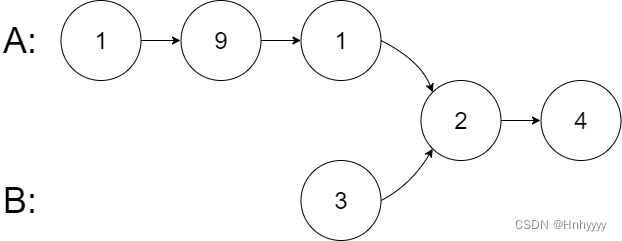
输入： intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出： Intersected at ‘2’
解释： 相交节点的值为 2 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [1,9,1,2,4]，链表 B 为 [3,2,4]。
在 A 中，相交节点前有 3 个节点；在 B 中，相交节点前有 1 个节点。

示例 3：

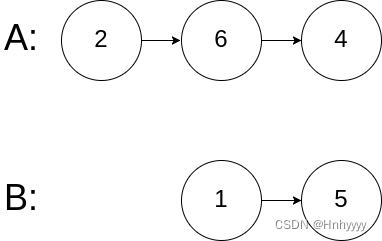
输入： intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出： null
解释： 从各自的表头开始算起，链表 A 为 [2,6,4]，链表 B 为 [1,5]。
由于这两个链表不相交，所以 intersectVal 必须为 0，而 skipA 和 skipB 可以是任意值。
这两个链表不相交，因此返回 null 。

提示

• listA 中节点数目为 m
• listB 中节点数目为 n
• 1 <= m, n <= 3 * 104
• 1 <= Node.val <= 105
• 0 <= skipA <= m
• 0 <= skipB <= n
• 如果 listA 和 listB 没有交点，intersectVal 为 0
• 如果 listA 和 listB 有交点，intersectVal == listA[skipA] == listB[skipB]

进阶： 你能否设计一个时间复杂度 O(m + n) 、仅用 O(1) 内存的解决方案？

三、思路

本题需要求两个单链表相交的起始节点，会很容易想到使用两个指针分别遍历两个链表，当指针相等时即为两链表相交节点。（注意： 交点 不是数值相等，而是 指针相等）

看如下两个链表，目前curA指向链表A的头结点，curB指向链表B的头结点：

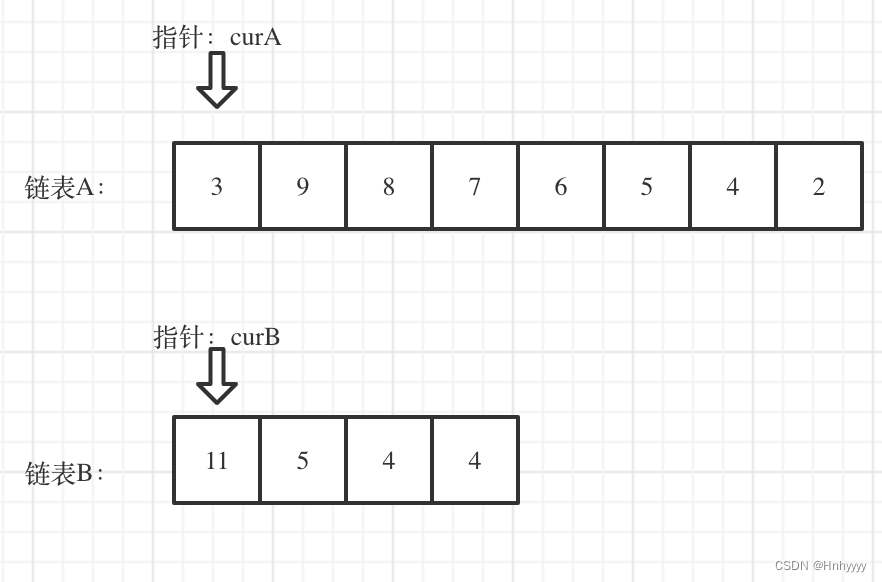
我们求出两个链表的长度，并求出两个链表长度的差值，然后让curA移动到，和curB末尾对齐的位置，如图：

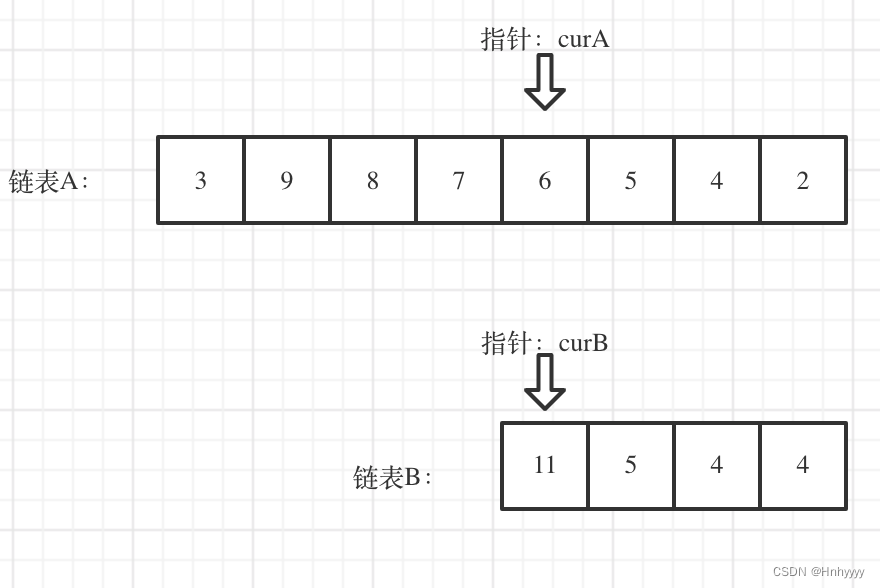
此时我们就可以比较curA和curB是否相同，如果不相同，同时向后移动curA和curB，如果遇到curA == curB，则找到交点。

否则循环退出，返回空指针。

四、代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {
    struct ListNode * curA = headA;
    struct ListNode * curB = headB;
    int lenA = 0, lenB = 0;
    // 求链表A的长度
    while(curA != NULL) {
      lenA++;
      curA = curA->next;
    }
    // 求链表B的长度
    while(curB != NULL) {
      lenB++;
      curB = curB->next;
    }
    // 注意此处要让 curA 与 curB 归位至表头
    curA = headA;
    curB = headB;
    // 让 curA 为最长链表的头，lenA为其长度
    if (lenA < lenB) {
      curA = headB;
      curB = headA;
      int t = lenA;
      lenA = lenB;
      lenB = t;
    }
    // 求长度差
    int gap = lenA - lenB;
    // 让 curA 和 curB 在同一起点上（末尾位置对齐）
    for (int i = 0; i < gap; i++) {
      curA = curA->next;
    }
    // 遍历 curA 和 curB，遇到相同则直接返回，否则同时向后移动
    while (curA != NULL) {
      if (curA == curB)
      return curA;
      curA = curA->next;
      curB = curB->next;
    }
    // 若未找到节点则返回NULL
    return NULL;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

复杂度分析

时间复杂度：O(n + m)