好不容易找到三元环的板子题……
三元环是什么
似乎三元环在有向图和无向图中都有定义,
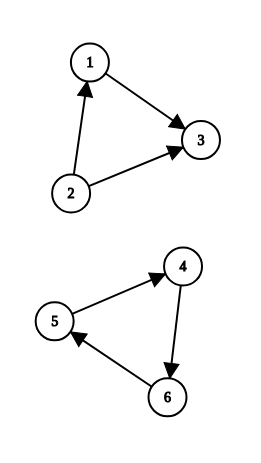
这里只介绍最基础求三元环的算法,和一些比较好的三元环题目模型。
求三元环算法
大多数求三元环的题对于边是否有向并没有要求,所以即便是有向图也可以建成无向边考虑求三元环。
通常来说统计的三元环都是要求有序的$(i,j,k)$三元组,所以我们对于图中的无向边,按照编号大向编号小方向建边。
暴力统计
暴力统计就是对于点$x$,枚举所有直接相连的点i,j然后判断i,j之间是否直接相连。
数据结构优化
显然我们可以用hash或者set/map来判断$u,v$间是否直接连边。
进一步优化
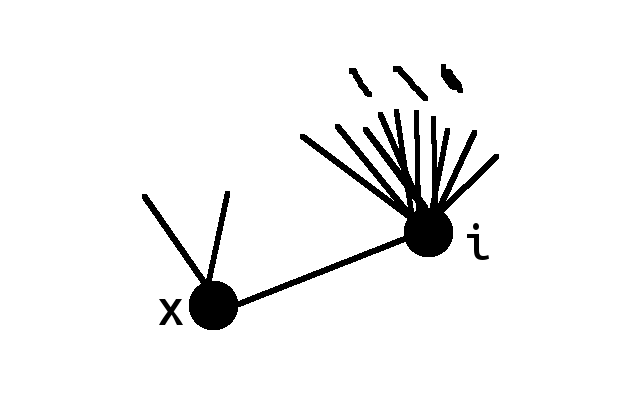
当遇到特殊情况时,我们做了很多不必要的比较。
考虑如下一个基本事实:在我们建出的图中,没有超过$\sqrt m$个点有超过$\sqrt m$的出度。
这个很显然,因为我们把边转成单向之后总数仍然是$m$。
然后,即便是最差情况下有$x$个点,$m$条边的完全图,也有$m=\frac{x(x-1)}{2}$,$x=\sqrt{2m}$。
于是自然想到记录每个点的出度,当从$x$枚举到的点$i$的度数大于$\sqrt m$时就从$x$一侧枚举点$j$,继而判断$i$和$j$之间是否有边相连;反之,则枚举$i$的出边,判断其和$x$是否有边相连。
这就是我用的三元环算法的流程,主要代码如下:
1 for (int i=3; i<=n; i++) 2 for (int j=head[i]; j!=-1; j=nxt[j]) 3 { 4 int x = edges[j]; 5 if (deg[x] > size) 6 for (int t=nxt[j]; t!=-1; t=nxt[t]) 7 { 8 int y = edges[t]; 9 if (y >= x) continue; 10 if (s[x].find(y)!=s[x].end()) 11 ans += ...; 12 } 13 else 14 for (int t=head[x]; t!=-1; t=nxt[t]) 15 { 16 int y = edges[t]; 17 if (s[i].find(y)!=s[i].end()) 18 ans += ...; 19 } 20 }
更大的改进?
似乎在建图时不盲目只用编号,而是结合度数会有更好的效果?待以研究吧。
几道例题
【三元环板子】bzoj3498: PA2009 Cakes
Description
N个点m条边,每个点有一个点权a。
对于任意一个三元环(j,j,k)(i<j<k),它的贡献
为max(ai,aj,ak)
求所有三元环的贡献和。
N<100000,,m<250000。
Input
The first line of the standard input contains two integers n and m (1<=N<=100000,1<=M<=250000) separated by a single space and denoting the number of confectioners at the convention and the number of pairs of them that like each other. The participants of the convention are numbered from 1 to N, The second line contains n integers pi (1<=Pi<=1000000) separated by single spaces and denoting the requirements of respective confectioners for flour (in decagrams). The following m lines contain data about pairs of contestants that like each other. Each of these lines contains two integers ai and bi (1<=ai,bi<=n Ai<>Bi) separated by a single space. They denote that confectioners ai and bi like each other. We assume that all pairs of participants of the convention apart from the ones listed in the input would not like to bake cakes together. Each pair of confectioners appears at most once in the input.
Output
The first and only line of the standard output should contain a single integer - the quantity of flour that will be used by all teams in total, in decagrams.
题目分析
就是板子题
1 #include<bits/stdc++.h> 2 const int maxn = 100035; 3 const int maxm = 250035; 4 5 struct Edge 6 { 7 int u,v; 8 }edgesSv[maxm]; 9 int head[maxn],nxt[maxm],edges[maxm],edgeTot; 10 int n,m,size,a[maxn],deg[maxn]; 11 std::set<int> s[maxn]; 12 long long ans; 13 14 void addedge(int u, int v) 15 { 16 edges[++edgeTot] = v, nxt[edgeTot] = head[u], head[u] = edgeTot; 17 } 18 int read() 19 { 20 char ch = getchar(); 21 int num = 0; 22 bool fl = 0; 23 for (; !isdigit(ch); ch = getchar()) 24 if (ch=='-') fl = 1; 25 for (; isdigit(ch); ch = getchar()) 26 num = (num<<1)+(num<<3)+ch-48; 27 if (fl) num = -num; 28 return num; 29 } 30 inline int max(int a, int b, int c){return std::max(std::max(a, b), c);} 31 bool cmp(Edge a, Edge b){return a.u==b.u?a.v<b.v:a.u<b.u;} 32 int main() 33 { 34 memset(head, -1, sizeof head); 35 n = read(), m = read(), size = (int)sqrt(m); 36 for (int i=1; i<=n; i++) a[i] = read(); 37 for (int i=1; i<=m; i++) 38 { 39 int &u = edgesSv[i].u, &v = edgesSv[i].v; 40 u = read(), v = read(); 41 if (u < v) std::swap(u, v); 42 deg[u]++; 43 } 44 std::sort(edgesSv+1, edgesSv+m+1, cmp); 45 for (int i=1; i<=m; i++) 46 { 47 addedge(edgesSv[i].u, edgesSv[i].v); 48 s[edgesSv[i].u].insert(edgesSv[i].v); 49 } 50 for (int i=3; i<=n; i++) 51 for (int j=head[i]; j!=-1; j=nxt[j]) 52 { 53 int x = edges[j]; 54 if (deg[x] > size) 55 for (int t=nxt[j]; t!=-1; t=nxt[t]) 56 { 57 int y = edges[t]; 58 if (y >= x) continue; 59 if (s[x].find(y)!=s[x].end()) 60 ans += max(a[i], a[x], a[y])*1ll; 61 } 62 else 63 for (int t=head[x]; t!=-1; t=nxt[t]) 64 { 65 int y = edges[t]; 66 if (s[i].find(y)!=s[i].end()) 67 ans += max(a[i], a[x], a[y])*1ll; 68 } 69 } 70 printf("%lld\n",ans); 71 return 0; 72 }
【巧妙模型】HDU4324Triangle LOVE
Problem Description
Now, scientists want to know whether or not there is a “Triangle Love” among N people. “Triangle Love” means that among any three people (A,B and C) , A loves B, B loves C and C loves A.
Your problem is writing a program to read the relationship among N people firstly, and return whether or not there is a “Triangle Love”.
Input
For each case, the first line contains one integer N (0 < N <= 2000).
In the next N lines contain the adjacency matrix A of the relationship (without spaces). Ai,j = 1 means i-th people loves j-th people, otherwise Ai,j = 0.
It is guaranteed that the given relationship is a tournament, that is, Ai,i= 0, Ai,j ≠ Aj,i(1<=i, j<=n,i≠j).
Output
Take the sample output for more details.
Sample Input
Sample Output
题目大意
判断竞赛图中是否存在三元环
题目分析
求三元环看上去很麻烦?又是要tarjan缩点,又是要判环长度?
不过竞赛图有一个非常妙的性质:若存在任意长度的环则必定存在三元环。这一点不是很容易独立想到,但是非常容易独立理解。
那么补集转化:竞赛图要怎么样才是没有环呢?
显然这个DAG的所有点的入度是0...n-1的排列。
那么就非常巧妙了。
1 #include<bits/stdc++.h> 2 const int maxn = 3005; 3 4 int deg[maxn],vis[maxn]; 5 int tt,n,scenario; 6 char ch[maxn]; 7 8 int main() 9 { 10 scanf("%d",&tt); 11 while (tt--) 12 { 13 scanf("%d",&n); 14 for (int i=1; i<=n; i++) 15 { 16 scanf("%s",ch); 17 for (int j=0; j<n; j++) 18 if (ch[j]=='1') deg[i]++; 19 } 20 ++scenario; 21 bool fl = 0; 22 for (int i=1; i<=n; i++) 23 if (vis[deg[i]]!=scenario) 24 vis[deg[i]] = scenario; 25 else{ 26 fl = 1;break; 27 } 28 memset(deg, 0, sizeof deg); 29 printf("Case #%d: %s\n",scenario,fl?"Yes":"No"); 30 } 31 return 0; 32 }
HDU6184Counting Stars
Problem Description
So he is counting stars now!
There are n stars in the sky, and little A has connected them by m non-directional edges.
It is guranteed that no edges connect one star with itself, and every two edges connect different pairs of stars.
Now little A wants to know that how many different "A-Structure"s are there in the sky, can you help him?
An "A-structure" can be seen as a non-directional subgraph G, with a set of four nodes V and a set of five edges E.
If
Input
For each test case, there are 2 positive integers n and m in the first line.
Output
题目大意
求共用一条边的三元环个数
题目分析
这个应该是正确的……但是被HDU的32mb卡死了
留坑
1 #include<bits/stdc++.h> 2 typedef long long ll; 3 const int maxn = 100005; 4 const int maxm = 200005; 5 6 struct Edge 7 { 8 int x,y; 9 }e[maxm]; 10 int edges[maxm],nxt[maxm],head[maxn],edgeTot; 11 int n,m,size,deg[maxn]; 12 std::set<int> f[maxn]; 13 std::map<std::pair<int, int>, int> s; 14 ll ans,cnt[maxm]; 15 16 int read() 17 { 18 char ch = getchar(); 19 int num = 0; 20 bool fl = 0; 21 for (; !isdigit(ch); ch = getchar()) 22 if (ch=='-') fl = 1; 23 for (; isdigit(ch); ch = getchar()) 24 num = (num<<1)+(num<<3)+ch-48; 25 if (fl) num = -num; 26 return num; 27 } 28 bool cmp(Edge a, Edge b){return a.x==b.x?a.y<b.y:a.x<b.x;} 29 void addedge(int u, int v) 30 { 31 edges[++edgeTot] = v, nxt[edgeTot] = head[u], head[u] = edgeTot; 32 } 33 void clears(std::set<int> &f) 34 { 35 std::set<int> emt; 36 std::swap(emt, f); 37 } 38 int main() 39 { 40 while (scanf("%d%d",&n,&m)!=EOF) 41 { 42 memset(head, -1, sizeof head); 43 memset(cnt, 0, sizeof cnt); 44 memset(deg, 0, sizeof deg); 45 size = (int)sqrt(m), ans = 0, edgeTot = 0; 46 s.clear(); 47 for (int i=1; i<=n; i++) clears(f[i]); 48 for (int i=1; i<=m; i++) 49 { 50 int &u = e[i].x, &v = e[i].y; 51 u = read(), v = read(); 52 if (u < v) std::swap(u, v); 53 deg[u]++; 54 } 55 std::sort(e+1, e+m+1, cmp); 56 for (int i=1; i<=m; i++) 57 { 58 int u = e[i].x, v = e[i].y; 59 addedge(u, v); 60 f[u].insert(v); 61 s[std::make_pair(u, v)] = edgeTot; 62 } 63 for (int i=3; i<=n; i++) 64 for (int j=head[i]; j!=-1; j=nxt[j]) 65 { 66 int x = edges[j]; 67 if (deg[x] > size) 68 for (int t=nxt[j]; t!=-1; t=nxt[t]) 69 { 70 int y = edges[t]; 71 if (y >= x) continue; 72 if (f[x].find(y)!=f[x].end()) 73 cnt[j]++, cnt[t]++, cnt[s[std::make_pair(x, y)]]++; 74 } 75 else 76 for (int t=head[x]; t!=-1; t=nxt[t]) 77 { 78 int y = edges[t]; 79 if (f[i].find(y)!=f[i].end()) 80 cnt[j]++, cnt[t]++, cnt[s[std::make_pair(i, y)]]++; 81 } 82 } 83 for (int i=1; i<=m; i++) 84 ans += cnt[i]*(cnt[i]-1)/2; 85 printf("%lld\n",ans); 86 } 87 return 0; 88 }
END


