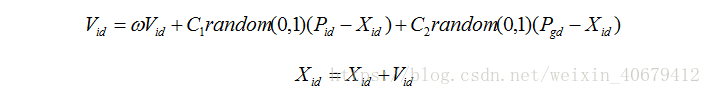【路径规划】基于粒子群算法求解VRPTW模型_vrptw数学模型

1 粒子群算法

1.1 研究背景

粒子群算法的发展过程。粒子群优化算法（Partical Swarm Optimization PSO），粒子群中的每一个粒子都代表一个问题的可能解，通过粒子个体的简单行为，群体内的信息交互实现问题求解的智能性。由于PSO操作简单、收敛速度快，因此在函数优化、 图像处理、大地测量等众多领域都得到了广泛的应用。 随着应用范围的扩大，PSO算法存在早熟收敛、维数灾难、易于陷入局部极值等问题需要解决，主要有以下几种发展方向。

（1）调整PSO的参数来平衡算法的全局探测和局部开采能力。如Shi和Eberhart对PSO算法的速度项引入了惯性权重，并依据迭代进程及粒子飞行情况对惯性权重进行线性（或非线性）的动态调整，以平衡搜索的全局性和收敛速度。2009年张玮等在对标准粒子群算法位置期望及方差进行稳定性分析的基础上，研究了加速因子对位置期望及方差的影响，得出了一组较好的加速因子取值。

（2）设计不同类型的拓扑结构，改变粒子学习模式，从而提高种群的多样性，Kennedy等人研究了不同的拓扑结构对SPSO性能的影响。针对SPSO存在易早熟收敛，寻优精度不高的缺点，于2003年提出了一种更为明晰的粒子群算法的形式：骨干粒子群算法（Bare Bones PSO，BBPSO）。

（3）将PSO和其他优化算法（或策略）相结合，形成混合PSO算法。如曾毅等将模式搜索算法嵌入到PSO算法中，实现了模式搜索算法的局部搜索能力与PSO算法的全局寻优能力的优势互补。

（4）采用小生境技术。小生境是模拟生态平衡的一种仿生技术，适用于多峰函数和多目标函数的优化问题。例如，在PSO算法中，通过构造小生境拓扑，将种群分成若干个子种群，动态地形成相对独立的搜索空间，实现对多个极值区域的同步搜索，从而可以避免算法在求解多峰函数优化问题时出现早熟收敛现象。 Parsopoulos提出一种基于“分而治之”思想的多种群PSO算法，其核心思想是将高维的目标函数分解成多个低维函数，然后每个低维的子函数由一个子粒子群进行优化，该算法对高维问题的求解提供了一个较好的思路。

不同的发展方向代表不同的应用领域，有的需要不断进行全局探测，有的需要提高寻优精度，有的需要全局搜索和局部搜索相互之间的平衡，还有的需要对高维问题进行求解。这些方向没有谁好谁坏的可比性，只有针对不同领域的不同问题求解时选择最合适的方法的区别。

1.2 相关模型和思想

粒子群算法（ Particle Swarm Optimization, PSO）最早是由Eberhart和Kennedy于1995年提出，它的基本概念源于对鸟群觅食行为的研究。设想这样一个场景：一群鸟在随机搜寻食物，在这个区域里只有一块食物，所有的鸟都不知道食物在哪里，但是它们知道当前的位置离食物还有多远。最简单有效的策略？寻找鸟群中离食物最近的个体来进行搜素。PSO算法就从这种生物种群行为特性中得到启发并用于求解优化问题。

用一种粒子来模拟上述的鸟类个体，每个粒子可视为N维搜索空间中的一个搜索个体，粒子的当前位置即为对应优化问题的一个候选解，粒子的飞行过程即为该个体的搜索过程．粒子的飞行速度可根据粒子历史最优位置和种群历史最优位置进行动态调整．粒子仅具有两个属性：速度和位置，速度代表移动的快慢，位置代表移动的方向。每个粒子单独搜寻的最优解叫做个体极值，粒子群中最优的个体极值作为当前全局最优解。不断迭代，更新速度和位置。最终得到满足终止条件的最优解。

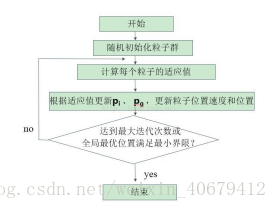
算法流程如下：

1、初始化

首先，我们设置最大迭代次数，目标函数的自变量个数，粒子的最大速度，位置信息为整个搜索空间，我们在速度区间和搜索空间上随机初始化速度和位置，设置粒子群规模为M，每个粒子随机初始化一个飞翔速度。

2、 个体极值与全局最优解

定义适应度函数，个体极值为每个粒子找到的最优解，从这些最优解找到一个全局值，叫做本次全局最优解。与历史全局最优比较，进行更新。

3、 更新速度和位置的公式

4、 终止条件

（1）达到设定迭代次数；（2）代数之间的差值满足最小界限

以上就是最基本的一个标准PSO算法流程。和其它群智能算法一样，PSO算法在优化过程中，种群的多样性和算法的收敛速度之间始终存在着矛盾．对标准PSO算法的改进，无论是参数的选取、小生境技术的采用或是其他技术与PSO的融合，其目的都是希望在加强算法局部搜索能力的同时，保持种群的多样性，防止算法在快速收敛的同时出现早熟收敛。

2 VRP模型

2.1车辆路径规划问题介绍

车辆路径规划问题，经过60年来的研究与发展，研究的目标对象，限制条件等均有所变化，已经从最初的简单车辆安排调度问题转变为复杂的系统问题。最初的车辆路径规划问题可以描述为：有一个起点和若干个客户点,已知各点的地理位置和需求,在满足各种约束的条件下,如何规划最优的路径,使其能服务到每个客户点,最后返回起点。通过施加不同的约束条件，改变优化的目标，可以衍生出不同种类的车辆路径规划问题。同时车辆路径规划问题属于典型的NP-hard问题，其精确算法能求解的规模很小，故启发式算法也就成了研究热点。

(2)VRPTW简介

VRPTW(Vehicle routing problem with time windows)即带时间窗的车辆路径规划问题，其对于每一需求点加入了时间窗的约束，即对于每一个需求点，设定服务开始的最早时间和最晚时间，要求车辆在时间窗内开始服务顾客。

需求点的时窗限制可以分为两种，一种是硬时间窗(Hard Time Window)，即要求车辆必须在时间窗内开始服务顾客，早到必须等待，迟到就拒收，另一种是软时间窗(Soft Time Window)，不一定要在时间窗内开始服务顾客，但是在时间窗外开始服务必须要惩罚，以惩罚代替等待与拒收是软时间窗和硬时时间窗的最大的区别。

VRPTW的数学模型如下：

（2.2）保证了每个顾客只被访问1次

（2.3）保证了装载的货物不超过容量

（2.4）（2.5）（2.6）确保了每辆车从depot出发最后回到depot

（2.7）（2.8）确保在时间窗内开始服务

3 代码

%
 
tic
clear
clc
%% 用importdata这个函数来读取文件
r101=importdata('r101.txt');
cap=200;                                                        %车辆最大装载量
%% 提取数据信息
E=r101(1,5);                                                    %配送中心时间窗开始时间
L=r101(1,6);                                                    %配送中心时间窗结束时间
vertexs=r101(:,2:3);                                            %所有点的坐标x和y
customer=vertexs(2:end,:);                                      %顾客坐标
cusnum=size(customer,1);                                       	%顾客数
v_num=25;                                                      	%车辆最多使用数目
demands=r101(2:end,4);                                          %需求量
a=r101(2:end,5);                                                %顾客时间窗开始时间[a[i],b[i]]
b=r101(2:end,6);                                                %顾客时间窗结束时间[a[i],b[i]]
s=r101(2:end,7);                                                %客户点的服务时间
h=pdist(vertexs);
dist=squareform(h);                                             %距离矩阵
%% 粒子群算法参数
alpha=10;                                                       %违反的容量约束的惩罚函数系数
belta=100;                                                      %违反时间窗约束的惩罚函数系数
NIND=50;                                                        %粒子数目
MAXGEN=100;                                                     %迭代次数
w=1;                                                            %惯性因子
wdamp=0.99;                                                     %惯性因子衰减率
c1=1.5;                                                         %个体学习因子
c2=2.0;                                                         %全局学习因子
XvMin=1;                                                        %Xv下限
XvMax=v_num;                                                    %Xv上限
XrMin=1;                                                        %Xr下限
XrMax=cusnum;                                                   %Xr上限
VvMin=-(v_num-1);                                            	%Vv下限
VvMax=v_num-1;                                                  %Vv上限
VrMin=-(cusnum-1);                                            	%Vr下限
VrMax=cusnum-1;                                                 %Vr上限
%% 初始化粒子群位置
init_vc=init(cusnum,a,demands,cap);                             %构造初始解
population=initpopCW(init_vc,NIND,cusnum,XvMin,XvMax,XrMin,XrMax,VvMin,VvMax,VrMin,VrMax);
ObjV=calObj(population,v_num,cap,demands,a,b,L,s,dist,alpha,belta); %计算各个粒子的目标函数值
gbest_pos=population{1,1}(1:2,:);                               %假设第一个粒子位置为全局最优位置
gbest_obj=ObjV(1,1);                                            %第一个粒子位置的目标函数值
pbest_pos=cell(NIND,1);                                         %初始化各个粒子的个体最优位置
pbest_obj=ObjV;                                                 %初始化各个粒子的个体最优的目标函数值
for i=1:NIND
    particle=population{i,1};                                   %第i个粒子
    position=particle(1:2,:);                                   %第i个粒子的位置
    pbest_pos{i,1}=position;                                    %初始化这个粒子的个体最优
    if pbest_obj(i,1)<gbest_obj
        %更新初始种群中的全局最优粒子
        gbest_obj=pbest_obj(i,1);
        gbest_pos=position;
    end
end
globalVC=decode(gbest_pos,v_num);                               %初始全局最优配送方案
%统计一个配送方案的总成本、车辆使用数目、行驶总距离、违反约束路径数目、违反约束顾客数目
[cost,NV,TD,vio_NV,vio_cus]=statistic(globalVC,a,b,s,L,dist,demands,cap,alpha,belta);
disp(['初始全局最优解总成本为：',num2str(cost),'，车辆使用数目为：',num2str(NV),...
    '，行驶总距离为：',num2str(TD),'，违反约束路径数目为：',num2str(vio_NV),'，违反约束顾客数目为：',num2str(vio_cus)]);
BestCost=zeros(MAXGEN,1);                                       %记录每次迭代的全局最优目标函数值
%% 主循环
gen=1;                                                          %计数器
while gen<=MAXGEN
    %% 更新各个粒子的位置和速度
    for i=1:NIND
        particle=population{i,1};                               %第i个粒子
        position=particle(1:2,:);                              	%第i个粒子的位置
        Xv=position(1,:);
        Xr=position(2,:);
        velocity=particle(3:4,:);                               %第i个粒子的速度
        Vv=velocity(1,:);
        Vr=velocity(2,:);
        %% 更新速度
        velocity=w*velocity+ +c1*rand([2,cusnum]).*(pbest_pos{i,1}-position)...
            +c2*rand([2,cusnum]).*(gbest_pos-position);
        %% 速度越界处理
        velocity(1,:)=max(velocity(1,:),VvMin);
        velocity(1,:)=min(velocity(1,:),VvMax);
        velocity(2,:)=max(velocity(2,:),VrMin);
        velocity(2,:)=min(velocity(2,:),VrMax);
        %% 更新位置
        position=position+velocity;
        position(1,:)=ceil(position(1,:));          %对Xv向上取整
        %% 速度镜像影响
        IsOutside=(position(1,:)<XvMin | position(1,:)>XvMax | position(2,:)<XrMin | position(2,:)>XrMax);
        velocity(IsOutside)=-velocity(IsOutside);
        %% 位置越界处理
        position(1,:)=max(position(1,:),XvMin);
        position(1,:)=min(position(1,:),XvMax);
        position(2,:)=max(position(2,:),XrMin);
        position(2,:)=min(position(2,:),XrMax);
        %% 对第i个粒子解码出的配送方案进行relocate操作
        VC=decode(position,v_num);
        RVC=relocate(VC,cap,demands,a,b,L,s,dist,alpha,belta);
        position=change(RVC,cusnum);
        %% 计算第i个粒子目标函数值
        cost=costFuction(RVC,a,b,s,L,dist,demands,cap,alpha,belta);
        %% 更新个体最优
        if cost<pbest_obj(i,1)
            pbest_pos{i,1}=position;
            pbest_obj(i,1)=cost;
            %%  更新全局最优
            if pbest_obj(i,1)<gbest_obj
                gbest_pos=pbest_pos{i,1};
                gbest_obj=pbest_obj(i,1);
            end
        end
        %% 更新第i个粒子的速度和位置
        particle=[position;velocity];
        population{i,1}=particle;
    end
    %% 记录各代全局最优解，打印各代全局最优解
    BestCost(gen)=gbest_obj;
    globalVC=decode(gbest_pos,v_num);                               %初始全局最优配送方案
    %统计一个配送方案的总成本、车辆使用数目、行驶总距离、违反约束路径数目、违反约束顾客数目
    [cost,NV,TD,vio_NV,vio_cus]=statistic(globalVC,a,b,s,L,dist,demands,cap,alpha,belta);
    disp(['第',num2str(gen),'代全局最优解总成本为：',num2str(cost),'，车辆使用数目为：',num2str(NV),...
        '，行驶总距离为：',num2str(TD),'，违反约束路径数目为：',num2str(vio_NV),'，违反约束顾客数目为：',num2str(vio_cus)]);
    w=w*wdamp;
    %% 更新计数器
    gen=gen+1;
end
%% 将全局最优粒子解码为全局最优配送方案
globalVC=decode(gbest_pos,v_num);
%% 对全局最优配送方案进行局部搜索
globalVC=relocate_gbest(globalVC,cap,demands,a,b,L,s,dist,alpha,belta);
%% 统计全局最优配送方案的总成本、车辆使用数目、行驶总距离、违反约束路径数目、违反约束顾客数目
    [cost,NV,TD,vio_NV,vio_cus]=statistic(globalVC,a,b,s,L,dist,demands,cap,alpha,belta);
    disp(['最终全局最优解总成本为：',num2str(cost),'，车辆使用数目为：',num2str(NV),...
        '，行驶总距离为：',num2str(TD),'，违反约束路径数目为：',num2str(vio_NV),'，违反约束顾客数目为：',num2str(vio_cus)]);
%% 画出全局最优配送方案路线图
draw_Best(globalVC,vertexs);
%% Results
figure;
%plot(BestCost,'LineWidth',2);
semilogy(BestCost,'LineWidth',2);
xlabel('迭代次数');
ylabel('全局最优目标函数值');
grid on;
toc