从前慢现在也慢

这个屌丝很懒，什么也没留下！

热门标签

Leetcode数据结构入门_lico数据结构

作者：从前慢现在也慢 | 2024-07-05 01:39:31

踩

lico数据结构

在预习数据结构，所以写了力扣的数据入门题单，做个整理。

Leetcode数据结构入门

第一天——第五天：数组

第六天：字符串

第七天——第八天：链表

第九天：队列/栈

第十天——第十四天：树

第一天

（1）217.存在重复元素

给定一个整数数组，判断是否存在重复元素。

如果存在一值在数组中出现至少两次，函数返回 true 。如果数组中每个元素都不相同，则返回 false 。

示例 1:
输入: [1,2,3,1]
输出: true
1
2
示例 2:
输入: [1,2,3,4]
输出: false
1
2
示例 3:
输入: [1,1,1,3,3,4,3,2,4,2]
输出: true
1
2

我的思路：

创建一个map的哈希表，遍历数组，只要大于1就输出true，遍历完都未输出true就输出false。

代码：

class Solution {
public:
    bool containsDuplicate(vector<int>& nums) {
        map<int,int> list;
        for(int num:nums)
        {
            list[num]++;
            if(list[num]>1)return true;
        }
        return false;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12

官方题解思路：

1.排序后查找

古早C代码：

int compar(const void *p1, const void *p2)
{
    int a,b;
    a=*(int*)p1;b=*(int*)p2;
    return a-b;
}
bool containsDuplicate(int* nums, int numsSize){
qsort(nums,numsSize,sizeof(int),compar);
int i;
for(i=0;i<numsSize-1;i++){
    if(nums[i]==nums[i+1])return true;
}
return false;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

官方C++：

class Solution {
public:
    bool containsDuplicate(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        int n = nums.size();
        for (int i = 0; i < n - 1; i++) {
            if (nums[i] == nums[i + 1]) {
                return true;
            }
        }
        return false;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13

2.哈希表

class Solution {
public:
    bool containsDuplicate(vector<int>& nums) {
        unordered_set<int> s;
        for (int x: nums) {
            if (s.find(x) != s.end()) {
                return true;
            }
            s.insert(x);
        }
        return false;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13

（2）53.最大子序和

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

示例 2：

输入：nums = [1]
输出：1

示例 3：

输入：nums = [0]
输出：0

示例 4：

输入：nums = [-1]
输出：-1

示例 5：

输入：nums = [-100000]
输出：-100000

提示：

1 <= nums.length <= 3 * 104
-105 <= nums[i] <= 105

进阶：如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的分治法求解。

我的思路：
前缀和，不断求最大值，注意本身最大和只有一个元素的情况。

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        if(nums.size()==1)return nums[0];
        //前缀和
        vector<int> add;
        int sum = 0;
        for(int num:nums)
        {
            sum+=num;
            add.push_back(sum);
        }
        int max = INT_MIN;
        for(int i=0;i<nums.size();i++)
        {
            for(int j=i+1;j<nums.size();j++)
            {
                if(add[j]-add[i]>max)
                {
                    max = add[j]-add[i];
                }
                if(add[i]>max)
                {
                    max = add[i];
                }
            }
        }
        if(add[nums.size()-1]>max)max = add[nums.size()-1];
        return max;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

官方题解：

1.动态规划

请添加图片描述

//关键是这个方程只取最大，和加和的构想

class Solution {
public:    
	int maxSubArray(vector<int>& nums) {        
	int pre = 0, maxAns = nums[0];        
	for (const auto &x: nums) {            
		pre = max(pre + x, x);            
		maxAns = max(maxAns, pre);        
		}        
	return maxAns;    
	}
};
1
2
3
4
5
6
7
8
9
10
11

2.分治（线段树）

请添加图片描述

class Solution {
public:
    struct Status {
        int lSum, rSum, mSum, iSum;
    };

    Status pushUp(Status l, Status r) {
        int iSum = l.iSum + r.iSum;
        int lSum = max(l.lSum, l.iSum + r.lSum);
        int rSum = max(r.rSum, r.iSum + l.rSum);
        int mSum = max(max(l.mSum, r.mSum), l.rSum + r.lSum);
        return (Status) {lSum, rSum, mSum, iSum};
    };

    Status get(vector<int> &a, int l, int r) {
        if (l == r) {
            return (Status) {a[l], a[l], a[l], a[l]};
        }
        int m = (l + r) >> 1;
        Status lSub = get(a, l, m);
        Status rSub = get(a, m + 1, r);
        return pushUp(lSub, rSub);
    }

    int maxSubArray(vector<int>& nums) {
        return get(nums, 0, nums.size() - 1).mSum;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

线段树

相关阅读：线段树详解（原理，实现与应用）_岩之痕-CSDN博客_线段树

第二天

（1）1.两数之和

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出和为目标值 target 的那两个整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。

你可以按任意顺序返回答案。

示例 1：

输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。
示例 2：

输入：nums = [3,2,4], target = 6
输出：[1,2]
示例 3：

输入：nums = [3,3], target = 6
输出：[0,1]

提示：

2 <= nums.length <= 104
-109 <= nums[i] <= 109
-109 <= target <= 109
只会存在一个有效答案
进阶：你可以想出一个时间复杂度小于 O(n2) 的算法吗？

思路：直接遍历呗【躺】

class Solution {
public:    
vector<int> twoSum(vector<int>& nums, int target) {        
//前缀和        
	vector<int> ans;        
	for(int i=0;i<nums.size();i++)        
	{            
		for(int j=i+1;j<nums.size();j++)            
		{                
		if(nums[i]+nums[j]==target)                
		{                    
		ans.push_back(i);                    
		ans.push_back(j);                    
		return ans;                
		}            
	}        
	}        
	return ans;    
	}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

官方题解：

1.暴力枚举

思路相同，但是返回直接用的{}：

class Solution {
public:    
vector<int> twoSum(vector<int>& nums, int target) {        
	int n = nums.size();       
 	for (int i = 0; i < n; ++i) {            
 	for (int j = i + 1; j < n; ++j) {                
 		if (nums[i] + nums[j] == target) {                    
 			return {i, j};                
 			}            
 		}        
 	}        
 return {};    
 }
 };
1
2
3
4
5
6
7
8
9
10
11
12
13
14

2.哈希表

请添加图片描述

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int, int> hashtable;
        for (int i = 0; i < nums.size(); ++i) {
            auto it = hashtable.find(target - nums[i]);
            if (it != hashtable.end()) {
                return {it->second, i};
            }
            hashtable[nums[i]] = i;
        }
        return {};
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14

找数->找不到就存自己->找到了就返回

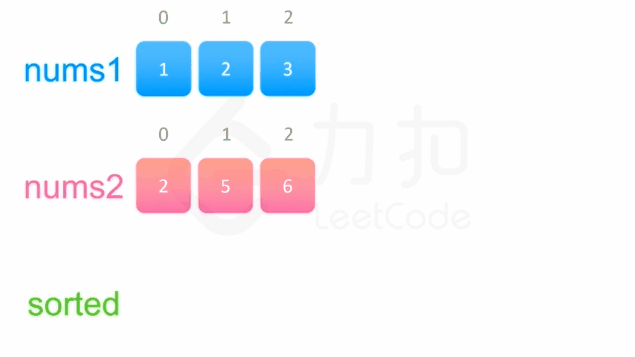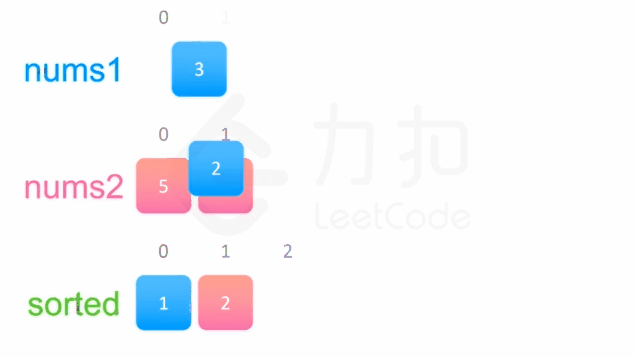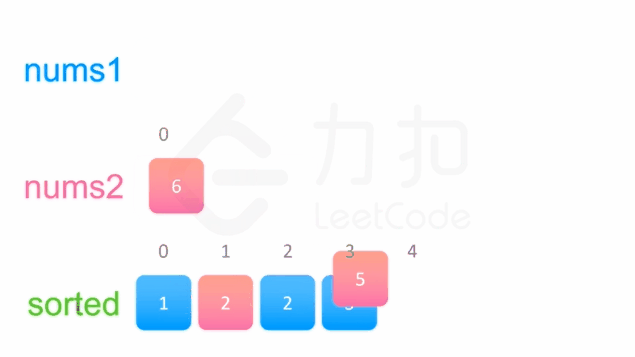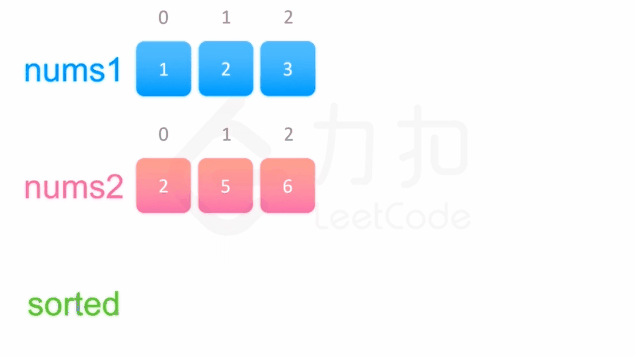
（2）88.合并两个有序数组

给你两个按非递减顺序排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。

请你合并 nums2 到 nums1 中，使合并后的数组同样按非递减顺序排列。

注意：最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n 。

示例 1：

输入：nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出：[1,2,2,3,5,6]
解释：需要合并 [1,2,3] 和 [2,5,6] 。
合并结果是 [1,2,2,3,5,6] ，其中斜体加粗标注的为 nums1 中的元素。
示例 2：

输入：nums1 = [1], m = 1, nums2 = [], n = 0
输出：[1]
解释：需要合并 [1] 和 [] 。
合并结果是 [1] 。
示例 3：

输入：nums1 = [0], m = 0, nums2 = [1], n = 1
输出：[1]
解释：需要合并的数组是 [] 和 [1] 。
合并结果是 [1] 。
注意，因为 m = 0 ，所以 nums1 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中。

提示：

nums1.length == m + n
nums2.length == n
0 <= m, n <= 200
1 <= m + n <= 200
-109 <= nums1[i], nums2[j] <= 109

进阶：你可以设计实现一个时间复杂度为 O(m + n) 的算法解决此问题吗？

思路：先把num2加到nums1里，再按递增（非递减）排序。

class Solution {
public:
    void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
        //非递减==递增==sort
        for(int num:nums2)nums1[m++]=num;
        sort(nums1.begin(),nums1.end());
    }
};
1
2
3
4
5
6
7
8

官方题解：

1.合并后排序

思路相同

2.双指针

方法一没有利用数组nums 1与 nums 2 已经被排序的性质。为了利用这一性质，我们可以使用双指针方法。这一方法将两个数组看作队列，每次从两个数组头部取出比较小的数字放到结果中。如下面的动画所示：

gif1

我们为两个数组分别设置一个指针 p1 与 p2 来作为队列的头部指针。代码实现如下：

class Solution {
public:
    void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
        int p1 = 0, p2 = 0;
        int sorted[m + n];
        int cur;
        while (p1 < m || p2 < n) {
            if (p1 == m) {
                cur = nums2[p2++];
            } else if (p2 == n) {
                cur = nums1[p1++];
            } else if (nums1[p1] < nums2[p2]) {
                cur = nums1[p1++];
            } else {
                cur = nums2[p2++];
            }
            sorted[p1 + p2 - 1] = cur;
        }
        for (int i = 0; i != m + n; ++i) {
            nums1[i] = sorted[i];
        }
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

//取小==递增

3.逆向双指针

class Solution {
public:
    void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
        int p1 = m - 1, p2 = n - 1;
        int tail = m + n - 1;
        int cur;
        while (p1 >= 0 || p2 >= 0) {
            if (p1 == -1) {
                cur = nums2[p2--];
            } else if (p2 == -1) {
                cur = nums1[p1--];
            } else if (nums1[p1] > nums2[p2]) {
                cur = nums1[p1--];
            } else {
                cur = nums2[p2--];
            }
            nums1[tail--] = cur;
        }
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

//取大放后==递增，这个逆向真的妙

第三天

（1）350.两个数组的交集II

给定两个数组，编写一个函数来计算它们的交集。

示例 1：

输入：nums1 = [1,2,2,1], nums2 = [2,2]
输出：[2,2]
示例 2:

输入：nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出：[4,9]

说明：

输出结果中每个元素出现的次数，应与元素在两个数组中出现次数的最小值一致。
我们可以不考虑输出结果的顺序。
进阶：

如果给定的数组已经排好序呢？你将如何优化你的算法？
如果 nums1 的大小比 nums2 小很多，哪种方法更优？
如果 nums2 的元素存储在磁盘上，内存是有限的，并且你不能一次加载所有的元素到内存中，你该怎么办？

思路：找长度小的数组，然后遍历找长度长的是否有相同元素，找到后删除并加入ans。

代码：

class Solution {
public:
    vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {
        vector<int> ans;
        int m=nums1.size(),n=nums2.size();
        if(m>n)
        {
            for(int num:nums2)
            {
                auto it = find(nums1.begin(),nums1.end(),num);
                if(it!=nums1.end())
                {
                    ans.push_back(num);
                    nums1.erase(it);
                }
            }
        }
        else
        {
            for(int num:nums1)
            {
                auto it = find(nums2.begin(),nums2.end(),num);
                if(it!=nums2.end())
                {
                    ans.push_back(num);
                    nums2.erase(it);
                }
            }
        }
        return ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

官方题解：

1.哈希表

由于同一个数字在两个数组中都可能出现多次，因此需要用哈希表存储每个数字出现的次数。对于一个数字，其在交集中出现的次数等于该数字在两个数组中出现次数的最小值。（属实是没想到）

首先遍历第一个数组，并在哈希表中记录第一个数组中的每个数字以及对应出现的次数，然后遍历第二个数组，对于第二个数组中的每个数字，如果在哈希表中存在这个数字，则将该数字添加到答案，并减少哈希表中该数字出现的次数。

为了降低空间复杂度，首先遍历较短的数组并在哈希表中记录每个数字以及对应出现的次数，然后遍历较长的数组得到交集。

class Solution {
public:
    vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {
        if (nums1.size() > nums2.size()) {
            return intersect(nums2, nums1);
        }
        unordered_map <int, int> m;
        for (int num : nums1) {
            ++m[num];
        }
        vector<int> intersection;
        for (int num : nums2) {
            if (m.count(num)) {
                intersection.push_back(num);
                --m[num];
                if (m[num] == 0) {
                    m.erase(num);
                }
            }
        }
        return intersection;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

2.排序+双指针

如果两个数组是有序的，则可以使用双指针的方法得到两个数组的交集。

首先对两个数组进行排序，然后使用两个指针遍历两个数组。

初始时，两个指针分别指向两个数组的头部。每次比较两个指针指向的两个数组中的数字，如果两个数字不相等，则将指向较小数字的指针右移一位，如果两个数字相等，将该数字添加到答案，并将两个指针都右移一位。当至少有一个指针超出数组范围时，遍历结束。

class Solution {
public:
    vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {
        sort(nums1.begin(), nums1.end());
        sort(nums2.begin(), nums2.end());
        int length1 = nums1.size(), length2 = nums2.size();
        vector<int> intersection;
        int index1 = 0, index2 = 0;
        while (index1 < length1 && index2 < length2) {
            if (nums1[index1] < nums2[index2]) {
                index1++;
            } else if (nums1[index1] > nums2[index2]) {
                index2++;
            } else {
                intersection.push_back(nums1[index1]);
                index1++;
                index2++;
            }
        }
        return intersection;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

如果nums 2的元素存储在磁盘上，磁盘内存是有限的，并且你不能一次加载所有的元素到内存中。那么就无法高效地对nums2进行排序，因此推荐使用方法一而不是方法二。在方法一中,nums2只关系到查询操作，因此每次读取 nums2 中的一部分数据，并进行处理即可。

（2）121.买卖股票的最佳时机

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择某一天买入这只股票，并选择在未来的某一个不同的日子卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

示例 1：

输入：[7,1,5,3,6,4]
输出：5
解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。
示例 2：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 没有交易完成, 所以最大利润为 0。

思路：暴力过不了

官方题解：

1.暴力

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n = (int)prices.size(), ans = 0;
        for (int i = 0; i < n; ++i){
            for (int j = i + 1; j < n; ++j) {
                ans = max(ans, prices[j] - prices[i]);
            }
        }
        return ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12

2. 一次遍历（类似双指针）

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n = (int)prices.size(), ans = 0,low = prices[0];
        for(int price:prices)
        {
            if(price<low)low = price;
            if(price-low>ans)ans = price-low;
        }
        return ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12

第四天

（1）566.重塑矩阵

在 MATLAB 中，有一个非常有用的函数 reshape ，它可以将一个 m x n 矩阵重塑为另一个大小不同（r x c）的新矩阵，但保留其原始数据。

给你一个由二维数组 mat 表示的 m x n 矩阵，以及两个正整数 r 和 c ，分别表示想要的重构的矩阵的行数和列数。

重构后的矩阵需要将原始矩阵的所有元素以相同的行遍历顺序填充。

如果具有给定参数的 reshape 操作是可行且合理的，则输出新的重塑矩阵；否则，输出原始矩阵。

示例 1：

输入：mat = [[1,2],[3,4]], r = 1, c = 4
输出：[[1,2,3,4]]
示例 2：

输入：mat = [[1,2],[3,4]], r = 2, c = 4
输出：[[1,2],[3,4]]

首先判断是否合理，合理就行遍历并存储。

class Solution {
public:
    vector<vector<int>> matrixReshape(vector<vector<int>>& mat, int r, int c) {
        int m = mat.size(),n = mat[0].size();
        if(m*n!=r*c)return mat;
        vector<vector<int>> ans(r,vector<int>(c));
        int x=0,y=0;
        for(int i=0;i<m;i++)
        {
            for(int j=0;j<n;j++)
            {
                if(y==c)
                {
                    x++;
                    y=0;
                }
                ans[x][y] = mat[i][j];
                y++;
            }
        }
        return ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

官方题解：

1.二维数组的一维表示

class Solution {
public:
    vector<vector<int>> matrixReshape(vector<vector<int>>& nums, int r, int c) {
        int m = nums.size();
        int n = nums[0].size();
        if (m * n != r * c) {
            return nums;
        }

        vector<vector<int>> ans(r, vector<int>(c));
        for (int x = 0; x < m * n; ++x) {
            ans[x / c][x % c] = nums[x / n][x % n];
        }
        return ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

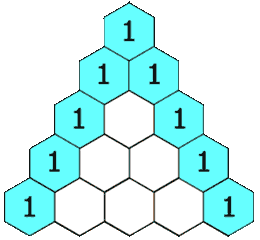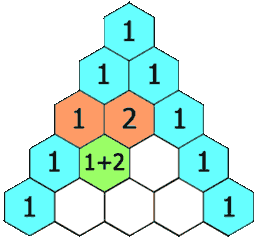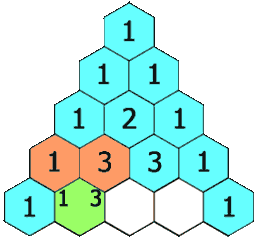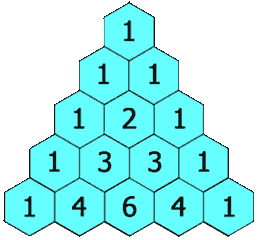
（2）118.杨辉三角

给定一个非负整数 numRows，生成「杨辉三角」的前 numRows 行。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

示例 1:

输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]
示例 2:

输入: numRows = 1
输出: [[1]]

自己的思路：写出Ann和Cnn，但是unsigened int都不够用。

官方题解：

1.数学（动态规划）

class Solution {
public:
    vector<vector<int>> generate(int numRows) {
        vector<vector<int>> ret(numRows);
        for (int i = 0; i < numRows; ++i) {
            ret[i].resize(i + 1);
            ret[i][0] = ret[i][i] = 1;
            for (int j = 1; j < i; ++j) {
                ret[i][j] = ret[i - 1][j] + ret[i - 1][j - 1];
            }
        }
        return ret;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14

要利用加法的性质，不能每一行都计算。

第五天

（1）36.有效的数独

请你判断一个 9x9 的数独是否有效。只需要根据以下规则，验证已经填入的数字是否有效即可。

数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图）
数独部分空格内已填入了数字，空白格用 ‘.’ 表示。

注意：

一个有效的数独（部分已被填充）不一定是可解的。
只需要根据以上规则，验证已经填入的数字是否有效即可。

示例 1：

输入：board =
[[“5”,“3”,“.”,“.”,“7”,“.”,“.”,“.”,“.”]
,[“6”,“.”,“.”,“1”,“9”,“5”,“.”,“.”,“.”]
,[“.”,“9”,“8”,“.”,“.”,“.”,“.”,“6”,“.”]
,[“8”,“.”,“.”,“.”,“6”,“.”,“.”,“.”,“3”]
,[“4”,“.”,“.”,“8”,“.”,“3”,“.”,“.”,“1”]
,[“7”,“.”,“.”,“.”,“2”,“.”,“.”,“.”,“6”]
,[“.”,“6”,“.”,“.”,“.”,“.”,“2”,“8”,“.”]
,[“.”,“.”,“.”,“4”,“1”,“9”,“.”,“.”,“5”]
,[“.”,“.”,“.”,“.”,“8”,“.”,“.”,“7”,“9”]]
输出：true
示例 2：

输入：board =
[[“8”,“3”,“.”,“.”,“7”,“.”,“.”,“.”,“.”]
,[“6”,“.”,“.”,“1”,“9”,“5”,“.”,“.”,“.”]
,[“.”,“9”,“8”,“.”,“.”,“.”,“.”,“6”,“.”]
,[“8”,“.”,“.”,“.”,“6”,“.”,“.”,“.”,“3”]
,[“4”,“.”,“.”,“8”,“.”,“3”,“.”,“.”,“1”]
,[“7”,“.”,“.”,“.”,“2”,“.”,“.”,“.”,“6”]
,[“.”,“6”,“.”,“.”,“.”,“.”,“2”,“8”,“.”]
,[“.”,“.”,“.”,“4”,“1”,“9”,“.”,“.”,“5”]
,[“.”,“.”,“.”,“.”,“8”,“.”,“.”,“7”,“9”]]
输出：false
解释：除了第一行的第一个数字从 5 改为 8 以外，空格内其他数字均与示例1 相同。但由于位于左上角的 3x3 宫内有两个 8 存在, 因此这个数独是无效的。

思路：分三种情况验证：

class Solution {
public:
    bool isValidSudoku(vector<vector<char>>& board) {
        //检查行
        for(int i=0;i<9;i++)
        {
            map <int,int> mp;
            for(int j=0;j<9;j++)
            {
                int a = board[i][j];
                if(a=='.')continue;
                mp[a]++;
                if(mp[a]>1)return false;
            }
            
        }
        //检查列
        for(int i=0;i<9;i++)
        {
            map <int,int> mp;
            for(int j=0;j<9;j++)
            {
                int a = board[j][i];
                if(a=='.')continue;
                mp[a]++;
                if(mp[a]>1)return false;
            }
        }
        //检查3*3
        int l = 0;
        while(l<9){
        int h =0;
        while(h<9){
        map <int ,int> mp;
        for(int i=h;i<h+3;i++)
        {
            for(int j=l;j<l+3;j++)
            {
                int a = board[i][j];
                if(a=='.')continue;
                mp[a]++;
                if(mp[a]>1)return false;
            }
        }
        h+=3;
        }
        l+=3;
        }
        return true;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

官方题解：

1.一次迭代

在这里插入图片描述

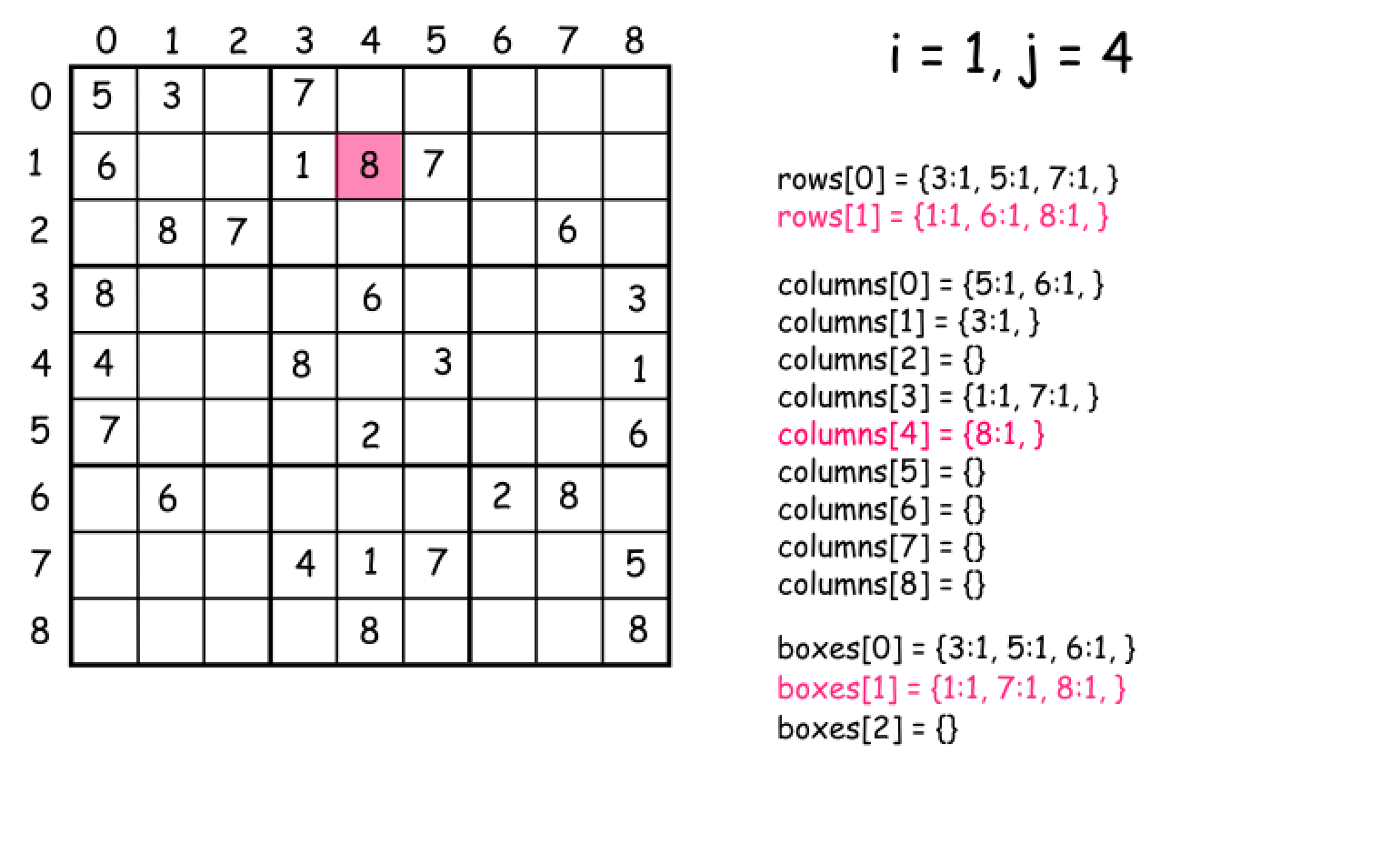
class Solution {
  public boolean isValidSudoku(char[][] board) {
    // init data
    HashMap<Integer, Integer> [] rows = new HashMap[9];
    HashMap<Integer, Integer> [] columns = new HashMap[9];
    HashMap<Integer, Integer> [] boxes = new HashMap[9];
    for (int i = 0; i < 9; i++) {
      rows[i] = new HashMap<Integer, Integer>();
      columns[i] = new HashMap<Integer, Integer>();
      boxes[i] = new HashMap<Integer, Integer>();
    }

    // validate a board
    for (int i = 0; i < 9; i++) {
      for (int j = 0; j < 9; j++) {
        char num = board[i][j];
        if (num != '.') {
          int n = (int)num;
          int box_index = (i / 3 ) * 3 + j / 3;

          // keep the current cell value
          rows[i].put(n, rows[i].getOrDefault(n, 0) + 1);
          columns[j].put(n, columns[j].getOrDefault(n, 0) + 1);
          boxes[box_index].put(n, boxes[box_index].getOrDefault(n, 0) + 1);

          // check if this value has been already seen before
          if (rows[i].get(n) > 1 || columns[j].get(n) > 1 || boxes[box_index].get(n) > 1)
            return false;
        }
      }
    }

    return true;
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

（2）73.矩阵置零

给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用原地算法。

进阶：

一个直观的解决方案是使用 O(mn) 的额外空间，但这并不是一个好的解决方案。
一个简单的改进方案是使用 O(m + n) 的额外空间，但这仍然不是最好的解决方案。
你能想出一个仅使用常量空间的解决方案吗？

示例 1：

输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出：[[1,0,1],[0,0,0],[1,0,1]]
示例 2：

输入：matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出：[[0,0,0,0],[0,4,5,0],[0,3,1,0]]

思路：直观的用一个数组存储0，然后再进行修改。

class Solution {
public:
    void setZeroes(vector<vector<int>>& matrix) {
        //直观的方法
        vector<vector<int>> ans(matrix.size(),vector<int>(matrix[0].size(),1));
        for(int i = 0 ;i<matrix.size();i++)
        {
            for(int j=0;j<matrix[0].size();j++)
            {
                if(matrix[i][j]==0)
                {
                    for(int k=0;k<matrix[0].size();k++)
                    {
                        ans[i][k] = 0;
                    }
                    for(int k=0;k<matrix.size();k++)
                    {
                        ans[k][j] = 0;
                    }
                }
            }
        }
        for(int i=0;i<matrix.size();i++)
        {
            for(int j=0;j<matrix[0].size();j++)
            {
                if(ans[i][j]==0)matrix[i][j]=0;
            }
        }
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

之前写的python3:

class Solution:
    def setZeroes(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        #总之先写一个直观的解决方案
        M, N = len(matrix), len(matrix[0])
        matrix_copy = copy.deepcopy(matrix)
        for i in range(M):
            for j in range(N):
                if matrix_copy[i][j] == 0:
                    for k in range(M):
                        matrix[k][j] = 0
                    for k in range(N):
                        matrix[i][k] = 0


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

class Solution:
    def setZeroes(self, matrix: List[List[int]]) -> None:
        M, N = len(matrix), len(matrix[0])
        row, col = set(), set() #使用set()函数，避免出现重复元素
        for i in range(M):
            for j in range(N):
                if matrix[i][j] == 0:
                    row.add(i)
                    col.add(j)
        for i in range(M):
            for j in range(N):
                if i in row or j in col:
                    matrix[i][j] = 0
1
2
3
4
5
6
7
8
9
10
11
12
13

官方题解：

1.使用标记数组

使用了bool数组的方法。

2.使用两个标记变量

我们可以用矩阵的第一行和第一列代替方法一中的两个标记数组，以达到 O(1) 的额外空间。但这样会导致原数组的第一行和第一列被修改，无法记录它们是否原本包含 0。因此我们需要额外使用两个标记变量分别记录第一行和第一列是否原本包含 0。

在实际代码中，我们首先预处理出两个标记变量，接着使用其他行与列去处理第一行与第一列，然后反过来使用第一行与第一列去更新其他行与列，最后使用两个标记变量更新第一行与第一列即可。

//机智的方法，减少空间的利用

class Solution {
public:
    void setZeroes(vector<vector<int>>& matrix) {
        int m = matrix.size();
        int n = matrix[0].size();
        int flag_col0 = false, flag_row0 = false;
        for (int i = 0; i < m; i++) {
            if (!matrix[i][0]) {
                flag_col0 = true;
            }
        }
        for (int j = 0; j < n; j++) {
            if (!matrix[0][j]) {
                flag_row0 = true;
            }
        }
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (!matrix[i][j]) {
                    matrix[i][0] = matrix[0][j] = 0;
                }
            }
        }
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (!matrix[i][0] || !matrix[0][j]) {
                    matrix[i][j] = 0;
                }
            }
        }
        if (flag_col0) {
            for (int i = 0; i < m; i++) {
                matrix[i][0] = 0;
            }
        }
        if (flag_row0) {
            for (int j = 0; j < n; j++) {
                matrix[0][j] = 0;
            }
        }
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

3.使用一个标记变量

我们可以对方法二进一步优化，只使用一个标记变量记录第一列是否原本存在 0。这样，第一列的第一个元素即可以标记第一行是否出现 0。但为了防止每一列的第一个元素被提前更新，我们需要从最后一行开始，倒序地处理矩阵元素。

//程序员什么都想的出来啊【躺】

class Solution {
public:
    void setZeroes(vector<vector<int>>& matrix) {
        int m = matrix.size();
        int n = matrix[0].size();
        int flag_col0 = false;
        for (int i = 0; i < m; i++) {
            if (!matrix[i][0]) {
                flag_col0 = true;
            }
            for (int j = 1; j < n; j++) {
                if (!matrix[i][j]) {
                    matrix[i][0] = matrix[0][j] = 0;
                }
            }
        }
        for (int i = m - 1; i >= 0; i--) {
            for (int j = 1; j < n; j++) {
                if (!matrix[i][0] || !matrix[0][j]) {
                    matrix[i][j] = 0;
                }
            }
            if (flag_col0) {
                matrix[i][0] = 0;
            }
        }
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

第六天

（1）387.字符串中的第一个唯一字符

给定一个字符串，找到它的第一个不重复的字符，并返回它的索引。如果不存在，则返回 -1。

示例：

s = “leetcode”
返回 0

s = “loveleetcode”
返回 2

思路：建立字母与个数的组找出第一个为1的，没有就返回-1

class Solution {
public:
    int firstUniqChar(string s) {
        vector<int> mp(26);
        for(int i=0;i<s.size();i++)
        {
            mp[s[i]-'a']++;
        }
        int point = 0;
        for(int i=0;i<s.size();i++)
        {
            if(mp[s[i]-'a']==1)return point;
            point++;
        }
        return -1;

    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

int firstUniqChar(char * s){
    int a[26];
    int i;
    for(i=0;i<26;i++){
        a[i]=0;
    }
    for(i=0;s[i]!='\0';i++){
        a[s[i]-'a']++;
    }
    for(i=0;s[i]!='\0';i++){
        if(a[s[i]-'a']==1)return i;
    }
    return -1;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

//这个c比c++要优，不是很懂为什么

官方题解：

1.使用哈希表存储频数

是爷的思路没错。

2.使用哈希表存储索引

我们可以对方法一进行修改，使得第二次遍历的对象从字符串变为哈希映射。

具体地，对于哈希映射中的每一个键值对，键表示一个字符，值表示它的首次出现的索引（如果该字符只出现一次）或者 -1（如果该字符出现多次）。当我们第一次遍历字符串时，设当前遍历到的字符为 c，如果 c 不在哈希映射中，我们就将 c 与它的索引作为一个键值对加入哈希映射中，否则我们将 cc 在哈希映射中对应的值修改为 -1。

在第一次遍历结束后，我们只需要再遍历一次哈希映射中的所有值，找出其中不为 −1 的最小值，即为第一个不重复字符的索引。如果哈希映射中的所有值均为 -1，我们就返回 -1。

class Solution {
public:
    int firstUniqChar(string s) {
        unordered_map<int, int> position;
        int n = s.size();
        for (int i = 0; i < n; ++i) {
            if (position.count(s[i])) {
                position[s[i]] = -1;
            }
            else {
                position[s[i]] = i;
            }
        }
        int first = n;
        for (auto [_, pos]: position) {
            if (pos != -1 && pos < first) {
                first = pos;
            }
        }
        if (first == n) {
            first = -1;
        }
        return first;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

3.队列

我们也可以借助队列找到第一个不重复的字符。队列具有「先进先出」的性质，因此很适合用来找出第一个满足某个条件的元素。

具体地，我们使用与方法二相同的哈希映射，并且使用一个额外的队列，按照顺序存储每一个字符以及它们第一次出现的位置。当我们对字符串进行遍历时，设当前遍历到的字符为 c，如果 c 不在哈希映射中，我们就将 c 与它的索引作为一个二元组放入队尾，否则我们就需要检查队列中的元素是否都满足「只出现一次」的要求，即我们不断地根据哈希映射中存储的值（是否为 -1）选择弹出队首的元素，直到队首元素「真的」只出现了一次或者队列为空。

在遍历完成后，如果队列为空，说明没有不重复的字符，返回 -1，否则队首的元素即为第一个不重复的字符以及其索引的二元组。

小贴士

在维护队列时，我们使用了「延迟删除」这一技巧。也就是说，即使队列中有一些字符出现了超过一次，但它只要不位于队首，那么就不会对答案造成影响，我们也就可以不用去删除它。只有当它前面的所有字符被移出队列，它成为队首时，我们才需要将它移除。

class Solution {
public:
    int firstUniqChar(string s) {
        unordered_map<char, int> position;
        queue<pair<char, int>> q;
        int n = s.size();
        for (int i = 0; i < n; ++i) {
            if (!position.count(s[i])) {
                position[s[i]] = i;
                q.emplace(s[i], i);
            }
            else {
                position[s[i]] = -1;
                while (!q.empty() && position[q.front().first] == -1) {
                    q.pop();
                }
            }
        }
        return q.empty() ? -1 : q.front().second;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

（2）383.赎金信

给定一个赎金信 (ransom) 字符串和一个杂志(magazine)字符串，判断第一个字符串 ransom 能不能由第二个字符串 magazines 里面的字符构成。如果可以构成，返回 true ；否则返回 false。

(题目说明：为了不暴露赎金信字迹，要从杂志上搜索各个需要的字母，组成单词来表达意思。杂志字符串中的每个字符只能在赎金信字符串中使用一次。)

示例 1：

输入：ransomNote = “a”, magazine = “b”
输出：false

示例 2：

输入：ransomNote = “aa”, magazine = “ab”
输出：false

示例 3：

输入：ransomNote = “aa”, magazine = “aab”
输出：true

思路：存储有的字母的个数，然后对应赎金信如果没有就是false

class Solution {
public:
    bool canConstruct(string ransomNote, string magazine) {
        vector<int> mp(26,0);
        for(char a:magazine)mp[a-'a']++;
        for(char a:ransomNote)
        {
            mp[a-'a']--;
            if(mp[a-'a']<0)return false;
        }
        return true;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13

官方题解【无】

取巧：string的find()

class Solution {
public:
    bool canConstruct(string ransomNote, string magazine) {
        for(int i = 0; i < ransomNote.size(); i++){
            int a = magazine.find(ransomNote[i]);
            if(a != -1){
                magazine[a] = '0';
            }else{
                return false;
            }
        }
        return true;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14

s.find(s[i]) : 返回字符串s中从左向右查找s[i]第一次出现的位置；
题目中已说明两个字符串均只含小写字母，因此，只需在magazine字符串中检索ransomNote字符串中的每一个字符，magazine中检索过的字符进行标记即可。
作者：best-jin-xing-shi-k

（3）242.有效的字母异位词

给定两个字符串 s 和 t ，编写一个函数来判断 t 是否是 s 的字母异位词。

注意：若 s 和 t 中每个字符出现的次数都相同，则称 s 和 t 互为字母异位词。

示例 1:

输入: s = “anagram”, t = “nagaram”
输出: true

示例 2:

输入: s = “rat”, t = “car”
输出: false

思路：同上题

class Solution {
public:
    bool isAnagram(string s, string t) {
        if(s.size()!=t.size())return false;
        //和本计划上一个题一个思路
        vector<int> mp(26,0);
        for(char a : s)mp[a-'a']++;
        for(char a : t)
        {
            mp[a-'a']--;
            if(mp[a-'a']<0)return false;
        }
        return true;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

官方题解：

1.排序

条件==排序后相等

class Solution {
public:
    bool isAnagram(string s, string t) {
        if (s.length() != t.length()) {
            return false;
        }
        sort(s.begin(), s.end());
        sort(t.begin(), t.end());
        return s == t;
    }
};
1
2
3
4
5
6
7
8
9
10
11

2.哈希表

爷的方法，对于unicode字符：

class Solution {
    public boolean isAnagram(String s, String t) {
        if (s.length() != t.length()) {
            return false;
        }
        Map<Character, Integer> table = new HashMap<Character, Integer>();
        for (int i = 0; i < s.length(); i++) {
            char ch = s.charAt(i);
            table.put(ch, table.getOrDefault(ch, 0) + 1);
        }
        for (int i = 0; i < t.length(); i++) {
            char ch = t.charAt(i);
            table.put(ch, table.getOrDefault(ch, 0) - 1);
            if (table.get(ch) < 0) {
                return false;
            }
        }
        return true;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

func isAnagram(s, t string) bool {
    if len(s) != len(t) {
        return false
    }
    cnt := map[rune]int{}
    for _, ch := range s {
        cnt[ch]++
    }
    for _, ch := range t {
        cnt[ch]--
        if cnt[ch] < 0 {
            return false
        }
    }
    return true
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

第七天

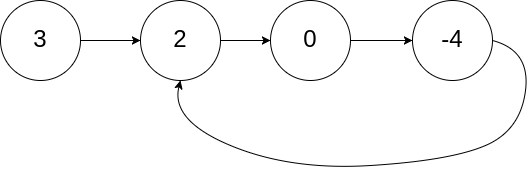
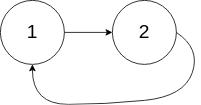
（1）141.环形链表

给定一个链表，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

如果链表中存在环，则返回 true 。否则，返回 false 。

进阶：

你能用 O(1)（即，常量）内存解决此问题吗？

示例 1：

输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。
示例 2：

输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。
示例 3：

输入：head = [1], pos = -1
输出：false
解释：链表中没有环。

思路：求环经典快慢指针：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    bool hasCycle(ListNode *head) {
        //双指针经典问题
        ListNode *l,*r;
        l = head;
        r = head;
        while(l!=NULL&&r!=NULL)
        {
            l = l->next;
            r = r->next;
            if(r!=NULL)r = r->next;
            if(l==r&&r!=NULL)return true;
        }
        return false;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

官方题解：

1.哈希表

class Solution {
public:
    bool hasCycle(ListNode *head) {
        unordered_set<ListNode*> seen;
        while (head != nullptr) {
            if (seen.count(head)) {
                return true;
            }
            seen.insert(head);
            head = head->next;
        }
        return false;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14

2.快慢指针

「Floyd 判圈算法」（又称龟兔赛跑算法）

与本人算法有出入，但我的也过了。比较有趣：

class Solution {
public:
    bool hasCycle(ListNode* head) {
        if (head == nullptr || head->next == nullptr) {
            return false;
        }
        ListNode* slow = head;
        ListNode* fast = head->next;
        while (slow != fast) {
            if (fast == nullptr || fast->next == nullptr) {
                return false;
            }
            slow = slow->next;
            fast = fast->next->next;
        }
        return true;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

冲突：
在这里插入图片描述

（2）21.合并两个有序链表

将两个升序链表合并为一个新的升序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

示例 1：

输入：l1 = [1,2,4], l2 = [1,3,4]
输出：[1,1,2,3,4,4]
示例 2：

输入：l1 = [], l2 = []
输出：[]
示例 3：

输入：l1 = [], l2 = [0]
输出：[0]

思路：遍历插入，应该就是考察链表的结构：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
        //经典双指针
        if(l1==nullptr&&l2==nullptr)return l1;
        else if(l1==nullptr&&l2!=nullptr)return l2;
        else if(l1!=nullptr&&l2==nullptr)return l1;
        if(l1->val>l2->val)
        {
            ListNode *temp = l1;
            l1 = l2;
            l2 = temp;
        }
        ListNode *head = l1;
        ListNode *pre = l1;
        while(l1!=nullptr&&l2!=nullptr)
        {
        if(l1->val>l2->val)
        {
            pre->next = l2;
            ListNode *temp = l1;
            l1 = l2;
            l2 = temp;
        }
        else 
        {
           if(l1->next!=nullptr)
           {
               pre = l1;
               l1 = l1->next;
           }
           else 
           {
               l1->next = l2;
               break;
           }
        }
         
        }
        return head;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

官方题解：

1.递归

在这里插入图片描述

递归我是真没想到，主要这个空指针就返回还有交换l1和l2的顺序比较有趣，看代码根本看不懂TUT

class Solution {
public:
    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
        if (l1 == nullptr) {
            return l2;
        } else if (l2 == nullptr) {
            return l1;
        } else if (l1->val < l2->val) {
            l1->next = mergeTwoLists(l1->next, l2);
            return l1;
        } else {
            l2->next = mergeTwoLists(l1, l2->next);
            return l2;
        }
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

2.迭代

我的思路

（3）移除链表元素

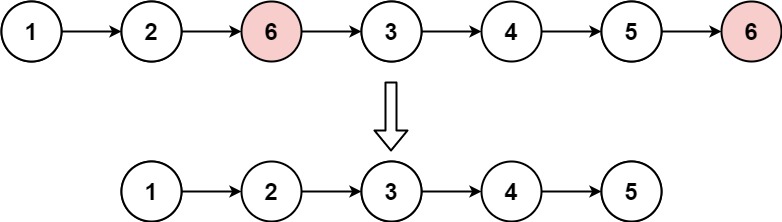
给你一个链表的头节点 head 和一个整数 val ，请你删除链表中所有满足 Node.val == val 的节点，并返回新的头节点。

示例 1：

输入：head = [1,2,6,3,4,5,6], val = 6
输出：[1,2,3,4,5]
示例 2：

输入：head = [], val = 1
输出：[]
示例 3：

输入：head = [7,7,7,7], val = 7
输出：[]

思路：遍历，删除，注意头节点被删除的情况

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* removeElements(ListNode* head, int val) {
        if(head==nullptr)return head;
    
        while(head!=nullptr&&head->val==val)head = head->next;
        
        ListNode *p = head;
        ListNode *pre = head;
        while(p!=nullptr)
        {
            while(p!=nullptr&&p->val==val)
            {
                ListNode *temp = p->next;
                pre->next = temp;
                p = p->next;
            }
            if(p!=nullptr)
            {
                pre = p;
                p = p->next;
            }
        }
        return head;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

官方题解：

1.递归

在这里插入图片描述

链表题注意使用递归

class Solution {
public:
    ListNode* removeElements(ListNode* head, int val) {
        if (head == nullptr) {
            return head;
        }
        head->next = removeElements(head->next, val);
        return head->val == val ? head->next : head;
    }
};
1
2
3
4
5
6
7
8
9
10

2.迭代

同爷的思路，但代码简洁：

class Solution {
public:
    ListNode* removeElements(ListNode* head, int val) {
        struct ListNode* dummyHead = new ListNode(0, head);
        struct ListNode* temp = dummyHead;
        while (temp->next != NULL) {
            if (temp->next->val == val) {
                temp->next = temp->next->next;
            } else {
                temp = temp->next;
            }
        }
        return dummyHead->next;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

第八天

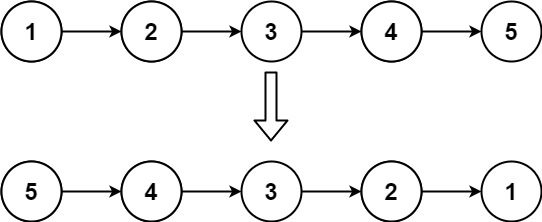
（1）206.反转链表

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

示例 1：

输入：head = [1,2,3,4,5]
输出：[5,4,3,2,1]
示例 2：

输入：head = [1,2]
输出：[2,1]
示例 3：

输入：head = []
输出：[]

思路：存储反转再覆盖

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        //迭代
        if(head==nullptr)return head;
        ListNode *ans = head;
        //最简单的思路是存储后再创建
        vector<int> mp;
        while(head!=nullptr)
        {
            mp.push_back(head->val);
            head = head->next;
        }
        reverse(mp.begin(),mp.end());
        head = ans;
        int i = 0;
        while(head!=nullptr)
        {
            head->val = mp[i];
            i++;
            head = head->next;
        }
        return ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

官方题解：

1.迭代

假设链表为 1→2→3→∅，我们想要把它改成∅←1←2←3。

在遍历链表时，将当前节点的 next 指针改为指向前一个节点。由于节点没有引用其前一个节点，因此必须事先存储其前一个节点。在更改引用之前，还需要存储后一个节点。最后返回新的头引用。

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        ListNode* prev = nullptr;
        ListNode* curr = head;
        while (curr) {
            ListNode* next = curr->next;
            curr->next = prev;
            prev = curr;
            curr = next;
        }
        return prev;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14

2.递归

在这里插入图片描述

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        if (!head || !head->next) {
            return head;
        }
        ListNode* newHead = reverseList(head->next);
        head->next->next = head;
        head->next = nullptr;
        return newHead;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12

（2）83.删除排序链表中的重复元素

存在一个按升序排列的链表，给你这个链表的头节点 head ，请你删除所有重复的元素，使每个元素只出现一次。

返回同样按升序排列的结果链表。

示例 1：

输入：head = [1,1,2]
输出：[1,2]
示例 2：

输入：head = [1,1,2,3,3]
输出：[1,2,3]

思路：已经排好序只需要比较前后就可以了，不相同就把head后移

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* deleteDuplicates(ListNode* head) {
        ListNode *ans = head;
        while(head!=nullptr)
        {
            if(head->next!=nullptr&&head->next->val==head->val)
            {
                head->next = head->next->next;
            }
            else if(head!=nullptr)head = head->next;
        }
        return ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

官方题解：

1.一次遍历

思路相同

第九天

（1）20.有效的括号

给定一个只包括 ‘(’，‘)’，‘{’，‘}’，‘[’，‘]’ 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。

示例 1：

输入：s = “()”
输出：true
示例 2：

输入：s = “()[]{}”
输出：true
示例 3：

输入：s = “(]”
输出：false
示例 4：

输入：s = “([)]”
输出：false
示例 5：

输入：s = “{[]}”
输出：true

思路：找反括号前的第一个正括号判断是否配队，记得特殊情况特殊讨论

class Solution {
public:
    bool isValid(string s) {
        if(s.size()==1)return false;
        vector<char> q;
        for(char c:s)
        {
            if(c=='('||c=='{'||c=='[')q.push_back(c);
            else
            {
                if(q.empty())return false;
                char a = q.back();
                if(c==')'&&a!='(')return false;
                else if(c=='}'&&a!='{')return false;
                else if(c==']'&&a!='[')return false;
                q.erase(q.end()-1);
            }
        }
        if(q.empty())return true;
        else return false;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

官方题解：

1.栈

判断括号的有效性可以使用「栈」这一数据结构来解决。

我们遍历给定的字符串 s。当我们遇到一个左括号时，我们会期望在后续的遍历中，有一个相同类型的右括号将其闭合。由于后遇到的左括号要先闭合，因此我们可以将这个左括号放入栈顶。

当我们遇到一个右括号时，我们需要将一个相同类型的左括号闭合。此时，我们可以取出栈顶的左括号并判断它们是否是相同类型的括号。如果不是相同的类型，或者栈中并没有左括号，那么字符串 s 无效，返回 False。为了快速判断括号的类型，我们可以使用哈希表存储每一种括号。哈希表的键为右括号，值为相同类型的左括号。

在遍历结束后，如果栈中没有左括号，说明我们将字符串 s中的所有左括号闭合，返回 True，否则返回 False。

注意到有效字符串的长度一定为偶数，因此如果字符串的长度为奇数，我们可以直接返回 False，省去后续的遍历判断过程。

class Solution {
public:
    bool isValid(string s) {
        int n = s.size();
        if (n % 2 == 1) {
            return false;
        }

        unordered_map<char, char> pairs = {
            {')', '('},
            {']', '['},
            {'}', '{'}
        };
        stack<char> stk;
        for (char ch: s) {
            if (pairs.count(ch)) {
                if (stk.empty() || stk.top() != pairs[ch]) {
                    return false;
                }
                stk.pop();
            }
            else {
                stk.push(ch);
            }
        }
        return stk.empty();
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

（2）232.用栈实现队列

请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）：

实现 MyQueue 类：

void push(int x) 将元素 x 推到队列的末尾
int pop() 从队列的开头移除并返回元素
int peek() 返回队列开头的元素
boolean empty() 如果队列为空，返回 true ；否则，返回 false

说明：

你只能使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
你所使用的语言也许不支持栈。你可以使用 list 或者 deque（双端队列）来模拟一个栈，只要是标准的栈操作即可。

进阶：

你能否实现每个操作均摊时间复杂度为 O(1) 的队列？换句话说，执行 n 个操作的总时间复杂度为 O(n) ，即使其中一个操作可能花费较长时间。

示例：

输入：
[“MyQueue”, “push”, “push”, “peek”, “pop”, “empty”]
[[], [1], [2], [], [], []]
输出：
[null, null, null, 1, 1, false]

解释：
MyQueue myQueue = new MyQueue();
myQueue.push(1); // queue is: [1]
myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue)
myQueue.peek(); // return 1
myQueue.pop(); // return 1, queue is [2]
myQueue.empty(); // return false

思路：循环遍历找队首

class MyQueue {
public:
    stack<int> s;
    /** Initialize your data structure here. */
    MyQueue() {
        
    }
    
    /** Push element x to the back of queue. */
    void push(int x) {
        s.push(x);
    }
    
    /** Removes the element from in front of queue and returns that element. */
    int pop() {
        stack<int> s2;
        while(!s.empty())
        {
            int a = s.top();
            s.pop();
            s2.push(a);
        }
        
        int ans = s2.top();
        s2.pop();

        while(!s2.empty())
        {
            int a = s2.top();
            s2.pop();
            s.push(a);
        }
        return ans;
    }
    
    /** Get the front element. */
    int peek() {
        stack<int> s2;
        while(!s.empty())
        {
            int a = s.top();
            s.pop();
            s2.push(a);
        }
        
        int ans = s2.top();

        while(!s2.empty())
        {
            int a = s2.top();
            s2.pop();
            s.push(a);
        }
        return ans;
    }
    
    /** Returns whether the queue is empty. */
    bool empty() {
        return s.empty();
    }
};

/**
 * Your MyQueue object will be instantiated and called as such:
 * MyQueue* obj = new MyQueue();
 * obj->push(x);
 * int param_2 = obj->pop();
 * int param_3 = obj->peek();
 * bool param_4 = obj->empty();
 */
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70

官方题解：

1.双栈

将一个栈当作输入栈，用于压入push 传入的数据；另一个栈当作输出栈，用于 pop 和 peek 操作。

每次 pop 或 peek 时，若输出栈为空则将输入栈的全部数据依次弹出并压入输出栈，这样输出栈从栈顶往栈底的顺序就是队列从队首往队尾的顺序。

class MyQueue {
private:
    stack<int> inStack, outStack;

    void in2out() {
        while (!inStack.empty()) {
            outStack.push(inStack.top());
            inStack.pop();
        }
    }

public:
    MyQueue() {}

    void push(int x) {
        inStack.push(x);
    }

    int pop() {
        if (outStack.empty()) {
            in2out();
        }
        int x = outStack.top();
        outStack.pop();
        return x;
    }

    int peek() {
        if (outStack.empty()) {
            in2out();
        }
        return outStack.top();
    }

    bool empty() {
        return inStack.empty() && outStack.empty();
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

第十天

（1）144.二叉树的前序遍历

给你二叉树的根节点 root ，返回它节点值的前序遍历。

示例 1：

输入：root = [1,null,2,3]
输出：[1,2,3]
示例 2：

输入：root = []
输出：[]
示例 3：

输入：root = [1]
输出：[1]
示例 4：

输入：root = [1,2]
输出：[1,2]
示例 5：

输入：root = [1,null,2]
输出：[1,2]

提示：

树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100

进阶：递归算法很简单，你可以通过迭代算法完成吗？

思考半天容器怎么传递的问题，最后用循环做了，感觉很蠢

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
    //前序：先左后右
    //递归
    vector<int> ans;
    if(root!=nullptr)
    {
    ans.push_back(root->val);
    if(root->left)
    {
        vector<int> cur = preorderTraversal(root->left);
        for(int i=0;i<cur.size();i++)
        {
            ans.push_back(cur[i]);
        }
    }
    if(root->right)
    {
        vector<int> cur = preorderTraversal(root->right);
        for(int i=0;i<cur.size();i++)
        {
            ans.push_back(cur[i]);
        }
    }
    }
    return ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

官方题解：

1.递归

class Solution {
public:
    void preorder(TreeNode *root, vector<int> &res) {
        if (root == nullptr) {
            return;
        }
        res.push_back(root->val);
        preorder(root->left, res);
        preorder(root->right, res);
    }

    vector<int> preorderTraversal(TreeNode *root) {
        vector<int> res;
        preorder(root, res);
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

在原函数基础上重写了一个需要传递容器的函数解决了传递问题TUT

2.迭代

我们也可以用迭代的方式实现方法一的递归函数，两种方式是等价的，区别在于递归的时候隐式地维护了一个栈，而我们在迭代的时候需要显式地将这个栈模拟出来，其余的实现与细节都相同，具体可以参考下面的代码。

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> res;
        if (root == nullptr) {
            return res;
        }

        stack<TreeNode*> stk;//显式的栈
        TreeNode* node = root;
        while (!stk.empty() || node != nullptr) {
            while (node != nullptr) {
                res.emplace_back(node->val);
                stk.emplace(node);
                node = node->left;
            }
            node = stk.top();
            stk.pop();
            node = node->right;
        }
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

3.Morris遍历

有一种巧妙的方法可以在线性时间内，只占用常数空间来实现前序遍历。这种方法由 J. H. Morris 在 1979 年的论文「Traversing Binary Trees Simply and Cheaply」中首次提出，因此被称为 Morris 遍历。

Morris 遍历的核心思想是利用树的大量空闲指针，实现空间开销的极限缩减。其前序遍历规则总结如下：

新建临时节点，令该节点为 root；
如果当前节点的左子节点为空，将当前节点加入答案，并遍历当前节点的右子节点；
如果当前节点的左子节点不为空，在当前节点的左子树中找到当前节点在中序遍历下的前驱节点：
- 如果前驱节点的右子节点为空，将前驱节点的右子节点设置为当前节点。然后将当前节点加入答案，并将前驱节点的右子节点更新为当前节点。当前节点更新为当前节点的左子节点。
- 如果前驱节点的右子节点为当前节点，将它的右子节点重新设为空。当前节点更新为当前节点的右子节点。
重复步骤 2 和步骤 3，直到遍历结束。

这样我们利用 Morris 遍历的方法，前序遍历该二叉树，即可实现线性时间与常数空间的遍历。

class Solution {
public:
    vector<int> preorderTraversal(TreeNode *root) {
        vector<int> res;
        if (root == nullptr) {
            return res;
        }

        TreeNode *p1 = root, *p2 = nullptr;

        while (p1 != nullptr) {
            p2 = p1->left;
            if (p2 != nullptr) {
                while (p2->right != nullptr && p2->right != p1) {
                    p2 = p2->right;
                }
                if (p2->right == nullptr) {
                    res.emplace_back(p1->val);
                    p2->right = p1;
                    p1 = p1->left;
                    continue;
                } else {
                    p2->right = nullptr;
                }
            } else {
                res.emplace_back(p1->val);
            }
            p1 = p1->right;
        }
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

关于emplace_back():C++ STL vector添加元素（push_back()和emplace_back()）详解 (biancheng.net)

（2）94.二叉树的中序遍历

给定一个二叉树的根节点 root ，返回它的中序遍历。

示例 1：

输入：root = [1,null,2,3]
输出：[1,3,2]
示例 2：

输入：root = []
输出：[]
示例 3：

输入：root = [1]
输出：[1]
示例 4：

输入：root = [1,2]
输出：[2,1]
示例 5：

输入：root = [1,null,2]
输出：[1,2]

提示：

树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100

进阶: 递归算法很简单，你可以通过迭代算法完成吗？

这三道题都是第一题的模板直接写的：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ans;
        if(root==nullptr)return ans;
        if(root->left)
        {
            vector <int> cur = inorderTraversal(root->left);
            for(int i=0;i<cur.size();i++)ans.push_back(cur[i]);
        }
        ans.push_back(root->val);
        if(root->right)
        {
            vector<int> cur = inorderTraversal(root->right);
            for(int i=0;i<cur.size();i++)ans.push_back(cur[i]);
        }
        return ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

官方题解：

1.递归

class Solution {
public:
    void inorder(TreeNode* root, vector<int>& res) {
        if (!root) {
            return;
        }
        inorder(root->left, res);
        res.push_back(root->val);
        inorder(root->right, res);
    }
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        inorder(root, res);
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

2.迭代

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        stack<TreeNode*> stk;
        while (root != nullptr || !stk.empty()) {
            while (root != nullptr) {
                stk.push(root);
                root = root->left;
            }
            root = stk.top();
            stk.pop();
            res.push_back(root->val);
            root = root->right;
        }
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

3.Morris中序遍历

在这里插入图片描述
其实整个过程我们就多做一步：假设当前遍历到的节点为 x，将 x 的左子树中最右边的节点的右孩子指向 x，这样在左子树遍历完成后我们通过这个指向走回了 x，且能通过这个指向知晓我们已经遍历完成了左子树，而不用再通过栈来维护，省去了栈的空间复杂度。

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        TreeNode *predecessor = nullptr;

        while (root != nullptr) {
            if (root->left != nullptr) {
                // predecessor 节点就是当前 root 节点向左走一步，然后一直向右走至无法走为止
                predecessor = root->left;
                while (predecessor->right != nullptr && predecessor->right != root) {
                    predecessor = predecessor->right;
                }
                
                // 让 predecessor 的右指针指向 root，继续遍历左子树
                if (predecessor->right == nullptr) {
                    predecessor->right = root;
                    root = root->left;
                }
                // 说明左子树已经访问完了，我们需要断开链接
                else {
                    res.push_back(root->val);
                    predecessor->right = nullptr;
                    root = root->right;
                }
            }
            // 如果没有左孩子，则直接访问右孩子
            else {
                res.push_back(root->val);
                root = root->right;
            }
        }
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

（3）145.二叉树的后序遍历

给定一个二叉树，返回它的后序遍历。

示例:

输入: [1,null,2,3]
1

2
/
3

输出: [3,2,1]
进阶: 递归算法很简单，你可以通过迭代算法完成吗？

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
         vector<int> ans;
        if(root==nullptr)return ans; 
         if(root->left)
        {
            vector<int> cur = postorderTraversal(root->left);
            for(int i=0;i<cur.size();i++)ans.push_back(cur[i]);
        }
        if(root->right)
        {
            vector <int> cur = postorderTraversal(root->right);
            for(int i=0;i<cur.size();i++)ans.push_back(cur[i]);
        }
        ans.push_back(root->val);
        return ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

官方题解：

1.递归

class Solution {
public:
    void postorder(TreeNode *root, vector<int> &res) {
        if (root == nullptr) {
            return;
        }
        postorder(root->left, res);
        postorder(root->right, res);
        res.push_back(root->val);
    }

    vector<int> postorderTraversal(TreeNode *root) {
        vector<int> res;
        postorder(root, res);
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

2.迭代

class Solution {
public:
    vector<int> postorderTraversal(TreeNode *root) {
        vector<int> res;
        if (root == nullptr) {
            return res;
        }

        stack<TreeNode *> stk;
        TreeNode *prev = nullptr;
        while (root != nullptr || !stk.empty()) {
            while (root != nullptr) {
                stk.emplace(root);
                root = root->left;
            }
            root = stk.top();
            stk.pop();
            if (root->right == nullptr || root->right == prev) {
                res.emplace_back(root->val);
                prev = root;
                root = nullptr;
            } else {
                stk.emplace(root);
                root = root->right;
            }
        }
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

3.Morris遍历

有一种巧妙的方法可以在线性时间内，只占用常数空间来实现后序遍历。这种方法由 J. H. Morris 在 1979 年的论文「Traversing Binary Trees Simply and Cheaply」中首次提出，因此被称为 Morris 遍历。

Morris 遍历的核心思想是利用树的大量空闲指针，实现空间开销的极限缩减。其后序遍历规则总结如下：

新建临时节点，令该节点为 root；
如果当前节点的左子节点为空，则遍历当前节点的右子节点；
如果当前节点的左子节点不为空，在当前节点的左子树中找到当前节点在中序遍历下的前驱节点；
- 如果前驱节点的右子节点为空，将前驱节点的右子节点设置为当前节点，当前节点更新为当前节点的左子节点。
- 如果前驱节点的右子节点为当前节点，将它的右子节点重新设为空。倒序输出从当前节点的左子节点到该前驱节点这条路径上的所有节点。当前节点更新为当前节点的右子节点。
重复步骤 2 和步骤 3，直到遍历结束。

这样我们利用 Morris 遍历的方法，后序遍历该二叉搜索树，即可实现线性时间与常数空间的遍历。

class Solution {
public:
    void addPath(vector<int> &vec, TreeNode *node) {
        int count = 0;
        while (node != nullptr) {
            ++count;
            vec.emplace_back(node->val);
            node = node->right;
        }
        reverse(vec.end() - count, vec.end());
    }

    vector<int> postorderTraversal(TreeNode *root) {
        vector<int> res;
        if (root == nullptr) {
            return res;
        }

        TreeNode *p1 = root, *p2 = nullptr;

        while (p1 != nullptr) {
            p2 = p1->left;
            if (p2 != nullptr) {
                while (p2->right != nullptr && p2->right != p1) {
                    p2 = p2->right;
                }
                if (p2->right == nullptr) {
                    p2->right = p1;
                    p1 = p1->left;
                    continue;
                } else {
                    p2->right = nullptr;
                    addPath(res, p1->left);
                }
            }
            p1 = p1->right;
        }
        addPath(res, root);
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

第十一天

（1）102.二叉树的层序遍历

102. 二叉树的层序遍历

难度中等982收藏分享切换为英文接收动态反馈

给你一个二叉树，请你返回其按 层序遍历 得到的节点值。（即逐层地，从左到右访问所有节点）。

示例：
二叉树：[3,9,20,null,null,15,7],
 3/ \9  20 /  \15   7
1
返回其层序遍历结果：
[[3],[9,20],[15,7]]
1

没有思路呜呜

官方题解：

1.广度优先搜索

队列的巧妙应用算法的证明

在这里插入图片描述

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector <vector <int>> ret;
        if (!root) {
            return ret;
        }

        queue <TreeNode*> q;
        q.push(root);
        while (!q.empty()) {
            int currentLevelSize = q.size();
            ret.push_back(vector <int> ());
            for (int i = 1; i <= currentLevelSize; ++i) {
                auto node = q.front(); q.pop();
                ret.back().push_back(node->val);
                if (node->left) q.push(node->left);
                if (node->right) q.push(node->right);
            }
        }
        
        return ret;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

看完题解写的：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
       vector<vector<int>> ans;
       if(!root)return ans;
       queue<TreeNode*> list;
       list.push(root);
       while(!list.empty())
       {
           int size = list.size();
           vector<int> temp;
           for(int i=1;i<=size;i++)
           {
               auto node = list.front();
               temp.push_back(node->val);
               list.pop();
               //取出当前节点并抛弃，存入下两个结点，i保证存入每个结点
               if(node->left)list.push(node->left);
               if(node->right)list.push(node->right);
           }
           ans.push_back(temp);
       }
          return ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

（2）104.二叉树的最大深度

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：
给定二叉树 [3,9,20,null,null,15,7]，
 3/ \9  20 /  \15   7
1

不会。。。

官方题解：

1.深度优先算法

如果我们知道了左子树和右子树的最大深度 l 和 r，那么该二叉树的最大深度即为 max(l,r)+1

而左子树和右子树的最大深度又可以以同样的方式进行计算。因此我们可以用「深度优先搜索」的方法来计算二叉树的最大深度。具体而言，在计算当前二叉树的最大深度时，可以先递归计算出其左子树和右子树的最大深度，然后在 O(1) 时间内计算出当前二叉树的最大深度。递归在访问到空节点时退出。

class Solution {
public:
    int maxDepth(TreeNode* root) {
        if (root == nullptr) return 0;
        return max(maxDepth(root->left), maxDepth(root->right)) + 1;
        //想左找的最大值和向右找的最大值比较，这个+1是每一次返回都加，也就是层数了
    }
};
1
2
3
4
5
6
7
8

2.广度优先搜索

我们也可以用「广度优先搜索」的方法来解决这道题目，但我们需要对其进行一些修改，此时我们广度优先搜索的队列里存放的是「当前层的所有节点」。每次拓展下一层的时候，不同于广度优先搜索的每次只从队列里拿出一个节点，我们需要将队列里的所有节点都拿出来进行拓展，这样能保证每次拓展完的时候队列里存放的是当前层的所有节点，即我们是一层一层地进行拓展，最后我们用一个变量 ans 来维护拓展的次数，该二叉树的最大深度即为 ans。

class Solution {
public:
    int maxDepth(TreeNode* root) {
        if (root == nullptr) return 0;
        queue<TreeNode*> Q;
        Q.push(root);
        int ans = 0;
        while (!Q.empty()) {
            int sz = Q.size();
            while (sz > 0) {
                TreeNode* node = Q.front();Q.pop();
                if (node->left) Q.push(node->left);
                if (node->right) Q.push(node->right);
                sz -= 1;
            }
            ans += 1;
        } 
        return ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

//广度好像是有模板的= =？

（3）101.对称二叉树

给定一个二叉树，检查它是否是镜像对称的。

例如，二叉树 [1,2,2,3,4,4,3] 是对称的。

1
/
2 2
/ \ /
3 4 4 3

但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:

1
/
2 2
\
3 3

官方题解：

1.递归

在这里插入图片描述

class Solution {
public:
    bool check(TreeNode *p, TreeNode *q) {
        if (!p && !q) return true;
        if (!p || !q) return false;
        return p->val == q->val && check(p->left, q->right) && check(p->right, q->left);
    }

    bool isSymmetric(TreeNode* root) {
        return check(root, root);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12

2.迭代

在这里插入图片描述

class Solution {
public:
    bool check(TreeNode *u, TreeNode *v) {
        queue <TreeNode*> q;
        q.push(u); q.push(v);
        while (!q.empty()) {
            u = q.front(); q.pop();
            v = q.front(); q.pop();
            if (!u && !v) continue;
            if ((!u || !v) || (u->val != v->val)) return false;

            q.push(u->left); 
            q.push(v->right);

            q.push(u->right); 
            q.push(v->left);
        }
        return true;
    }

    bool isSymmetric(TreeNode* root) {
        return check(root, root);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

第十二天

（1）226.翻转二叉树

翻转一棵二叉树。

示例：

输入：

4
/
2 7
/ \ /
1 3 6 9
输出：

4
/
7 2
/ \ /
9 6 3 1
备注:
这个问题是受到 Max Howell 的原问题启发的：

谷歌：我们90％的工程师使用您编写的软件(Homebrew)，但是您却无法在面试时在白板上写出翻转二叉树这道题，这太糟糕了。

思路：递归

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void fan(TreeNode* root)
    {
        TreeNode *temp = root->left;
        root->left = root->right;
        root->right = temp;
    }
    void make(TreeNode* root)
    {
        fan(root);
        if(root->left)make(root->left);
        if(root->right)make(root->right);
    }
    TreeNode* invertTree(TreeNode* root) {
        if(root==nullptr)return root;
        //让每一个节点都翻转
        make(root);
        return root;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

官方题解：

1.递归

class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if (root == nullptr) {
            return nullptr;
        }
        TreeNode* left = invertTree(root->left);
        TreeNode* right = invertTree(root->right);
        root->left = right;
        root->right = left;
        return root;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13

（2）112.路经总和

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum ，判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和 targetSum 。

叶子节点是指没有子节点的节点。

示例 1：

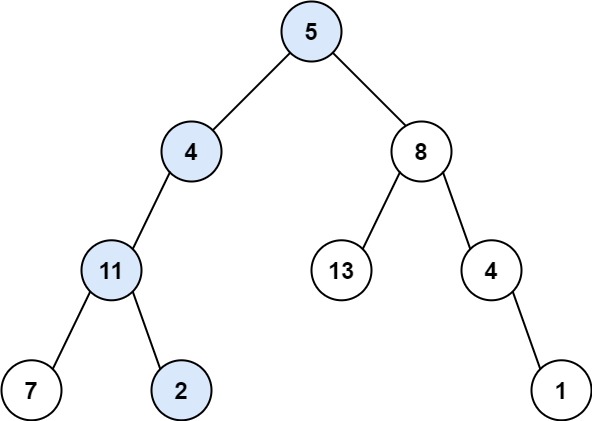
输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true
示例 2：

输入：root = [1,2,3], targetSum = 5
输出：false
示例 3：

输入：root = [1,2], targetSum = 0
输出：false

思路：搜索

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool search(TreeNode *root, int targetSum,int pre)
    { 
        pre+=root->val;
        if(root->left||root->right)
        {
            if(root->left&&search(root->left,targetSum,pre))return true;
            if(root->right&&search(root->right,targetSum,pre))return true;
        }
        else if(targetSum==pre)return true;
        return false;
    }
    bool hasPathSum(TreeNode* root, int targetSum) {
        //深搜
        if(root==nullptr)return false;
        return search(root,targetSum,0);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

官方题解：

1.广度优先搜索

首先我们可以想到使用广度优先搜索的方式，记录从根节点到当前节点的路径和，以防止重复计算。

这样我们使用两个队列，分别存储将要遍历的节点，以及根节点到这些节点的路径和即可。

队列

class Solution {
public:
    bool hasPathSum(TreeNode *root, int sum) {
        if (root == nullptr) {
            return false;
        }
        queue<TreeNode *> que_node;
        queue<int> que_val;
        que_node.push(root);
        que_val.push(root->val);
        while (!que_node.empty()) {
            TreeNode *now = que_node.front();
            int temp = que_val.front();
            que_node.pop();
            que_val.pop();
            if (now->left == nullptr && now->right == nullptr) {
                if (temp == sum) {
                    return true;
                }
                continue;
            }
            if (now->left != nullptr) {
                que_node.push(now->left);
                que_val.push(now->left->val + temp);
            }
            if (now->right != nullptr) {
                que_node.push(now->right);
                que_val.push(now->right->val + temp);
            }
        }
        return false;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

2.递归

思路基本一致，实现不同。
在这里插入图片描述

class Solution {
public:
    bool hasPathSum(TreeNode *root, int sum) {
        if (root == nullptr) {
            return false;
        }
        if (root->left == nullptr && root->right == nullptr) {
            return sum == root->val;
        }
        return hasPathSum(root->left, sum - root->val) ||
               hasPathSum(root->right, sum - root->val);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13

第十三天

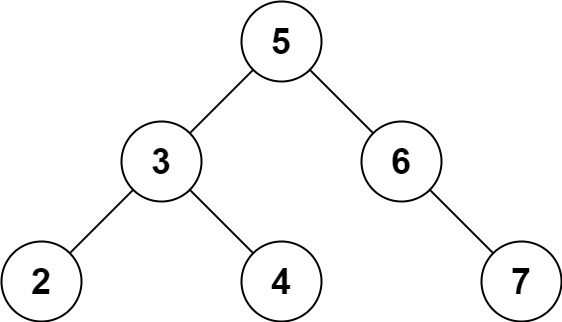
（1）700.二叉搜索树中的搜索

给定二叉搜索树（BST）的根节点和一个值。你需要在BST中找到节点值等于给定值的节点。返回以该节点为根的子树。如果节点不存在，则返回 NULL。

例如，

给定二叉搜索树:
 4
 / \
1
2
2 7
/
1 3

和值: 2
你应该返回如下子树:

2
/ \
1 3
在上述示例中，如果要找的值是 5，但因为没有节点值为 5，我们应该返回 NULL。

思路：搜索然后返回，可以利用二叉搜索树的性质简化

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        if(root->val==val)return root;
        if(root->left){
            TreeNode *temp = searchBST(root->left,val);
            if(temp!=NULL)return temp;
        }
        if(root->right){
            TreeNode *temp = searchBST(root->right,val);
            if(temp!=NULL)return temp;
        }
        return NULL;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

二叉搜索树

二叉查找树（Binary Search Tree），（又：二叉搜索树，二叉排序树）它或者是一棵空树，或者是具有下列性质的二叉树：若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；它的左、右子树也分别为二叉排序树。二叉搜索树作为一种经典的数据结构，它既有链表的快速插入与删除操作的特点，又有数组快速查找的优势；所以应用十分广泛，例如在文件系统和数据库系统一般会采用这种数据结构进行高效率的排序与检索操作。

改进后：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        if(root->val==val)return root;
        if(val<root->val&&root->left){
            TreeNode *temp = searchBST(root->left,val);
            if(temp!=NULL)return temp;
        }
        if(val>root->val&&root->right){
            TreeNode *temp = searchBST(root->right,val);
            if(temp!=NULL)return temp;
        }
        return NULL;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

官方题解：

1.递归

同爷的思路

2.迭代

在这里插入图片描述

class Solution:
    def searchBST(self, root: TreeNode, val: int) -> TreeNode:
        while root is not None and root.val != val:
            root = root.left if val < root.val else root.right
        return root
1
2
3
4
5

（2）701.二叉搜索树中的插入操作

给定二叉搜索树（BST）的根节点和要插入树中的值，将值插入二叉搜索树。返回插入后二叉搜索树的根节点。输入数据保证，新值和原始二叉搜索树中的任意节点值都不同。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。你可以返回任意有效的结果。

示例 1：

输入：root = [4,2,7,1,3], val = 5
输出：[4,2,7,1,3,5]
解释：另一个满足题目要求可以通过的树是：

示例 2：

输入：root = [40,20,60,10,30,50,70], val = 25
输出：[40,20,60,10,30,50,70,null,null,25]
示例 3：

输入：root = [4,2,7,1,3,null,null,null,null,null,null], val = 5
输出：[4,2,7,1,3,5]

思路：找到合适的空指针，插入

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void insert(TreeNode* root,int val)
    {
        int a = root->val;
        if(val>a)
        {
            if(root->right==nullptr)
            {
                TreeNode *temp = new TreeNode(val);
                root->right = temp;
            }
            else insert(root->right,val);
        }
        else
        {
            if(root->left==nullptr)
            {
                TreeNode* temp = new TreeNode(val);
                root->left = temp;
            }
            else insert(root->left,val);
        }
    }
    TreeNode* insertIntoBST(TreeNode* root, int val) {
        //小在左大在右
        if(root)insert(root,val);
        else root = new TreeNode(val);
        return root;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

官方题解：

1.模拟

同我的思路，代码有优化，没有递归

class Solution {
public:
    TreeNode* insertIntoBST(TreeNode* root, int val) {
        if (root == nullptr) {
            return new TreeNode(val);
        }
        TreeNode* pos = root;
        while (pos != nullptr) {
            if (val < pos->val) {
                if (pos->left == nullptr) {
                    pos->left = new TreeNode(val);
                    break;
                } else {
                    pos = pos->left;
                }
            } else {
                if (pos->right == nullptr) {
                    pos->right = new TreeNode(val);
                    break;
                } else {
                    pos = pos->right;
                }
            }
        }
        return root;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

第十四天

（1）98.验证二叉搜索树

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效二叉搜索树定义如下：

节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

输入：root = [2,1,3]
输出：true
示例 2：

输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

思路：按定义去慢慢验证

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool checkbig(TreeNode* root,int x)
    {
        //左面都比中间小
        if(root==nullptr)return true;
        bool flag = true;
        if(root->val>=x)return false;
        if(root->left)flag = checkbig(root->left,x);
        if(!flag)return false;
        if(root->right)flag = checkbig(root->right,x);
       // cout << 'l' << flag << endl;
        return flag;
    }
    bool checksmall(TreeNode* root,int x)
    {
        if(root==nullptr)return true;
        bool flag = true;
        if(root->val<=x)return false;
        if(root->left)flag = checksmall(root->left,x);
        if(!flag)return false;
        if(root->right)flag = checksmall(root->right,x);
        return flag;  
    }
    bool check(TreeNode* root)
    { 
        if(root!=nullptr)
        {
            bool flag = true;
            int a = root->val;
            if(root->left)
            {            
                flag = checkbig(root->left,a);
                //cout << 'l' << flag << endl;
                if(!flag)return false;
                int b = root->left->val;
                if(b>=a)return false;
                else flag = check(root->left);
            }
            if(!flag)return false;
            if(root->right)
            {
                flag = checksmall(root->right,a);
              //  cout << 'r' << endl;
                if(!flag)return false;
                int b = root->right->val;
                if(b<=a)return false;
                else flag = check(root->right);
            }
            return flag;
        }
        else return true;
        
    }
    bool isValidBST(TreeNode* root) {
        return check(root);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69

官方题解：

1.递归

在这里插入图片描述

class Solution {
public:
    bool helper(TreeNode* root, long long lower, long long upper) {
        if (root == nullptr) {
            return true;
        }
        if (root -> val <= lower || root -> val >= upper) {
            return false;
        }
        return helper(root -> left, lower, root -> val) && helper(root -> right, root -> val, upper);
    }
    bool isValidBST(TreeNode* root) {
        return helper(root, LONG_MIN, LONG_MAX);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

2.中序遍历

在这里插入图片描述
fig1

class Solution {
public:
    bool isValidBST(TreeNode* root) {
        stack<TreeNode*> stack;
        long long inorder = (long long)INT_MIN - 1;

        while (!stack.empty() || root != nullptr) {
            while (root != nullptr) {
                stack.push(root);
                root = root -> left;
            }
            root = stack.top();
            stack.pop();
            // 如果中序遍历得到的节点的值小于等于前一个 inorder，说明不是二叉搜索树
            if (root -> val <= inorder) {
                return false;
            }
            inorder = root -> val;
            root = root -> right;
        }
        return true;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

（2）653.两数之和IV-输入BST

给定一个二叉搜索树 root 和一个目标结果 k，如果 BST 中存在两个元素且它们的和等于给定的目标结果，则返回 true。

示例 1：

输入: root = [5,3,6,2,4,null,7], k = 9
输出: true
示例 2：

输入: root = [5,3,6,2,4,null,7], k = 28
输出: false
示例 3：

输入: root = [2,1,3], k = 4
输出: true
示例 4：

输入: root = [2,1,3], k = 1
输出: false
示例 5：

输入: root = [2,1,3], k = 3
输出: true

思路：无，所以强改成数组做了【

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void getnums(TreeNode* root,vector<int>& nums)
    {
        if(root){
        nums.push_back(root->val);
        if(root->right)getnums(root->right,nums);
        if(root->left)getnums(root->left,nums);
        }  
    }
    bool findTarget(TreeNode* root, int k) {
        //不知道怎么利用二叉搜索树的性质，所以当数组做了
        vector<int> nums;
        getnums(root,nums);
        for(int i=0;i<nums.size();i++)
            for(int j=i+1;j<nums.size();j++)
            if(nums[i]+nums[j]==k)return true;
        return false;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

官方题解：

1.使用 HashSet【通过】

在这里插入图片描述
【只有java

public class Solution {
    public boolean findTarget(TreeNode root, int k) {
        Set < Integer > set = new HashSet();
        return find(root, k, set);
    }
    public boolean find(TreeNode root, int k, Set < Integer > set) {
        if (root == null)
            return false;
        if (set.contains(k - root.val))
            return true;
        set.add(root.val);
        return find(root.left, k, set) || find(root.right, k, set);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

2.使用 BFS 和 HashSet【通过】

在这里插入图片描述

public class Solution {
    public boolean findTarget(TreeNode root, int k) {
        Set < Integer > set = new HashSet();
        Queue < TreeNode > queue = new LinkedList();
        queue.add(root);
        while (!queue.isEmpty()) {
            if (queue.peek() != null) {
                TreeNode node = queue.remove();
                if (set.contains(k - node.val))
                    return true;
                set.add(node.val);
                queue.add(node.right);
                queue.add(node.left);
            } else
                queue.remove();
        }
        return false;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

3.使用 BST【通过】

在这里插入图片描述

public class Solution {
    public boolean findTarget(TreeNode root, int k) {
        List < Integer > list = new ArrayList();
        inorder(root, list);
        int l = 0, r = list.size() - 1;
        while (l < r) {
            int sum = list.get(l) + list.get(r);
            if (sum == k)
                return true;
            if (sum < k)
                l++;
            else
                r--;
        }
        return false;
    }
    public void inorder(TreeNode root, List < Integer > list) {
        if (root == null)
            return;
        inorder(root.left, list);
        list.add(root.val);
        inorder(root.right, list);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

（3）235.二叉搜索树的最近公共祖先

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

示例 1:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

说明:

所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉搜索树中。

思路：无，真的不知道怎么找祖先

官方题解：

1.两次遍历

在这里插入图片描述
重点找最后一个相同点

class Solution {
public:
    vector<TreeNode*> getPath(TreeNode* root, TreeNode* target) {
        vector<TreeNode*> path;
        TreeNode* node = root;
        while (node != target) {
            path.push_back(node);
            if (target->val < node->val) {
                node = node->left;
            }
            else {
                node = node->right;
            }
        }
        path.push_back(node);
        return path;
    }

    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        vector<TreeNode*> path_p = getPath(root, p);
        vector<TreeNode*> path_q = getPath(root, q);
        TreeNode* ancestor;
        for (int i = 0; i < path_p.size() && i < path_q.size(); ++i) {
            if (path_p[i] == path_q[i]) {
                ancestor = path_p[i];
            }
            else {
                break;
            }
        }
        return ancestor;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

2.一次遍历

在这里插入图片描述

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        TreeNode* ancestor = root;
        while (true) {
            if (p->val < ancestor->val && q->val < ancestor->val) {
                ancestor = ancestor->left;
            }
            else if (p->val > ancestor->val && q->val > ancestor->val) {
                ancestor = ancestor->right;
            }
            else {
                break;
            }
        }
        return ancestor;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

写完了也开学了，希望能管点用吧【祈祷ing】

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/从前慢现在也慢/article/detail/788801