Delaunay三角剖分算法_delaunay 三角剖分算法

一. 简介

点集的三角剖分（Triangulation），对数值分析（比如有限元分析）以及图形学来说，都是极为重要的一项预处理技术。尤其是Delaunay三角剖分，由于其独特性，关于点集的很多种几何图都和Delaunay三角剖分相关，如Voronoi图，EMST树，Gabriel图等。Delaunay三角剖分有最大化最小角，最接近于规则化的三角网和唯一性（任意四点不能共圆）两个特性。

Delaunay三角剖分广泛应用于许多不同应用程序中的科学计算。虽然有大量的计算三角剖分的算法，但Delaunay三角剖分以其实用的几何属性广受欢迎。

1.1 三角剖分

三角剖分就是对给定的平面点集，生成三角形集合的过程。考虑平面点集P={P1，…，Pn}，我们希望得到三角形集合T=在{t1，…，tm}，满足：

• 所有三角形的端点恰好构成集合P；
• 任意两个三角形的边不相交（要么重合，要么没有交点）；
• 平面图中所有的面都是三角面，且所有三角形的合集构成P的凸包（convex hull）。

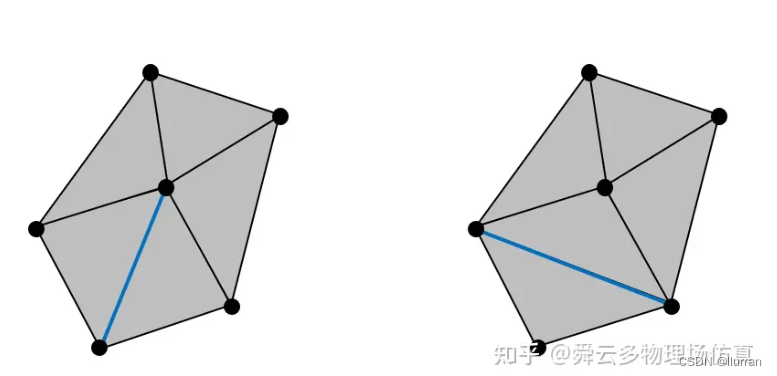
一般来说，给定一个点集，往往存在不止一个三角剖分。以下图为例，我们只要把第一个三角剖分中的两个相邻三角形的公共边做一次翻转，就可以得到一个新的三角剖分。

由于给定点集的三角剖分不唯一，我们希望从中挑选出一个“最优”的三角剖分。那么何为最优？这涉及到三角形“质量”的评定。一般在数值计算中，我们不希望三角形过于狭长，也就是说越接近等边三角形越好。以下是几种常见的质量评定标准：

• 最小角（minimum angle）：即所有三角形的内角当中最小的角；
• 纵横比（aspect ratio）：三角形最短边与最长边的比例；
• 半径比（radius ratio）：三角形内接圆半径的两倍与外接圆半径的比例。

1.2 Delaunay三角剖分

所有三角形的外接圆均满足空圆性质的三角剖分，称为一个Delaunay三角剖分。

1. 空圆性质
   Delaunay三角网是唯一的（任意四点不能共圆），在Delaunay三角网中任一三角形（或边）的外接圆范围内（边界除外）不会有其他点存在。
   
   

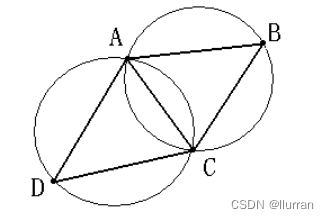
左图的三角剖分是Delaunay的，任何一个三角形的外接圆内部都不包含点集中的顶点；
右图的三角剖分不是Delaunay的，因为下面的两个三角形的外接圆内部包含了顶点。

二. Delaunay三角剖分的相关理论

2.1 Delaunay三角形和（局部）Delaunay边的概念

• 对三角剖分中的一个三角形，如果其外接圆满足空圆性质，称为一个Delaunay三角形；
• 对三角剖分中的一条边，若存在一个外接圆满足空圆性质，称为一条Delaunay边（一条边的外接圆可以是经过这条边两个顶点的任意圆，不唯一）；
• 对三角剖分中的一条属于两个三角形t1，t2的边e，若存在一个外接圆不包含三角形t1，t2中的任何顶点称为局部Delaunay边。若一条边只属于一个三角形，也属于局部Delaunay边。

2.2 Delaunay引理

对一个三角剖分T，以下三个命题互相等价：

• T中所有三角形均为Delaunay三角形；
• T中所有三角形的边均为Delaunay边；
• T中所有三角形的边均为局部Delaunay边。

2.3 翻转边算法（flip algorithm）

定理：对三角剖分T中的一条边e，若它不是局部Delaunay的，则可以被翻转成为一条局部Delaunay边e’。

边的翻转：假设一条边e属于两个三角形t1，t2，这两个三角形的合集所构成的四边形有两条对角线，e为其中一条。现在用另一条对角线e’替换e，得到两个新的三角形t1’，t2’，并用这两个新的三角形替换原三角剖分中的t1，t2，得到新的三角剖分T’。这个操作称为边的翻转。

每进行一次翻转边操作时，都把三角剖分“局部”地改善了。更具体的讲，有以下结论：

• 最小角增大：翻转边e后的两个相邻三角形的6个内角中的最小角大于等于原先的两个三角形6个内角中的最小角；
• 外接圆半径缩小：翻转边e后的两个相邻三角形的外接圆半径最大值小于原先的两个三角形外接圆半径的最大值；
• 四点共圆的情况：若一条边e的两个相邻三角形的顶点A，B，C，D四点共圆，则无论翻转与否，这条边都是局部Delaunay边。

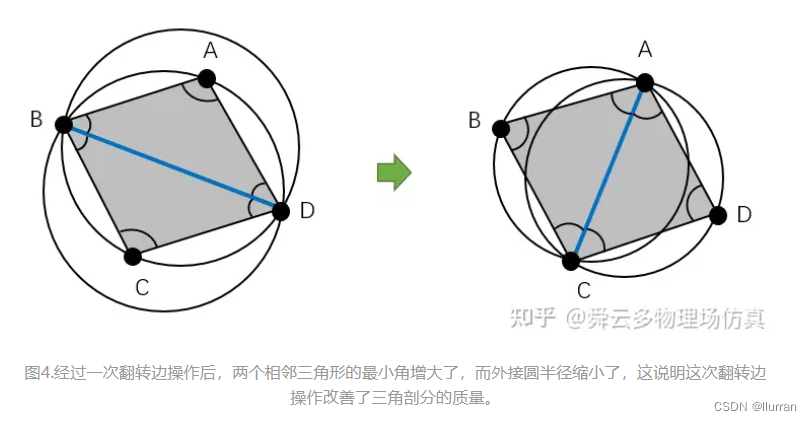
根据Delaunay引理，对任意一个三角剖分T，只要持续进行上述的翻转边操作，最终总可以转化为一个Delaunay三角剖分。

2.4 Delaunay三角剖分的最优性质

1. 最大化最小角性质：
   在给定点集P的所有三角剖分中，Delaunay三角剖分得到的最小角是最大的。
2. 最小化外接圆性质：
   在给定点集P的所有三角剖分中，Delaunay三角剖分得到的最大外接圆半径是最小的。
3. 若点集P中任意四点不共圆，则存在唯一的Delaunay三角剖分T。若点集P中四点A,B,C,D共圆，且△ABC,△BCD属于Delaunay三角剖分T，那么将边BC翻转后得到的三角剖分T’(包含△ABD,△ACD)同样是一个Delaunay三角剖分。

三. Delaunay三角剖分的构造算法

3.1 Lawson算法

1. 先计算点集P的包围盒（bounding box），将包围盒的四个顶点加入P中得到P’。根据包围盒生成两个超三角形（super triangles），构成初始三角剖分T0。由于只包含两个直角三角形，T0是（包围盒四个顶点的）一个Delaunay三角剖分。
2. 将点集P中的顶点逐一插入现有的三角剖分Ti中，并进行如下调整：

• 设插入的顶点v位于三角形t中，将v与三角形的三个顶点连接，使t分裂为3个三角形t1，t2，t3；
• 分别检查t1，t2，t3是否满足空圆性质，若不满足则进行翻转边操作，直到没有坏边为止。此时得到一个包含顶点v的新Delaunay三角剖分。

3. 当最后一个顶点插入到三角剖分中，并且完成所有翻转边操作后，我们得到了点集P’的一个Delaunay三角剖分。现在删除第一步中加入的包围盒的四个顶点，并且去除所有与它们连接的三角形，则剩下的三角形就构成点集P的Delaunay三角剖分T。

3.2 Bowyer-Watson算法

1. 同Lawson算法
2. 将点集P中的顶点逐一插入现有的三角剖分中，并进行如下调整：

• 在现有三角剖分中，所有外接圆包含顶点v的三角形的合集构成一个“星形多边形”。星形多边形的含义是多边形的任何一个顶点到v的连线都在多边形内部。
• 对于上述星形多边形，将其内部的三角形全部删除，形成一个“空穴”。将空穴边界的顶点与新添加的顶点v连接得到新的三角形，替代剖分中被删除的三角形，此时得到一个包含顶点v的新Delaunay三角剖分。

3. 同Lawson算法

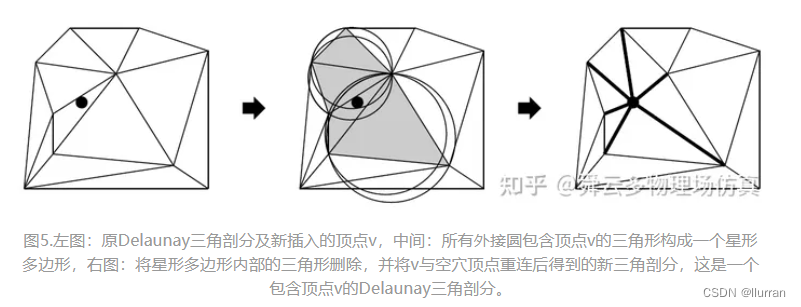
由于Delaunay三角剖分的唯一性，两种算法在效果上没什么区别。但Bowyer-Watson算法因为缩短了搜索坏边的过程，效率会更高一些，所以实际应用中我们往往使用Bowyer-Watson算法。

四. 基于Delaunay三角剖分法的网格生成算法

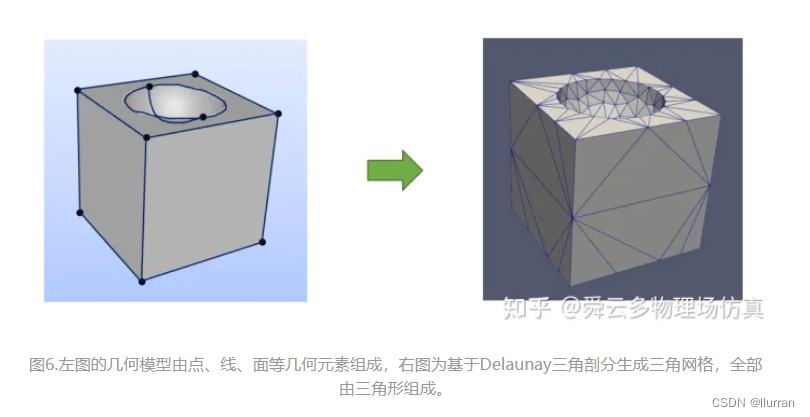
4.1 Delaunay平面区域网格生成算法

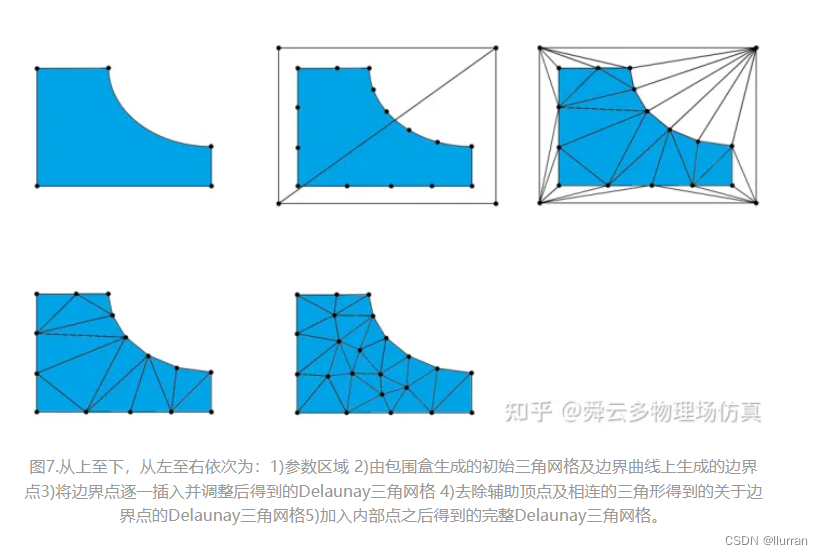
生成三角网格与构造三角剖分的主要区别在于，点集P并非给定，需要自己去生成。而一旦确定了点集P，剩下的工作就是构造三角剖分了。实际上，生成点集P与构造三角剖分的过程是同时进行的，其过程如下：

• 计算区域的包围盒，生成两个超三角形作为初始三角网格，根据边界曲线生成边界点；
• 将边界点逐一插入到三角网格中，每一步插入后，用Bowyer-Watson算法得到新的Delaunay三角网格；
• 将第一步插入的辅助顶点删除（同时删除与其连接的三角形），得到关于全部边界点的Delaunay三角网格（亦即边界点的Delaunay三角剖分）；
• 在区域内部的三角形，根据一定的条件，将重心插入三角网格，并根据Bowyer-Watson算法调整，得到新的Delaunay三角剖分。直到不再有需要插入的重心点，此时得到区域的完整Delaunay三角网格。

4.2 三维模型的Delaunay三角网格生成算法

1. 遍历模型的所有边（edge），生成边界点；
2. 遍历模型的所有面（face），收集其边界点在参数区域的坐标。然后在参数区域上按照上面的算法生成Delaunay三角网格；
3. 将每个面在参数区域上生成的内部点和三角形投射到三维空间，添加到三角网格中；

这里要注意的是，每个面上的点需要两份编号，一个局部（local）编号用于参数区域上的三角网格，及一个全局（global）编号用于三维空间的整体三角网格。在网格生成过程中需要时刻保持这两种编号的对应关系。

参考文章：
https://zhuanlan.zhihu.com/p/459884570
https://ww2.mathworks.cn/help/matlab/math/delaunay-triangulation.html
https://blog.csdn.net/qq_43258953/article/details/105080150