MoE 系列论文解读：Gshard、FastMoE、Tutel、MegaBlocks 等

节前，我们组织了一场算法岗技术&面试讨论会，邀请了一些互联网大厂朋友、今年参加社招和校招面试的同学。

针对大模型技术趋势、大模型落地项目经验分享、新手如何入门算法岗、该如何准备面试攻略、面试常考点等热门话题进行了深入的讨论。

总结链接如下：《AIGC 面试宝典》(2024版) 正式发布！

---

这篇文章中，我们简单回顾一下 MoE 的发展历程，介绍几个有代表性的 MoE 模型（按照时间顺序）。

1.1 马斯克发布 314B Grok-1

最近马斯克开源了 Twitter（xAI）的 LLM Grok-1，其包含 314B 参数量，是当前最大的开源 LLM，其对应的配置如下图所示（对应的代码库为 https://github.com/xai-org/grok-1/tree/main），可以看出：

• 词表大小为 128*1024=131072

• 序列长度为 8192

• Embedding 大小为 6144

• 使用了 GQA（每 6 个一组），8 个 KV Head，48 个 Query Head

• 总共 64 层

• 采用了 MoE，每层 8 个专家，每次激活 2 个专家

1.2 数据、模型、专家并行

随着模型规模的增加，往往需要结合各种分布式并行策略，以下是 3 种并行策略及其相互融合（来自论文 [2101.03961] Switch Transformers: Scaling to Trillion Parameter Models with Simple and Efficient Sparsity），包括数据并行（Data Parallel，DP）、模型并行（Model Parallel，MP，或者称为 Tensor Parallel，TP）和专家并行（Expert Parallel，EP）；实际上还有常见的流水线并行（Pipeline Parallel，PP）；此外通过将大的 Batch 拆分为小的 Micro Batch 进行梯度累加，不同 Micro Batch 之间可以通过 Overlap 方式减少 Bubble，也是常用的方案，以上两种这里不再展开（需要说明的是，这里不包含 ZeRO 系列的并行策略，比如 ZeRO-DP 实际上也会切分模型参数）：

如下图所示，从模型参数切分和数据切分的角度考虑（只考虑 FFN 层）：

• 第一列：数据并行

• 上：所有设备（1-16）都有相同、全部的模型参数。

• 下：每个设备只有一个数据分片，且不重复，共 16 个数据分片。

• 第二列：模型并行

• 上：所有设备（1-16）都只有模型参数的一部分，共 16 个分片。

• 下：所有设备使用共同的一份数据。

• 第三列：模型并行+数据并行，设备分为 4 组（1-4,5-8,9-12,13-16）

• 上：每组（4 个设备）都有完整的模型参数副本，但是每组内的设备只有参数的一部分。

• 下：数据分为 4 个切片，每组（4 个设备）对应一个数据切片。

• 第四列：专家并行+数据并行，设备分为 16 组（1-16）

• 上：每一个设备都有不同的专家，共 16 个专家。

• 下：每个设备都有不同的数据分片（Token），共 16 个数据分片，一个专家对应一个分片。

• 第五列：专家并行+模型并行+数据并行，有 4 组设备（1-4,5-8,9-12,13-16）

• 上：有 4 个专家，每个专家分布在对应的 4 个设备上，比如绿色专家分布在 5,6,7,8 设备上。

• 下：有 4 个数据分片，每组设备（每个专家）对应一个数据分片，一组设备里的 4 个设备共享一份数据分片。

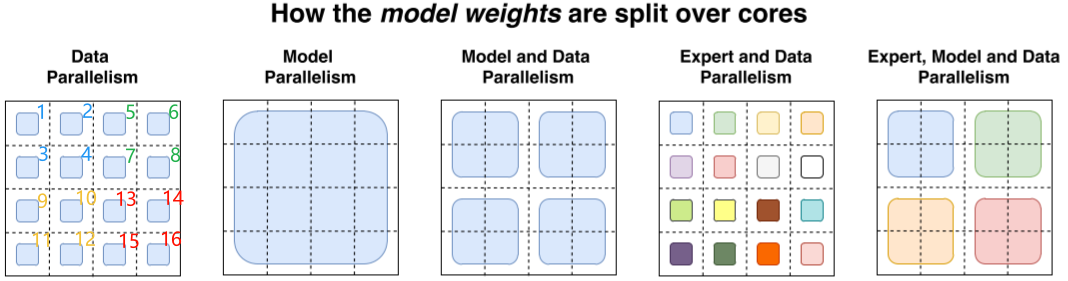
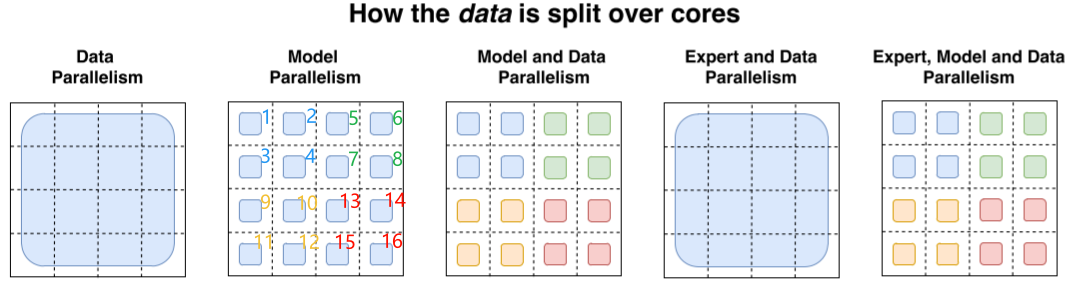
1.3 补充

在了解这些文章时，需要考虑每个系统的潜在假设以及针对的场景，比如：

1. 专家数量和 GPU（TPU）数量的关系可能导致不同的分布式并行策略：

• 早期模型中每层的专家数非常多，可能达到几百甚至几千，此时通常是一个 GPU 一个专家（Gshard）或者一个 GPU 上多个专家。

• 最近的 LLM-MoE 中，专家数量往往很小，可能只有 8 个或 16 个，而训练 LLM 的 GPU 往往达到几百、几千甚至上万个，往往可以将一个专家放在多个 GPU 上。此时也需要考虑切分方式，比如平均 1 个专家对应 4 个 GPU：

• 一种方案是：2 个专家共享 8 个 GPU，每个 GPU 有 2 个专家的各 1/8

• 另一种方案是：1 个专家独享 4 个 GPU，每个 GPU 有 1 个专家的 1/4

2. 模型中除了 MoE 之外还包含多个模块，比如 Transformer 模型除了 FFN 还有 Attention，而很多工作都重点考虑 MoE（FFN）的专家模块。在 Attention 模块除了 DP 之外也可以使用 MP（TP）。

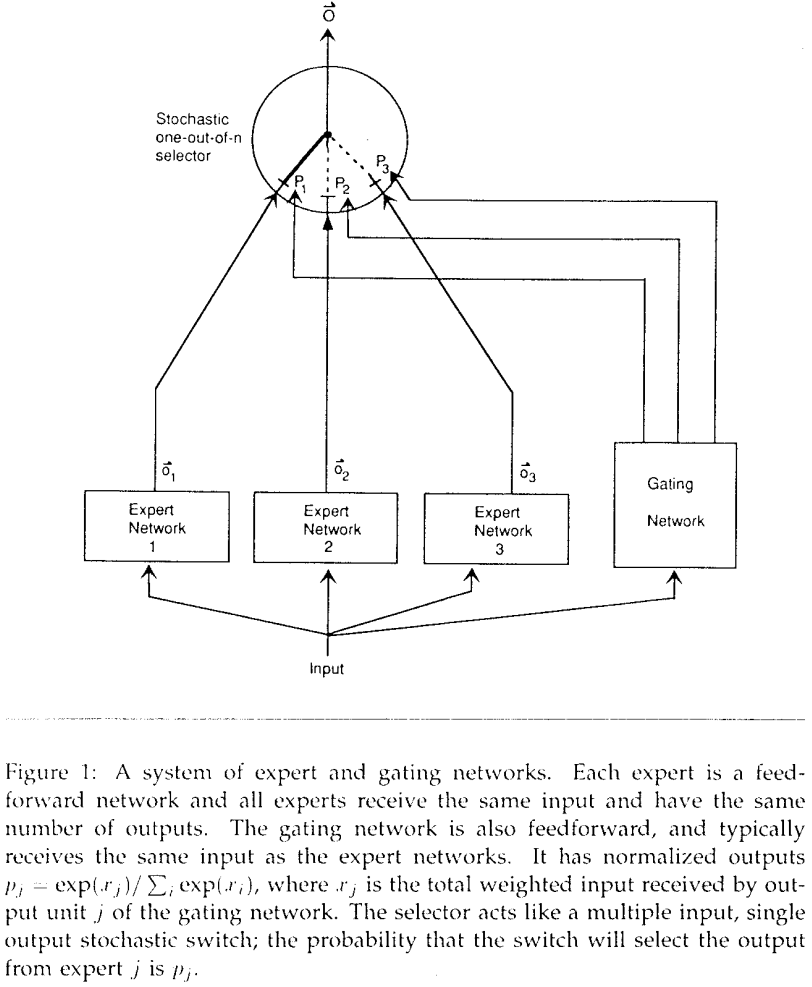
二、Adaptive Mixture of Local Experts

MoE 的概念起源自 1991 年的 Paper Adaptive Mixtures of Local Experts，其中每个 Expert Network 和 Gating Network 都会接受 Input，并执行各自的部分，Gating Network 会学习到各个 Expert 的权重，并将输出按照权重进行归一化，如下图所示：

三、Sparsely-Gated MoE

在 [1701.06538] Outrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer 中，作者（也包括大名鼎鼎的 Geoffrey Hinton 和 Jeff Dean）将 MoE 引入到 LSTM 模型中，并提出了稀疏 MoE（Sparse MoE）的概念。

如下图 Figure 1 所示，作者引入了 Gating Network 机制，该机制可以选出 Topk 的 Expert（深灰色 Expert 2 和 Expert n-1）进行计算。这种稀疏性意味着只有部分专家被激活处理特定的输入，从而可以大大降低计算量：

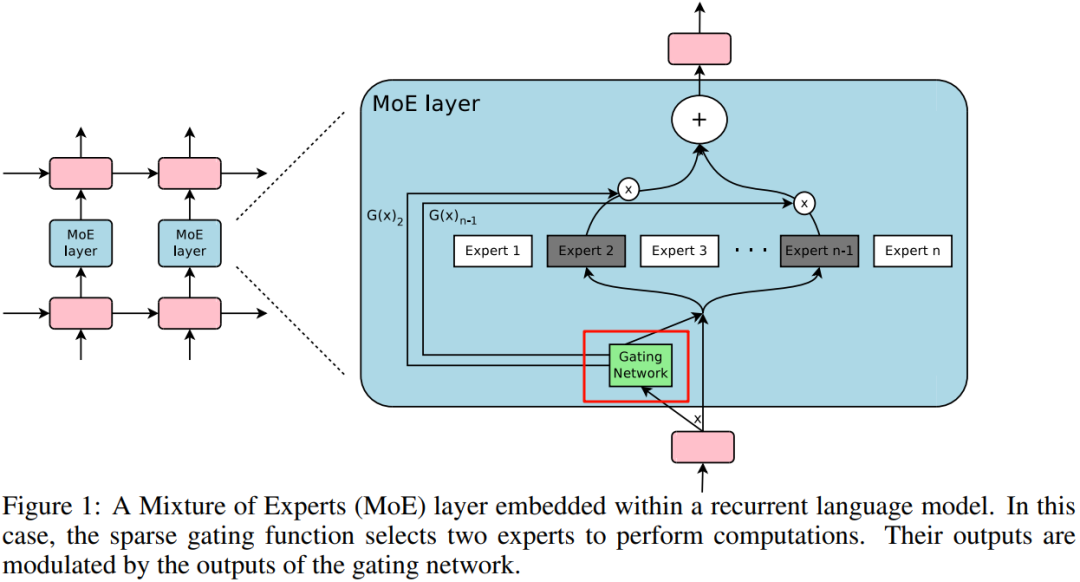
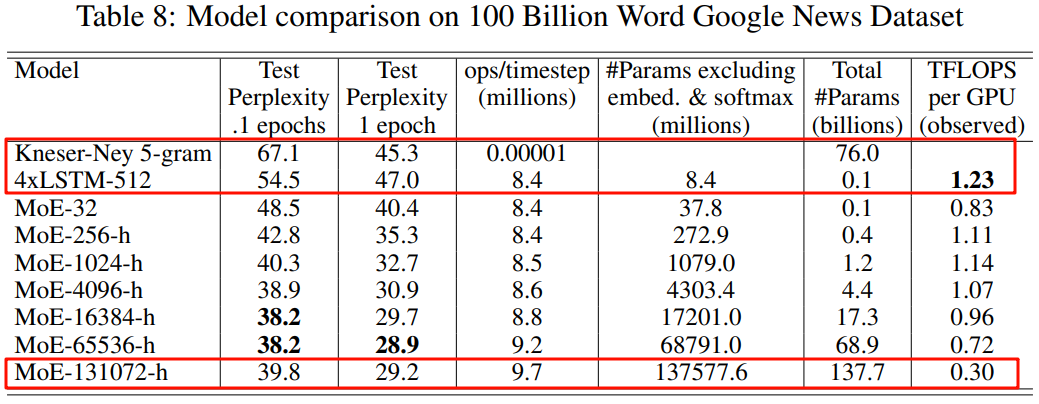
作者也进一步证明通过添加 MoE，可以灵活控制专家数，来获得不同容量的模型。如下图 Table 8 所示，作者分别构建了 32/256/1024/4096/16384/65535/131072 个专家的模型，其最大的为 137B 的 LSTM 模型。由于稀疏性的存在，虽然 137B 参数量很大，但可以比当时 SOTA 模型更低的计算成本下获得更好的效果：

作者观察到，Gating Network 倾向于收敛到不均衡的状态，也就是总是为少数专家产生较大的权重（相应的参数更新也会很不均衡）。为了解决这一问题，作者设计了额外的损失函数，旨在鼓励所有专家具有同等的重要性，如下图所示：

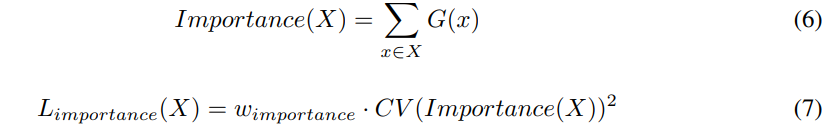
四、Gshard

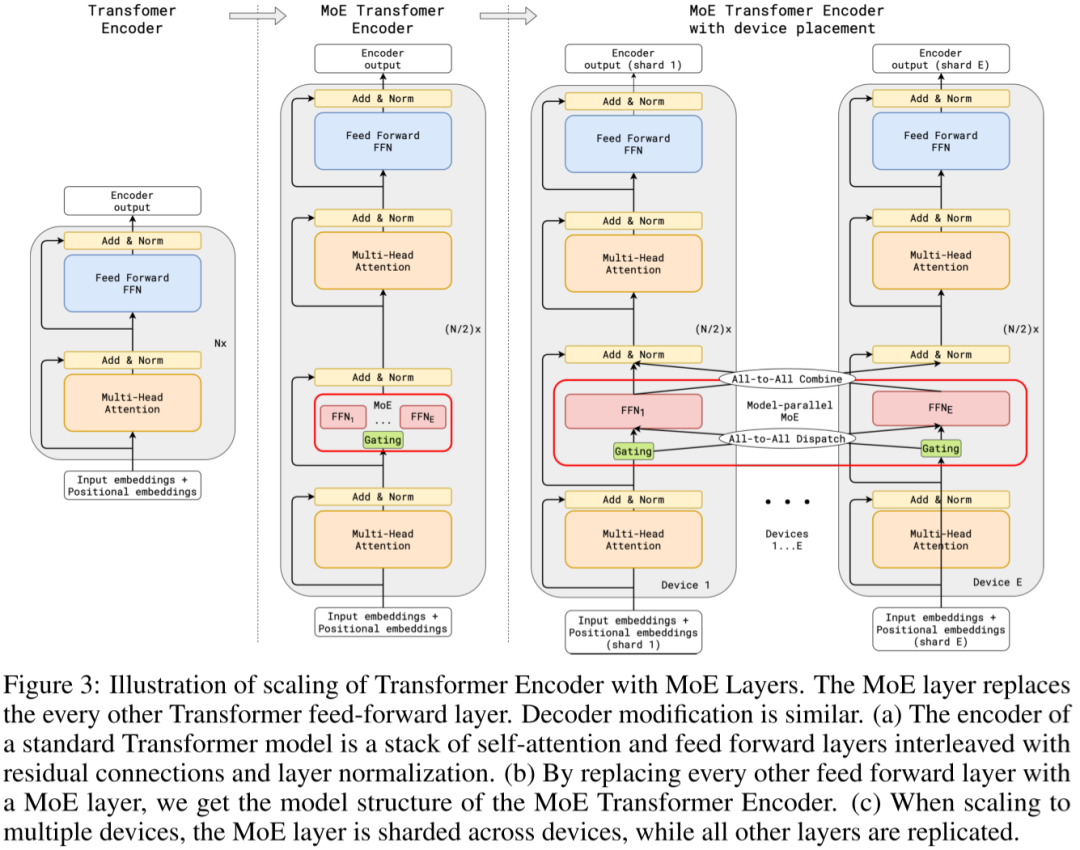
在 [2006.16668] GShard: Scaling Giant Models with Conditional Computation and Automatic Sharding 中，作者首次将 MoE 引入到 Transformer 模型中。如下图 Figure 3 所示：

• 增加 Position-wise Sparsely Gated MoE 层，将 FFN 层替换为 MoE 结构，MoE 中的每个专家都是一个 FFN（每个专家大小相同）

• Gating 模块：通过 Gating 模块将输入路由到不同的专家（Transformer 模型输入的是 Token 序列，因此每个 Token 都会通过 Gating 选择不同的专家，而不是整个序列使用相同的专家，默认为 top2）。

• Random routing：有些时候 Gating 模块得到的排名第二的专家的分数会很低，此时可以简单地忽略第二个专家。

• 并非是每一层的 FFN 都替换为 MoE，而是间隔一层替换，如果有 12 层，则只有 6 层有 MoE（通常是可配置的）。

• 采用专家并行（Expert Parallel，EP）策略，每个设备一个专家，除 MoE 之外的模型其它部分在所有设备存储一份相同的副本。（如果有 128 个专家，则使用 128 个 TPU Core；2048 个专家，则使用 2048 个 TPU Core）

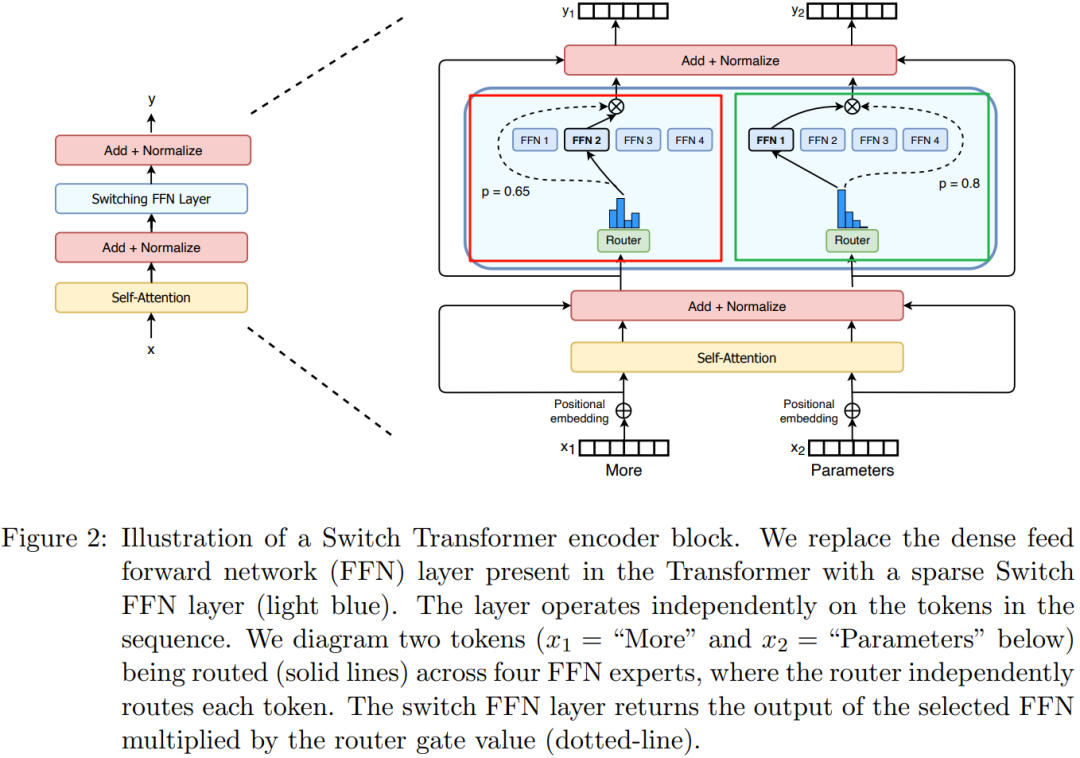
五、Switch Transformer

在 [2101.03961] Switch Transformers: Scaling to Trillion Parameter Models with Simple and Efficient Sparsity 中，作者相比 Gshard 等方案主要做了三点改进。

5.1 简化稀疏路由

在 [1701.06538] Outrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer 中，作者认为选择的稀疏专家的数目需要 > 1，在 Gshard 中作者也是使用的 top2 专家。而 Switch Transformer 中，作者发现仅使用一个专家也能保证模型的质量。这样有 3 个好处：

• Router 计算更简单，通信量也更少。

• 一个 Token 仅对应一个专家，计算量也更少。

• 平均每个专家对应的 batch size 至少可以减半。

如下图 Figure 2 所示，其模型结构和 Gshard 中类似，图中的红框和绿框是同样的 MoE，只是对应不同的输入，经 Router 后也只连接一个专家：

5.2 高效稀疏路由

作者采用了 Mesh-TensorFlow，其提供和 TensorFlow 相似的 API，提供了更简单的分布式数据并行和模型并行。作者的模型主要针对 TPU 设计，其在模型训练中不支持动态 Tensor shape，也就是要求每个专家输入的 Tensor shape 是固定的。然而，路由是动态的，相应路由到每个专家的 Tensor 的 shape 也是动态的，为了解决这一问题，作者提出了专家容量（Expert Capacity）的概念。如下所示，专家容量为每个 Batch 中总的 Token 数除以专家数，然后再乘以容量因子（Capacity Factor），即可得到专家容量（每个专家对应的 Token 数）。

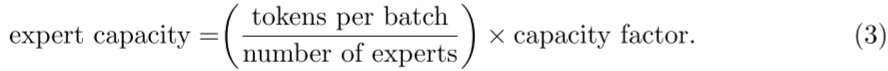
如下图 Figure 3 所示，有 6 个 Token，3 个专家，平均每个专家 2 个 Token：

• 容量因子为 1.0：如下图中所示，则对应的专家容量为 2：

• Expert 1 有 3 个 Token，则需要丢弃一个通过残差连接直接传到下一层。

• Expert 2 有 2 个 Token，正好。

• Expert 3 只有 1 个 Token，需要 Padding 1 个空的 Token。

• 容量因子为 1.5：如下图右所示，则对应的专家容量为 3：

• Expert 1 有 3 个 Token，正好。

• Expert 2 只有 2 个 Token，需要 Padding 1 个空的 Token。

• Expert 3 只有 1 个 Token，需要 Padding 2 个空的 Token。

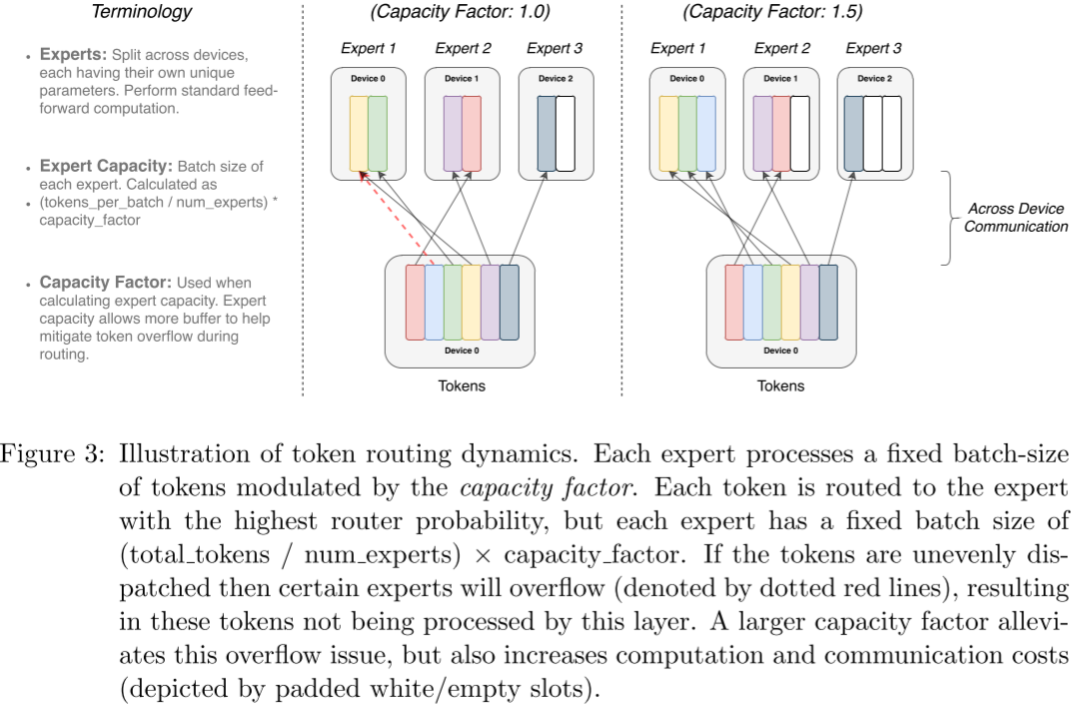
从上也可以看出，容量因子越大，需要 Padding 的 Token 也就越多，无效计算越多；负载越不均衡，需要 Padding 的 Token 也就越多，无效计算越多。为了更好地实现负载均衡，作者同样添加了 Load Balancing Loss。

5.3 增强的训练和微调技巧

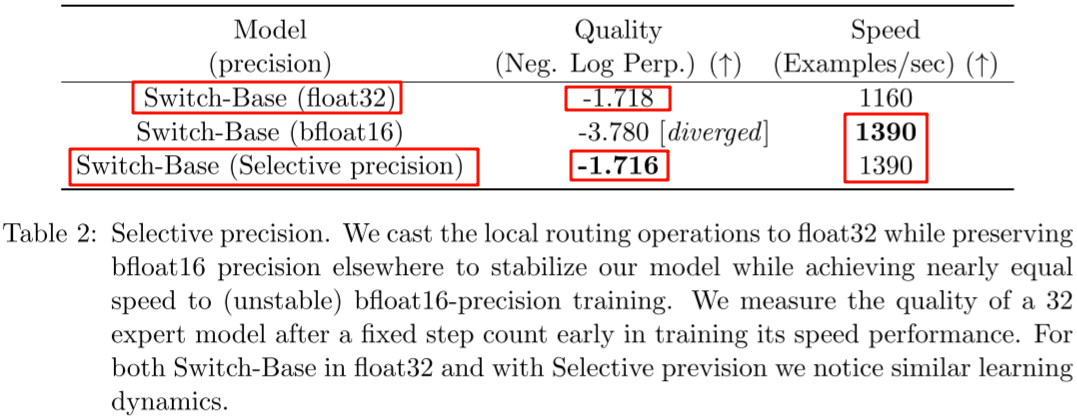
Selective precision：稀疏专家模型相比传统 Transformer 模型训练更加困难，由于每一层 Router 的存在，可能导致训练的不稳定性，此外 BF16 等低精度格式可能加剧 Router 中 Softmax 计算的问题。本文作者提出了在模型的局部部分选择性地转为 FP32 精度，可以实现很好的稳定性，而不会产生昂贵的 FP32 Tensor 通信成本。具体来说，只在 Router 的内部使用 FP32 精度。如下图 Table 2 所示，本文的 Selective precision 可以同时实现高质量和高吞吐：

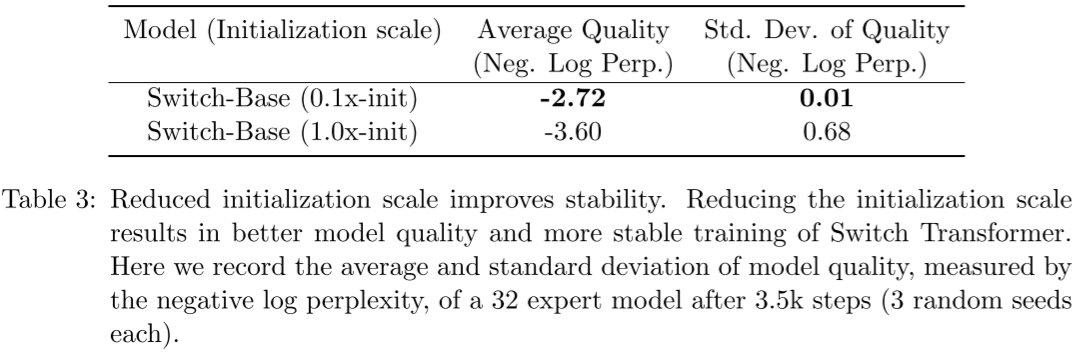
小的初始化参数有助于稳定性：如下图所示，作者验证通过使用比较小的初始化参数可以获得更好的模型质量，并减小模型在训练早期的方差：

Dropout 正则化：当前的这些 Transformer 模型通常是在大规模语料库上进行预训练，然后在较小的下游任务上微调，而当微调数据集比较小时经常出现过拟合，而 Switch Transformer 这类 MoE 模型可能加剧过拟合的程度。为了缓解这一问题，作者增加了专家内部（FFN）的 Dropout 比例，称为专家 Dropout（Expert Dropout，ED）。然而，作者发现所有层增加 Dropout 率会导致性能更差；作者发现，在非专家层使用较小的 Dropout 率可以缓解这一问题：

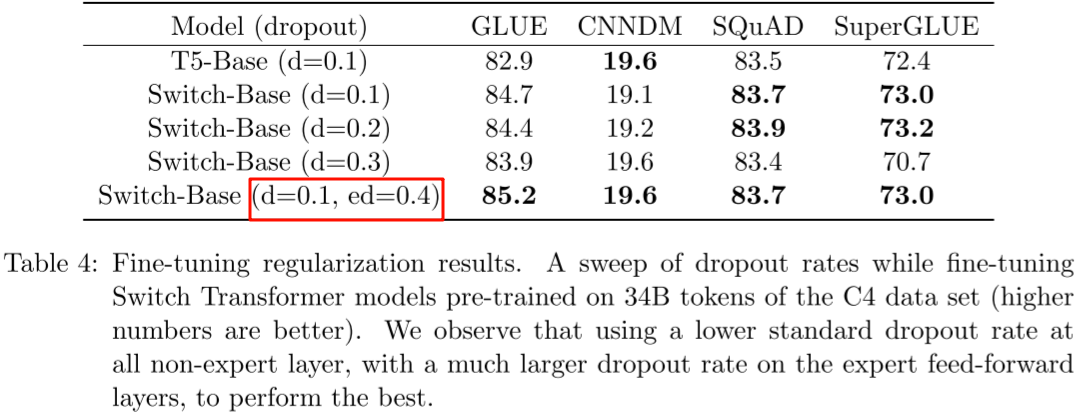
六、FastMoE

6.1 摘要

之前的高性能分布式 MoE 训练系统主要是针对 Google 的硬件（TPU）和软件（Mesh TensorFlow），并且不向公众开放，针对 NVIDIA GPU 和 Pytorch 还没有相应方案。

在 [2103.13262] FastMoE: A Fast Mixture-of-Expert Training System 中，作者提出 FastMoE，其是一个基于 Pytorch 的分布式 MoE 训练系统，并提供高度优化的高性能加速方案。该系统支持将不同的专家放置在多个节点上的多个 GPU 中，从而实现专家数量和 GPU 数量线性增加。

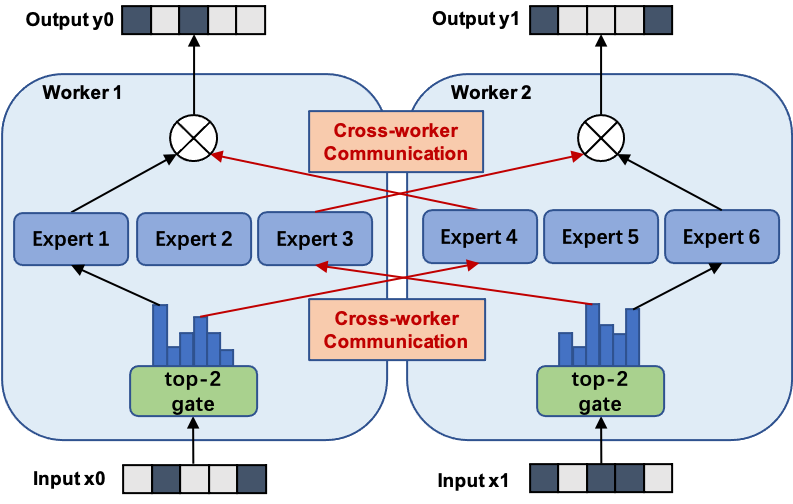
PS：如下图所示（来自 fastmoe/doc/readme-cn.md at master），FastMoE 主要针对的是 Expert 比较多的场景，也就是一个 GPU 上有 1 个或多个 Expert。在 2021 年底的 v0.3.0 版本中集成了 Megatron-LM，通过 Megatron-LM 的 Tensor Parallel 来实现一个 Expert 分布在不同的 GPU 上。

6.2 系统设计

6.2.1 灵活性

FastMoE 的灵活性主要体现在以下几个方面：

• 支持任意的网络作为专家。作者对专家模块做了抽象，用户可以专注设计专家模块；此外，FastMoE 也支持将多个专家放在同一个 Worker 上。

• 针对 Transformer 模型高度优化的 FFN。尤其是当多个专家放在一个 Worker 时，常见的方式是通过 for 循环串行的执行 Worker 上的多个专家，而作者实现了并行执行不同专家的方案。（Batched Gemm）

• 插件式支持 Pytorch 和 Megatron-LM。作者对 FastMoE 进行了必要的抽象，使其很容易与其他框架集成，如下图所示为与 Megatron-LM 集成的示例：

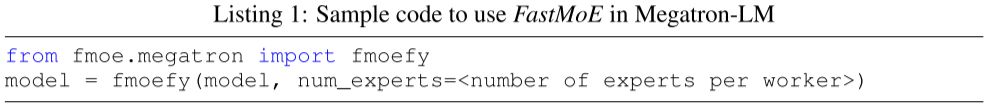
6.2.2 扩展模型容量

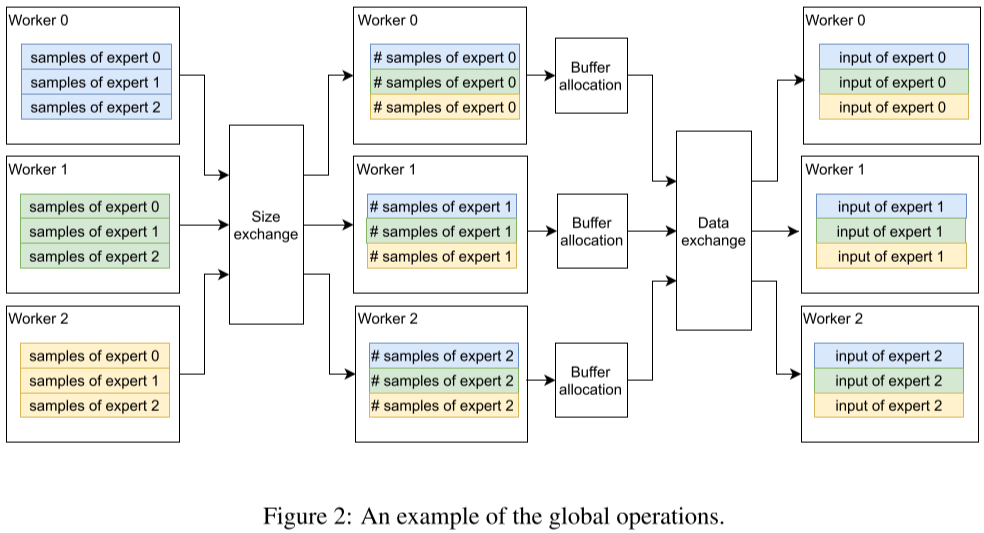
FastMoE 的模型并行方案。FastMoE 支持将专家分布在多个节点的多个 Worker 上，并且将不同 Worker 之间的数据通信隐藏起来，模型开发人员不用考虑。此外，在分布式 MoE 系统中的一个主要挑战为：动态路由导致分配给不同专家的输入样本数可能存在很大的差异。作者的方案为：在 Worker 之间交换实际的数据之前，先在 Worker 之间交换大小信息，Worker 根据相应信息分配 Buffer，然后传输真实的数据。

异构同步模块。模型的不同部分可能在不同的 Worker 组间重复，这非常有挑战，因为分布式模块不得不识别是否需要对参数的梯度进行同步，以及与谁同步。因此，FastMoE 引入了数据并行通信组标签：

• world：需要与所有 Worker 同步。

• data parallel：需要与模型并行组正交的数据并行组中的 Worker 同步。

• none：不需同步。

例如，无论模型并行设置如何，Gating Network 需要在所有 Worker 之间复制，因此标签为 world。注意力层可以划分为模型并行子层，因此其标签为 data parallel。每个 Worker 都包含几个特定的专家网络，其标签为 none。

6.3 优化激活

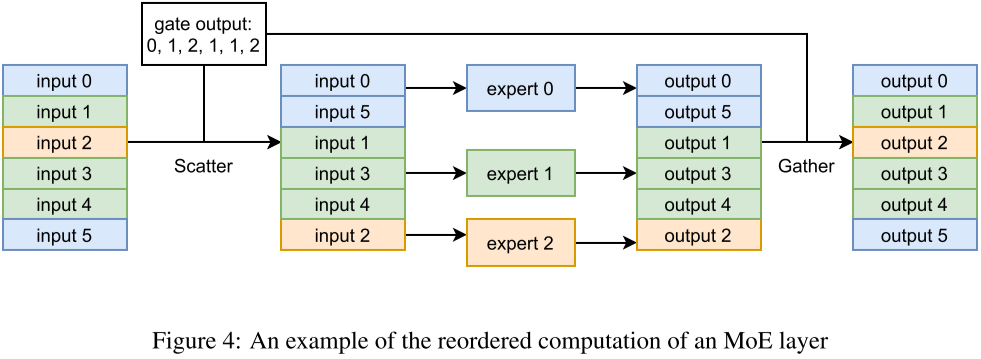
FastMoE 将所有输入样本一起 Batching 后发给同一个专家。由于数据表示的限制，FastMoE 使用专门开发的 CUDA Kernel 进行内存移动，以减少开销。如下图 Figure 4 所示，给定每个样本要进入的索引（Gating 输出），通过 Scatter 操作将所有样本按照对应顺序进行排布，执行完专家计算之后，再按照相反的 Gather 操作进行复原。（gate output 应该为 0, 1, 2, 1, 1, 0 ?）

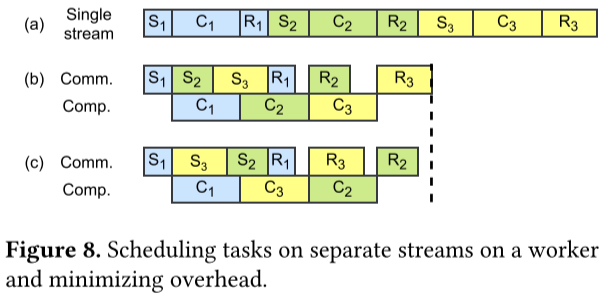
6.4 多 CUDA Stream 调度

如下图 Figure 8 所示，S 表示 Send，R 表示 Receive，C 表示 Compute，通过利用 CUDA 的 Multi Stream 机制，可以最大限度实现通信和计算的 overlap，实现加速的目的：

七、Tutel

7.1 摘要

之前的 MoE 分布式训练系统往往采用静态执行方式（Tensor 的 Shape 在执行中不能改变），导致经 Token 路由之后可能存在 Token 丢弃或者 Padding 无效计算的问题，导致计算效率比较低。

在 [2206.03382] Tutel: Adaptive Mixture-of-Experts at Scale 中，作者提出了 Tutel，其具备动态自适应并行和流水并行（PS：非流水线并行）机制。Tutel 中作者设计了一个统一布局来分发 MoE 模型参数和输入数据，并利用其实现可切换并行性和动态流水并行，而无需引入数学不等价操作或者 Tensor 迁移开销，可以在运行时以零成本实现自适应并行/流水并行优化。基于这一关键设计，Tutel 实现了各种 MoE 加速技术，包括 Flexible All-to-All、二维分层（2DH）All-to-All，以及快速编码、解码等。综合所有技术，Tutel 相比之前的方案，在 16 个和 2048 个 A100 GPU 上，单个 MoE 层的速度提升 4.96x 和 5.75x。

作者评估表明，Tutel 可以高效地运行 SwinV2-MoE，其基于 Swin Transformer V2 构建。使用 Tutel 训练和推理 SwinV2-MoE 比 Fairseq 加速 1.55x 和 2.11x。同时，SwinV2-MoE 在预训练及下游视觉任务中比对应的密集模型实现了更高的准确性。

7.2 自适应 MoE

鉴于 EP、DP 和 MP 派生了 7 种不同的并行方法组合，一种方案是为每种方法设计一个执行流程，并使其可与其他方法切换。然而，实际上没有必要设计 7 个执行流程，因为其可以简化为更小但效率相当的问题。作者的方法是分析所有并行方法的复杂性，以将它们缩小到最小子集（这里作者只考虑最重要的通信复杂性，所有 GPU 都执行相同的计算，计算复杂度相同，通信复杂性直接决定了一种并行方法相比其他方法的效率）。如果它们满足以下条件则将其删除：

1. 在任何情况下都不是最佳的。

2. 是另一种方法的特例。

如下图 Table 3 所示为一些常见的参数：

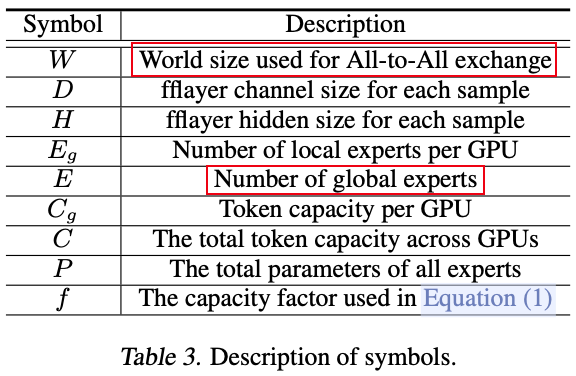
作者在参数表里没有具体介绍 r 参数，只在后文介绍，表示每个专家的 TP 数，也就是每个专家分布在几个 GPU 上：

• 如果 r=1，则表示 EP+DP+MP 变为 EP+DP

• 如果 r= W/E，则表示 EP+DP+MP 变为 EP+MP

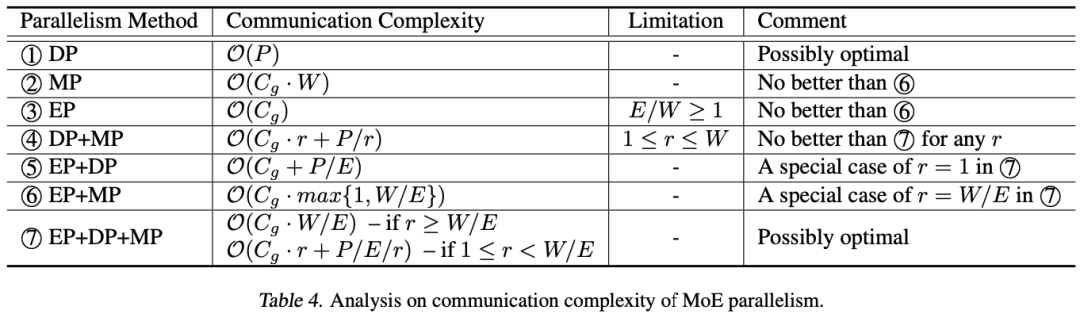
如下图 Table 4 所示，经过一系列比较，作者得出结论，该子集只包含 DP（1） 和 EP+DP+MP（7）：

• 对于 DP（1）：仅数据并行，不过采用的是 ZeRO-DP Stage-3，可以将模型参数分布在多个 GPU 设备，在前向计算的时候通过 All-Gather 操作获取所有模型参数进行计算。在反向时，执行一次 Reduce-Scatter。

• 对于 MP（2）：仅模型并行，每个 GPU 上都只有模型的 1/W，所有 GPU 加起来有一份完整模型。只要能使用 EP，则总会差于 EP+MP（6）。

• 对于 EP（3）：只有专家数量 >= GPU 数量才有意义，因此作者假设专家数量 < GPU 数量，这也是当前 LLM-MoE 的现状，不用考虑纯 EP 的方案。

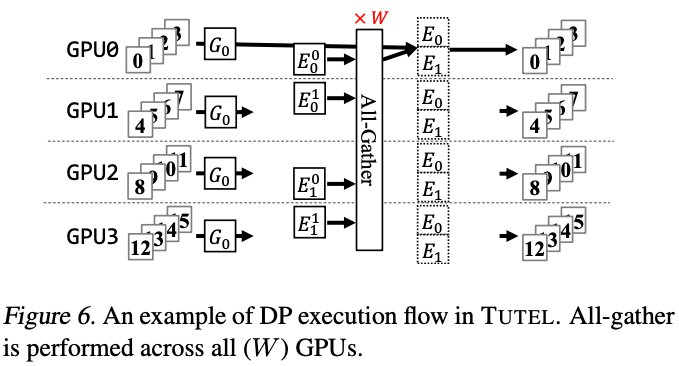
如下图 Figure 6 所示为相应的 Zero-DP，假设有 4 个 GPU，模型有 2 个专家，则每个 GPU 都只存储某个专家的 1/2。在前向计算时需要一次 All-Gather 获取到 2 个完整的专家参数。

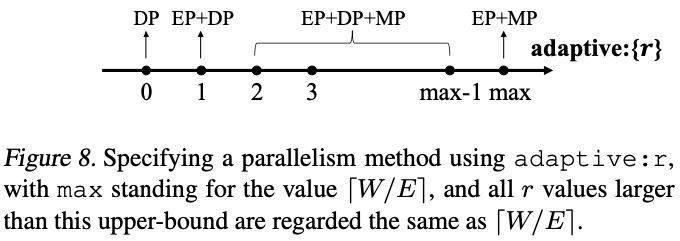
经过如上的分析后，作者得出了不同的分布式方案，如下图 Figure 8 所示，假设 ZeRO-DP 为 r=0，根据 r 的不同值可以选择不同的策略，特殊情况为上述介绍的 r=1 和 r=W/E：

7.3 优化

7.3.1 Flexible All-to-All

常规的 FFN 层计算时，All-to-All 的 data layout 会和 Word-Size 有关，当 Word-Size（GPU）数目比较大时，性能可能会下降比较多：

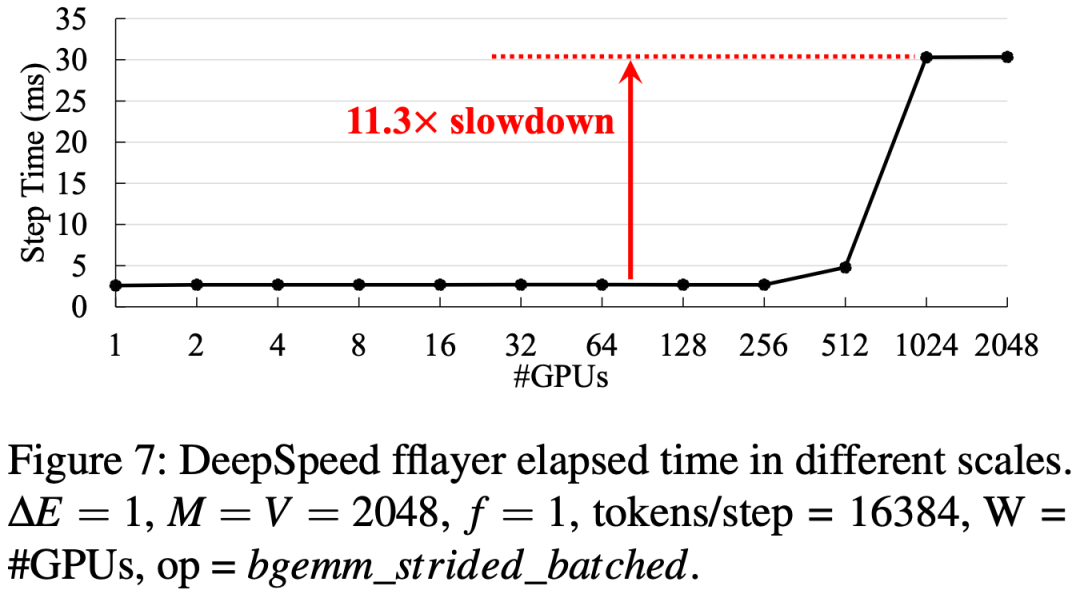
PS：出现这一问题的主要原因是：FFN layer 主要为矩阵乘法，GPU 处理大矩阵乘法非常高效，而如果矩阵中的某一维度比较小时，会导致矩阵乘法处于 Roofline-Model 的 Memory-Bound 区域，导致无法充分发挥 GPU 算力，并且维度越小此瓶颈越明显。当 World-Size 为 256 时，对应的矩阵短边为 16384/256=64，可能正好在 Roofline-Model 的转折点，这也是为什么当 Worhd-Size 进一步增大时性能会进一步降低。

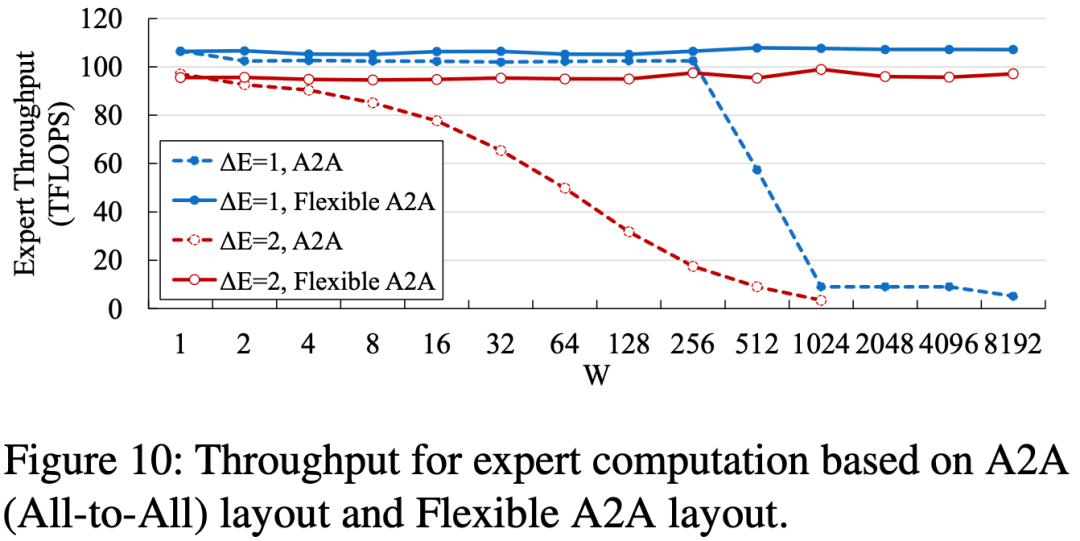
Flexible All-to-All 的目的是去除和 World-Size 的相关性，如下图为优化后的效果：

7.3.2 2DH All-to-All

如下图 Figure 15 所示，2DH All-to-All 的主要思路是充分考虑数据的局部性（GPU 内，同 node GPU、多 node GPU），将非连续内存空间对齐到连续内存空间，并将多个小的通信合并成大的通信：

• 第一列 -> 第二列：GPU 内部交换数据（无通信）

• 第二列 -> 第三列：同 node 的 GPU 间交换数据（NVLink）

• 第三列 -> 第四列：GPU 内部交换数据（无通信）

• 第四列 -> 第五列：跨 node 的 GPU 间交换数据（网络）

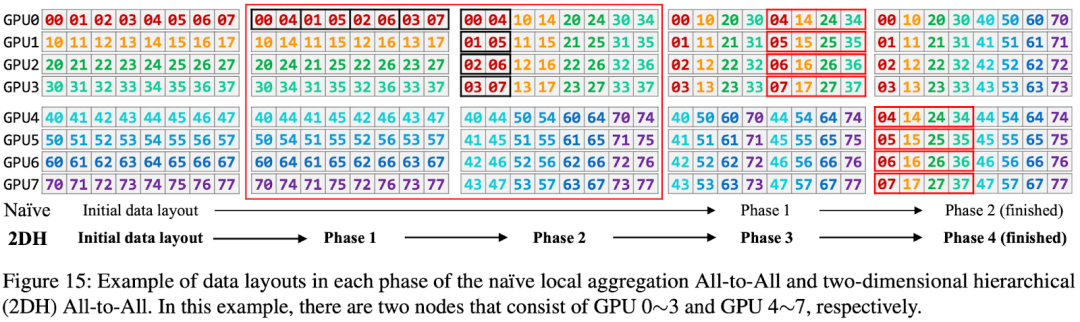
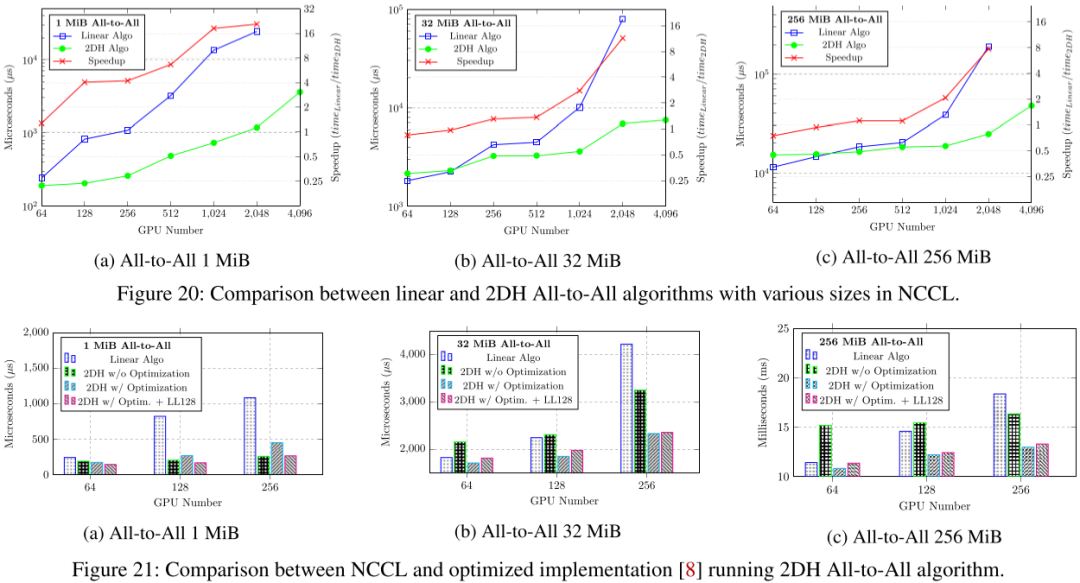
如下图 Figure 20 和 Figure 21 所示，提出的 2DH All-to-All 比基线提升明显：

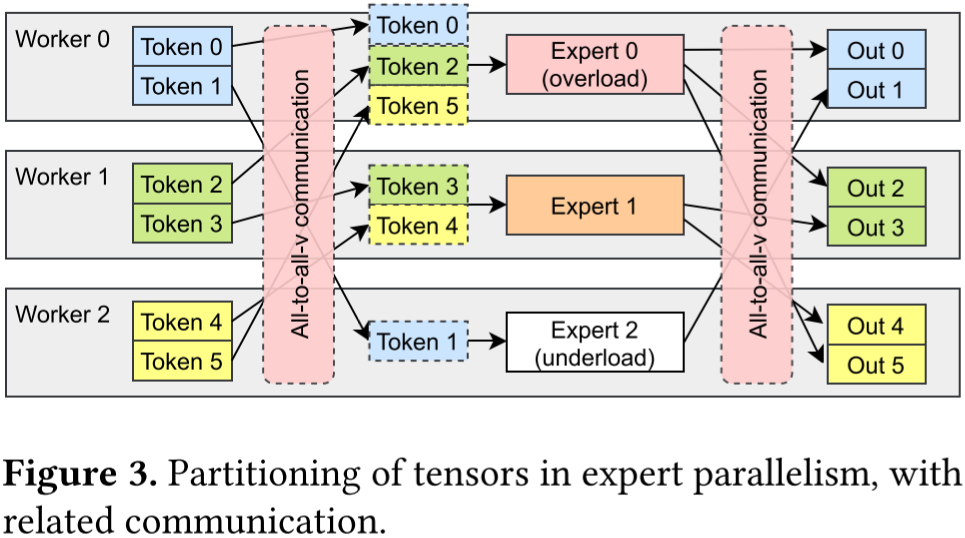
7.3.3 Fast Encode 和 Decode Kernel 优化

如下图 Figure 3 所示，在专家并行模式下，专家层的前后会分别引入 All-to-All 通信操作。前一个 All-to-All 用于将每个 Worker 上的 Token 按照 Router 后对应的专家发送到专家所在的 GPU，也叫 All-to-All（Dispatch）；而后一个 All-to-All 用于将专家计算后的 Token 重新按照原来的方式排列，也叫 All-to-All（Combine）。

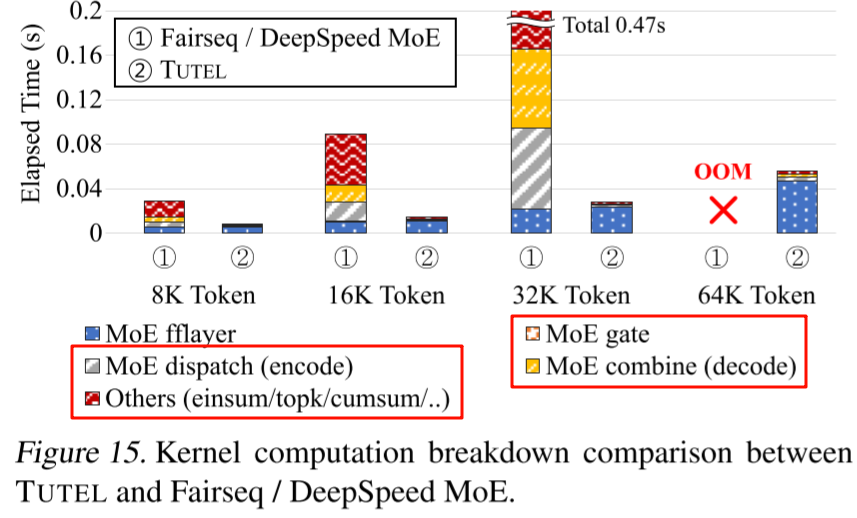
在 All-to-All（Dispatch）操作之前需要准备好 All-to-All 的输入，也叫 Encode；在 All-to-All（Combine）操作之后需要解包 All-to-All 的输出，组织为原始的顺序，也叫 Decode。而很多框架中 Encode 和 Decode 的实现都不够高效，有很多无效计算，因此作者定制了高性能 CUDA Kernel 来优化，如下图（a）为未优化的 Encode，（b）为优化后的 Encode。

如下图 Figure 15 所示，优化后 Encode、Decode 相关的时间大幅降低（此外也可以有效节约显存）：

7.3.4 Adaptive Pipelining

此外，在 Tutel 中，作者也采用了 Multi-Stream 机制来实现计算和通信的重叠，以提升效率，这里不再展开。

八、MegaBlocks

8.1 摘要

MegaBlocks（[2211.15841] MegaBlocks: Efficient Sparse Training with Mixture-of-Experts） 是斯坦福大学、微软及谷歌联合发布的在 GPU 上高效训练 MoE 的系统。之前我们提到过，MoE 的 Router 负载不均衡会导致需要删除 Token 或者 Padding 填充，本文中作者采用块稀疏操作对 MoE 计算进行了重新调整，并开发了新的块稀疏 GPU Kernel，以高效处理 MoE 中存在的动态性。作者提出的方法中从不丢弃 Token，并能与现有硬件很好地结合。

与最先进的 Tutel 库相比，端到端训练速度提高 40%；与使用高度优化的 Megatron-LM 框架训练的 DNN 相比，端到端训练速度提高 2.4x。

PS：需要说明的是，MegaBlocks 主要针对的还是单个 GPU 上包含多个专家的场景。

8.2 方法

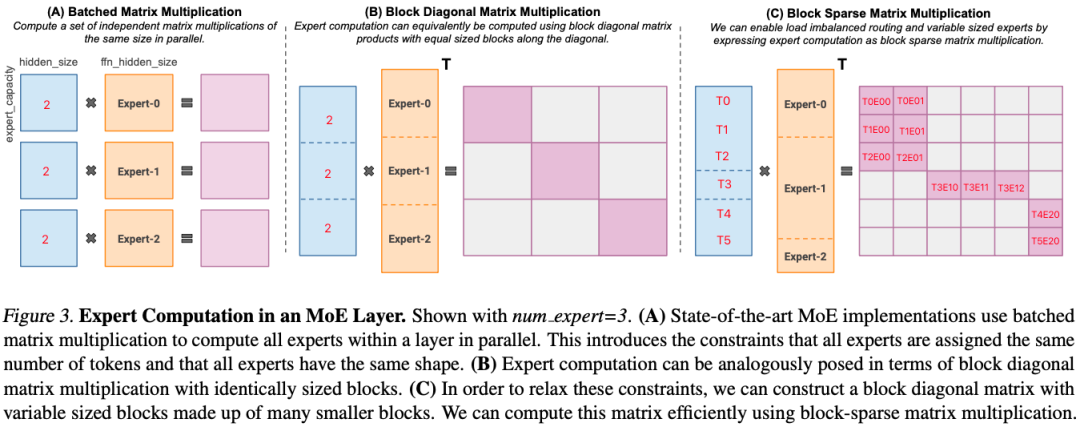
MegaBlocks 主要解决的是 1 个 GPU 上有多个专家时，由于负载不均衡导致的 Token 丢弃或者 Padding 无效计算问题。如下图 Figure 3 所示，假设有 3 个专家，每个专家的 Capability 为 2 个 Token，Router 后分配给 3 个专家的 Token 分别为 3,1,2，因此 Expert-0 需要丢弃一个 Token，Expert-1 需要 Padding 一个 Token。假设 Token Embedding 维度为 1024，FFN 第一个 MLP 升维后为 4096：

• （A）：对应 3 个 (2, 1024) 和 (1024, 4096) 的矩阵乘法，每个输出都是 (2, 4096)

• （B）：可以表示为 Batch Gemm 来计算，输出为 (6, 12288)，但只有对角线上有 3 个 (2, 4096) 的子矩阵，其他位置为 0。采用稀疏计算不会增加额外的计算量。

• （C）：同样可以表示为 Batch Gemm（可变 Shape），但是不丢弃 Token，也不 Padding，相当于 (3, 1024)，(1, 1024) 和 (2, 1024) 的 3 个矩阵分别不同的 (1024, 4096) 的矩阵相乘，稀疏表示后生成的还是 (6, 12288) 矩阵。PS：这个图很容易让人迷惑，图中的列分块是作者想要支持可变大小的专家，但并没有实现。实际上当前用的专家大小都相同，所以各个专家列分块的大小也应该相同。

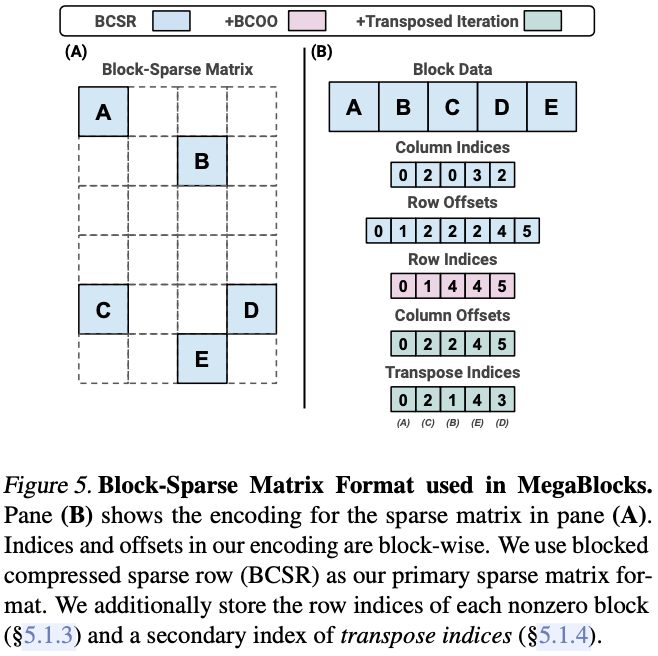
如下图 Figure 5 所示为对应的稀疏分块矩阵表示方式：

九、参考链接

1. https://github.com/xai-org/grok-1/tree/main

2. https://arxiv.org/abs/2101.03961

3. https://www.cs.toronto.edu/~hinton/absps/jjnh91.pdf

4. https://arxiv.org/abs/1701.06538

5. https://arxiv.org/abs/2006.16668

6. https://arxiv.org/abs/2101.03961

7. https://arxiv.org/abs/2103.13262

8. https://github.com/laekov/fastmoe/blob/master/doc/readme-cn.md

9. https://arxiv.org/abs/2206.03382

10. https://arxiv.org/abs/2211.15841

11. https://huggingface.co/blog/zh/moe

12. https://zhuanlan.zhihu.com/p/653518289