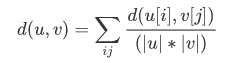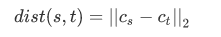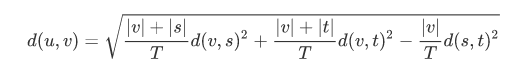- 1PAT 1059 C语言竞赛 (20 分)
- 2Python之web服务利器Flask生产环境部署实践【基于gunicorn部署生产环境】
- 3设计模式之桥接模式:Swift 实现_swift 桥梁模式
- 4汪老师分享 - 51单片机智能关窗控制系统设计_stc89c52单片机和lm393
- 5我们该使用哪种分布式锁?
- 6CogVLM2多模态开源大模型部署与使用_windows 部署 cogvlm2
- 7基于Matlab遗传算法的无人机和货车路径规划_遗传算法解决无人驾驶
- 8[油猴脚本开发指南]外部资源引用_油猴脚本token
- 9Centos7配置IP地址和DNS(转发)_centos ip addr add dns
- 10Windows安全基线加固实战_windows基线加固
Python层次聚类sci.cluster.hierarchy.linkage函数详解_scipy.cluster.hierarchy
赞
踩
1 函数原型:
scipy.cluster.hierarchy.linkage(y, method='single', metric='euclidean', optimal_ordering=False)函数功能:进行层次聚类/凝聚聚类。
参数:
y: 可以是1维压缩向量(距离向量),也可以是2维观测向量(坐标矩阵)。若y是1维压缩向量,则y必须是n个初始观测值的组合,n是坐标矩阵中成对的观测值。
返回值:(n-1)*4的矩阵Z(后面会仔细的讲解返回值各个字段的含义)
linkage方法用于计算两个聚类簇s和t之间的距离d(s,t),这个方法的使用在层次聚类之前。当s和t行程一个新的聚类簇u时,s和t被从森林(已经形成的聚类簇群)中移除,而用新的聚类簇u来代替。当森林中只有一个聚类簇时算法停止。而这个聚类簇就成了聚类树的根。
距离矩阵在每次迭代中都将被保存,d[i,j]对应于第i个聚类簇与第j个聚类簇之间的距离。每次迭代必须更新新形成的聚类簇之间的距离矩阵。
假定现在有|u|个初始观测值u[0],...,u[|u|-1]在聚类簇u中,有|v|个初始对象v[0],...,v[|v|-1]在聚类簇v中。回忆s和t合并成u。让v成为森林中的聚类簇,而不是u。
下面是计算新形成的聚类簇u和v之间距离的方法:
- method = ‘single’
d(u,v) = min(dist(u[i],u[j]))
对于u中所有点i和v中所有点j。这被称为最近邻点算法。
- method = 'complete'
d(u,v) = max(dist(u[i],u[j]))
对于u中所有点i和v中所有点j。这被称为最近邻点算法。
- method = 'average'
|u|,|v|是聚类u和v中元素的的个数,这被称为UPGMA算法(非加权组平均)法。
- method = 'weighted'
d(u,v) = (dist(s,v) + dist(t,v))/2
u是由s和t形成的,而v是森林中剩余的聚类簇,这被称为WPGMA(加权分组平均)法。
- method = 'centroid'
Cs和Ct分别为聚类簇s和t的聚类中心,当s和t形成一个新的聚类簇时,聚类中心centroid会在s和t上重新计算。这段聚类就变成了u的质心和剩下聚类簇v的质心之间的欧式距离。这杯称为UPGMC算法(采用质心的无加权paire-group方法)。
- method = 'median'
当两个聚类簇s和t组合成一个新的聚类簇u时,s和t的质心的均值称为u的质心。这被称为WPGMC算法。
- method = 'ward' (沃德方差最小化算法)
新的输入d(u,v)通过下式计算得出,
u是s和t组成的新的聚类,v是森林中未使用的聚类。T = |v|+|s|+|t|,|*|是聚类簇中观测值的个数。
注意:当最小距离在一个森林中成对存在时,即有多个最小距离的时候,具体的实现要看MATLAB的版本(因为这个函数是从matlab里面copy过来的)。
2 参数:
y:nump.ndarry。是一个压缩距离的平面上三角矩阵。或者n*m的观测值。压缩距离矩阵的所有元素必须是有限的,没有NaNs或infs。
method:str,可选。
metric:str或function,可选。在y维观测向量的情况下使用该参数,苟泽忽略。参照有效距离度量列表的pdist函数,还可以使用自定义距离函数。
optimal_ordering:bool。若为true,linkage矩阵则被重新排序,以便连续叶子间距最小。当数据可视化时,这将使得树结构更为直观。默认为false,因为数据集非常大时,执行此操作计算量将非常大。
Note:上述算法的时间复杂度如下:
| 算法 | 时间复杂度 |
| single | O(n2) |
| complete | O(n2) |
| average | O(n2) |
| weighted | O(n2) |
| ward | O(n2) |
| 其他 | O(n2) |
3 返回值:
Z:numpy.ndarry。
层次聚类编码为一个linkage矩阵。
Z共有四列组成,第一字段与第二字段分别为聚类簇的编号,在初始距离前每个初始值被从0~n-1进行标识,每生成一个新的聚类簇就在此基础上增加一对新的聚类簇进行标识,第三个字段表示前两个聚类簇之间的距离,第四个字段表示新生成聚类簇所包含的元素的个数。
下面举个例子来说明一下:
- #%%
- from scipy.cluster.hierarchy import dendrogram, linkage,fcluster
- from matplotlib import pyplot as plt
- X = [[i] for i in [2, 8, 0, 4, 1, 9, 9, 0]]
- # X = [[1,2],[3,2],[4,4],[1,2],[1,3]]
- Z = linkage(X, 'ward')
- f = fcluster(Z,4,'distance')
- fig = plt.figure(figsize=(5, 3))
- dn = dendrogram(Z)
- plt.show()
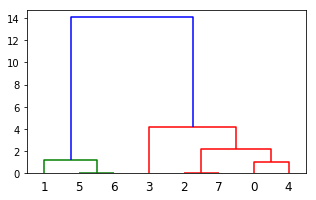
下面是聚类结果的可视化聚类树:
下面是返回值的解析:
2018/2/25凌晨1点
推荐一个视频自学网站:
[url=http://www.51zxw.net/study.asp?vip=16791798 【51自学网】-专业培训老师录制的视频教程,让学习变得很轻松[/url]