有趣的微分方程之欧拉方程_欧拉方程微分方程详解

作者：代码探险家 | 2024-07-12 12:07:30

踩

欧拉方程微分方程详解

欧拉欧拉，千古神话。
不得不说，欧拉带给我们的惊喜实在是太多太多。就比如欧拉公式
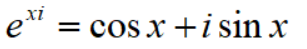
在这里插入图片描述
哇哦，多么漂亮的一个式子。
这次我们来看看欧拉的另一个惊喜，欧拉微分方程（属于可通过变量替换由变系数微分方程化为常系数微分方程的一类）。
形式如下：

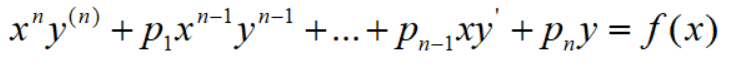
做变量替换，x=e^t（x>0,若x<0,可令x=-e^t） ,然后把所有的y对x的求导转换为y对t的求导，如下：
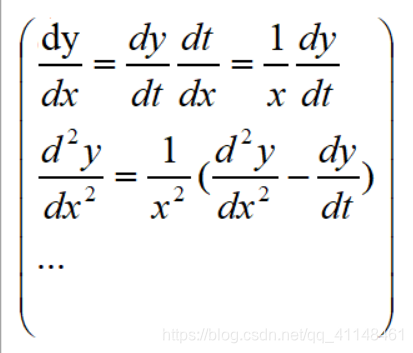
在这里插入图片描述
用记号D表示对t的求导运算d/dt,那么上述结果可以简化为：

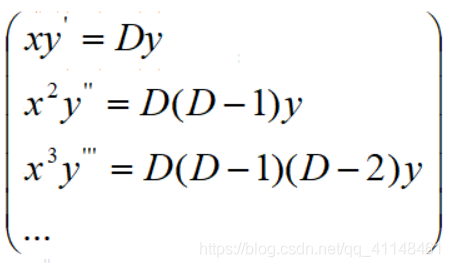
一般有：

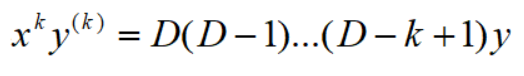
代入原方程，便得一个以t为自变量的常系数微分方程，求出这个方程后，进行逆替换，便得原方程的解。
待续。。

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/代码探险家/article/detail/814062