2.6 矩阵的分块_如何对矩阵分块

 

2.6 矩阵的分块

矩阵分块是一种将矩阵划分为若干子矩阵的方法。这种方法在矩阵运算中非常有用，可以简化计算并提高运算效率。

2.6.1 分块矩阵

分块方法示例

例如，对于矩阵 AAA:

我们可以将其按照如下方式进行分块：

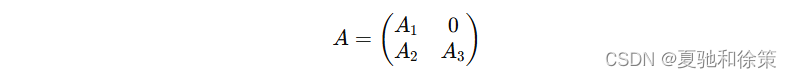
其中：

矩阵的分块方法有很多种，没有一个通用的标准。对于矩阵分块后的运算，有与通常矩阵运算完全类似的运算法则，但有两点需要特别注意：一是必须保证相关运算有意义，二是保证分块有利于简化运算。

例子分析

例 2.38

直接验证容易证明，若 A=(A100A2)A =

$$\begin{pmatrix} A_1 & 0 \\ 0 & A_2 \end{pmatrix}$$ A=(A1​0​0A2​​)，其中 A1A_1A1​ 和 A2A_2A2​ 都是可逆的方阵，则：

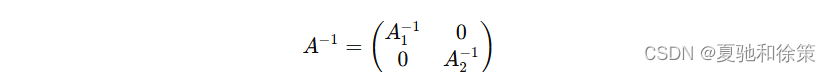
例 2.39

设 AAA 和 BBB 分别为 mmm 阶和 nnn 阶可逆矩阵。证明 (A00B)

$$\begin{pmatrix} A & 0 \\ 0 & B \end{pmatrix}$$ (A0​0B​) 可逆，并求其逆矩阵。

证明：

构造分块矩阵，并对其实施初等变换可得：

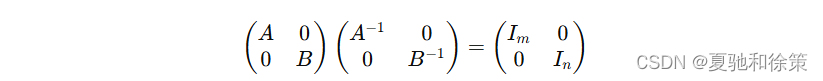
因此，矩阵可逆，且：

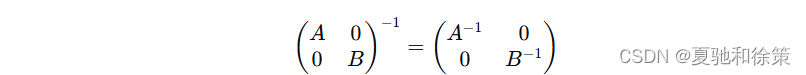
例 2.40

设 AAA 可逆，并求 A−1A^{-1}A−1。

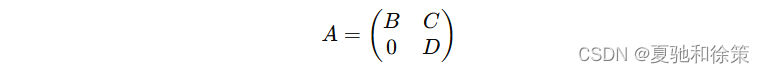
证明由 ∣A∣=∣B∣∣D∣≠0|A| = |B||D| \neq 0∣A∣=∣B∣∣D∣=0 知 AAA 可逆。设 X,TX, TX,T 分别是与 B,DB, DB,D 同阶的方阵。于是由：

得：

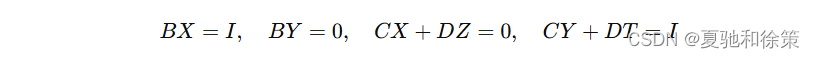
由此得：

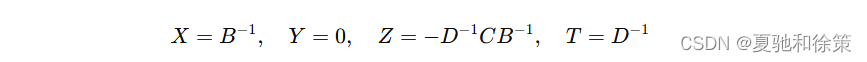
于是：

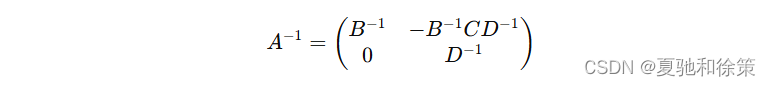
2.6.2 分块矩阵的初等变换

类似于通常矩阵的初等变换，我们可以定义分块矩阵的初等变换。分块矩阵的初等变换也有三种类型：

1. 交换分块矩阵的两行（列）；
2. 用一个适当阶数的可逆矩阵左（右）乘分块矩阵的某一行（列）的各子块；
3. 将分块矩阵的某一行（列）的各子块加上一个适当行数和列数的矩阵左（右）乘分块矩阵的另一行（列）所对应的子块。

在具体运算过程中，需要注意两点：一是所有运算必须有意义；二是初等行变换只能是在某一行（列）左乘一矩阵，初等列变换只能是在某一行（列）右乘一矩阵。

例子分析

例 2.42

设分块矩阵 P=(AB0C)P =

$$\begin{pmatrix} A & B \\ 0 & C \end{pmatrix}$$ P=(A0​BC​)，其中 AAA 和 CCC 分别是 mmm 阶和 nnn 阶可逆矩阵，BBB 为 m×nm \times nm×n 矩阵。证明 PPP 可逆，并求 P−1P^{-1}P−1。

证明：

类似于元素为实数的矩阵的求逆方法，构造如下分块矩阵，并对其实施初等变换：

因此，矩阵 PPP 可逆，且：

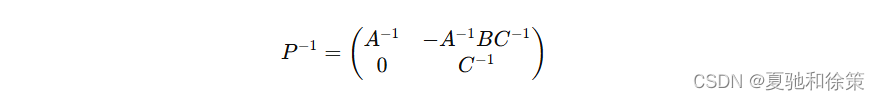
例 2.43

证明：可逆上三角矩阵的逆矩阵仍然是上三角矩阵。

证明：

对 nnn 阶矩阵 AAA 的阶数用数学归纳法。

当 n=1n=1n=1 时结论显然成立。设 n=k−1n=k-1n=k−1 时结论成立。将可逆的上三角矩阵 AkA_kAk​ 按如下形式分块：

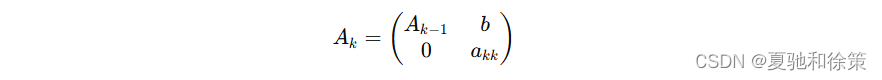
其中 Ak−1A_{k-1}Ak−1​ 为 k−1k-1k−1 阶上三角矩阵。易知 akk≠0a_{kk} \neq 0akk​=0，Ak−1A_{k-1}Ak−1​ 可逆。由归纳假设，Ak−1A_{k-1}Ak−1​ 的逆矩阵仍为上三角矩阵。因此 Ak−1A_k^{-1}Ak−1​ 也是上三角矩阵。由归纳法可知结论成立。

结论

矩阵的分块方法在矩阵运算中具有重要意义。通过分块矩阵的运算和初等变换，可以简化计算过程，提高计算效率。希望本文能够帮助你更好地理解矩阵分块及其运算方法，为你的学习和应用提供帮助。