java递归内存_Java递归方法

Java递归方法

什么是方法递归？我们先来看一段代码：

public class RecursionTest01 {

public static void main(String[] args) {

m();

}

public static void m(){

System.out.println("m begin");

m();

System.out.println("m over");

}

}

以上代码的执行结果如下图所示：

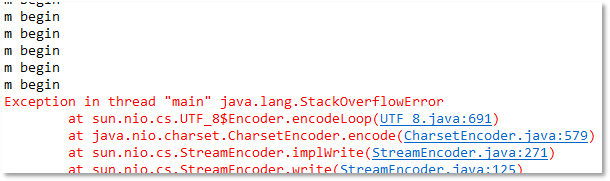
图7-17：递归执行结果

我们可以看到以上代码的执行过程中，一直输出“m begin”，“m over”一次也没有输出，直到最终发生了错误：java.lang.StackOverflowError，这个错误是栈内存溢出错误，错误发生后，JVM退出了，程序结束了。

实际上以上代码在m()方法执行过程中又调用了m()方法，方法自身调用自身，这就是方法递归调用。以上程序实际上等同于以下的伪代码(说明问题，但是无法执行的代码)：

图7-18：说明递归执行原理的伪代码

通过伪代码我们可以看出，m()方法一直在被调用(方法中的代码必须遵循自上而下的顺序依次逐行执行，不能跳行执行)，对于栈内存来说一直在进行压栈操作，m()方法从未结束过，所以没有弹栈操作，即使栈内存足够大(也是有限的内存)，总有一天栈内存会不够用的，这个时候就会出现栈内存溢出错误。通过以上研究得出递归必须要有合法的结束条件，没有结束条件就一定会发生StackOverflowError。我们再来看看有结束条件的递归，例如以下代码：

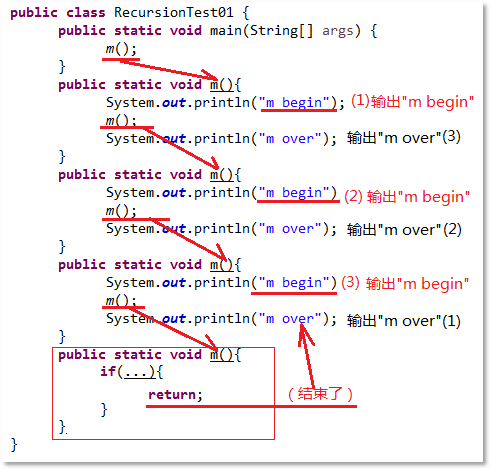
图7-19：递归的过程中满足了某个条件，递归结束了

综上所述，递归其实就是方法在执行的过程中调用了另一个方法，而另一个方法则是自己本身。在代码角度来看就是在a()方法中调用a()方法，使用递归须谨慎，因为递归在使用的时候必须有结束条件，没有结束条件就会导致无终止的压栈，栈内存最终必然会溢出，程序因错误的发生而终止。

大家再来思考一个问题，一个递归程序有合法有效的结束条件就一定不会发生栈内存溢出错误吗？在实际开发中遇到这个错误应该怎么办？

一个递归程序有的时候存在合法有效的终止条件，但由于递归的太深，在还没有等到条件成立的时候，栈内存已经发生了溢出，这种情况也是存在的，所以实际开发中我们尽可能使用循环来代替递归算法，原则是：能不用递归尽量不用，能用循环代替的尽可能使用循环。当然，如果在开发中遇到了由于使用递归导致栈内存溢出错误的发生，首先，我们要检查递归的终止条件是否合法，如果是合法的还是发生栈内存溢出错误，那么我们可以尝试调整堆栈空间的大小。怎么调整堆栈大小呢，大家可以研究一下下图中的一些参数，这里就不再讲解内存大小的调整了，这不是初级程序员应该掌握的。

图7-20：java虚拟机内存设置参数

接下来我们来研究一下在不使用递归的前提下，完成1~N的求和，这个应该很简单，请看下面代码：

public class RecursionTest02 {

public static void main(String[] args) {

int n = 5;

int result = accumulate(n);

System.out.println("1到" + n + "的和是：" + result);

}

public static int accumulate(int n){

int result = 0;

for(int i = 1;i <= n; i++){

result += i;

}

return result;

}

}

运行结果如下图所示：

图7-21：不使用递归计算1~N的和

那么，使用递归应该怎么写呢？请看以下代码：

public class RecursionTest03 {

public static void main(String[] args) {

int n = 5;

int result = accumulate(n);

System.out.println("1到" + n + "的和是：" + result);

}

public static int accumulate(int n){

if(n == 1){

return 1;

}

return n + accumulate(n - 1);

}

}

运行结果如下图所示：

图7-22：使用递归计算1~N的和

我们来使用伪代码对以上代码的执行过程进行分析，请看以下伪代码：

public static int accumulate(int n){ //假设n是5

if(n == 1){

return 1;

}

return n + accumulate(n - 1);

//return 5 + accumulate(4); return 5 + 4 + 3 + 2 + 1;

}

public static int accumulate(int n){

if(n == 1){

return 1;

}

return n + accumulate(n - 1);

//return 4 + accumulate(3);return 4 + 3 + 2 + 1;

}

public static int accumulate(int n){

if(n == 1){

return 1;

}

return n + accumulate(n - 1);

//return 3 + accumulate(2);return 3 + 2 + 1;

}

public static int accumulate(int n){

if(n == 1){

return 1;

}

return n + accumulate(n - 1);

//return 2 + accumulate(1);return 2 + 1;

}

public static int accumulate(int n){

if(n == 1){

return 1; //这行代码执行了return 1;

}

}

以上程序的内存变化是这样的，请看下图：

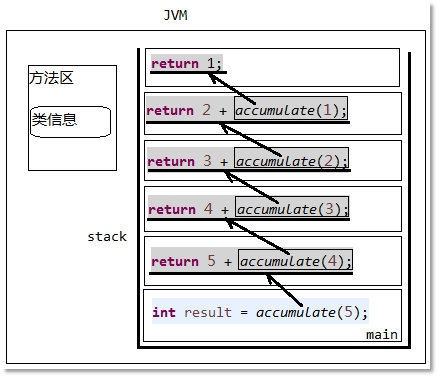
图7-23：1~N递归求和内存图

为了加强大家对递归算法的理解，我们再来看一张图：

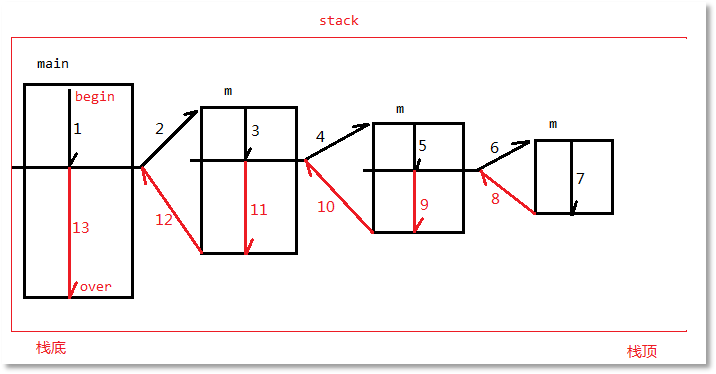
图7-24：另一种形式的递归内存图

其实大家把上图逆时针旋转90度，你会看到一个栈数据结构对吗？