现代雷达系统分析与设计---动目标检测(MTD)_雷达动目标检测

MTD是一种利用多普勒滤波器组来抑制各种杂波，以提高雷达在杂波背景下检测运动目标能力的技术。与MTI相比，MTD在如下方面进行了改善和提高。

1. 增大信号处理的线性动态范围
2. 使用一组多普勒滤波器，使之更接近于最佳滤波器，提高改善因子
3. 能抑制地杂波(其平均多普勒频移通常为零)，且能同时抑制运动杂波(如云雨、鸟群、箔条等)
4. 增加一个或多个杂波图，对于检测地物杂波中的低速目标甚至切向飞行大目标更有利

根据最佳滤波理论，在噪声与杂波背景下检测运动目标是一个广义匹配滤波问题。最佳滤波器应由白化滤波器级联匹配滤波器构成。白化滤波器将杂波(有色高斯白噪声)变成高斯白噪声，匹配滤波器使输出信噪比达到最大，如下图所示。

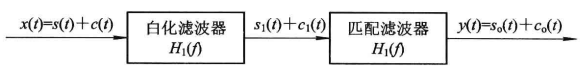
假设杂波功率谱$C(f)$和信号频率$S(f)$已知，根据匹配滤波器的定义有

$H_2(f)=S_1^{\ast }(f)e^{-j2\pi f{t}_s}=H_1^{\ast }(f)S^{\ast }(f)e^{-j2\pi f{t}_s}$

式中，$t_s$表示匹配滤波器输出到最大值的时延。白化滤波器使杂波输出$c_1(t)$的功率谱变为1，使得$c_1(t)$成为白噪声，即

$C(f)|H_1(f){|}^2=1$

白化滤波器功率传输函数为

$|H_1(f){|}^2=\frac{1}{C(f)}$

因此，广义匹配滤波器的传递函数为

$H(f)=H_1(f)H_2(f)=\frac{S^{\ast }(f)}{C(f)}{e}^{-j2\pi f{t}_s}$

可以粗略地认为，其中$H_1(f)$用来抑制杂波。对MTI而言，它要使杂波得到抑制而让各种速度的运动目标信号通过，所以$H_1(f)$相当于MTI滤波器，如下图(a)所示；$H_2(f)$用来对雷达回波脉冲串信号匹配。对单个脉冲而言，和目标信号匹配可以中频带通放大器来实现，而对脉冲串则只能采用对消后的非相参积累，所以实际中的MTI滤波器，只能使其滤波器的凹口对准杂波谱中心，且使二者宽度基本相等，有时也将这称为杂波抑制准最佳滤波。对于相参脉冲串，$H_2(f)$可以进一步表示为

$H_2(f)=H_{21}(f)H_{22}(f)$

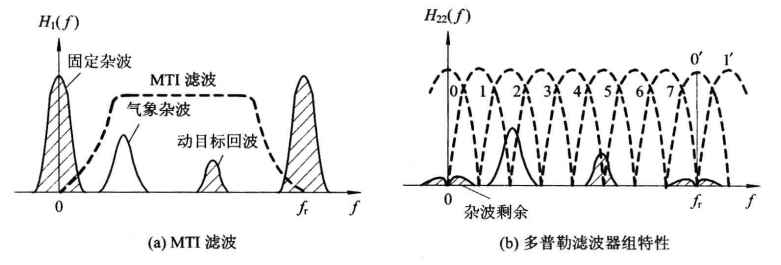
即信号匹配滤波器由$H_{21}(f)$和$H_{22}(f)$两个滤波器级联，式中，$H_{21}(f)$为单个脉冲的匹配滤波器，通常在接收机中放实现；$H_{22}(f)$对相参脉冲串进行匹配，他利用了回波脉冲串的相参性进行相参积累。$H_{22}(f)$是梳齿形滤波器，齿的间隔为脉冲重复频率$f_r$，如下图(b)所示，齿的位置取决于回波信号的多普勒频移，而齿的宽度应和回波谱线的宽度一致。

要对回波相参脉冲串进行匹配滤波，必须知道目标的多普勒频移以及天线扫描对脉冲串的调制情况，由于实际中$f_d$不能预知，因此要采用一组相邻且部分重叠的滤波器组，如下图(b)中的$0-7$号滤波器，覆盖整个多普勒频率范围，其中第5通道输出的就是动目标回波，这就是窄带多普勒滤波器组所要完成的功效。

设计MTD滤波器组的方法有两类：一类是MTI级联FFT的方法；另一类是优化的MTD滤波器组

MTI级联FFT的滤波器组

MTI级联FFT的MTD滤波器组是在FFT之前接一个二次对消器，它可以滤去最强的地物杂波，这样就可以减少窄带滤波器组所需要的动态范围，并降低对滤波器副瓣的要求。由于DFT是一种特殊的横向滤波器，所以滤波器组的系数可以按照DFT的定义来选择，并采用快速算法FFT来实现MTD滤波。

FFT的每点输出，相当于N点数据在这个频率上的积累，也可以说是以这个频率为中心的一个带通滤波器的输出。

根据DFT的定义，N组滤波器的权值为

$w_{nk}=e^{-j2\pi nk/N}，n=0,1,\dots \dots ,N-1;k=0,1,\dots \dots ,N-1$

式中，n表示第n个抽头，$k$表示第$k$个滤波器，每一个$k$值决定一个独立的滤波器响应，相应地对应于一个不同的多普勒滤波器响应。因此，第$k$个滤波器的频率响应函数为

$H_k(f)={\sum }_{n=0}^{N-1}{e}^{-j2\pi nk/N}{e}^{-j2\pi kf{T}_r}={\sum }_{n=0}^{N-1}{e}^{-j2\pi n(k/N+f{T}_r)}=e^{-j\pi (N-1)(k/N+f{T}_r)}\frac{sin[\pi N(k/N+f{T}_r)]}{sin[\pi (k/N+f{T}_r)]}$

滤波器的幅频特性为：

$|H_k(f)|=\frac{sin[\pi N(k/N+f{T}_r)]}{sin[\pi (k/N+f{T}_r)]}$

各滤波器具有相同的幅度特性，均为辛克函数，且等间隔地分布在频率轴上。滤波器地峰值产生于$sin[\pi (k/N+f{T}_r)]$或者$\pi (k/N+f{T}_r)=0{,}_{-}^{+}\pi {,}_{-}^{+}2\pi ,\dots \dots ,$当$k=0$时，滤波器峰值位置为$f=0{,}_{-}^{+}1/T_r{,}_{-}^{+}2/T_r,\dots \dots ,$即该滤波器地的中心位置在零频以及重复频率的整数倍处，因此对地杂波没有抑制能力。当$k=1$时，峰值响应产生在$\frac{1}{N{T}_r}$以及$f=\frac{1}{N{T}_r}、{\frac{1}{T_r}}_{-}^{+}\frac{1}{N{T}_r}、{\frac{2}{T_r}}_{-}^{+}\frac{1}{N{T}_r}$处，对$k=2$时，峰值响应产生在$f=\frac{2}{N{T}_r}$处，依次类推。每个滤波器的主副瓣比只有13.2dB，限制了它对气象杂波的抑制性能，需要使用更低副瓣的多普勒滤波器组。

为了降低副瓣，一般都需要加窗。目前常用的窗函数为海明窗(Hamming)，加窗可降低副瓣电平，但各滤波器的主瓣有一定展宽。

代码：

N = 12;
win = taylorwin(12);
f = (-0.1:0.01:1.1);
for m = 1:N
    ww(m,:) = exp(-1i*2*pi*m*(0:N-1)/N) .* win';
end

hd = ww * exp(-1i * 2 * pi * (0:N-1)' * f);
Hd = 20 * log10(abs(hd));

figure;
plot(f,Hd);
xlabel('归一化频率f/fr');
ylabel('幅度响应/dB');
xlim([min(f) max(f)]);
ylim([-80 30]);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

运行结果：

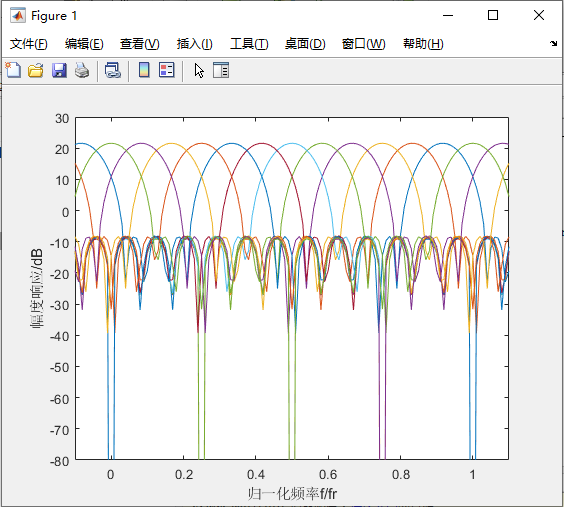
优化MTD滤波器组

由于对消器滤波特性的影响，MTI+FFT的合成多普勒滤波器组中各滤波器的主瓣有明显变形，各合成多普勒滤波器的杂波抑制性能各不相同。如果根据杂波抑制要求，直接设计一组具有更好杂波抑制性能的多普勒滤波器组，来代替对消级联FFT形式的MTD滤波器组，可进一步提高MTD处理器性能。

点最佳多普勒滤波器

点最佳多普勒滤波器组只在所需的多普勒处理频段中某一点上达到最佳，而在其它频率点都是不匹配的。多普勒滤波器就是用许多滤波器填满感兴趣的多普勒区域。通常实际应用中多普勒滤波器采用N点FIR滤波器填满多普勒区域，N等于处理的相干脉冲数。如下图所示：

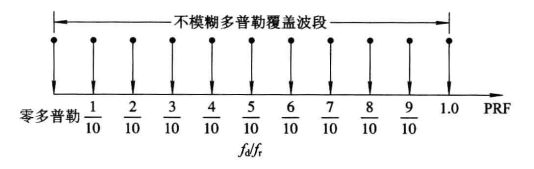
点多普勒横向滤波器复数输入信号表示为

$s_n=A{e}^{j{\omega }_{d}t}{\sum }_{n=0}^{N-1}\delta (t-n{T}_r)$

式中，A是幅度，${\omega }_d$是多普勒频率，N是相参脉冲数，$T_r$是雷达重复周期。信号矢量则可表示为$s=(s_1,s_2,\dots \dots ,s_N{)}^T$，其中，$s_n=A{e}^{j{\omega }_d(n-1)T_r},(n=1,2,\dots \dots ,N),R_s为归一化信号协方差矩阵$。

根据自适应滤波器原理，长度为N的滤波器中的第$k$个滤波器的权矢量为

$w_k=R^{-1}a(f_k)$

式中$f_k(k=1,2,\dots \dots ,K)$为第k个滤波器的通带中心频率，$a(k)$为导频矢量

$a(f_k)=[1,e^{j2\pi f_k{T}_r},e^{j2\pi f_{k}2T_r},\dots \dots ,e^{j2\pi f_k(N-1)T_r}{]}^T$

$R=R_c+{\delta }^{2}I$为杂波加噪声协方差矩阵，$R_c$为杂波协方差矩阵，I为单位矩阵(假设噪声为白噪声)，${\delta }^2$为噪声功率。$R^{-1}$的作用就是使滤波器自适应地在杂波频率处形成零陷，从而抑制杂波。

除了求出最佳加权，还必须确定改善因子的表达式。首先注意到信号协方差矩阵$R_s$的秩为1，因为这是矩阵中最大非零行列式的阶数。由于两个矩阵乘积的秩小于等于这两个矩阵中的任何一个，这意味着$R_c^{-1}{R}_s$的秩也为1。又因为非零特征值的个数等于矩阵的秩，故$R_c^{-1}{R}_s$只有一个非零特征值，必定等于改善因子，因此

$I=Trace(R_c^{-1}{R}_s)$

式中，$Trace(\bullet )$表示矩阵求迹

这样设计得到的自适应MTD滤波器会有较高的旁瓣电平，这样容易造成不同滤波器的目标之间的相互影响，会带来虚警；另外，进入滤波器副瓣的杂波(包括地杂波的剩余和气象杂波)也会降低滤波器的杂波改善性能。所以，需要对常规自适应MTD滤波器进行加权以降低各滤波器的副瓣电平。由于$R^{-1}$的存在，使得窗函数对MTD滤波器系数进行加权只能满足通带远离杂波较远的滤波器的要求，而不能使所有滤波器都达到要求。因此不能使用窗函数的方法来降低副瓣。

代码：

mtdjie = 12; %滤波器长度
fr = 100; %脉冲重复频率 Hz
df = 0.64; %杂波谱宽 Hz
T = 1/fr; %重复周期
N = mtdjie; %滤波器阶数
f = (-0.1*fr:0.1:1.1*fr);
for m = 1:mtdjie
    Rn(m,:) = exp(-2 * pi ^ 2 * df ^ 2 * ((m - (0:mtdjie - 1)) * T) .^ 2); %杂波自相关矩阵
end
Rn = Rn + 1e-6 * eye(mtdjie, mtdjie);
Rni = inv(Rn);
ww = zeros(N-1, mtdjie);
for m = 1:N-1
    s = exp(1i * 2 * pi * (0:mtdjie - 1) * m / N); %点最佳
    w0 = Rni * s.'; %最佳权值
    ww(m,:) = w0 ./ max(abs(w0)); %归一化
end
hd = ww * exp(-1i * 2 * pi * (0:mtdjie-1)' * T * f);
Hd = 20 * log10(abs(hd));
figure;
plot(f./fr, Hd);
xlabel('归一化频率 f/fr');
ylabel('幅度响应/dB');
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

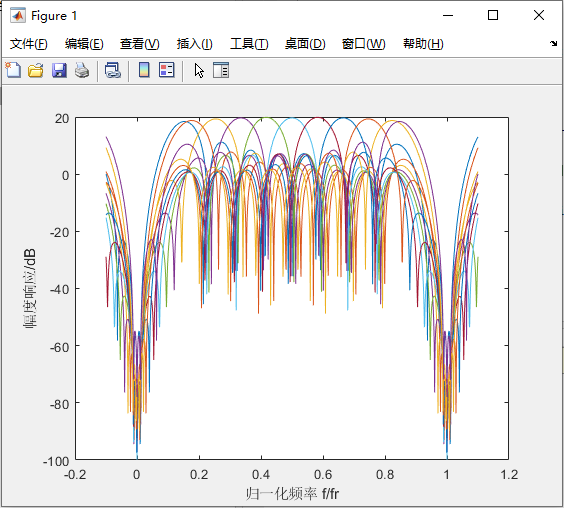
运行结果：

参考文献：

1. 《现代雷达系统分析与设计》，陈伯孝