几种常用的排序算法（c语言实现）_排序方法有哪几种

概述

最近重新回顾了一下数据结构和算法的一些基本知识，对几种排序算法有了更多的理解，也趁此机会通过博客做一个总结。

---

1.选择排序-简单选择排序

选择排序是最简单的一种基于O（n2）时间复杂度的排序算法，基本思想是从i=0位置开始到i=n-1每次通过内循环找出i位置到n-1位置的最小（大）值。

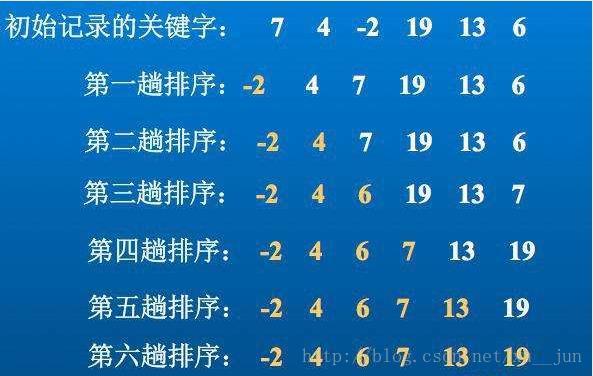
算法实现：

void selectSort(int arr[], int n)
{
    int i, j , minValue, tmp;
    for(i = 0; i < n-1; i++)
    {
        minValue = i;
        for(j = i + 1; j < n; j++)
        {
            if(arr[minValue] > arr[j])
            {
                minValue = j;
            }
        }
        if(minValue != i)
        {
            tmp = arr[i];
            arr[i] = arr[minValue];
            arr[minValue] = tmp;
        }
    }
}

void printArray(int arr[], int n)
{
    int i;
    for(i = 0; i < n; i++)
    {
        printf("%d ", arr[i]);
    }
    printf("\n");
}

void main()
{
    int arr[10] = {2,5,6,4,3,7,9,8,1,0};
    printArray(arr, 10);
    selectSort(arr, 10);
    printArray(arr, 10);
    return;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

如实现所示，简单的选择排序复杂度固定为O(n2)，每次内循环找出没有排序数列中的最小值，然后跟当前数据进行交换。由于选择排序通过查找最值的方式排序，循环次数几乎是固定的，一种优化方式是每次循环同时查找最大值和最小值可以是循环次数减少为（n/2），只是在循环中添加了记录最大值的操作，原理一样，本文不再对该方法进行实现。

---

2.冒泡排序

冒泡排序在一组需要排序的数组中，对两两数据顺序与要求顺序相反时，交换数据，使大的数据往后移，每趟排序将最大的数放在最后的位置上，如下：

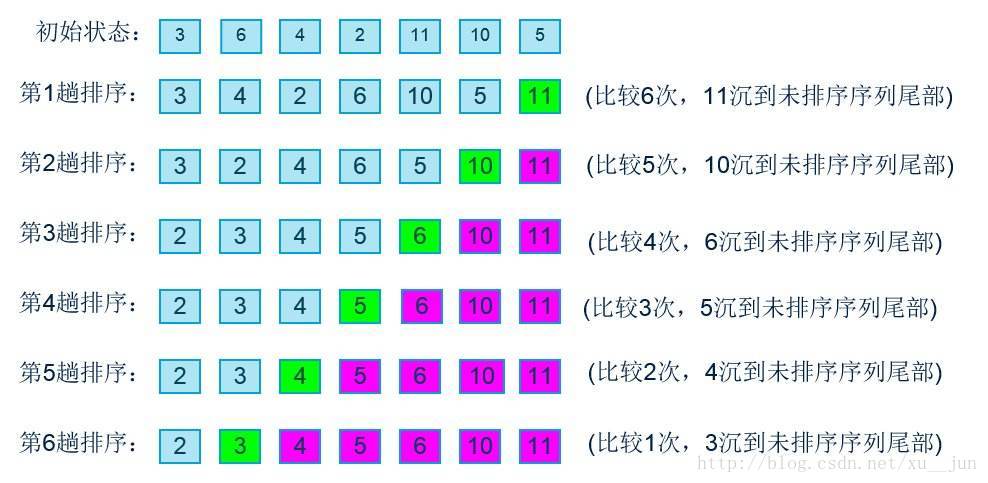
算法实现：

void bubbleSort(int arr[], int n)
{
    int i, j, tmp;

    for(i = 0; i < n - 1; i++)
    {
        for(j = 1; j < n; j++)
        {
            if(arr[j] < arr[j - 1])
            {
                tmp = arr[j];
                arr[j] = arr[j - 1];
                arr[j - 1] = tmp;
            }
        }
    }
}


void printArray(int arr[], int n)
{
    int i;
    for(i = 0; i < n; i++)
    {
        printf("%d ", arr[i]);
    }
    printf("\n");
}

void main()
{
    int arr[10] = {2,5,6,4,3,7,9,8,1,0};
    printArray(arr, 10);
    bubbleSort(arr, 10);
    printArray(arr, 10);
    return;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

如上是一种最简单的实现方式，需要注意的可能是i, j的边界问题，这种方式固定循环次数，肯定可以解决各种情况，不过算法的目的是为了提升效率，根据冒泡排序的过程图可以看出这个算法至少可以从两点进行优化：
1)对于外层循环，如果当前序列已经有序，即不再进行交换，应该不再进行接下来的循环直接跳出。
2)对于内层循环后面最大值已经有序的情况下应该不再进行循环。
优化代码实现：

void bubbleSort_1(int arr[], int n)
{
    int i, nflag, tmp;
    do
    {
        nflag = 0;
        for(i = 0; i < n - 1; i++)
        {
            if(arr[i] > arr[i + 1])
            {
                tmp = arr[i];
                arr[i] = arr[i + 1];
                arr[i + 1] = tmp;
                nflag = i + 1;
            }
        }
        n = nflag;
    }while(nflag);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

如上，当nflag为0时，说明本次循环没有发生交换，序列已经有序不用再循环，如果nflag>0则记录了最后一次发生交换的位置，该位置以后的序列都是有序的，循环不再往后进行。

---

3.插入排序-简单插入排序

插入排序是将一个记录插入到已经有序的序列中，得到一个新的元素加一的有序序列，实现上即将第一个元素看成一个有序的序列，从第二个元素开始逐个插入得到一个完整的有序序列，插入过程如下：

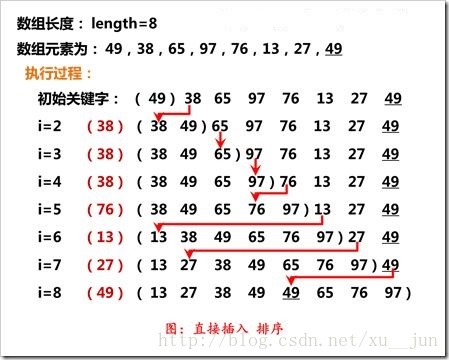
如图，插入排序第i个元素与相邻前一个元素比较，如果与排序顺序相反则与前一个元素交换位置，循环直到合适的位置。
算法实现：

void insertSort(int arr[], int n)
{
    int i, j, tmp;

    for(i = 1; i < n; i++)
    {
        for(j = i; j > 0; j--)
        {
            if(arr[j] < arr[j-1])
            {
                tmp = arr[j];
                arr[j] = arr[j-1];
                arr[j-1] = tmp;
            }
            else
            {
                break;
            }
        }
    }

    return;
}

void printArray(int arr[], int n)
{
    int i;
    for(i = 0; i < n; i++)
    {
        printf("%d ", arr[i]);
    }
    printf("\n");
    return;
}

void main()
{
    int arr[10] = {2,5,6,4,3,7,9,8,1,0};
    printArray(arr, 10);
    insertSort(arr, 10);
    printArray(arr, 10);
    return;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

如上，前面提到选择排序不管什么情况下都是固定为O(n2)的算法，插入算法虽然也是O(n2)的算法，不过可以看出，在已经有序的情况下，插入可以直接跳出循环，在极端情况下（完全有序）插入排序可以是O（n）的算法。不过在实际完全乱序的测试用例中，与本文中的选择排序相比，相同序列的情况下发现插入排序运行的时间比选择排序长，这是因为选择排序每次外循环只与选择的最值进行交换，而插入排序则需要不停与相邻元素交换知道合适的位置，交换的三次赋值操作同样影响运行时间，因此下面对这一点进行优化：
优化后实现：

void insertSort_1(int arr[], int n)
{
    int i, j, tmp, elem;

    for(i = 1; i < n; i++)
    {
        elem = arr[i];
        for(j = i; j > 0; j--)
        {
            if(elem < arr[j-1])
            {
                arr[j] = arr[j-1];
            }
            else
            {
                break;
            }
        }
        arr[j] = elem;
    }

    return;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

优化代码将需要插入的值缓存下来，将插入位置之后的元素向后移一位，将交换的三次赋值改为一次赋值，减少执行时间。

---

4.插入排序-希尔排序

希尔排序的基本思想是先取一个小于n的整数d1作为第一个增量，把全部元素分组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序；然后，取第二个增量d2 < d1重复上述的分组和排序，直至所取的增量 =1( < …< d2 < d1)，即所有记录放在同一组中进行直接插入排序为止，希尔排序主要是根据插入排序的一下两种性质对插入排序进行改进：
1)插入排序在对几乎已经排好序的数据操作时，效率高，即可以达到线性排序的效率。
2)但插入排序一般来说是低效的，因为插入排序每次只能将数据移动一位
排序过程如下：

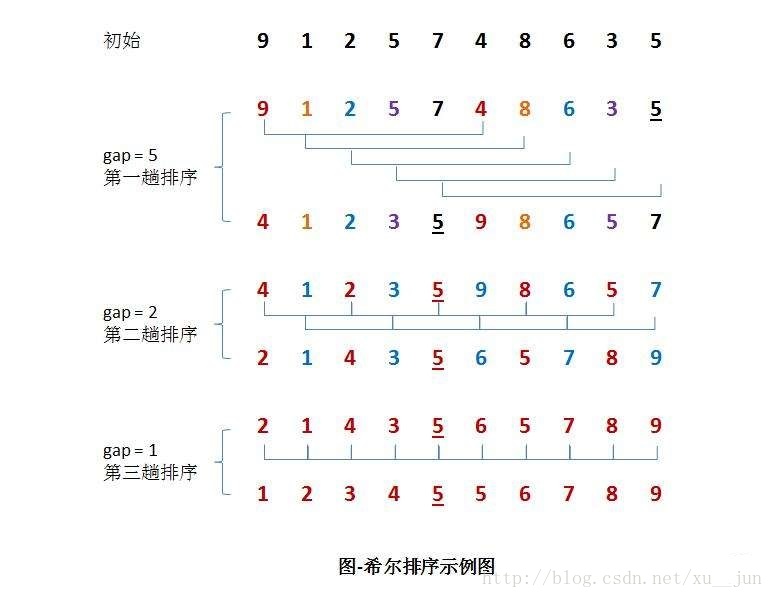
算法实现：基于一种简单的增量分组方式｛n/2,n/4,n/8……,1｝

void shellSort(int arr[], int n)
{
    int i, j, elem;
    int k = n/2;

    while(k>=1)
    {
        for(i = k; i < n; i ++)
        {
            elem = arr[i];
            for(j = i; j >= k; j-=k)
            {
                if(elem < arr[j-k])
                {
                    arr[j] = arr[j-k];
                }
                else
                {
                    break;
                }
            }
            arr[j] = elem;
        }
        k = k/2;
    }
}


void printArray(int arr[], int n)
{
    int i;
    for(i = 0; i < n; i++)
    {
        printf("%d ", arr[i]);
    }
    printf("\n");
    return;
}

void main()
{
    int arr[10] = {2,5,6,4,3,7,9,8,1,0};
    printArray(arr, 10);
    shellSort(arr, 10);
    printArray(arr, 10);
    return;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

5.归并排序

归并排序是基于归并操作的一种排序算法，归并操作的原理就是将一组有序的子序列合并成一个完整的有序序列，即首先需要把一个序列分成多个有序的子序列，通过分解到每个子序列只有一个元素时，每个子序列都是有序的，在通过归并各个子序列得到一个完整的序列。

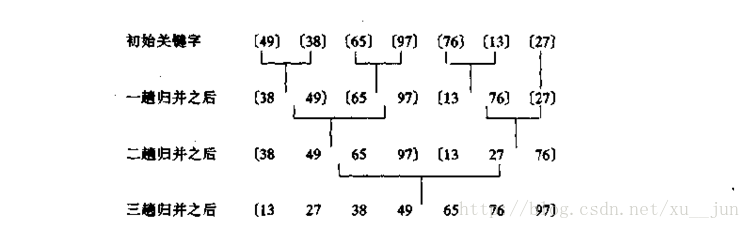
合并过程：
把序列中每个单独元素看作一个有序序列，每两个单独序列归并为一个具有两个元素的有序序列，每两个有两个元素的序列归并为一个四个元素的序列依次类推。两个序列归并为一个序列的方式：因为两个子序列都是有序的（假设由小到大），所有每个子序列最左边都是序列中最小的值，整个序列最小值只需要比较两个序列最左边的值，所以归并的过程不停取子序列最左边值中的最小值放到新的序列中，两个子序列值取完后就得到一个有序的完整序列。
归并的算法实现：

void merge(int arr[], int l, int mid, int r)
{
    int len,i, pl, pr;
    int *tmp = NULL;

    len = r - l + 1;
    tmp = (int*)malloc(len * sizeof(int));  //申请存放完整序列内存
    memset(tmp, 0x0, len * sizeof(int));

    pl = l;
    pr = mid + 1;
    i  = 0;
    while(pl <= mid && pr <= r)  //两个子序列都有值，比较最小值
    {
        if(arr[pl] < arr[pr])
        { 
            tmp[i++] = arr[pl++];
        }
        else
        {
            tmp[i++] = arr[pr++];
        }
    }
    while(pl <= mid)        //左边子序列还有值，直接拷贝到新序列中
    {
        tmp[i++] = arr[pl++];
    }
    while(pr <= r)      //右边子序列还有值
    {
        tmp[i++] = arr[pr++];
    }

    for(i = 0; i < len; i++)
    {
        arr[i+l] = tmp[i];
    }

    free(tmp);
    return;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

归并的迭代算法：
迭代算法如上面所说，从单个元素开始合并，子序列长度不停增加直到得到一个长度为n的完整序列。

#include<stdio.h>
#include<stdlib.h>
#include<string.h>

void merge(int arr[], int l, int mid, int r)
{
    int len,i, pl, pr;
    int *tmp = NULL;

    len = r - l + 1;
    tmp = (int*)malloc(len * sizeof(int));  //申请存放完整序列内存
    memset(tmp, 0x0, len * sizeof(int));

    pl = l;
    pr = mid + 1;
    i  = 0;
    while(pl <= mid && pr <= r)  //两个子序列都有值，比较最小值
    {
        if(arr[pl] < arr[pr])
        {

            tmp[i++] = arr[pl++];
        }
        else
        {
            tmp[i++] = arr[pr++];
        }
    }
    while(pl <= mid)        //左边子序列还有值，直接拷贝到新序列中
    {
        tmp[i++] = arr[pl++];
    }
    while(pr <= r)      //右边子序列还有值
    {
        tmp[i++] = arr[pr++];
    }

    for(i = 0; i < len; i++)
    {
        arr[i+l] = tmp[i];
    }

    free(tmp);
    return;

}
int min(int x, int y)
{
    return (x > y)? y : x;
}
/*
归并完成的条件是得到子序列长度等于n，用sz表示当前子序列的长度。从1开始每次翻倍直到等于n。根据上面归并的方法，从i=0开始分组，下一组坐标应该i + 2*sz，第i组第一个元素为arr[i],最右边元素应该为arr[i+2*sz -1]，遇到序列最右边元素不够分组的元素个数时应该取n-1,中间的元素为arr[i+sz -1],依次类推进行归并得到完整的序列
*/
void mergeSortBu(int arr[], int n)
{
    int sz, i, mid,l, r;
    for(sz = 1; sz < n; sz+=sz)
    {
        for(i = 0; i < n - sz; i += 2*sz)
        {
            l = i;
            r = i + sz + sz;
            mid = i + sz -1;
            merge(arr, l, mid, min(r-1, n-1));
        }
    }
    return;
}
void printArray(int arr[], int n)
{
    int i;
    for(i = 0; i < n; i++)
    {
        printf("%d ", arr[i]);
    }
    printf("\n");
    return;
}

void main()
{
    int arr[10] = {2,5,6,4,3,7,9,8,1,0};
    printArray(arr, 10);
    mergeSortBu(arr, 10);
    printArray(arr, 10);
    return;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88

另一种是通过递归的方式，递归方式可以理解为至顶向下的操作，即先将完整序列不停分解为子序列，然后在将子序列归并为完整序列。
递归算法实现：

void mergeSort(int arr[], int l, int r)
{
    if(l >= r)
    {
        return;
    }

    int mid = (l + r)/2;
    mergeSort(arr, l, mid);
    mergeSort(arr, mid+1, r);
    merge(arr, l, mid, r);
    return;
}
1
2
3
4
5
6
7
8
9
10
11
12
13

对于归并算法大家可以考虑到由于子序列都是有序的，所有如果左边序列的最大值都比右边序列的最小值小，那么整个序列就是有序的，不需要进行merge操作，因此可以在每次merge操作加一个if(arr[mid] > arr[mid+1])判断进行优化,这种优化对于近乎有序的序列非常有效果，不过对于一般的情况会有一次判断的额外开销，可以根据具体情况处理。

6.快速排序

快速排序跟归并排序类似属于分治法的一种，基本思想是通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。
排序过程如图：

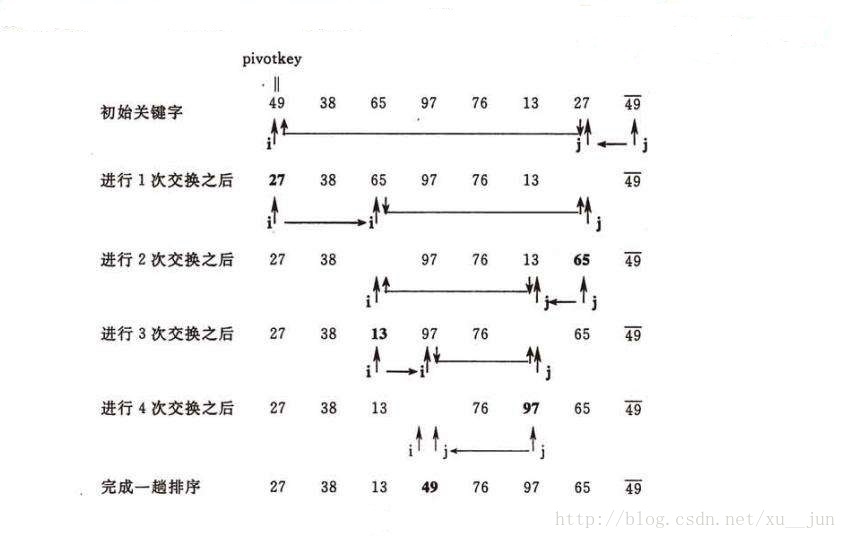
因此，快速排序每次排序将一个序列分为两部分，左边部分都小于等于右边部分，然后在递归对左右两部分进行快速排序直到每部分元素个数为1时则整个序列都是有序的，因此快速排序主要问题在怎样将一个序列分成两部分，其中一部分所有元素都小于另一部分，对于这一块操作我们叫做partition,原理是先选取序列中的一个元素做参考量，比它小的都放在序列左边，比它大的都放在序列右边。
算法实现：
快速排序-单路快排：

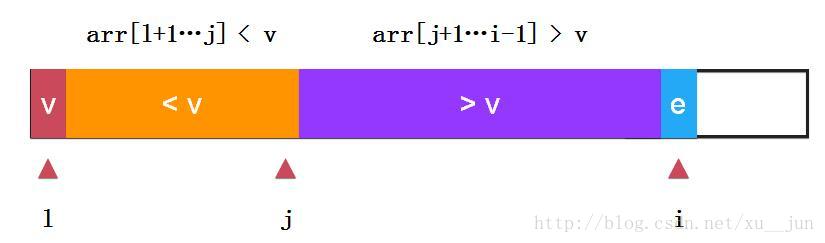
如上：我们选取第一个元素v作为参考量及arr[l],定义j变量为两部分分割哨兵，变量i从l+1开始遍历每个变量，如果当前变量e > v则i++检测下一个元素，如果当前变量e < v 则e与arr[j+1]交换，可以看到arr[j+1]由交换前大于v变成小于v arr[i]变成大于v，同时对i++，j++，始终保持：arr[l+1….j] < v, arr[j+1….i-1] > v
代码实现：

#include <stdio.h>

void printArray(int arr[], int n)
{
    int i;

    for(i = 0; i < n; i++)
    {
        printf("%d ", arr[i]);
    }
    printf("\n");
    return;
}
void swap(int *a, int *b)
{
    int tmp;

    tmp = *a;
    *a  = *b;
    *b  = tmp;
    return;
}
//arr[l+1...j] < arr[l], arr[j+1,..i)>arr[l]
static int partition(int arr[], int l, int r)
{
    int i, j;
    i = l + 1;
    j = l;

    while(i <= r)
    {
        if(arr[i] > arr[l])
        {
            i++;
        }
        else
        {
            swap(&arr[j + 1], &arr[i]);
            i++;
            j++;
        }
    }
    swap(&arr[l], &arr[j]);
    return j;
}

static void _quickSort(int arr[], int l, int r)
{
    int key;
    if(l >= r)
    {
        return;
    }
    key = partition(arr, l, r);
    _quickSort(arr, l, key - 1);
    _quickSort(arr, key + 1, r);
}

void quickSort(int arr[], int n)
{
    _quickSort(arr, 0, n - 1);
    return;
}

void main()
{
    int arr[10] = {1,5,9,8,7,6,3,4,0,2};

    printArray(arr, 10);
    quickSort(arr, 10);
    printArray(arr, 10);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73

因为有变量i从左到右依次遍历序列元素，所有这种方式叫单路快排，不过细心的同学可以发现我们忽略了考虑e等于v的情况，这种快排方式一大缺点就是对于高重复率的序列即大量e等于v的情况会退化为O（n2）算法，原因在大量e等于v的情况划分情况会如下图两种情况：

解决这种问题的一另种方法：
快速排序-两路快排：

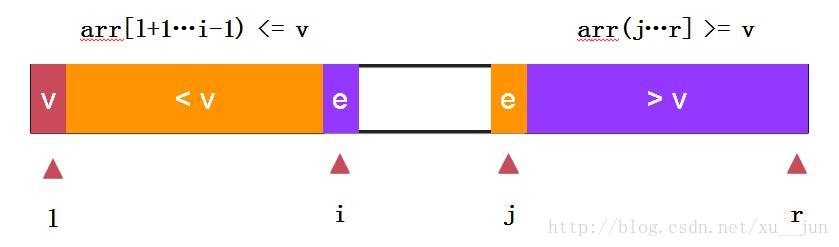
两路快排通过i和j同时向中间遍历元素，e==v的元素分布在左右两个部分，不至于在多重复元素时划分严重失衡。依旧去第一个元素arr[l]为参考量，始终保持arr[l+1….i) <= arr[l], arr(j…r] >=arr[l]原则.
代码实现：

//arr[l+1....i) <=arr[l], arr(j...r] >=arr[l]
static int partition2(int arr[], int l, int r)
{
    int i, j;

    i = l + 1 ;
    j = r;

    while(i <= j)
    {
        while(i <= j && arr[j] > arr[l])
         /*注意arr[j] >arr[l] 不是arr[j] >= arr[l]*/
        {
            j--;
        }
        while(i <= j && arr[i] < arr[l])
        {
            i++;
        }

        if(i < j)
        {
            swap(&arr[i], &arr[j]);
            i++;
            j--;
        }
    }
    swap(&arr[j],&arr[l]);
    return j;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

针对重复元素比较多的情况还有一种实现方式：
快速排序-三路快排：
三路快排是在两路快排的基础上对e==v的情况做单独的处理，对于重复元素非常多的情况优势很大：

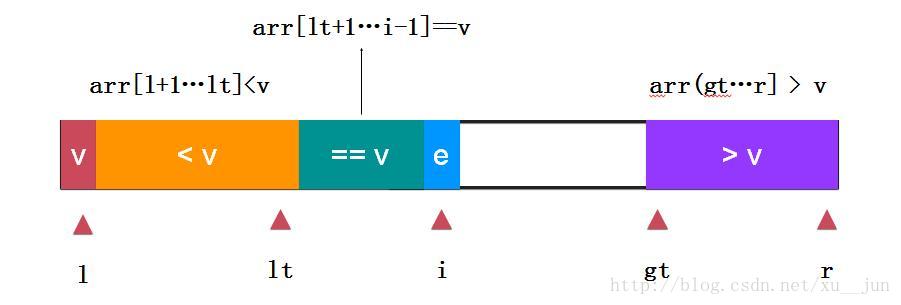
如上：取arr[l]为参考量，定义变量lt为小于v和等于v的分割点，变量i为遍历指针，gt为大于v和未遍历元素分割点，gt指向未遍历元素，边界条件跟个人定义有关本文始终保持arr[l+1…lt] < v,arr[lt+1….i-1],arr(gt…..r]>v的状态。
代码实现：

#include <stdio.h>

void printArray(int arr[], int n)
{
    int i;

    for(i = 0; i < n; i++)
    {
        printf("%d ", arr[i]);
    }
    printf("\n");
    return;
}
void swap(int *a, int *b)
{
    int tmp;

    tmp = *a;
    *a  = *b;
    *b  = tmp;
    return;
}

static void _quickSort3(int arr [ ],int l,int r)
{
    int i, lt, gt;

    if(l >= r)
    {
        return;
    }
    i = l + 1;
    lt = l;
    gt = r ;

    while(i <= gt)
    {
        if(arr[i] < arr[l])
        {
            swap(&arr[lt + 1], &arr[i]);
            lt ++;
            i++;
        }
        else if(arr[i] > arr[l])
        {
            swap(&arr[i], &arr[gt]);
            gt--;
        }
        else
        {
            i++;
        }
    }

    swap(&arr[l], &arr[gt]);
    _quickSort3(arr, l, lt);
    _quickSort3(arr, gt + 1, r);
    return;
}

void quickSort(int arr[], int n)
{
    _quickSort3(arr, 0, n - 1);
    return;
}

void main()
{
    int arr[10] = {1,5,9,8,7,6,3,4,0,2};

    printArray(arr, 10);
    quickSort(arr, 10);
    printArray(arr, 10);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75

三路快排在重复率比较高的情况下比前两种有较大优势，但就完全随机情况略差于两路快排，可以根据具体情况进行合理选择，另外本文在选取参考值时为了方便一直选择第一个元素为参考值，这种方式对于近乎有序的序列算法会退化到O（n2），因此一般选取参考值可以随机选择参考值或者其他选择参考值的方法然后再与arr[l]交换，依旧可以使用相同的算法。

7.堆排序

堆其实一种树形结构，以二叉堆为例，是一颗完全二叉树（即除最后一层外每个节点都有两个子节点，且非满的二叉树叶节点都在最后一层的左边位置），二叉树满足每个节点都大于等于他的子节点(大顶堆)或者每个节点都小于等于他的子节点（小顶堆），根据堆的定义可以得到堆满足顶点一定是整个序列的最大值（大顶堆）或者最小值（小顶堆）。如下图：

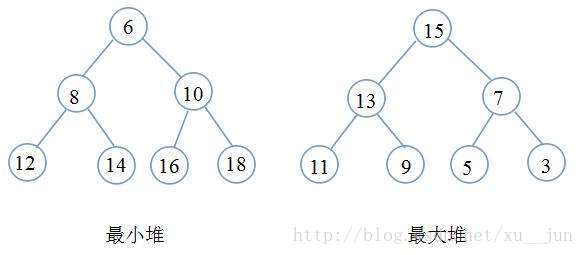
堆排序就是一种基于堆得选择排序，先将需要排序的序列构建成堆，在每次选取堆顶点的最大值和最小值知道完成整个堆的遍历。
用数组表示堆：
二叉堆作为树的一种，通常用结构体表示，为了排序的方便，我们通常使用数组来表示堆，如下图：

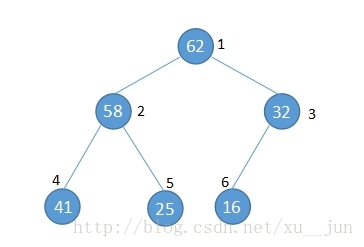
将一个堆按图中的方式按层编号可以得到如下结论：
1）节点的父节点编号满足parent(i) = i/2
2）节点的左孩子编号满足 left child (i) = 2*i
3）节点右孩子满足 right child (i) = 2*i + 1
由于数组编号是从0开始对上面结论修改得到：
parent(i) = (i-1)/2
left child (i) = 2*i + 1
right child (i) = 2*i + 2
堆的两种操作方式：
根据堆的主要性质（父节点大于两个子节点或者小于两个子节点），可以得到堆的两种主要操作方式，以大顶堆为例：
a）如果子节点大于父节点将子节点上移（shift up）
b）如果父节点小于两个子节点中的最大值则父节点下移（shift down）
shift up:
如果往已经建好的堆中添加一个元素，如下图，此时不再满足堆的性质，堆遭到破坏，就需要执行shift up 操作将添加的元素上移调整直到满足堆的性质。

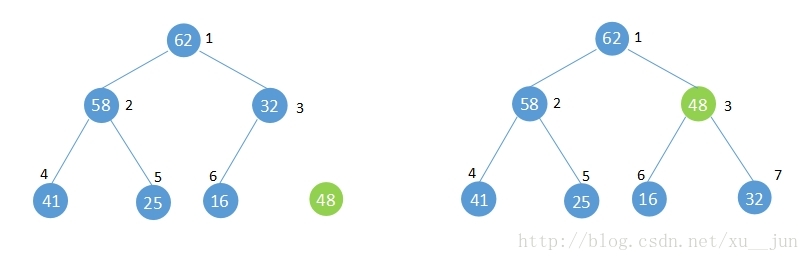
调整堆的方法：
1）7号位新增元素48与其父节点[i/2]=3比较大于父节点的32不满足堆性质，将其与父节点交换。
2）此时新增元素在3号位，再与3号位父节点[i/2]=1比较，小于1号位的62满足堆性质，不再交换，如果此步骤依旧不满足堆性质则重复1步骤直到满足堆的性质或者到根节点。
3）堆调整完成。
代码实现：
代码中基于数组实现，数组下表从0开始，父子节点关系如用数组表示堆

/*parent(i) = (i-1)/2
  left child  (i) = 2*i + 1
  right child (i) = 2*i + 2
*/

void swap(int *a, int *b)
{
    int tmp;

    tmp = *a;
    *a  = *b;
    *b  = tmp;
    return;
}

 void shiftUp(int arr[], int n, int k)
 {
    while((k - 1)/2 >= 0 && arr[k] > arr[(k - 1)/2])
    {
        swap(&arr[k], &arr[(k-1)/2]);
        k = (k - 1)/2;
    }
    return;
 }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

shift down:
与shift up相反，如果从一个建好的堆中删除一个元素，此时不再满足堆的性质，此时应该怎样来调整堆呢？

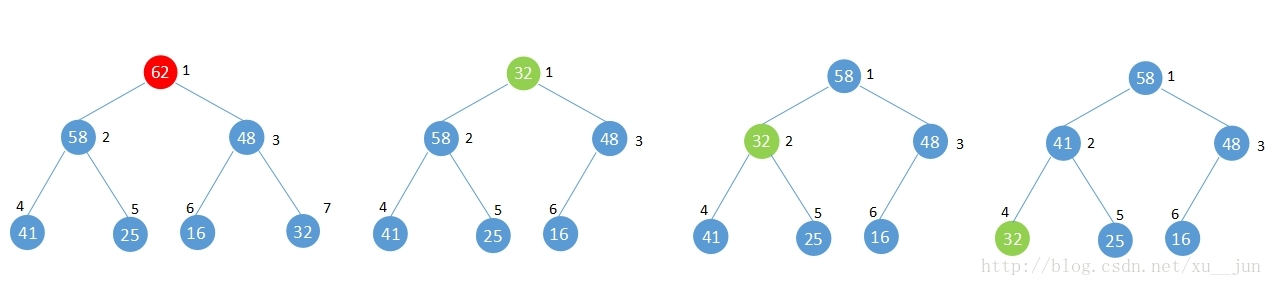
如上图，将堆中根节点元素62删除调整堆的步骤为：
1）将最后一个元素移到删除节点的位置
2）与删除节点两个子节点中较大的子节点比较，如果节点小于较大的子节点，与子节点交换，否则满足堆性质，完成调整。
3）重复步骤2，直到满足堆性质或者已经为叶节点。
4）完成堆调整
代码实现：

 void shiftDown(int arr[], int n, int k)
 {
    int j = 0 ;

     while(2*k + 1 < n)
     {
        j = 2 *k + 1;    //标记两个子节点较大的节点，初始为左节点
        if (j + 1 < n && arr[j] < arr[j+1])
        {
            j ++;   
        }

        if(arr[k] < arr[j])
        {
            swap(&arr[k], &arr[j]);
            k = j;
        }
        else
        {
            break;
        }
     }

     return;
 }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

知道了上面两种堆的操作后，堆排序的过程就非常简单了
1）首先将待排序序列建成堆，由于最后一层即叶节点没有子节点所以可以看成满足堆性质的节点，第一个可能出现不满足堆性质的节点在第一个父节点的位置，假设最后一个叶子节点为（n - 1） 则第一个父节点位置为(n-1-1)/2,只需要依次对第一个父节点之前的节点执行shift down操作到根节点后建堆完成。
2）建堆完成后（以大顶堆为例）第一个元素arr[0]必定为序列中最大值，将最大值提取出来（与数组最后一个元素交换），此时堆不再满足堆性质，再对根节点进行shift down操作，依次循环直到根节点，排序完成。
代码实现：

#include<stdio.h>

/*parent(i) = (i-1)/2
  left child  (i) = 2*i + 1
  right child (i) = 2*i + 2
*/

void swap(int *a, int *b)
{
    int tmp;

    tmp = *a;
    *a  = *b;
    *b  = tmp;
    return;
}

 void shiftUp(int arr[], int n, int k)
 {
    while((k - 1)/2 >= 0 && arr[k] > arr[(k - 1)/2])
    {
        swap(&arr[k], &arr[(k-1)/2]);
        k = (k - 1)/2;
    }
    return;
 }

 void shiftDown(int arr[], int n, int k)
 {
    int j = 0 ;

     while(2*k + 1 < n)
     {
        j = 2 *k + 1;
        if (j + 1 < n && arr[j] < arr[j+1])
        {
            j ++;   
        }

        if(arr[k] < arr[j])
        {
            swap(&arr[k], &arr[j]);
            k = j;
        }
        else
        {
            break;
        }
     }

     return;
 }

 void heapSort(int arr[], int n)
 {
    int i = 0;
    for(i = (n - 1 -1)/2; i >=0; i--)
    {
        shiftDown(arr, n, i);
    }

    for(i = n - 1; i > 0; i--)
    {
        swap(&arr[0], &arr[i]);
        shiftDown(arr, i, 0);
    }
    return;
 }

 void printArray(int arr[], int n)
{
    int i;

    for(i = 0; i < n; i++)
    {
        printf("%d ", arr[i]);
    }
    printf("\n");
    return;
}
 void main()
{
    int arr[10] = {1,5,9,8,7,6,3,4,0,2};

    printArray(arr, 10);
    heapSort(arr, 10);
    printArray(arr, 10);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88

总结

待续……..