- 1网络通信的隐形桥梁:深入解析地址解析协议(ARP)及其在现代网络安全中的角色
- 2初学者专题:KALI的安装_怎么下载kali
- 3技术写作,如何从日赚0.1元到日赚100元,内含CSDN专栏推广秘籍【赢在CSDN】_csdn如何获取收益
- 4stm32毕业设计 单片机智能手环_基于stm32的智能手表的设计与实现 1.采用stm32微控制器。2.采用mpu6050实现姿态解
- 5nRF52832 — ANCS协议介绍
- 6(YOLOv5-lite)-ONNX模型转换及Openvino推理_v5lite-s.pt 下载
- 7python金融分析小知识(13)——Jupyter Notebook中一行代码实现页面源代码的获取_jupyter怎么查看保存的网页源代码
- 8特征工程——文本特征_文本特征工程
- 9css控制元素像素计算方式
- 10pygame之draw模块_pygame draw rect
MATLAB2016笔记(五):进阶矩阵操作_希尔伯特矩阵的奇异值
赞
踩
一、特殊矩阵创建
(一)希尔伯特矩阵 hilb()
希尔伯特(Hilbert)矩阵,也叫 H H H阵,其元素为 H i j = 1 i + j − 1 H_{ij}=\frac{1}{i+j-1} Hij=i+j−11
由于它是一个条件数差的矩阵,所以可以将它用作实验矩阵
关于希尔伯特矩阵的指令函数如下:
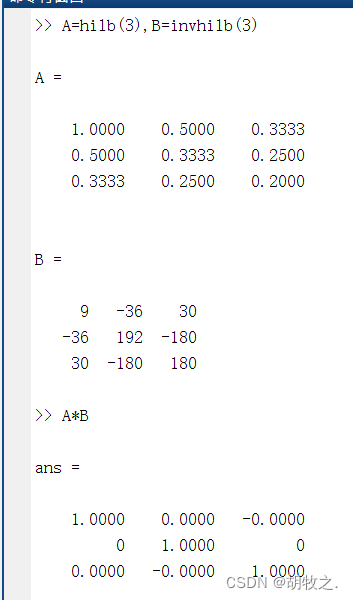
1. hilb(n) 用于生成一个n*n的希尔伯特矩阵
2. invhilb(n) 用于生成一个n*n的希尔伯特矩阵的逆矩阵(整数矩阵)
- 1
- 2
- 3
- 4
- 5
- 6
(二)托普利兹矩阵 toeplitz()
托普利兹(Toeplitz)矩阵,它的主对角线上的元素相等,平行于主对角线的线上的元素也相等;矩阵中的各元素关于次对角线对称
关于托普利兹矩阵的指令函数如下:
1.toeplitz(k,r) 用于生成非对称托普利兹矩阵,k为第一列,r为第一行,k与r为长度不一定相等的向量
所得矩阵中其余的元素等于各自左上角元素
注意行列向量的首位元素要相同
2.toeplitz(c) 用于用向量c生成一对称的托普利兹矩阵
- 1
- 2
- 3
- 4
- 5

(三)0~1间均匀分布的随机矩阵 rand()
通过rand()函数产生0~1间均匀分布的随机矩阵


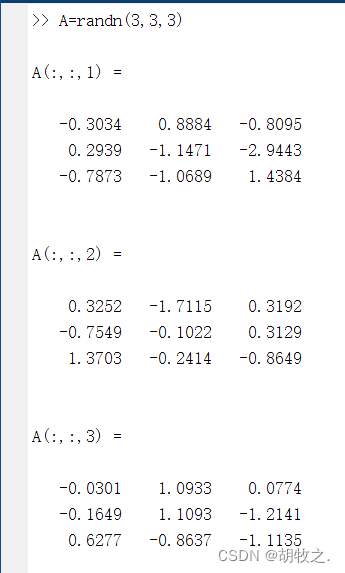
(四)标准正态分布随机矩阵 randn()
通过randn()函数产生均值为0、方差为1的随机矩阵
调用方法与rand()类似
- 1
(五)魔方矩阵 magic()
魔方矩阵中每行、每列和两条对角线上的元素和相等,调用形式如下:
M=magic(n)
- 1

(六)帕斯卡矩阵 pascal()
帕斯卡矩阵,由杨辉三角形表组成,除首行首列外,每个元素为左侧元素与上侧元素之和
其调用形式如下:
1.A=pascal(n) 返回n阶的对称正定Pascal矩阵,元素均为整数
2.A=pascal(n,1) 返回由下三角的Cholesky因子组成的Pascal矩阵,由于它本身对称,所以它是自己的逆
3.A=pascal(n,2) 返回pascal(n,1)的转置和交换形式,A是单位矩阵的立方根
- 1
- 2
- 3

(七)范德蒙矩阵 vander()
范德蒙矩阵的第
i
i
i行
j
j
j列表示为
a
i
j
−
1
a_i^{j-1}
aij−1
A
=
[
1
a
1
2
.
.
.
a
1
n
−
1
1
a
2
2
.
.
.
a
2
n
−
1
⋮
⋮
⋮
1
a
m
2
.
.
.
a
m
n
−
1
]
A=\left[
其调用形式如下:
A=vander(v) v是向量,矩阵的列是向量v的幂,矩阵列数等于v的长度
- 1

二、改变矩阵大小
(一)矩阵合并
矩阵合并就是把两个或者两个以上的矩阵数据连接起来得到一个新的矩阵
使用“ [] ”实现水平方向合并与竖直方向合并
需要注意的是要保证合并前后矩阵为方形,否则矩阵合并无法进行
- 1
- 2
- 3

(二)矩阵行列删除
要删除矩阵的某一行或某一列,只要把该行或该列赋予一个空矩阵即可

三、矩阵重构
(一)位置转置 A . ′ A_{.}^{'} A.′
只对位置进行改变,即便元素是复数也不受影响
- 1

(二)共轭转置 A ′ A^{'} A′
对于实数矩阵,共轭转置的结果不变
对于复数矩阵,共轭转置后不仅位置变化,元素也是共轭的
- 1
- 2

四、矩阵元素运算
(一)矩阵加减
矩阵之间必须具有相同的维数
标量则作用于对应矩阵的所有元素
- 1
- 2
(二)矩阵乘法
矩阵间乘法满足被乘矩阵的列数与乘矩阵的行数相等,不遵循交换律
标量则作用于对应矩阵的所有元素
- 1
- 2
(三)矩阵除法
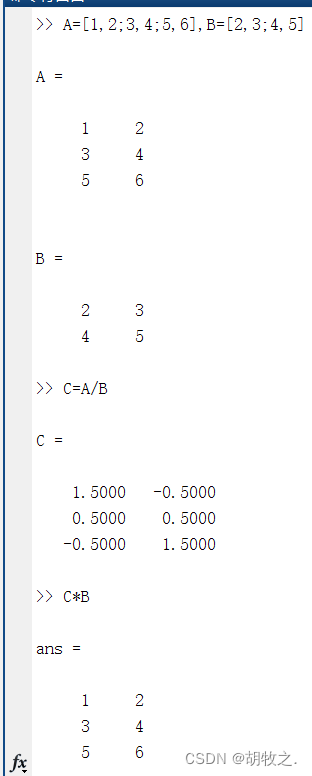
矩阵除法是乘法的逆运算,分为左除(\)和右除(/)两种
数组间乘除要求维数相同
右除(/)为一般意义的除法,与左除关系如下:
A/B=B\A
- 1
对于一般的二维矩阵 A A A和 B B B:
当进行A\B运算时,要求A的行数与B的行数相等
当进行A/B运算时,要求A的列数和B的列数相等
- 1
- 2
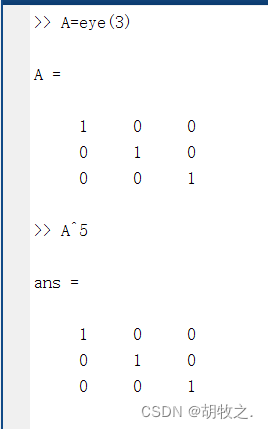
(四)矩阵幂运算
当矩阵
A
A
A为方阵时,可以进行矩阵的幂运算,其定义为:
C
=
A
n
=
A
×
A
×
.
.
.
×
A
⏟
n
C=A^{n}=\underbrace{A \times A \times ... \times A}_n
C=An=n
A×A×...×A
在
M
A
T
L
A
B
MATLAB
MATLAB中,使用运算符号“ ^ ”表示幂运算
五、矩阵元素操作
(一)元素查找 find()
函数find()的作用是进行矩阵元素的查找,它通常与关系函数和逻辑运算相结合
其语法格式如下:
ind = find(X) 查找矩阵X中的非零元素,函数返回这些元素的单下标
[row,col] = find(X,...) 查找矩阵X中的非零元素,函数返回这些元素的双下标
可在圆括号内添加限定条件
- 1
- 2
- 3
- 4
- 5
- 6
- 7
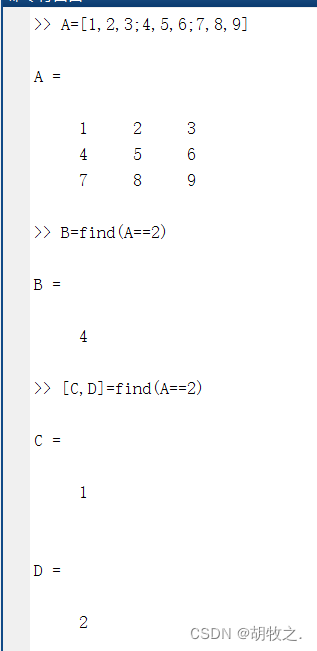
(二)元素排序 sort()
函数sort()的作用是按照升序排列,排序后的矩阵和原矩阵的维数相同
其语法格式如下:
sort(A,dim) dim默认为1,仅对列进行排序;dim为2时,对行进行排序
sort(...,mode) mode可以指定排序的方式,默认为ascend升序;descend,指定降序排列
- 1
- 2
- 3
- 4
- 5
- 6
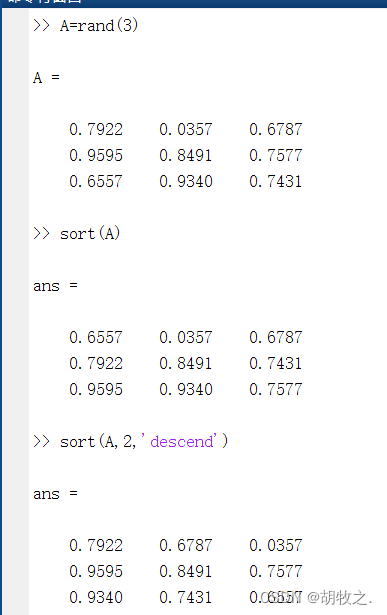
(三)元素求和 sum() cumsum()
函数sum()和cumsum()的作用是对矩阵的元素求和
其语法格式如下:
sum(A,dim) 返回由和所组成的向量,dim默认为1,计算矩阵A各列元素的和;dim=2时,计算矩阵A各行元素的和
cumsum(A,dim) 返回一个前缀和矩阵,dim默认为1,计算矩阵A各列元素的和;dim=2时,计算矩阵A各行元素的和
通过sum(sum(A))就可以求出A中所有矩阵元素之和
- 1
- 2
- 3
- 4
- 5
- 6
- 7
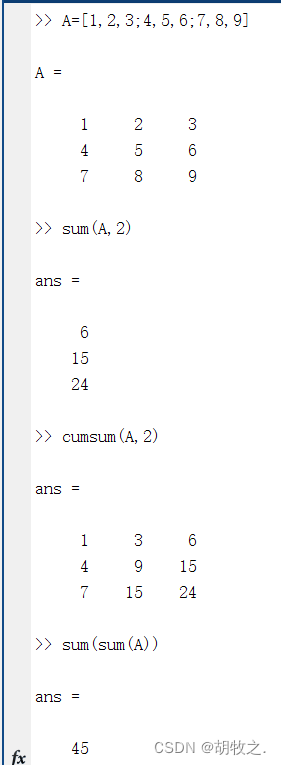
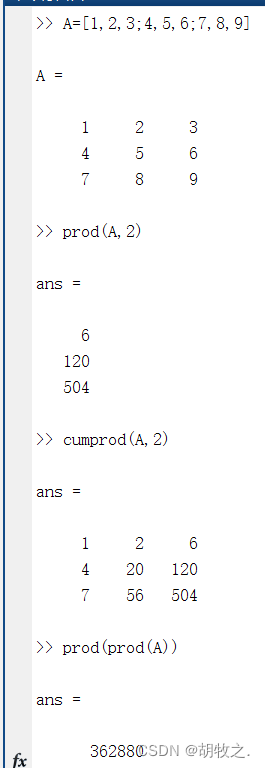
(四)元素求积 prod() cumprod()
函数prod()和cumprod()的作用是对矩阵的元素求积
其语法格式如下:
prod(A,dim) 返回由积所组成的向量,dim默认为1,计算矩阵A各列元素的积;dim=2时,计算矩阵A各行元素的积
cumprod(A,dim) 返回一个前缀积矩阵,dim默认为1,计算矩阵A各列元素的积;dim=2时,计算矩阵A各行元素的积
同理,同样可以通过prod(prod(A))求出A中所有矩阵元素之积
- 1
- 2
- 3
- 4
- 5
- 6
- 7
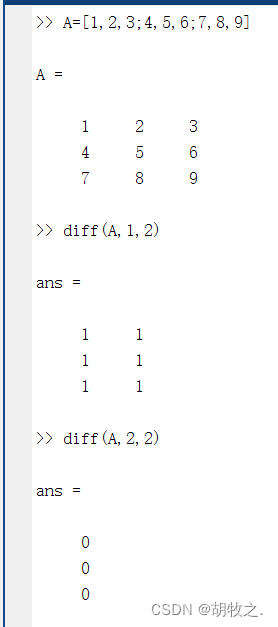
(五)元素差分 diff()
函数diff()的作用是计算矩阵的差分
其语法格式如下:
diff(A,n,dim) X为矩阵,n表示计算结果是n阶差分,默认为1;dim默认为1,计算各列差分;dim为2,计算各行差分
首行或首列没有差分值,所以所得矩阵会少一行或一列
当n>size(X,dim),函数返回值是空矩阵
- 1
- 2
- 3
- 4
- 5
- 6
- 7
六、矩阵分析
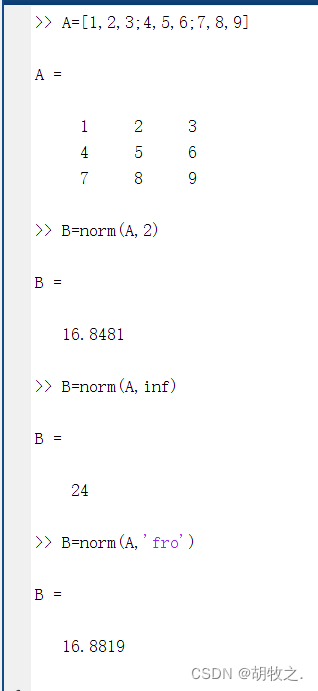
(一)向量和矩阵的范数运算(定义、计算)norm()
1.求向量范数的函数:
- 1


2.求矩阵范数的函数:
勘误,下方求F范数,参数应为:“fro”
当矩阵维数较大时,会导致计算矩阵范数的时间比较长
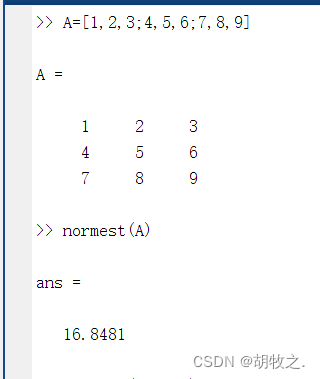
并且当一个近似的范数值可以满足要求时,可以考虑使用函数normest()来估计2阶范数值
normest()最初开发是为了提供给稀疏矩阵,同时它可以接收满矩阵的输入,一般在满矩阵维数较大时使用
其用法如下:
normest(S) 估计矩阵S的2阶范数值
normest(S,tol) 估计矩阵S的2阶范数值,使用tol作为允许的相对误差
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11

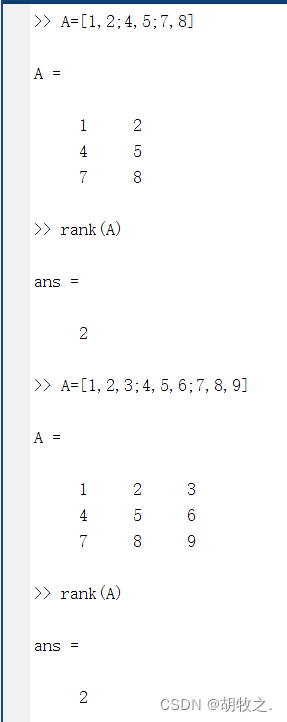
(二)矩阵的秩 rank()
矩阵中线性无关的列向量个数称为列秩,线性无关的行向量个数为行秩
方阵(行数、列数相等的矩阵)的列秩和行秩总是相等的,因此它们可以简单地称作矩阵A的秩
m×n矩阵的秩最大为m和n中的较小者,表示为 min(m,n)。有尽可能大的秩的矩阵被称为有满秩;类似的,否则矩阵是秩不足(或称为“欠秩”)的
函数rank()用于计算矩阵的秩,用法如下:
rank(A) 用默认允许误差计算矩阵的秩
rank(A,tol) 给定允许误差计算矩阵的秩
tol = max(size(A) * eps(norm(A)))
- 1
- 2
- 3
- 4
- 5
(三)矩阵的行列式 det()
矩阵
A
=
{
a
i
j
}
n
×
n
A=\{a_{ij}\}_{n \times n}
A={aij}n×n的行列式定义:
∣
∣
A
∣
∣
=
d
e
t
(
A
)
=
∑
k
=
1
n
(
−
1
)
k
a
1
k
1
a
2
k
2
.
.
.
a
n
k
n
|| A||=det(A)=\sum_{k=1}^{n}(-1)^{k}a_1k_1a_2k_2...a_nk_n
∣∣A∣∣=det(A)=∑k=1n(−1)ka1k1a2k2...ankn
其中,
k
1
,
k
2
,
.
.
.
,
k
n
k_1,k_2,...,k_n
k1,k2,...,kn是将序列
1
,
2
,
.
.
.
,
n
1,2,...,n
1,2,...,n交换
k
k
k次所得的序列
一个n×n矩阵的行列式等于其任意行(或列)的元素与对应的代数余子式乘积之和,即 d e t ( A ) = a i 1 A i 1 + . . . + a i n A i n = ∑ j = 1 n a i j ( − 1 ) i + j M i j det(A)=a_{i1}A_{i1}+...+a_{in}A_{in}=\sum_{j=1}^{n}a_{ij}(-1)^{i+j}M_{ij} det(A)=ai1Ai1+...+ainAin=∑j=1naij(−1)i+jMij
函数det()用于计算矩阵的行列式
- 1
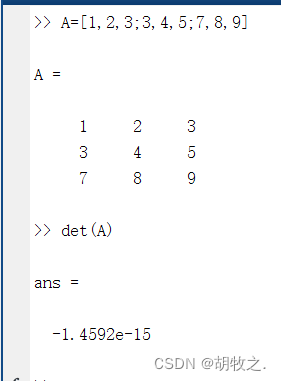
(四)矩阵的迹 trace()
在线性代数中,一个n×n矩阵A的主对角线(从左上方至右下方的对角线)上各个元素的总和被称为矩阵A的迹(或迹数),一般记作tr(A)
函数trace()用于计算矩阵的迹
- 1
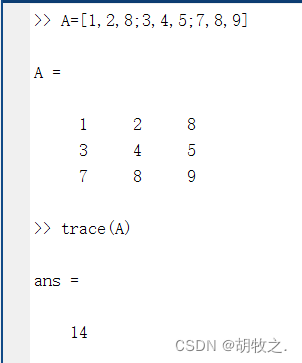
(五)矩阵的化零矩阵 null()
对于非满秩矩阵 A A A,若存在矩阵 B B B使 A × B = 0 A\times B=0 A×B=0,且 B × B = I B\times B=I B×B=I,即不等于 0 0 0,则称矩阵 B B B为矩阵 A A A的化零矩阵
函数null()可以用于求解化零矩阵,其用法格式如下:
null(A) 返回矩阵A的一个化零矩阵,若化零矩阵不存在则返回空矩阵
null(A,'r') 返回有理数形式的化零矩阵
- 1
- 2
- 3
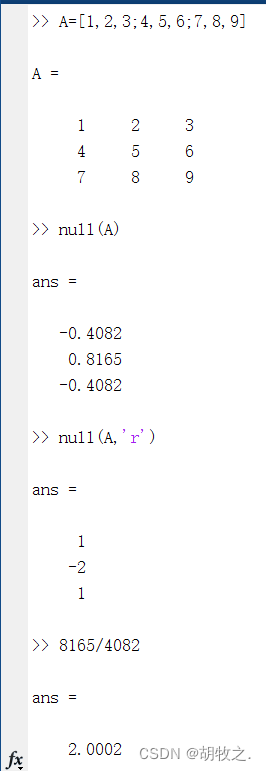
(六)矩阵的正交空间 orth()
矩阵 A A A的正交空间 Q Q Q具有 Q ′ × Q = I Q^{'} \times Q=I Q′×Q=I的性质,并且 Q Q Q的列矢量构成的线性空间与矩阵 A A A的列矢量构成的线性空间相同,且正交空间 Q Q Q与矩阵 A A A具有相同的秩
函数otrh()可以用于求解正交空间
- 1
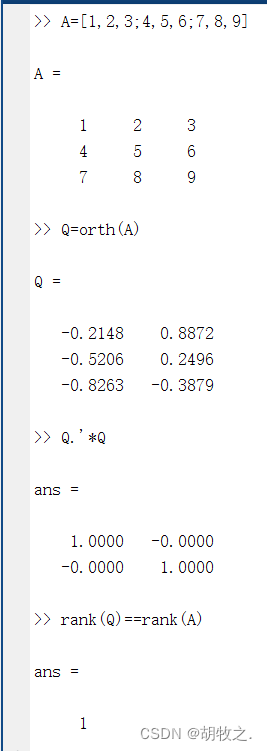
(七)矩阵的约化行阶梯形式 rref()
矩阵的约化行列阶梯形式是高斯-约旦消去法解线性方程组的结果
函数rref()可以用于求矩阵的约化行阶梯形式,其用法如下:
R = rref(A) 返回A的约化行阶梯形式R
[R,jb] = rref(A) jb为1*r的向量,r为矩阵A的秩
A(:,jb)是矩阵A的列矢量构成的线性空间;
R(1:r,jb)是r*r的单位矩阵
[R,jb] = rref(A,tol) 以tol作为允许的相对误差计算矩阵A的秩
- 1
- 2
- 3
- 4
- 5
- 6

(八)矩阵空间之间的夹角 subspace()
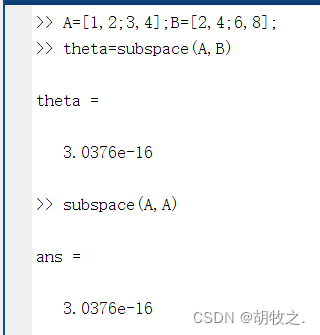
矩阵空间之间的夹角代表两个矩阵线性相关的程度,如果夹角很小,它们之间的线性相关度就很高,反之,它们之间的线性相关度就不大
函数subspace()可以求出矩阵空间之间的夹角,其用法如下:
theta = subspace(A,B) 返回矩阵A和矩阵B之间的夹角
- 1
- 2
七、矩阵分解
矩阵分解是把一个矩阵分解为几个“较简单”的矩阵连乘的形式
知乎——矩阵分解
百度——矩阵分解
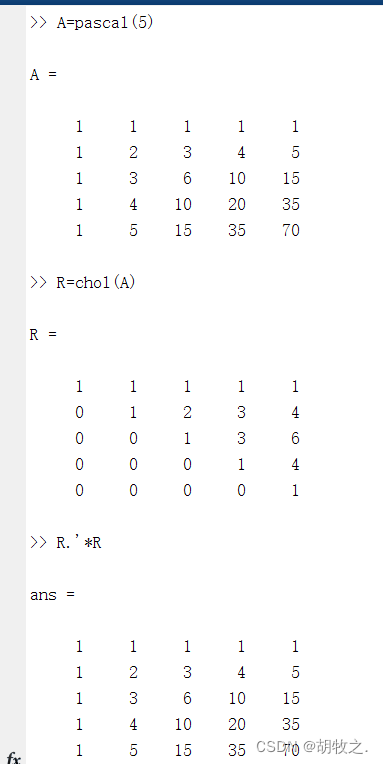
(一)对称正定矩阵的Cholesky分解 chol()

函数chol()可以实现Cholesky分解,其常用调用方法如下:
R = chol(X) X为对称正定矩阵,R为上三角矩阵,使得X=R'*R,如果X是非正定的,将报错
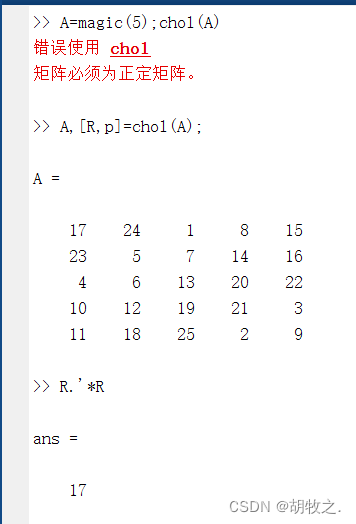
[R,p] = chol(X) 当X为正定矩阵,返回的上三角矩阵R满足X=R'*R,且p=0;若X是非正定矩阵,R阶数为p-1,且满足X(1:p-1,1:p-1)=R'*R
- 1
- 2
- 3
- 4
(二)稀疏矩阵的不完全Cholesky分解 cholinc()/ichol()
函数cholinc()用于对稀疏矩阵进行不完全的Cholesky分解,还可以用于计算实半正定矩阵,其调用格式如下:
R = cholinc(X,DROPTOL) 其中X与R的含义与chol()中相同,DROPTOL为不完全Cholesky分解的丢失容限
当DROPTOL为'0',该函数作用就是完全Cholesky分解
当DROPTOL为'inf',该函数采用Cholesky-Infinity分解,可以处理实半正定矩阵
R = cholinc(X,OPTS) 其中OPTS为结构体,含有三个属性,分别为DROPTOL、MICHOL和RDIAG
DROPTOL 与上方含义相同
MICHOL 该值为1时采用改进算法的不完全Cholesky分解,否则不采用
RDIAG 该值为1时R的对角元素中的零值替换为DROPTOL的平方根,为0时不做替换
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
但在2013版后,MATLAB中就没有cholinc()了,只有ichol()有类似的功能
而参数opts为结构体
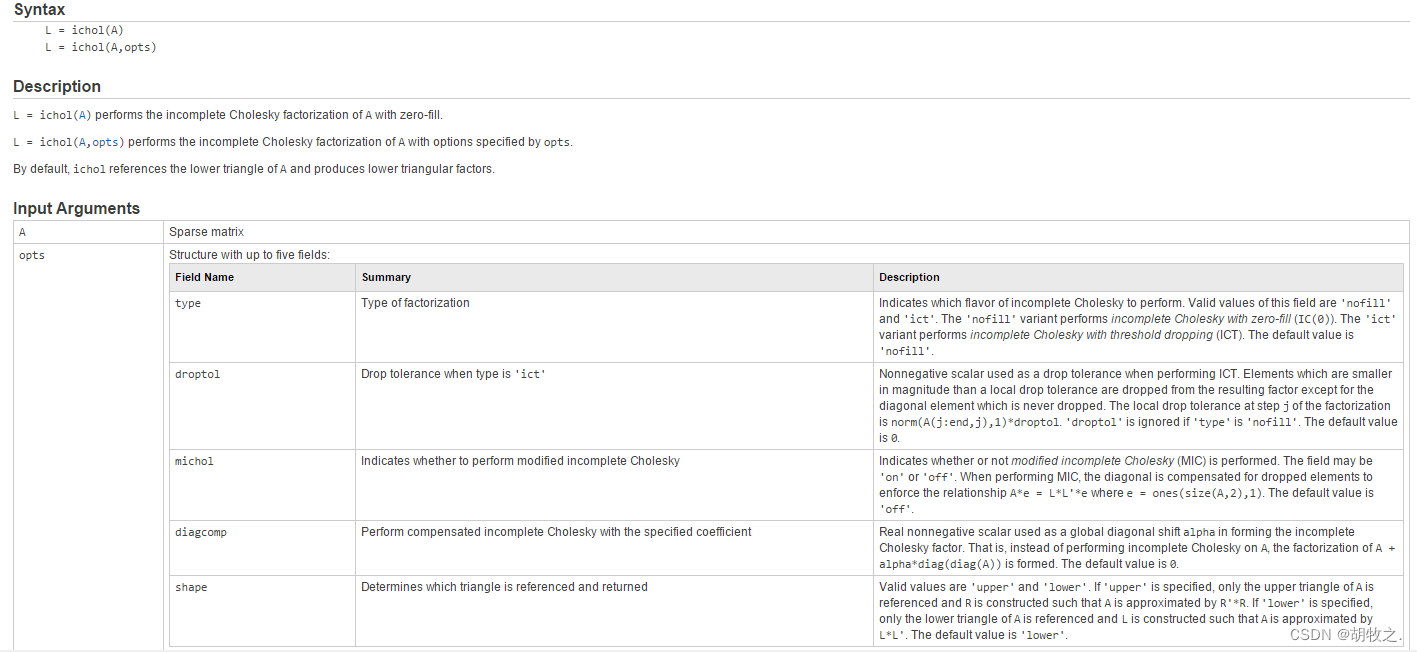
(三)一般方阵的高斯消去法分解(LU分解) lu()
高斯消去法分解又称为 L U LU LU分解,它可以将任意一个方阵 A A A分解为一个下三角矩阵 L L L和一个上三角矩阵 U U U的乘积,即 A = L U A=LU A=LU
函数lu()可以实现LU分解,其调用形式如下:
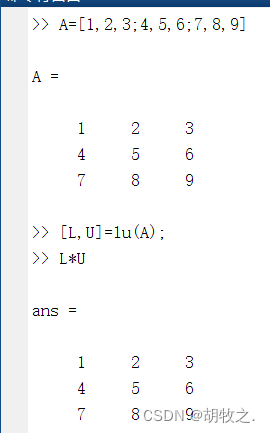
[L,U]=lu(X) X为一个方阵,L为下三角矩阵,U为上三角矩阵,满足:X=L*U
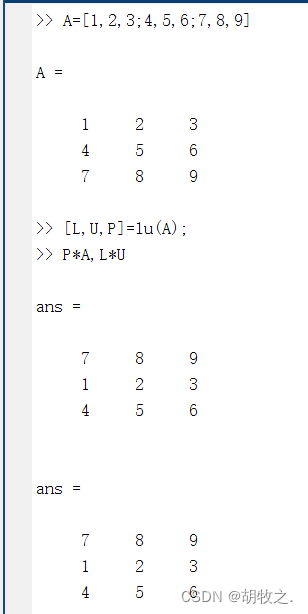
[L,U,P]=lu(X) X为一个方阵,L为下三角矩阵,U为上三角矩阵,P为置换矩阵,满足:P*X=L*U
Y=lu(X) L与U合并在矩阵Y中,矩阵Y的对角元素为上三角矩阵(U)的对角元素,即Y=L+U-I (//尚未实践证明)
利用LU分解来计算行列式的值和矩阵的逆,其命令形式如下:
det(A)=det(L)*det(U)
inv(A)=inv(U)*inv(L)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
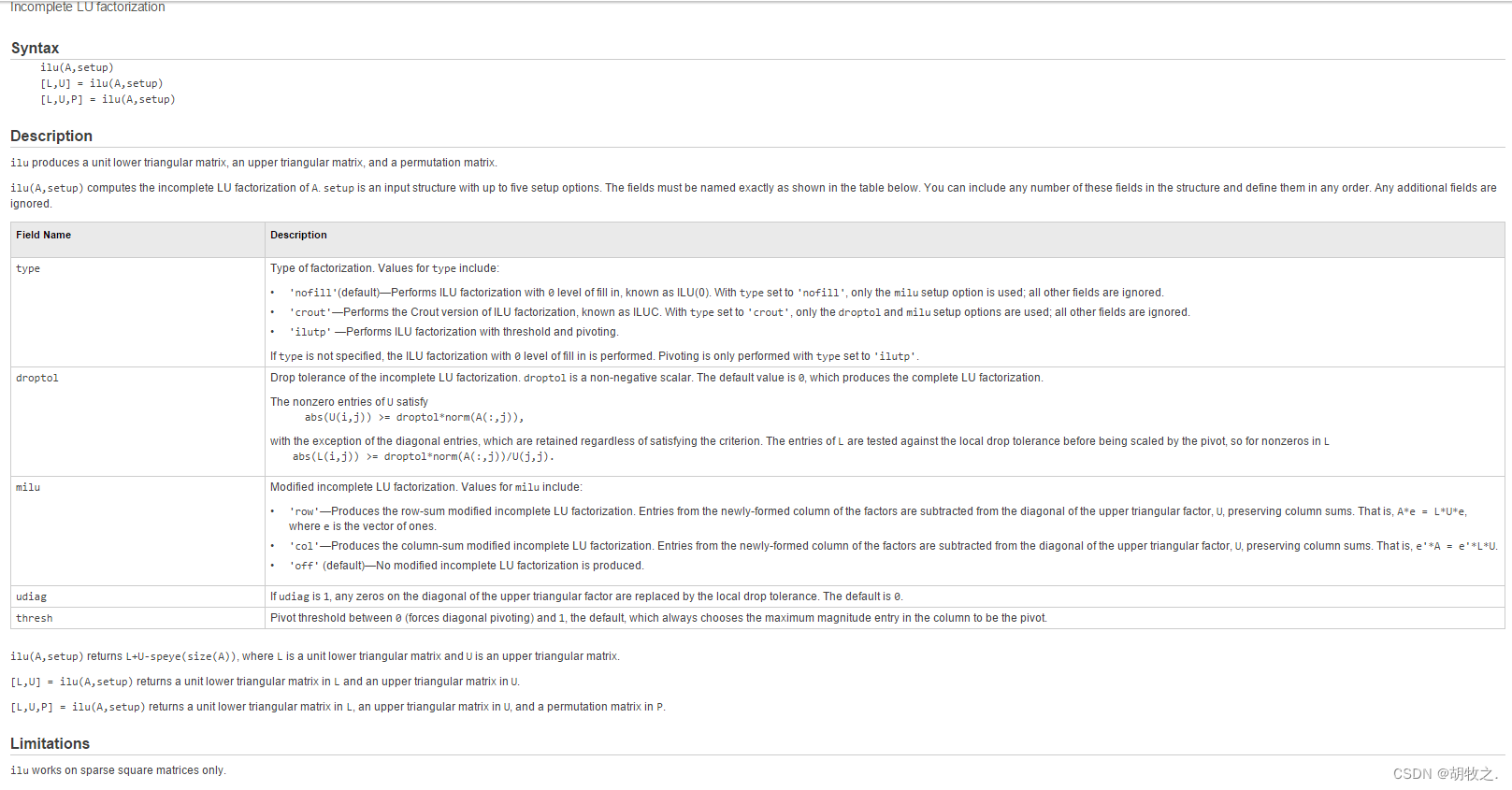
(四)稀疏矩阵的不完全LU分解 luinc()/ilu()

与上方cholinc()原因类似,如今只有ilu()
(五)矩形矩阵的正交分解(QR分解) qr()
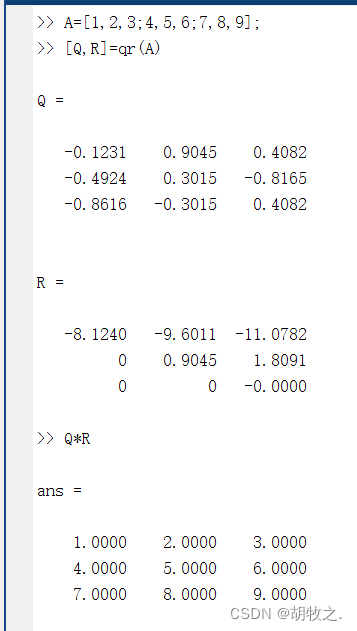
Q R QR QR分解把一个 m × n m \times n m×n的矩阵 A A A分解为一个正交矩阵 Q Q Q和一个上三角矩阵 R R R的乘积,即 A = Q × R A=Q \times R A=Q×R
函数qr()可以实现QR分解,其调用方式如下:
[Q,R]=qr(A) R为与A具有相同大小的上三角矩阵,Q为正交矩阵,满足A=Q*R,该调用方式适合满矩阵和稀疏矩阵
[Q,R]=qr(A,0) “经济”的QR分解,设A为m*n的矩阵,若m>n,则只计算Q的前n列元素,R为n*n的矩阵;否则,功能与上式一样
R=qr(A) 返回上三角矩阵R,这里 R=chol(A'*A),该调用方式适合稀疏矩阵
R=qr(A,0) 以上述“经济”的方式进行分解
[Q,R,E]=qr(A) E为置换矩阵,满足A*E=Q*R,程序会选择一个合适的矩阵E使得abs(diag(R))为降序排列,该方法适合满矩阵
[Q,R,E]=qr(A,0) 以上述“经济”的方式进行分解,E为置换矢量,满足A(:,E)=Q*R,该方法适合满矩阵
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9

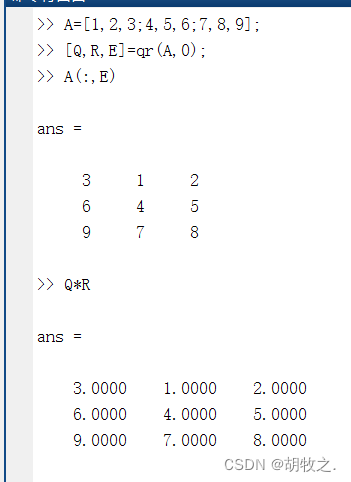
(六)舒尔分解 schur()
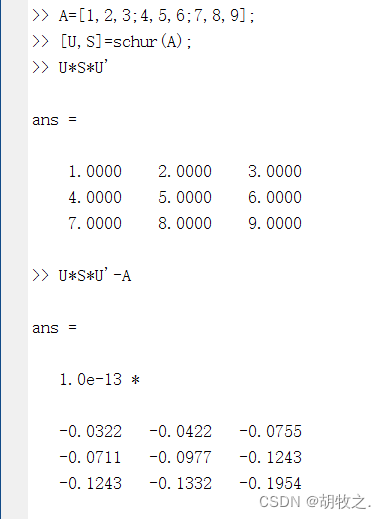
舒尔分解的定义式为:
A
=
U
∗
S
∗
U
′
A=U*S*U^{'}
A=U∗S∗U′,其中
A
A
A必须是一个方阵,
U
U
U是一个酉矩阵,
S
S
S是一个块对角化矩阵,由对角线上的
1
×
1
1\times1
1×1和
2
×
2
2\times2
2×2块组成
特征值可以由矩阵
S
S
S的对角块给出,而矩阵
U
U
U给出比特征向量更多的数值特征
此外,对缺陷矩阵也可以进行舒尔分解
缺陷矩阵:不可对角化矩阵
函数schur()可以进行舒尔分解,其调用格式如下:
[U,S]=schur(A) 返回酉矩阵U和块对角化矩阵S
S=schur(A) 仅返回块对角矩阵S
schur(A,'real') 返回的实特征值放在对角线上,而把复特征值放在对角线上的2*2块中
schur(A,'complex') 返回的矩阵S是上三角矩阵,并且如果矩阵A有复特征值,则矩阵S是复矩阵
- 1
- 2
- 3
- 4
- 5
- 6
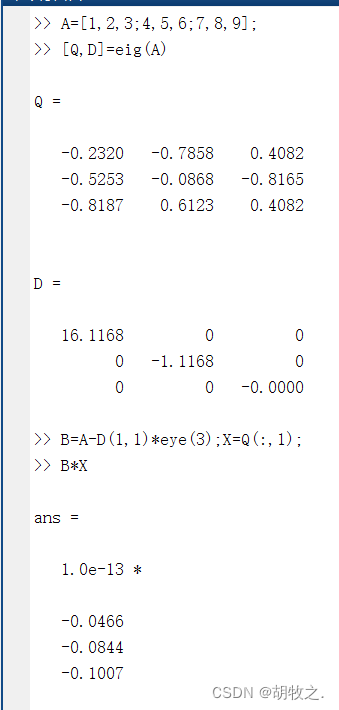
八、特征值和特征向量 eig()
(一)定义
A
A
A为
n
n
n阶矩阵,
λ
\lambda
λ为实数,若我们可以找到一个非零向量
x
x
x,使得
A
x
=
λ
x
Ax=\lambda x
Ax=λx,我们就称
λ
\lambda
λ为矩阵
A
A
A的特征值,非零向量
x
x
x为矩阵
A
A
A的特征向量
从几何角度来说,
A
x
Ax
Ax与
x
x
x的方向相同,只是长度不同,而长度相差的就是系数
λ
\lambda
λ,
(二)相关矩阵


(三)计算

九、稀疏矩阵
(一)概念
对于含有大量 0 0 0元素的稀疏矩阵, M A T L A B MATLAB MATLAB为了节省空间和计算时间,对稀疏矩阵运算有特殊的命令
(1)节省空间
如果
M
A
T
L
A
B
MATLAB
MATLAB把一个矩阵当作稀疏矩阵,若有
m
m
m个非零项,则可以通过一个
m
×
3
m\times3
m×3的矩阵来存储,第一列为行下标,第二列为列下标,第三列为非零元素值
(2)节省时间
之前所说的算术和逻辑运算都适用于稀疏矩阵,相对于普通矩阵,稀疏矩阵的计算速度更快,因为MATLAB只需对非零元素进行操作
(二)存储方式
对于稀疏矩阵, M A T L A B MATLAB MATLAB仅存储矩阵所有的非零元素的值及其位置,一个矩阵越“稀疏”,其节省空间的效果就越明显
(三)稀疏矩阵创建 sparse()


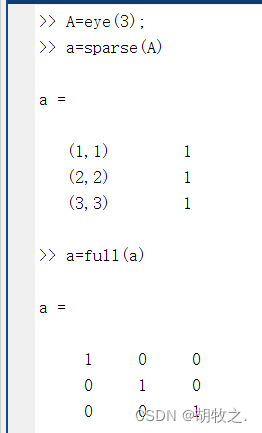
(四)稀疏矩阵的属性查看
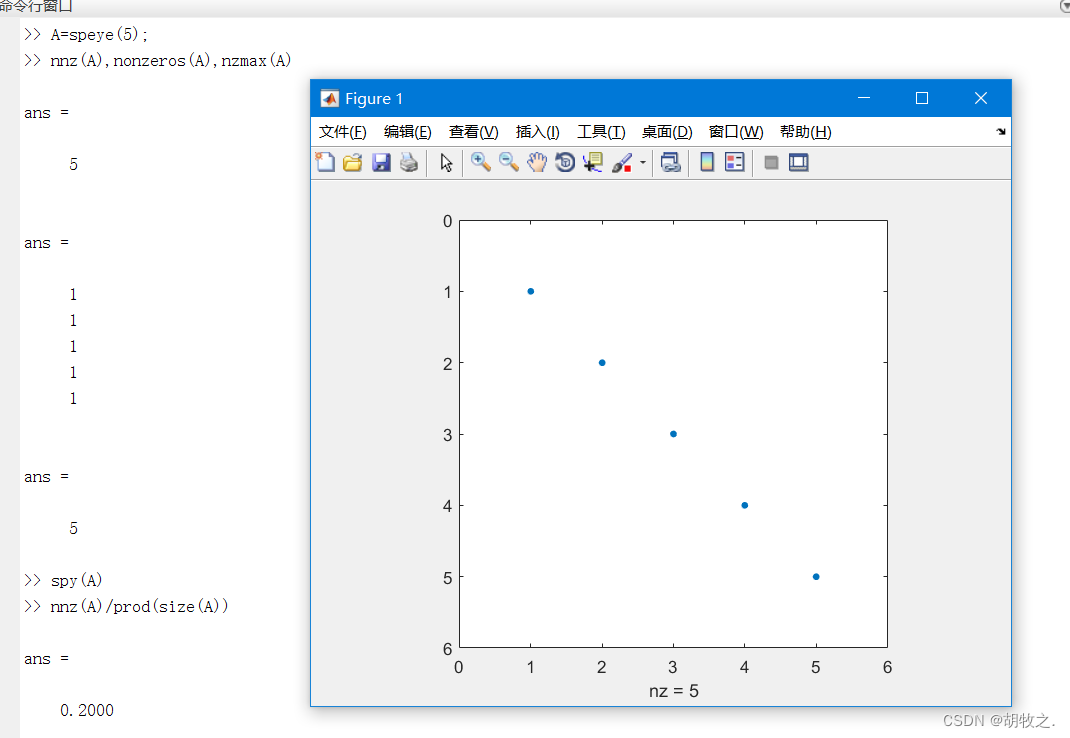
nns(A) 查看稀疏矩阵中非零元素个数
nonzeros(A) 查看稀疏矩阵中非零元素的值,返回一个向量
nzmax(A) 查看稀疏矩阵的存储空间
nnz(A)/prod(size(A)) 可以计算稀疏矩阵的非零元素密度
spy(A) 对稀疏矩阵中的非零元素的分布进行图形化显示
- 1
- 2
- 3
- 4
- 5
- 6
(五)稀疏矩阵的运算(结果形式的确定)
对于矩阵的加减乘除运算,只要其中有一个是满矩阵,输出结果就是满矩阵
稀疏矩阵的数乘为稀疏矩阵,稀疏矩阵的幂为稀疏矩阵
- 1
- 2




