ltb火箭_火箭的大脑

Two ideas from computer science have intrigued me for a long time: neural networks and evolutionary algorithms. Neural networks are of course everywhere right now: essentially a computer runs a “brain” consisting of simulated nerve cells. They are being used to perform science-fiction-sounding tasks like besting human grand masters in games¹, creating natural looking landscapes from sketches² or even photos of people that don’t exist³. The concept behind evolutionary algorithms is possibly even more fascinating: a population of computer programs is tested against each other in a simulation of natural selection, and over time the descendants of the “survivors” become increasingly better at their required task. Although they are a bit less all-present than neural networks evolutionary algorithms have their applications, and sometimes both are used together.

很长一段时间以来，计算机科学的两个想法吸引了我：神经网络和进化算法。 神经网络当然现在无处不在：本质上，一台计算机运行由模拟神经细胞组成的“大脑”。 它们被用来执行听起来像科幻小说般的任务，例如在游戏中击败人类大师，用草图2甚至是不存在的人的照片3创造出自然的风景。 进化算法背后的概念可能更令人着迷：在自然选择的模拟中，对计算机程序进行了相互测试，随着时间的流逝，“幸存者”的后代在其所需任务上变得越来越出色。 尽管它们比神经网络的通用性要差一些，但进化算法却有其应用，有时两者一起使用。

Neural networks and evolutionary algorithms in their simplest forms can be programmed in surprisingly few lines of fairly straightforward code. Both are notorious for requiring a lot of computing power, but today’s computers should be plenty powerful enough to deal with a small problem even if the program runs in a web browser (or so I assumed). If I had an interesting problem to solve I could make an entertaining personal project that shouldn’t take lots of coding to complete, or so I hoped!

最简单形式的神经网络和进化算法可以用几行相当简单的代码进行编程。 两者都因需要大量的计算能力而臭名昭著，但是，即使程序在Web浏览器中运行(或者我假设是这样)，当今的计算机也应具有足够强大的功能来处理一个小问题。 如果我有一个有趣的问题要解决，那么我可以做一个有趣的个人项目，而无需花费很多代码来完成，所以我希望如此！

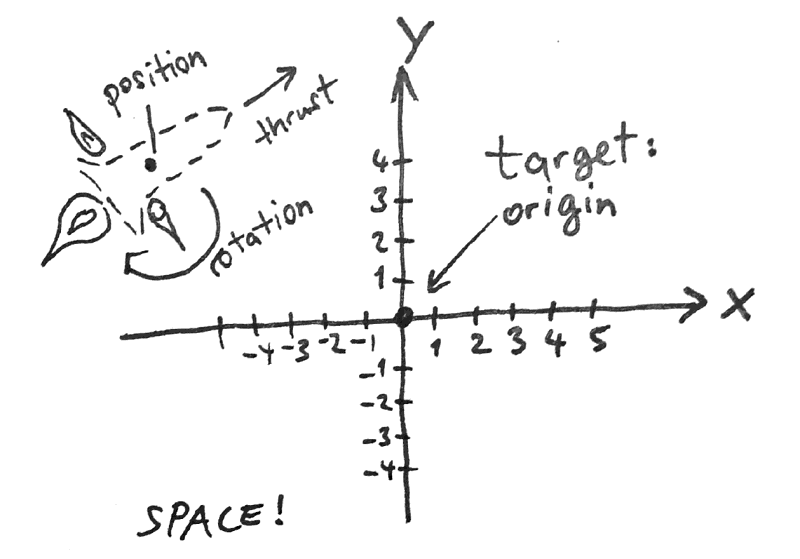
So I tried to come up with a very simple problem that’s also fun to look at. If it could become part of a video game, even better! The objective: hit a target (possibly an enemy UFO) with a homing rocket (possibly fired by the hero’s spaceship). It’s in “space”, a two-dimensional flat plane where the rocket is “fired” starting at some random position and the target is always at the origin of the coordinate system. The rocket can’t fly just any which way but rather experiences simulated (simplified) physics that allows believable (at least to me!) flying behavior. It needs a homing device that controls its main engine, which drives it forward, and two attitude jets on the sides that rotate it. Due to inertia the rocket will keep flying or rotating until the engines counteract that movement, so the homing device needs to take into account how the rocket is moving at all times to steer it successfully. This is definitely solvable in a variety of ways using handmade code, but I was curious how my neural network would handle it, if it could at all.

因此，我试图提出一个非常简单的问题，这个问题也很有趣。 如果它可以成为视频游戏的一部分，那就更好了！ 目标：用寻的火箭(可能由英雄的太空飞船发射)击中目标(可能是敌人的UFO)。 它在二维的平面“空间”中，从某个随机位置开始“发射”火箭，目标始终位于坐标系的原点。 火箭不能以任何方式飞行，而是要经历模拟的(简化的)物理过程，从而可以实现(至少对我来说)飞行行为。 它需要一个控制其主引擎并使其向前驱动的归位装置，并在使它旋转的侧面上有两个姿态喷嘴。 由于惯性，火箭将一直飞行或旋转，直到发动机抵消该运动为止，因此制导装置需要考虑到火箭始终在如何运动以使其成功转向。 使用手工代码，这绝对可以通过多种方式解决，但是我很好奇我的神经网络将如何处理它，如果可以的话。

This project was made in JavaScript and runs on Firefox or Chrome browsers. You can find the source code here: https://github.com/rkibria/evolvenn

该项目使用JavaScript制作，可在Firefox或Chrome浏览器上运行。 您可以在这里找到源代码： https : //github.com/rkibria/evolvenn

First I needed a working rocket simulation that was in a sweet spot of “complex enough” so that the rocket’s behavior is interesting but short of “needlessly complicated” which would increase the amount of code to write. The simulation’s complexity also affects how many inputs the neural network will have, unless we are willing to leave out some information, which I wanted to avoid.

首先，我需要一个工作火箭仿真，该仿真处于“足够复杂”的最佳点，这样火箭的行为很有趣，但缺少“不必要的复杂”，这会增加编写代码的数量。 除非我们愿意遗漏一些我想避免的信息，否则模拟的复杂性还会影响神经网络将有多少输入。

The simulation uses 7 numbers (stored as 3 two-dimensional vectors and 1 number) to describe the rocket’s state:

模拟使用7个数字(存储为3个二维向量和1个数字)来描述火箭的状态：

• Position vector (where the rocket is). This changes according to the current velocity.
  位置向量(火箭所在的位置)。 这根据当前速度而变化。
• Velocity vector (where the rocket is moving). This changes according to the current main engine’s thrust as well as the direction the rocket is facing.
  速度矢量(火箭移动的位置)。 这会根据当前主机的推力以及火箭所面对的方向而变化。
• Direction vector (where the nose points). This changes depending on the current angular velocity.
  方向向量(鼻子指向的位置)。 这根据当前角速度而变化。
• Angular velocity (turning speed). This changes depending on the attitude jets’ thrust.
  角速度(转弯速度)。 这取决于姿态喷气机的推力而变化。

These numbers will be fed to the neural network, which will compute from them how the engines fire. Two numbers control the engines:

这些数字将被馈送到神经网络，该神经网络将从中计算出引擎如何点火。 两个数字控制引擎：

• Acceleration (main engine thrust). If this is zero then the engine is idle, otherwise the velocity increases. Can only be positive.
  加速(主机推力)。 如果为零，则发动机空转，否则速度增加。 只能是积极的。
• Rotation (attitude jet thrust). If this is zero then both jets are idle, otherwise one of the jets will thrust to turn the rocket clockwise or counter-clockwise.
  旋转(姿态射流推力)。 如果该值为零，则两个喷气机均处于空闲状态，否则其中一个喷气机将推动以顺时针或逆时针方向旋转火箭。

As I found out later it was also necessary to introduce some sanity checks to avoid the rocket accelerating into infinity or turning so fast it looks like just a circle on the screen. Therefore the velocity as well as the angular velocity were locked to a maximum beyond which the engines will not push them.

正如我后来发现的那样，还必须进行一些完整性检查，以免火箭加速到无穷大或转动得如此之快，使其看起来像是屏幕上的一个圆圈。 因此，速度和角速度都被锁定在一个最大值，超过该最大值引擎将不会推动它们。

The whole system is linked up like this:

整个系统是这样链接的：

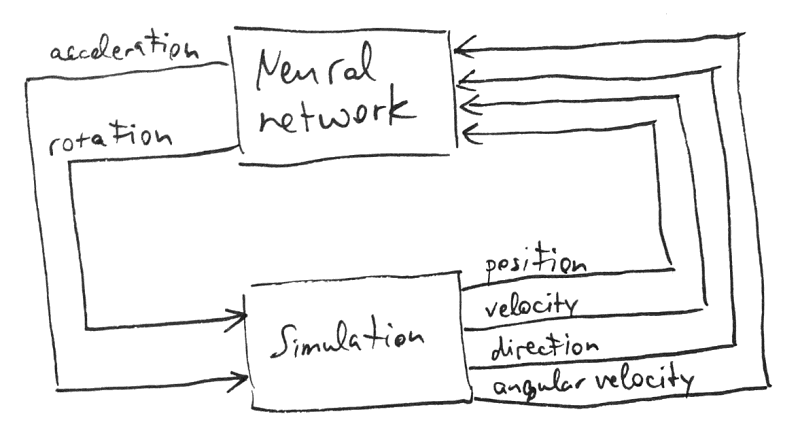
When the program runs we read the current rocket state from the simulation at every time step and pass it through the neural network, which yields the rocket control values that we feed back to the simulation.

当程序运行时，我们会在每个时间步长从仿真中读取当前的火箭状态，并将其通过神经网络传递，这会产生火箭控制值，并反馈给仿真。

Now let’s build the actual neural network!

现在让我们构建实际的神经网络！

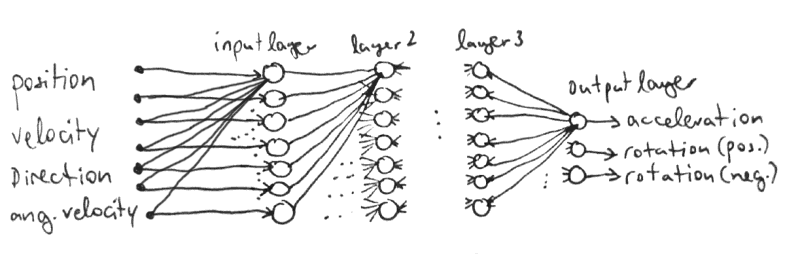
Neural networks are organized as layers of their basic elements, the neurons, which are very simplified models of nerve cells. Each neuron has a number of inputs and one output. The inputs are each associated with a constant number, the weights. The neuron sums up all inputs multiplied by the associated weight, and adds a flat bias value on top. Then the output of the neuron is the sum run through the neuron’s activation function: I used the rectifier⁴ which is equal to the sum if it’s larger than zero, or otherwise zero.

神经网络被组织为神经元的基本元素层，神经元是神经细胞的非常简化的模型。 每个神经元具有多个输入和一个输出。 每个输入都与一个常数，权重相关联。 神经元将所有输入相加并乘以关联的权重，然后在顶部添加一个平坦的偏置值。 然后，神经元的输出是通过神经元的激活函数运行的总和：我使用的整流器if等于和，如果它大于零，或者大于零。

I am using a simple feedforward neural network setup where the inputs “ripple” through the layers starting from the inputs and come out the other end as outputs. The rocket simulation’s 7 output values will be the neural network’s inputs, and it should output 2 rocket control values to feed back to the simulation. However, as I found out from experimentation the rotation output presented a problem: as mentioned above it is supposed to be either negative to turn the rocket one way or positive to turn it the other way. This didn’t work very well and my rocket ended up only ever turning one way or not at all. Therefore I split up the rotation output into two outputs: one turns the rocket one way and the other the other way. Both are positive, but whichever is higher “wins” and turns the rocket its way, while the other output is ignored. So I ended up with 3 neural network outputs instead of 2, which have to be processed before passing the final 2 values to the simulation.

我正在使用一个简单的前馈神经网络设置，其中输入从输入开始“遍历”各层，并在另一端作为输出。 火箭模拟的7个输出值将是神经网络的输入，并且应该输出2个火箭控制值以反馈给模拟。 但是，正如我从实验中发现的那样，旋转输出带来了一个问题：如上所述，应该以一种方式使火箭旋转为负值，或者以另一种方式旋转为正值。 这不是很好，我的火箭最终只转过一个方向或根本不转。 因此，我将旋转输出分为两个输出：一个旋转火箭的方式，另一个旋转火箭的方式。 两者均为正数，但取其高者“获胜”，使火箭前进，而其他输出则被忽略。 因此，我最终得到了3个神经网络输出，而不是2个，必须在将最后2个值传递给仿真之前进行处理。

There was another range-related problem on the input side. The position input has a higher range of values than the others since it can reach e.g. high hundreds or more whereas the rest stay an order of magnitude or more lower. This seemed to hinder finding good solutions, so I added a logarithmic scaling to reduce the effective range of these two inputs.

在输入端还有另一个与范围相关的问题。 位置输入具有比其他值更高的值范围，因为它可以达到例如数百或更高，而其余位置则保持一个数量级或更低。 这似乎阻碍了找到好的解决方案，因此我添加了对数缩放以减小这两个输入的有效范围。

This leaves the question of how many layers of neurons do I need? There is no precise answer to this⁵ and I arrived at using a total of 4 layers by trial and error. The first 3 layers (starting with the input layer) each have 7 neurons and the last layer (the output layer) has 3.

剩下的问题是我需要多少层神经元？ 对此没有确切答案，我通过反复试验得出了总共使用4层的结论。 前3层(从输入层开始)每个都有7个神经元，最后3层(输出层)有3个神经元。

Now the network’s high level architecture is decided it still needs to be able to solve the problem. This means the weight and bias values have to be assigned, of which there are rather many: in total we have 3 x (7 x 8) + 3 x 8 = 192 numbers to assign. Clearly too many to find by trial and error! This is where the evolutionary algorithm comes in.

现在，网络的高级体系结构已决定仍然需要能够解决该问题。 这意味着必须分配权重和偏差值，其中有很多：总共需要分配3 x(7 x 8)+ 3 x 8 = 192个数字。 显然，通过反复试验找不到太多！ 这就是进化算法的用武之地。

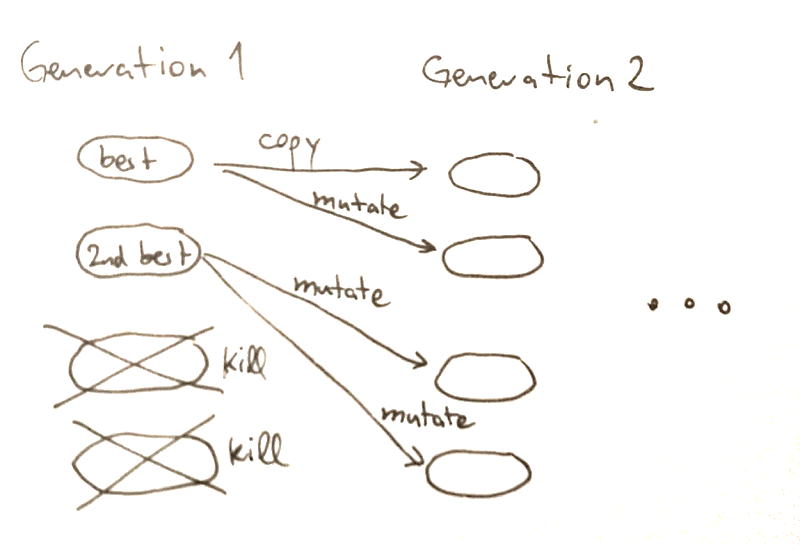
At the heart of the evolutionary algorithm is a very simple loop:

进化算法的核心是一个非常简单的循环：

1. Start with a population of solutions to our problem encoded in a way that supports mutating them.

   开始的方式，支持突变它们编码到我们的问题解决方案的人口。

2. Test every solution in the current population on a set of example problems. Assign each a fitness which is a number that measures how well the solution solves the problems.

   在一系列示例问题上测试当前总体中的每个解决方案。 为每个适应度分配一个数字，该数字可以衡量解决方案解决问题的程度。

3. Sort the solutions by fitness and “kill off” some percentage of the worst solutions. Fill the population up afterwards to the starting size with “offspring”, i.e. copies of the remaining solutions that have also been mutated. This is the next generation. Go to step 2 if the best solution found so far isn’t good enough, otherwise stop.

   按适合度对解决方案进行分类，并“杀死”一些最差的解决方案。 然后用“后代”填充种群，直至达到初始大小，即也已突变的其余溶液的副本。 这是下一代。 如果到目前为止找到的最佳解决方案还不够好，请转到步骤2，否则请停止。

It’s expected that over time the population fills up with better and better solutions, hopefully including one that solves the problem at hand “well enough” so that we can stop. Since this is essentially a random search we can not guarantee to find an optimal solution and may need to run the algorithm many times.

预计随着时间的流逝，人们会找到越来越好的解决方案，希望其中包括“足够好”地解决当前问题的解决方案，以便我们能够制止。 由于这本质上是随机搜索，因此我们无法保证找到最佳解决方案，因此可能需要多次运行该算法。

There are quite a few design decisions to make here. My implementation did the following, going for simplicity of implementation foremost:

这里有很多设计决策。 我的实现执行以下操作，以简化实现为首要任务：

• The solution encoding is a list of 192 floating point numbers (the neural network weights). Mutation means that I randomly vary each number in the list by a small amount up or down. The first generation starts with random numbers for every one of the list values.
  解决方案编码是192个浮点数(神经网络权重)的列表。 变异是指我将列表中的每个数字随机上移或下移少量。 第一代从每个列表值的随机数开始。
• The population size is 1000 solutions.
  人口总数是1000个解决方案。
• Step 3 always kills the worse half of the population. The “parents” are the other half, which create two offspring each, except the very best solution which is copied unchanged into the next generation.
  步骤3总是杀死更坏的一半人口。 “父母”是另一半，每个人都产生两个后代，除了最好的解决方案，该解决方案被原样复制到下一代中。
• The mutation “rate” (how much an offspring will differ from the parent) changes over time. We have a high mutation strength at the start which halves every 100 generations. This was quite important for getting good solutions. The effect of this is that we try out very different solutions early on but concentrate on refining already good solutions later.
  变异“比率”(后代与亲本的差异多少)随时间变化。 一开始我们的突变强度很高，每100世代减半。 这对于获得良好的解决方案非常重要。 这样做的结果是，我们尽早尝试了非常不同的解决方案，但稍后集中精力完善已经很好的解决方案。

Assigning the fitness was not a straightforward endeavor and required quite a lot of trial and error until I got good solutions:

分配适应性并不是一件容易的事，在我得到好的解决方案之前，需要大量的反复试验：

• Set initial fitness = 0. Set the initial rocket position somewhere not at the origin.
  设置初始适应度=0。将初始火箭位置设置在原点以外的位置。
• Run the simulation for up to 10 seconds (effective time, not actual wall clock time). This equates to 600 simulation time steps, assuming 60 frames per second when running the graphical simulation.
  运行模拟最多10秒钟(有效时间，而不是实际的墙上时钟时间)。 假设运行图形仿真时假设每秒60帧，则相当于600个仿真时间步长。

• The rocket has hit the target if its position is within 20 units (half of drawn rocket length) to the origin. Stop the computation if hit but only if the rocket is hitting nose first. If not hitting nose first add 20 to the fitness and continue.

  如果火箭的位置在距原点20个单位(火箭抽出长度的一半)以内的位置，则已击中目标。 如果被击中，则仅在火箭先击中鼻子时停止计算。 如果没有撞到鼻子，请先增加20并继续。

• If not hit, add the current distance to the origin minus 20 to the fitness score.
  如果未命中，则将当前距离减去原点后再减去20。
• After either 10 simulated seconds have passed or we hit the target multiply the fitness by 1 + steps taken / 60. If not hit in the 10 seconds double the fitness again.
  经过10个模拟秒或我们达到目标后，将适应度乘以1 +步数/60。如果在10秒内未击中目标，则再次使适应度翻倍。

The cumulative effect of these abstract rules is roughly “good solution get close to the center quickly and hit it nose first”. You may notice that the fitness value actually is higher for “bad” solutions: this is because traditionally evolutionary algorithms look for the lowest fitness value. This is a good fit here anyway but would be simple to fix if we wanted to look for the highest value instead.

这些抽象规则的累积效果大致是“一个好的解决方案会Swift靠近中心并首先达到目标”。 您可能会注意到，“不良”解决方案的适应度值实际上更高：这是因为传统上进化算法会寻找最低适应性值。 无论如何，这是一个很好的选择，但是如果我们想寻找最高值，那么将很容易解决。

Now both the neural network and the evolutionary algorithm are implemented, but how do we use this to find a solution that “always works”? Consider that in the description of the evolutionary algorithm we start the rocket at some (single) point, and generate a neural network weights set that can steer it from that point to the origin. What happens though if we don’t start at that exact point but somewhere slightly away from it, or even on the other side of the coordinate system? Unfortunately solutions that were generated for just one starting point do not work at all for anything else, the neural network is not general enough to “know what to do”.

现在，神经网络和进化算法都已实现，但是我们如何使用它来找到“始终有效”的解决方案？ 考虑到在进化算法的描述中，我们从某个(单个)点启动了火箭，并生成了一个神经网络权重集，该权重集可以将火箭从该点引向原点。 但是，如果我们不是从那个精确的点开始，而是稍微偏离它的某个地方，甚至在坐标系的另一侧，会发生什么？ 不幸的是，仅针对一个起点生成的解决方案根本无法用于其他任何事情，神经网络的通用性不足以“知道该做什么”。

How do we make it more general? Let’s assume a whole set of starting points and then running the fitness evaluation for each one, summing up the total fitness. If a solution has a good fitness for e.g. 100 starting points we could reasonably expect that the neural network has learned some general rules how to steer the rocket from anywhere rather than just “storing” a course that works for a single point. It’s not hard to make a loop over a large set of starting points like this, but this increases the computation times into unfeasible regions. Testing this approach with smaller sets of randomly placed starting points also showed that the resulting solutions were of poor quality, barely distinguishable from the single starting point solutions.

我们如何使其更通用？ 让我们假设一整套起点，然后对每个起点进行适应性评估，以总结出总体适应性。 如果某个解决方案适合于100个起点，那么我们可以合理地预期神经网络已经学到了一些通用规则，该规则指导如何从任何地方操纵火箭，而不仅仅是“存储”适用于单个点的路线。 像这样在一大堆起点上进行循环并不难，但这会增加不可行区域中的计算时间。 用较小的一组随机放置的起点测试此方法还表明，所得解决方案的质量较差，与单个起点解决方案几乎没有区别。

After more trial and error I found a compromise that worked:

经过更多的尝试和错误之后，我发现了一个可行的折衷方案：

1. Start with a single starting point, at a position just slightly below the origin.
   从一个起点开始，在一个稍微低于原点的位置。
2. Run the evolutionary algorithm until we have a solution that hits the target for every current starting point MINUS ONE. It was important not to require hitting for every starting point because sometimes the algorithm seemed not to find a way to make it happen and got stuck.
   运行进化算法，直到找到一个针对每个当前起点减一的目标。 重要的是，不要要求每个起点都命中目标，因为有时该算法似乎没有找到实现它的方法并被卡住。
3. If we hit enough times, add an additional starting point. The new point is at the same position as the last one, but starts the rocket with the nose pointing in a different angle. Do this up to 4 times. After that, place the next point on a circle at the same radius as the last point. Repeat this until the circle is full, after that increase the radius by some amount and start with a point below the origin at this radius. ALSO every time we add a new point randomly vary the positions of every previous starting point by a small amount. This seemed to be important to make more general solutions.
   如果我们击中次数足够多，请添加一个额外的起点。 新点与最后一个点在同一位置，但以鼻子指向不同的角度启动火箭。 最多执行4次。 之后，将下一个点放置在与最后一个点相同半径的圆上。 重复此操作，直到圆充满为止，然后将半径增加一些，并从该半径处的原点以下的点开始。 另外，每当我们添加一个新点时，都会随机地将每个先前起点的位置稍微改变一点。 这对于制定更通用的解决方案似乎很重要。

This is the progress for a program run using this approach, sped up:

这是使用这种方法运行的程序的进度，加快了速度：

演示地址

You can run the algorithm from this page: https://rkibria.github.io/evolvenn/evolve.html (warning, quite heavy on the browser!).

您可以从以下页面运行该算法： https : //rkibria.github.io/evolvenn/evolve.html (警告，在浏览器上非常繁琐！)。

Since evolutionary algorithms are random searches that are likely to find some adequate solution but not always necessarily the optimal one it was not unexpected that many solutions were outright bad. Additionally there were also some that, though they do the job, were odd and not really “rocket-like” behavior:

由于进化算法是随机搜索，可能会找到一些适当的解决方案，但不一定总是最佳解决方案，因此，许多解决方案绝对是不好的，这并不意外。 此外，还有一些虽然可以胜任的工作却很奇怪，而且并不是真正的“火箭式”行为：

• Early on, especially before I locked the maximum rotation speed down to a sane value, there were a lot of solutions that made the rocket spin like a Catherine wheel firework and fired the main engine only in the tiny moments it was pointed in a line to the center so that effectively the rocket had omnidirectional main thrust.
  早期，特别是在我将最大转速降低到合理值之前，有许多解决方案使火箭像凯瑟琳轮式烟花一样旋转，并仅在对准直线的微小时刻才对主机进行点火从而使火箭有效地具有全向主推力。
• After locking down the rotation speed there were a lot of solutions that still constantly spun and fired the main engine in a pattern that forward-then-sideways tumbled the rocket to the target a bit like a knight in chess.
  锁定转速后，仍然有许多解决方案仍在不断旋转并以某种方式发射主发动机，然后向前-向侧面倾斜，使火箭像国际象棋中的骑士一样跌落至目标。
• Some solutions looked mostly good except they would sometimes exhibit an odd “walking” behavior where the rocket would move almost straight sideways using only an attitude jet.
  一些解决方案看起来大多不错，除了它们有时会表现出奇怪的“行走”行为，即仅使用姿态射流，火箭几乎可以向侧面移动。
• When I tried to reward the algorithm for hitting the target with maximum speed and head on the rocket would always travel from wherever it started to some far point on one side of the target, then accelerate massively and hit from the same direction every time.
  当我尝试奖励以最大速度击中目标的算法时，火箭的头部始终会从它开始的位置行进到目标一侧的某个较远点，然后大幅度加速并每次都从相同方向击中。

But eventually I got a solution that would hit the target fairly consistently starting from any point and looked reasonably realistic:

但是最终，我得到了一个从任何时候都可以始终如一地达到目标的解决方案，并且看上去相当现实：

演示地址

Try it out live on this page: https://rkibria.github.io/evolvenn/neural_sim.html (press the “Randomize pos.” button to place the rocket in a random location and restart the simulation).

在此页面上进行实时尝试： https : //rkibria.github.io/evolvenn/neural_sim.html (按“ Randomize pos。”(随机位置)按钮将火箭放置在随机位置并重新启动模拟)。

Thank you for reading!

感谢您的阅读！