PID参数自整定库之一：继电反馈整定算法_relay feedback method pid

  在前述的篇章中，我们实现了PID控制器并在后续对其进行了改进。但作为经典PID控制器还存在PID参数整定的问题。通常我们可以采取人工整定的办法，但人工整定涉及到比较专业的知识，而且找到合适的参数本身也不是一件容易的事，所以人们探索了一系列适用于不同情况的PID参数自动整定算法。在这一篇中我们就来讨论基于继电反馈的PID参数自整定算法。

1、基本原理

  若测出了系统的一阶模型，或得出了系统的临界比例增益Kc和振荡周期Tc，则可很容易地设计出PID调节器。

1.1、继电反馈自整定过程

  继电反馈自整定的基本思想是，在控制系统中设置两种模式：整定模式和调节模式。很显然，调节模式就是指我们正常使用的PID控制器，而整定模式就是我们用以整定PID参数的过程。
  在整定模式下，我们将系统的操作转换为开关方式，即输出值在最大值和最小值之间周期性的转换。具体来说就是当测量值小于设定值时，我们将控制器的输出最大，而当测量值大于设定值之后我们又将输出值设为最小。这样被控系统聚会产生振动，经过至少3次过零检测，我们就会得到一个周期的振荡波型，从这个振荡波形中，我们可以提取到系统的特征参数，从而得到我们想要的PID参数。
  在调节模式下，由系统的特征参数首先得出PID控制器的参数，然后使用此PID控制器对系统进行调节。PID参数继电反馈自整定的结构图如下：

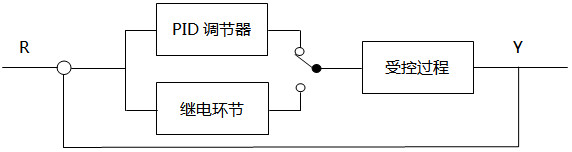
  从上图中我们可以知道，当需要PID参数整定时，开关置于继电环节，系统按继电反馈建立起稳定的极限环振荡后，就可以根据系系统响应特征确定PID参数。而当自整定计算完成后，我们可以控制开关置于PID调节器环节，这样系统进入正常PID控制过程。

1.2、继电反馈自整定的原理

  为什么我们采用这一方式就可以确定PID控制器的参数呢？这是因为振荡波形的特性是由被控对象的特性决定的。在整定模式下，我们可以将整个控制系统的框图等效如下：

  当我们根据测量值与设定值的对比关系来给出最大或最小输出时，基于被控对象的特性会产生一定频率和幅值的振荡波，从而我们就能确定系统的振荡频率ωc与临界增益Kc。比较常用的确定系统的振荡频率ωc与增益Kc的方法是描述函数法。所谓描述函数法，实际上是根据非线性环节输入信号与输出信号之间基波分量关系来进行近似的一种有效方法。
  关于非线性特征的描述函数N(A)来说，就是当输入是正弦信号Asin(ωt)时，输出的基波分量Ysin(ωt+φ)对输入正弦量的复数比，即：

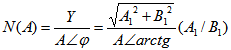
  其中A1、B1是输出Y(t)的傅立叶级数的一次项系数。
  实际的带有回环的节点非线性环节特性的描述函数可以表示为：

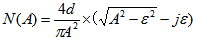
  公式中A为正弦波幅值，d为回环幅值，ε为回环宽度的一半。这里我们构建继电环节时，我们可以认为它是一个理想的继电环节，也就是说不带有回环，即ε=0，于是就有：

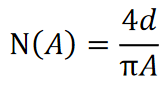
  在这里我们设被控对象的传递函数为如下形式：

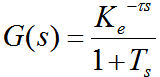
  其中K为对象的增益，T为对象的时间常数，τ为对象的滞后时间。
  根据前面继电回路结构框图，在这个简单的反馈系统中，闭环特征方程发生振荡的条件可以写为：
1+N(A)G(s)=0 (s=jωc)，即G(jωc)=-1/N(A)。
  则可得出振荡频率ωc与增益Kc为：

  系统的振荡周期Tc可以通过测量输出曲线相邻峰值的时间得到。至此我们就得到了临界频率ωc所对应的临界增益和临界振荡周期。
  在得到被控对象的临界增益和临界振荡周期后，就可以根据Ziegle-Nichols算法确定PID参数。如表所示：

  这样，就用继电反馈的方法整定出了PID调节器参数。PID参数继电自整定法是一种简单的自适应控制方法，它所需要的数据量小，实现简单，调节效果好，特别适用于内存量较小的调节器，因而得到广泛的应用。

2、算法设计

  我们已经明白了PID参数继电反馈自整定的基本原理，那么我们究竟如何实现呢？在接下来我们就来设计基于继电反馈PID参数自整定的具体实现算法。
  使用继电反馈方法整定PID参数主要涉及到两个方面的内容。第一是通过人为操作让系统产生临界振荡，这是测量出临界比例Kc和临界周期Tc的根本所在。第二是根据得到的数据计算PID参数的值。所以我们就从这两个方面的内容来考虑基于继电反馈的PID参数整定算法。

2.1、振荡的生成

  首先我们来看分析振荡波形如何产生。在继电反馈中，要产生振荡都是通过控制执行单元以一定的输出比例来回转换而是测量值随之振荡。所以我们在系统中给定一个设定值后，我们根据设定值与测量值之间的偏差来决定输出值是正向最大还是反向最大。
  在这里我考虑执行单元为正作用的情况，一般在设定值大于测量值时，我们将执行单元的输出切换到相应的高输出，这时测量值将会随之而上升。当测量值上升到大于设定值时，我们将执行单元的输出切换到相应的低输出，这时测量值将会随之而下降。如此往复，我们就能得到测量值的振荡曲线。
  在每次切换执行单元的时候，我们记录一次转换次数。同时观察测量值与设定值的相对大小，每次测量值由大于设定值变为小于设定值，或者由小于设定值变为大于设定值都称之为一次过零。如果我们检测到4次过零，或者说5次切换执行单元，则我们就可以认为系统产生了振荡。
  进一步考虑我们发现，整定开始时测量值与设定值所处的相对位置对于我们的判断有关键影响。如果初始时，测量值大于设定值，则在两次过零后会出现最大值，如下图的区域3的位置。而在3次过零后会出现最小值，如下图的区域4的位置。

  如果初始时，测量值小于设定值，则在两次过零后会出现最小值，如下图的区域3的位置。而在3次过零后会出现最大值，如下图的区域4的位置。

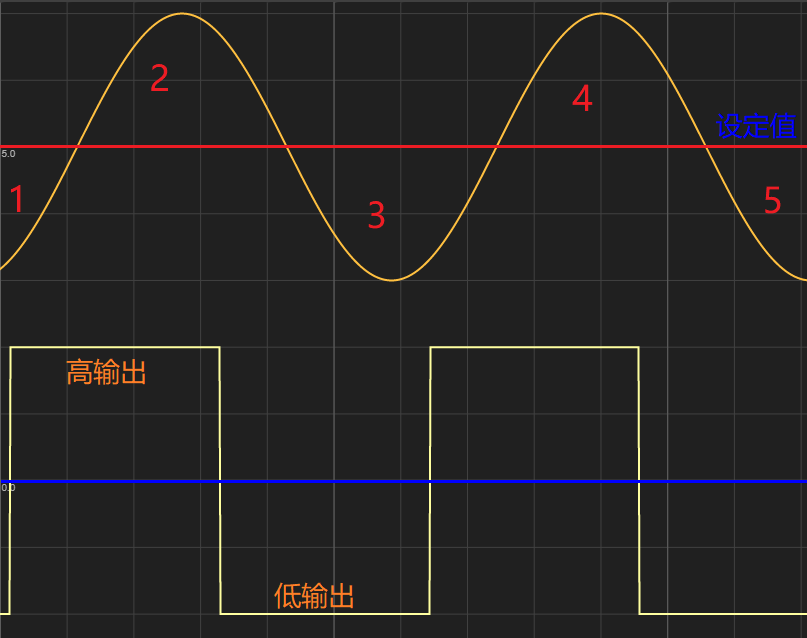
  通过上述图例我们可以知道，检测到4次已经可以有两个波形，可以确认系统已经出现了振荡。而且我们可以得到一个周期的完整且稳定的数据，即图中区域3和区域4所组成的波形周期。通过这些数据我们就可以得到振荡波形的周期Tc和振荡波形的幅值。而这些数据就是我们计算所需要的。

2.2、参数计算

  我们在上述振荡波型的测量中得到了，最大值和最小值，而波形的幅值就是最大最小差值的一半，所以我们得到了幅值A。我们将最大值几位PVmax，最小值几位PVmin就可以得到Kc的计算公式如下：
K_c=4d/πA=8d/(π*(PV_max-PV_min))
  而在测量过程中，在2次过零后我们记录了该周期的起始时间。在4次过零后我们记录了该周期的结束时间，所以我们利用结束时间与起始时间的间隔以及采样周期就可以得到振荡的周期。
T_c=(T_end-T_start )*T_s
  在上述两个公式中，Ts为整定过程中的采样周期，而d则是我们输出切换的差值，都是我们已知的数据。这样就可以根据Ziegle-Nichols公式计算对应的PID参数了。

3、算法的实现

  我们已经分析了基于继电反馈的PID参数自整定的基本算法，这一节我们将基于前述的算法分析实现它。根据前述的算法分析，我们了解到产生振荡并测量数据时，因初始偏差的正负不同而需要分辨不同状态下的处理。还有整定成功与整定不成功也会有不同的操作。

3.1、相关变量的定义

  经过前面的分析，我们知道要实现整定过程需要诸多的变量控制和记录整个整定过程。为了便于对这些变量进行管理，我们使用结构体来统一处理这些变量。经过分析我们定义整定过程控制变量结构体如下：

/*定义整定过程变量结构体类型*/
typedef struct TuneObject {
    uint8_t tuneEnable:2;       //整定与PID控制开关，0：PID控制；1：参数整定；2：整定失败
    uint8_t preEnable:2;        //预处理使能，在开始整定前置位
    uint8_t initialStatus:1;    //记录开始整定前偏差的初始状态
    uint8_t outputStatus:1;     //记录输出的初始状态，0允许上升过零计数；1允许下降过零计数
    uint8_t controllerType:2;   //控制器类型：0，P控制器；1，PI控制器；2，PID控制器
    
    uint8_t zeroAcrossCounter;  //过零点计数器，每次输出改变加1，比实际过零次数多1
    uint8_t riseLagCounter;     //上升迟滞时间计数器
    uint8_t fallLagCounter;     //下降迟滞时间计数器
    
    uint16_t tunePeriod;        //整定采样周期
    uint32_t tuneTimer;         //整定计时器
    uint32_t startTime;         //记录波形周期起始时间
    uint32_t endTime;           //记录波形周期结束时间
    
    float outputStep;           //输出阶跃d
    float maxPV;                //振荡波形中测量值的最大值
    float minPV;                //振荡波形中测量值的最小值
}TuneObjectType;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

3.2、整定的前期处理

  在前面我们已经说过了，整定开始时设定值与测量值的相对位置对过程的判断至关重要，所以在整定过程开始前我们要对其进行识别。另外在整定开始前一些控制变量也需要对其进行必要的设定，所以我们设计一个预处理的过程来完成这些前期的工作。

/*整定开始前的预处理，判断状态及初始化变量*/
static void TunePretreatment(CLASSICPID *vPID,TuneObjectType *tune)
{
    tune->maxPV=vPID->minimum;
    tune->minPV=vPID->maximum;
    tune->tuneTimer=0;
    tune->startTime=0;
    tune->endTime=0;
    tune->outputStep=100;
    
    if(*vPID->pSV>=*vPID->pPV)
    {
        tune->initialStatus=1;
        tune->outputStatus=0;
    }
    else
    {
        tune->initialStatus=0;
        tune->outputStatus=1;
    }
    
    tune->preEnable=0;
    tune->zeroAcrossCounter=0;
    tune->riseLagCounter=0;
    tune->fallLagCounter=0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

3.3、整定过程的控制

  整定过程的控制就是实现整个整定过程的各种操作。包括对输出高低转换的控制、对形成振荡后对第二个波形的数据记录、整定成功后的相关处理以及整定失败后的相关处理等。

void RelayFeedbackAutoTuning(CLASSICPID *vPID,TuneObjectType *tune)
{
    /*整定开始前的预处理，只执行一次*/
    if(tune->preEnable==1)
    {
        TunePretreatment(vPID,tune);
    }
    
    uint32_t tuneDuration=0;
    tune->tuneTimer++;
    tuneDuration=(tune->tuneTimer*tune->tunePeriod)/1000;
    if(tuneDuration>3600)       //整定过程持续超过1小时，未能形成有效振荡，整定失败
    {
        tune->tuneEnable=2;
        tune->preEnable=1;
        return;
    }
    
    if(*vPID->pSV>=*vPID->pPV)      //设定值大于测量值，则开执行单元
    {
        tune->riseLagCounter++;
        tune->fallLagCounter=0;
        
        if(tune->riseLagCounter>LAG_PHASE)
        {
            *vPID->pMV=100;
            if(tune->outputStatus==0)
            {
                tune->outputStatus=1;
                tune->zeroAcrossCounter++;
                
                if(tune->zeroAcrossCounter==3)
                {
                    tune->startTime=tune->tuneTimer;
                }
            }
        }
    }
    else                            //设定值小于测量值，则关执行单元
    {
        tune->riseLagCounter=0;
        tune->fallLagCounter++;
        
        if(tune->fallLagCounter>LAG_PHASE)
        {
            *vPID->pMV=0;
            if(tune->outputStatus==1)
            {
                tune->outputStatus=0;
                tune->zeroAcrossCounter++;
                
                if(tune->zeroAcrossCounter==3)
                {
                    tune->startTime=tune->tuneTimer;
                }
            }
        }
    }
    
    if(tune->zeroAcrossCounter==3)                  //已经两次过零，可以记录波形数据
    {
        if(tune->initialStatus==1)                  //初始设定值大于测量值，则区域3出现最小值
        {
            if(*vPID->pPV<tune->minPV)
            {
                tune->minPV=*vPID->pPV;
            }
        }
        else if(tune->initialStatus==0)             //初始设定值小于测量值，则区域3出现最大值
        {
            if(*vPID->pPV>tune->maxPV)
            {
                tune->maxPV=*vPID->pPV;
            }
        }
    }
    else if(tune->zeroAcrossCounter==4)             //已经三次过零，记录另半波的数据
    {
        if(tune->initialStatus==1)                  //初始设定值大于测量值，则区域4出现最大值
        {
            if(*vPID->pPV>tune->maxPV)
            {
                tune->maxPV=*vPID->pPV;
            }
        }
        else if(tune->initialStatus==0)             //初始设定值小于测量值，则区域4出现最小值
        {
            if(*vPID->pPV<tune->minPV)
            {
                tune->minPV=*vPID->pPV;
            }
        }
    }
    else if(tune->zeroAcrossCounter==5)             //已经四次过零，振荡已形成可以整定参数
    {
        CalculationParameters(vPID,tune);
        
        tune->tuneEnable=0;
        tune->preEnable=1;
    }  
}	
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101

3.4、参数的计算

  当整定过程实现4次过零后，说明整定成功能，这时我们需要根据我们测量到的数据计算PID参数。具体的计算公式在前面已经详细描述过了。根据公式可以实现编码如下：

/*计算PID参数值*/
static void CalculationParameters(CLASSICPID *vPID,TuneObjectType *tune)
{
    float kc=0.0;
    float tc=0.0;
    float zn[3][3]={{0.5,100000.0,0.0},{0.45,0.8,0.0},{0.6,0.5,0.125}};
    
    tc=(tune->endTime-tune->startTime)*tune->tunePeriod/1000.0;
    kc=(8.0*tune->outputStep)/(PI*(tune->maxPV-tune->minPV));
    
#if PID_PARAMETER_STYLE > (0)
    *vPID->pKp=zn[tune->controllerType][0]*kc;                                   //比例系数
    *vPID->pKi=*vPID->pKp*tune->tunePeriod/(zn[tune->controllerType][1]*tc);     //积分系数
    *vPID->pKd=*vPID->pKp*zn[tune->controllerType][2]*tc/tune->tunePeriod;       //微分系数
#else
    *vPID->pPb=100/(zn[tune->controllerType][0]*kc);                             //比例带
    *vPID->pTi=zn[tune->controllerType][1]*tc;                                   //积分时间
    *vPID->pTd=zn[tune->controllerType][2]*tc;                                   //微分时间
#endif
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

4、应用与结论

  本篇中我们设计并实现了基于一种继电反馈方法的PID参数自整定的过程。在使用中，我们需要基于整定结构体声明一个变量用于整个过程的控制。该变量定义后，成员变量tuneEnable、preEnable和controllerType需要提前赋值。tuneEnable变量值为0时是使用PID控制器，而tuneEnable变量值为1时是开启整定过程，当tuneEnable变量值为2时是指示整定失败。preEnable变量在整定前赋值为1，表示先做预处理。而controllerType则根据所整定的控制器的类型来定，主要用于参数的计算。
  使用此方法时需要注意，对于那些不允许产生波动的控制对象采用此法是不合适的。特别是一些工业现场，大幅度的波动本身就是不被允许的。但对于一些如嵌入式的小系统，简单回路的PID控制系统此法是可行的。
  此方法适用于自平衡系统对象，对于非自平衡对象将不能达到相应的效果。更多的时候不会引起有小的振荡，没有办法通过此方法得到PID参数。

欢迎关注：