算法#01--素数和牛顿迭代法求平方根_质数平方根原理

素数

1.概念

质数（prime number）又称素数，有无限个。除了1和它本身以外不再有其他的除数整除。根据算术基本定理，每一个比1大的整数，要么本身是一个质数，要么可以写成一系列质数的乘积，最小的质数是2。

2.论点

在一般领域，对正整数n，如果用2到根号n之间的所有整数去除，均无法整除，则n为质数。

3.证明

如果n不能被2到根号n之间的任一整数整除，且不是质数，那么n可以表示为：n=ab，其中ab是非1正整数。
因为n不能被2到根号n之间的任一整数整除，所以a＞根号n，b＞根号n，ab＞根号n×根号n=n。
这跟ab=n是矛盾的,所以原来的命题得证.

4.代码实现

public static boolean isPrime(int N)
{
    if(N<2) return false;
    for(int i =2; i*i<N; i++)
        if(N%i==0) return false;
    return true;
}
1
2
3
4
5
6
7

牛顿迭代法求平方根

1.概念

牛顿迭代法（Newton’s method）又称为牛顿-拉夫逊方法（Newton-Raphson method），它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。

多数方程不存在求根公式，因此求精确根非常困难，甚至不可能，从而寻找方程的近似根就显得特别重要。

方法使用函数f(x)的泰勒级数的前面几项来寻找方程f(x) = 0的根。牛顿迭代法是求方程根的重要方法之一，其最大优点是在方程f(x) = 0的单根附近具有平方收敛，而且该法还可以用来求方程的重根、复根。

2.公式

3.证明

例如，我想求根号2等于多少。假如我猜测的结果为4，虽然错的离谱，但你可以看到使用牛顿迭代法后这个值很快就趋近于根号2了：

( 4 + 2/ 4 ) / 2 = 2.25
( 2.25 + 2/ 2.25 ) / 2 = 1.56944..
( 1.56944..+ 2/1.56944..) / 2 = 1.42189..
( 1.42189..+ 2/1.42189..) / 2 = 1.41423..

证明过程如下：

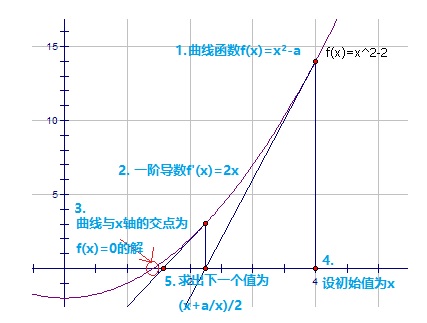
①设曲线为f(x)=x²-a。

②求出一阶导数函数为f’(x)=2x。也就是说，函数上任一点(x,f(x))处的切线斜率是2x。

③根号a实际上就是x^2-a=0的一个正实根。

④不断用(x,f(x))的切线来逼近这个根。设初始值为x。

⑤求出一阶导数函数与x轴的交点x-f(x)/(2x)，此为下一个值x，就是一个比x更接近的近似值。

那么，代入f(x)=x^2-a得到x-(x^2-a)/(2x)，也就是(x+a/x)/2。

4.代码实现

public static double sqrt(double c)
{
    if(c<0) return Double.NaN;
    double err = 1e-15;//精度
    double t = c;//赋初值
    while(Math.abs(t*t - c)>err*t)//控制迭代精度
        t = (c/t+t)/2.0;//迭代公式
    return t;
}
1
2
3
4
5
6
7
8
9

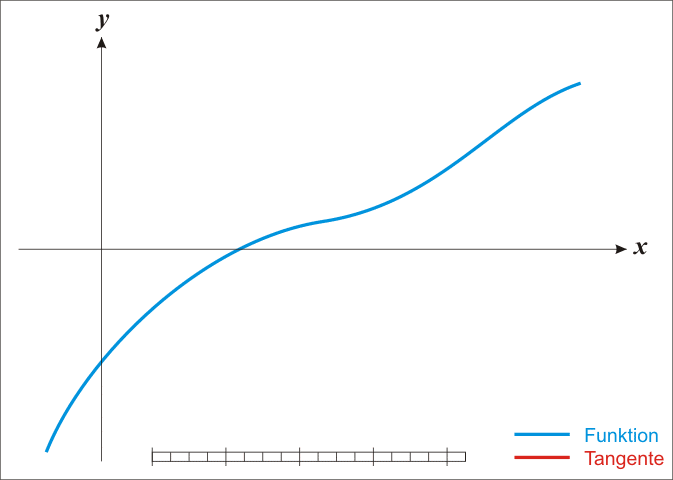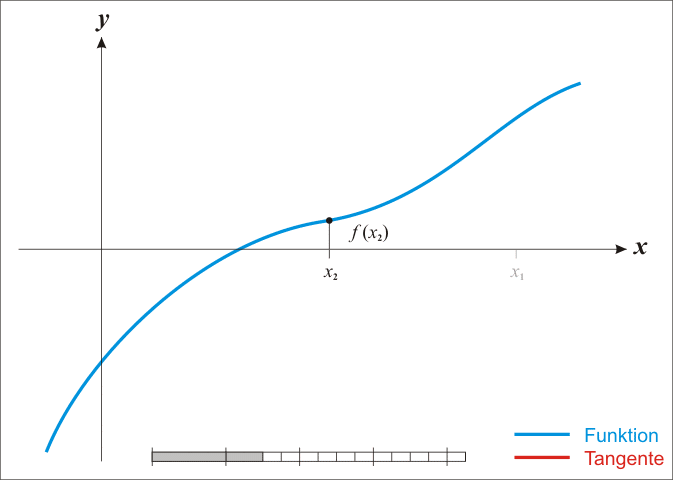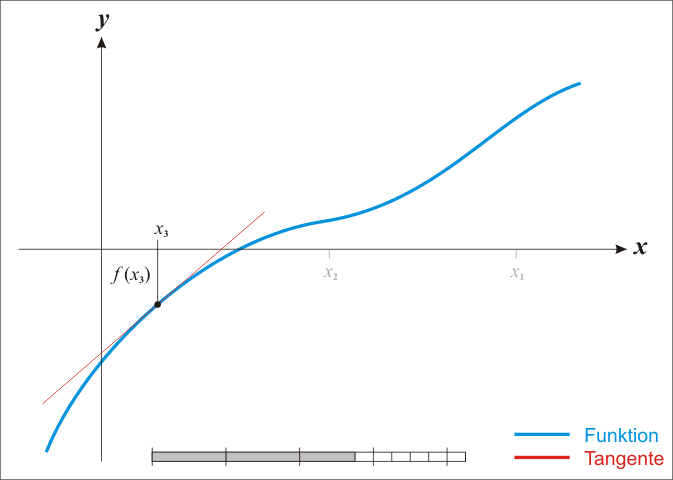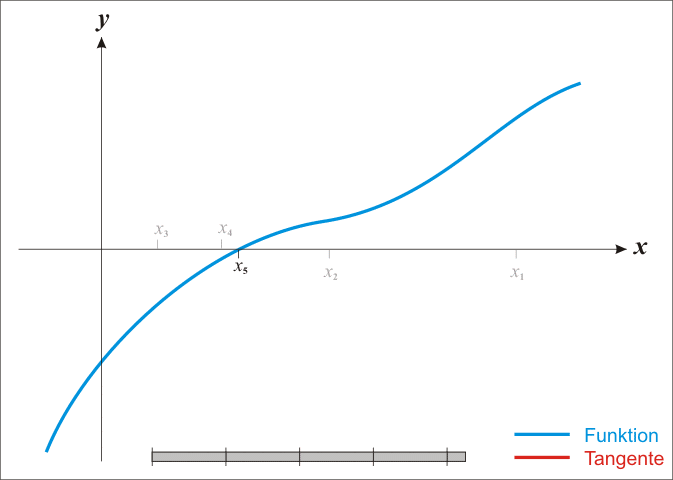
最后贴一张动态演示图：