机器学习（五） -- 监督学习（2） -- k近邻

目录

前言

一、K近邻通俗理解及定义

二、原理理解及公式

1、距离度量

四、接口实现

1、鸢尾花数据集介绍

2、API

3、流程

3.1、获取数据

3.2、数据预处理

3.3、特征工程

3.4、knn模型训练

3.5、模型评估

3.6、结果预测

4、超参数搜索-网格搜索

5、优缺点

---

前言

tips：标题前有“***”的内容为补充内容，是给好奇心重的宝宝看的，可自行跳过。文章内容被“文章内容”删除线标记的，也可以自行跳过。“！！！”一般需要特别注意或者容易出错的地方。

本系列文章是作者边学习边总结的，内容有不对的地方还请多多指正，同时本系列文章会不断完善，每篇文章不定时会有修改。

文中为方便理解，会将接口在用到的时候才导入，实际中应在文件开始统一导入。

---

一、K近邻通俗理解及定义

1、什么叫k近邻（What）

K-近邻算法（K Nearest Neighbor）又叫KNN算法。指如果一个样本在特征空间中的k个最相似（特征空间中最近邻）的样本中的大多数属于某一个类别，则该样本也属于这个类别。

（如图，我离小羽最近，所以我也属于武侯区）

2、k近邻的目的（Why）

核心思想：根据你的“邻居”的类别来推断出你的类别

（通过找到找到样本中离我们最近的K个样本，类别中样本数最多的类别就是我的类别）

3、怎么做（How）

K-近邻算法流程：

1. 计算已知类别数据集中的点（已知类别点）与当前点（待分类点）之间的距离
2. 按距离递增次序排序
3. 选取与当前点距离最小的k个点
4. 统计前k个点所在的类别出现的频率
5. 返回前k个点出现频率最高的类别作为当前点的预测分类

这里就有两个问题：K值怎么取？怎么取确定离我最近呢（怎么确定距离）？

一般手动调节K值大小：
        k 值取得过小，容易受到异常点的影响
        k 值取得过大，样本不均衡的影响

距离计算：
        欧氏距离（距离平方值）
        曼哈顿距离 （距离绝对值）
        切比雪夫距离（维度的最大值）
        明可夫斯基距离

二、原理理解及公式

1、距离度量

距离度量用于计算给定问题空间中两个对象之间的差异，即数据集中的特征。然后可以使用该距离来确定特征之间的相似性， 距离越小特征越相似；

1.1、欧氏距离（Euclidean Distance）

空间中两点间的直线距离。（一般使用方法）

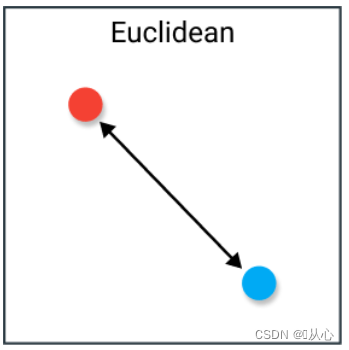
欧式距离也称为l2范数，公式：

1.2、曼哈顿距离（Manhattan Distance）

也称为城市街区距离，因为两个点之间的距离是根据一个点只能以直角移动计算的。这种距离度量通常用于离散和二元属性，这样可以获得真实的路径；

欧式距离也称为l1范数，公式： 

1.3、切比雪夫距离（Chebyshev Distance）

切比雪夫距离也称为棋盘距离，二个点之间的距离是其各坐标数值差绝对值的最大值。

欧式距离也称为l-无穷范数，公式：

1.4、闵氏距离（Minkowski）（闵可夫斯基距离）

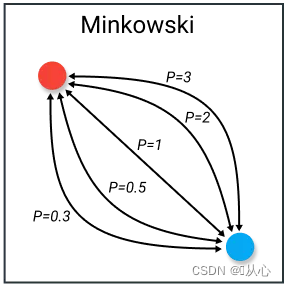
当p = 1 时，即为曼哈顿距离；
当p = 2 时，即为欧氏距离；注：只有欧式距离具有平移不变性；
当p = ∞时，即为切比雪夫距离；

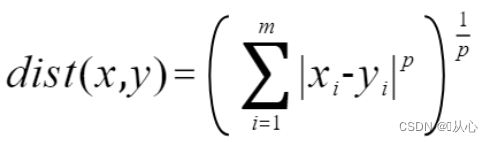
三、**算法实现

四、接口实现

1、鸢尾花数据集介绍

1.1、API

# API
from sklearn.datasets import load_iris

 1.2、介绍

 鸢尾花数据集共收集了三类鸢尾花，即Setosa鸢尾花、Versicolour鸢尾花和Virginica鸢尾花，每一类鸢尾花收集了50条样本记录，共计150条。

 数据集包括4个属性，分别为花萼的长、花萼的宽、花瓣的长和花瓣的宽。单位是cm。

iris = load_iris()
 
 
print("鸢尾花数据集的键",iris.keys())
# "数据--特征值"，"目标值"，""，"目标名"，"描述"，"特征名"，"文件名"，"数据模型名"
 
print(iris.data.shape)
 
 
print("鸢尾花数据集特征值名字是：",iris.feature_names)
# sepal length 花萼长度、sepal width 花萼宽度、petal length 花瓣长度、petal width 花瓣宽度（单位是cm）
 
print("鸢尾花数据集目标值名字是：",iris.target_names)
# Setosa（山鸢尾）、Versicolour（杂色鸢尾）、Virginica（维吉尼亚鸢尾）

 其他属性：

print("鸢尾花数据集的返回值：\n", iris)
# 返回值类型是bunch--是一个字典类型
 
# 既可以使用[]输出也可以使用.输出
print("鸢尾花数据集特征值是：",iris["data"])
# print("数据集特征值是：",iris.data)
print("鸢尾花数据集目标值是：",iris.target)
 
print("鸢尾花数据集的描述是：",iris.DESCR)

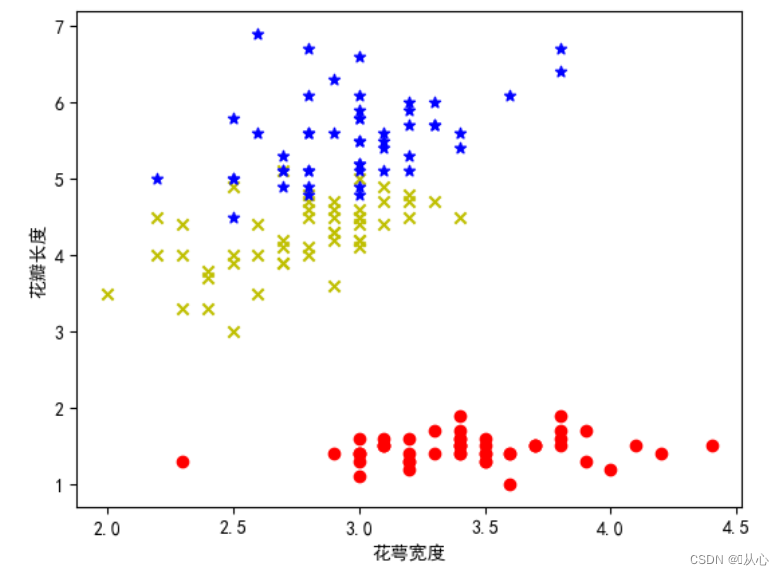
1.3、查看数据分布（两个特征）

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
np.random.seed(1734)
 
#将生成的交互式图嵌入notebook中
%matplotlib notebook 
 #将生成的静态图嵌入notebook中
%matplotlib inline
 
plt.rcParams['font.sans-serif'] = 'SimHei' # 设置字体为SimHei # 显示中文
plt.rcParams['axes.unicode_minus']=False # 修复负号问题
 
 
 
from sklearn.datasets import load_iris
 
iris = load_iris()
 
# 取150个样本，取中间两列特征，花萼宽度和花瓣长度
x=iris.data[0:150,1:3]
y=iris.target[0:150]
 
#分别取前两类样本，0和1
samples_0 = x[y==0, :]#把y=0,即Iris-setosa的样本取出来
samples_1 = x[y==1, :]#把y=1，即Iris-versicolo的样本取出来
samples_2 = x[y==2, :]#把y=2，即Iris-virginica的样本取出来
 
 
 
# 可视化
plt.figure()
plt.scatter(samples_0[:,0],samples_0[:,1],marker='o',color='r')
plt.scatter(samples_1[:,0],samples_1[:,1],marker='x',color='y')
plt.scatter(samples_2[:,0],samples_2[:,1],marker='*',color='b')
plt.xlabel('花萼宽度')
plt.ylabel('花瓣长度')
plt.show()

2、API

sklearn.neighbors.KNbeighborsClassifer
 
导入：
from sklearn.neighbors import KNeighborsClassifier
 
语法：
KNbeighborsClassifer(n_neighbors=5，algorithm='auto')
    n_neighbors:  默认为5，就是K近邻中的K值 
    Algorithm：{'auto','ball_tree','kd_tree','brute'}
        auto:可以理解为算法自己决定合适的搜索算法
        ball_tree:克服kd树高维失效而发明的，其构造过程是以质心C和半径r分割样本空间，每个节点是一个超球体。
        kd_tree:构造kd树存储数据以便对其进行快速检索的树形数据结构，kd树也就是数据结构中的二叉树。以中值切分构造的树，每个结点是一个超矩形，在维数小于20时效率高。
        brute:线性扫描，当训练集很大时，计算非常耗时

3、流程

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
 
from sklearn.neighbors import KNeighborsClassifier

3.1、获取数据

# 载入数据
iris = load_iris()
# print(iris)

3.2、数据预处理

# 划分数据集
x_train,x_test,y_train,y_test = train_test_split(iris.data, iris.target, test_size=0.2, random_state=1473) 

3.3、特征工程

进行KNN时，一般要进行无量纲化。

3.4、knn模型训练

# 实例化一个预估器
knn = KNeighborsClassifier(n_neighbors=3)
 
# 模型训练
knn.fit(x_train, y_train)

 

3.5、模型评估

# 模型评估
 
# 用模型计算测试值，得到预测值
y_pred = knn.predict(x_test)
 
# 准确率
print("预测的准确率",knn.score(x_test,y_test))
 
# 一样的哦
from sklearn.metrics import accuracy_score
print("预测的准确率",accuracy_score(y_test,y_pred))

一般用准确率就行，

# 将预测值与真实值比较
from sklearn.metrics import classification_report
print(classification_report(y_test, y_pred))

用分类报告【详情请看机器学习（四） -- 模型评估（2）-分类报告】

精确率（precision）、召回率（recall）、F1 值（F1-score）和样本数目（support）

3.6、结果预测

经过模型评估后通过的模型可以代入真实值进行预测。

4、超参数搜索-网格搜索

网格搜索法（Grid Search）是一种在机器学习中用于确定最佳模型超参数的方法之一。

超参数是指在训练模型之前需要手动设置的参数。

4.1、API：

sklearn.model_selection.GridSearchCV
 
导入:
from sklearn.model_selection import GridSearchCV
 
语法：
gs=GridSearchCV(estimator,param_grid,…,cv=’3’)
    estimator：要优化的模型对象。
    param_grid：指定参数的候选值范围，可以是一个字典或列表。
    cv：交叉验证参数，默认None，使用三折交叉验证。
 
gs.fit()：运行网格搜索
 
gs.best_estimator_：返回在交叉验证中选择的最佳估计器。
gs.best_params_：返回在交叉验证中选择的最佳参数组合。
gs.best_score_：返回在交叉验证中选择的最佳评分。
gs.cv_results_：返回一个字典，具体用法模型不同参数下交叉验证的结果。
gs.scorer_：返回用于评分的评估器。
gs.n_splits_：返回交叉验证折叠数。

4.2、实践：

# 构造参数列表
param = {"n_neighbors": [3, 5, 10, 12, 15]}
 
# 进行网格搜索，cv=3是3折交叉验证
gs = GridSearchCV(knn, param_grid=param, cv=3)
 
 
 
gs.fit(x_train, y_train)  #你给它的x_train，它又分为训练集，验证集
 
 
# 预测准确率，为了给大家看看
print("在测试集上准确率：", gs.score(x_test, y_test))
 
print("在交叉验证当中最好的结果：", gs.best_score_)
 
print("选择最好的模型是：", gs.best_estimator_)
 
print("最好的参数是 ", gs.best_params_)
 
# print("每个超参数每次交叉验证的结果：", gs.cv_results_)

 有关交叉验证移步【机器学习（四） -- 模型评估（1）】

5、优缺点

5.1、优点：

        简单，易于理解，易于实现

5.2、缺点：

1. 必须指定K值，K值选择不当则分类精度不能保证

2. 需要算每个测试点与训练集的距离，当训练集较大时，计算量相当

   大，时间复杂度高，特别是特征数量比较大的时候。
   需要大量的内存，空间复杂度高。

   懒惰算法，对测试样本分类时的计算量大，内存开销大