【前端面试3+1】17 伪类和伪元素的区别、CSS权重、图片显示优化、【二叉树最大深度】

一、伪类和伪元素的区别

1、伪类：

• 伪类是用来描述元素的特定状态的选择器，比如:hover、:active、:first-child等。
• 伪类在选择器中以冒号（:）开头，用于匹配处于特定状态的元素。
• 伪类可以用于选择DOM元素的特定状态，但并不会在文档中生成新的内容。

示例：选择第一个子元素的样式

ul li:first-child {
  color: red;
}

2、伪元素：

• 伪元素是用来在文档中生成虚拟元素的选择器，比如::before、::after等。
• 伪元素在选择器中以双冒号（::）开头，用于在元素的内容前后生成额外的样式。
• 伪元素可以用于在元素的内容前后插入额外的内容，比如添加装饰性的内容或样式。

示例：在元素的内容前插入一个装饰性的元素

p::before {
  content: "$";
}

3、小结：

伪类用于选择元素的特定状态，而伪元素用于在元素的内容前后生成虚拟元素。

二、CSS权重

CSS选择器的权重是用来确定样式优先级的重要概念，通常用于解决样式冲突的问题。CSS选择器的权重由四个部分组成，分别是：

1. 内联样式：在元素的style属性中直接设置的样式。权重值为1000。
2. ID选择器：通过#符号定义的选择器。权重值为100。
3. 类选择器、属性选择器和伪类选择器：权重值为10。
4. 元素选择器和伪元素选择器：权重值为1。

内联样式>ID选择器>类选择器、属性选择器、伪类选择器>元素选择器、伪元素选择器

        根据以上规则，可以计算出CSS选择器的权重，权重值越高的样式会优先生效。如果两个样式的权重相同，则后定义的样式会覆盖前面定义的样式。

例如：

#main-content .article p {
  color: blue;
}
 
.article p {
  color: red;
}

        第一个选择器的权重为100（ID选择器#main-content） + 10（类选择器.article） + 1（元素选择器p），总权重为111。 第二个选择器的权重为10（类选择器.article） + 1（元素选择器p），总权重为11。

因此，第一个选择器的样式会优先生效，段落文本颜色为蓝色。

三、图片显示优化有哪些方法？

1、图片格式优化

        选择合适的图片格式，如JPEG、PNG、WebP等，根据具体需求选择最适合的格式。JPEG适合照片和图像，PNG适合图形和透明效果，WebP是一种新一代的图片格式，具有更高的压缩率和更小的文件大小。

2、图片压缩

        通过压缩图片文件大小来减少加载时间，可以使用在线工具或图片编辑软件对图片进行压缩。注意在压缩过程中保持图片质量，避免影响显示效果。

3、响应式图片

        使用响应式图片技术，根据设备屏幕大小和分辨率加载不同尺寸的图片，提高页面加载速度和用户体验。可以使用srcset和sizes属性或者picture元素实现响应式图片加载。

4、懒加载

        使用懒加载技术延迟加载图片，只有当图片即将进入视口时才加载，减少页面加载时间和带宽占用。可以通过JavaScript库如LazyLoad.js实现图片懒加载。

5、图片CDN加速

        使用内容分发网络（CDN）来加速图片加载，将图片资源缓存到CDN节点，提高图片加载速度和用户体验。

6、图片预加载

        预加载页面中即将显示的图片，提前加载图片资源，避免用户看到空白或等待过程。

7、图片优化工具

        使用图片优化工具如ImageOptim、TinyPNG等，自动优化图片压缩和格式转换，提高页面性能。

四、【算法】二叉树最大深度

1、题目：

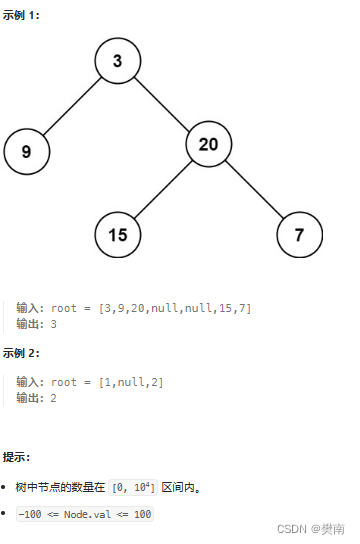
        给定一个二叉树 root ，返回其最大深度。

补充：二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数

 

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
int maxDepth(struct TreeNode* root) {
   
}

2、解题：

• 使用递归的方式计算二叉树的最大深度。
• 如果根节点为空，返回深度0。
• 否则，分别计算左子树和右子树的最大深度。
• 最大深度为1加上左子树和右子树中较大的深度。
• 递归调用直到叶子节点，然后向上返回深度值。

int maxDepth(struct TreeNode* root) {
    if (root == NULL) {
        return 0;
    } else {
        int leftDepth = maxDepth(root->left);
        int rightDepth = maxDepth(root->right);
        
        return 1 + (leftDepth > rightDepth ? leftDepth : rightDepth);
    }
}