大数据分析R中泊松回归模型实例_泊松数据分析

　　如果您知道如何以及何时使用泊松回归，它可能是一个非常有用的工具。在大数据分析R中泊松回归模型实例中，我们将深入研究泊松回归，它是什么以及R程序员如何在现实世界中使用它。

　　具体来说，我们将介绍：

　　1)泊松回归实际上是什么，什么时候应该使用它

　　2)泊松分布及其与正态分布的区别

　　3)使用GLM进行泊松回归建模4)

　　5)为计数数据建模泊松回归

　　6)使用jtools可视化来自模型的发现

　　7)为费率数据建模泊松回归

　　什么是泊松回归模型?

　　泊松回归模型最适合用于以结果为计数的事件建模。或更具体地讲， 计数数据：具有非负整数值的离散数据对某事进行计数，例如在给定时间范围内事件发生的次数或杂货店排队的人数。

　　计数数据 也可以表示为 比率数据，因为事件在时间范围内发生的次数可以表示为原始计数(即“一天，我们吃三顿饭”)或比率(“我们以每小时0.125餐”)。

　　泊松回归可以让我们确定哪些解释变量(X值)对给定的响应变量(Y值，计数或比率)产生影响，从而帮助我们分析计数数据和比率数据。例如，杂货店可以使用泊松回归来更好地了解和预测生产线中的人数。

　　什么是泊松分布?

　　泊松分布是一种以法国数学家SiméonDenis Poisson命名的统计理论。它假设在特定时间范围内发生事件y的概率 ，假设 y的 发生不受y先前发生时间的影响 。可以使用以下公式以数学方式表示：

　　

 

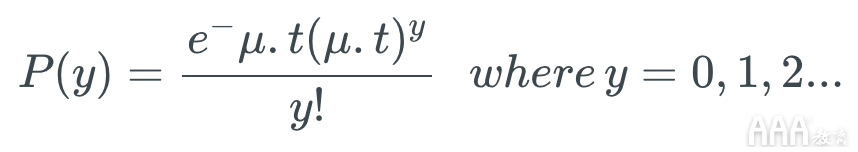
　　此处， μ (在某些教科书中，您可能会看到 λ 而不是 μ)是每单位曝光可能发生的事件的平均次数 。也称为泊松分布参数。该曝光可以是时间，空间，人口尺寸，距离或面积，但它往往是时间，与表示 吨。如果未给出曝​​光值，则假定它等于 1。

　　让我们通过为不同的μ值创建泊松分布图来形象化这一点。

　　首先，我们将创建6种颜色​​的向量：

　　

 

　　接下来，我们将为分布创建一个列表，该列表将具有不同的μ值：

　　

 

　　然后，我们将为μ创建一个值向量， 并在 每个μ的分位数范围为0-20 的值之间循环 ，并将结果存储在列表中：

　　

 

　　最后，我们将使用绘制点 plot()。 plot() 是R中的基本图形功能。在R中绘制数据的另一种常见方法是使用流行的 ggplot2 软件包。这在AAA教育的R课程中有所介绍 。但是对于大数据分析R中泊松回归模型实例，我们将坚持使用基本R函数。

　　

 

　　

 

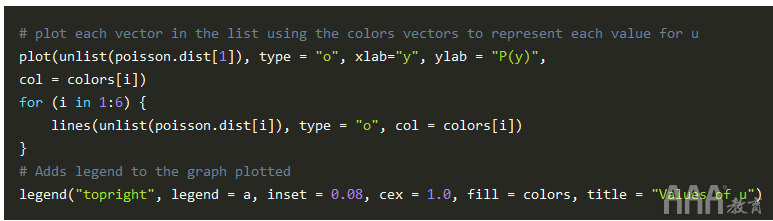
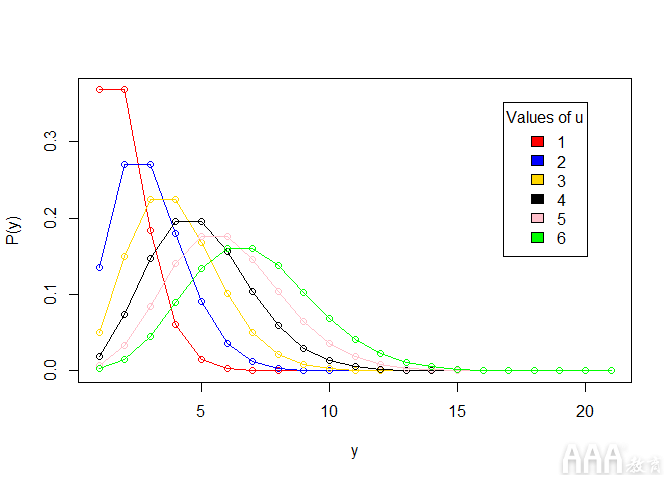
　　请注意，我们曾经dpois(sequence,lambda) 在Poisson分布中绘制概率密度函数(PDF)。在概率论中，概率密度函数是描述连续随机变量(其可能值为随机事件的连续结果的变量)具有给定值的相对可能性的函数。(在统计中，“随机”变量只是其结果是随机事件的结果的变量。)

　　泊松分布与正态分布有何不同?

　　泊松分布最常用于查找在给定时间间隔内发生事件的概率。由于我们是在讨论计数，对于Poisson分布，结果必须为0或更高–事件不可能发生负次数。另一方面，正态分布 是连续变量的连续分布，它可能导致正值或负值：

　　

 

　　我们可以在R中生成正态分布，如下所示：

　　

 

　　

 

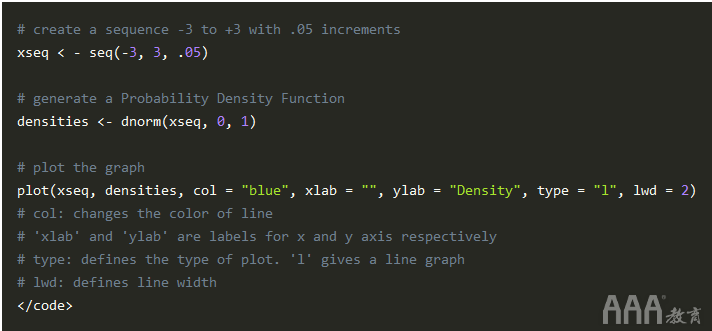
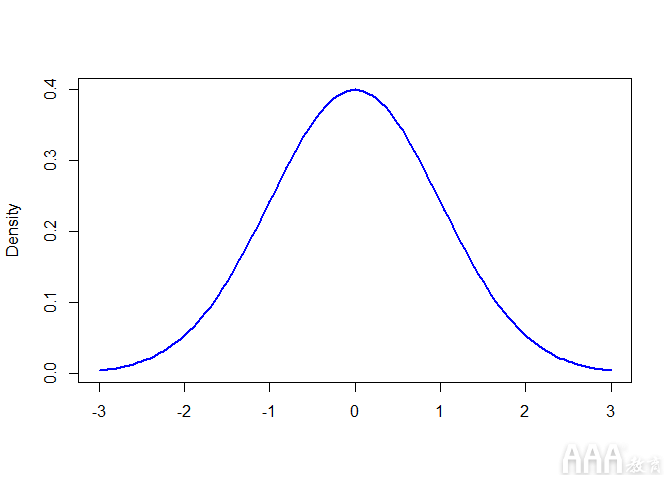
　　在R中，dnorm(sequence, mean, std.dev) 用于绘制正态分布的概率密度函数(PDF)。

　　要了解泊松分布，请从Chi Yau的R Tutorial教科书中考虑以下问题 ：

　　如果平均每分钟有12辆汽车过桥，那么在任何给定的分钟内有十七辆或更多的汽车过桥的概率是多少?

　　在这里，每分钟过桥的平均汽车数量为 μ = 12。

　　ppois(q, u, lower.tail = TRUE) 是R函数，可提供随机变量小于或等于某个值的可能性。

　　我们必须找到拥有十七 辆或更多汽车的可能性 ，因此我们将 lower.trail = FALSE q设置为16：

　　

 

　　要获得百分比，我们只需要将此输出乘以100。现在我们有了问题的答案：在任何特定分钟内，有17辆或更多的汽车过桥的可能性为10.1%。

　　泊松回归模型和GLM

　　广义线性模型是其中响应变量遵循除正态分布以外的其他分布的模型。这与线性回归模型相反，在线性回归模型中，响应变量遵循正态分布。这是因为广义线性模型具有分类的响应变量，例如“是”，“否”;或A组，B组，因此，范围从-∞到+∞。因此，响应变量和预测变量之间的关系可能不是线性的。在GLM中：

　　ÿ 我  =  α  +  β 1 X 1 我  +  β 2 X 2 我  + ... + β p X p我  +  Ê 我               我  = 1,2，...。ñ

　　响应变量 y i 由预测变量 和某些误差项的线性函数建模。

　　泊松回归模型是 广义线性模型(GLM) ，用于对计数数据和列联表建模。输出 Y (计数)是遵循泊松分布的值。它假设 可以通过一些未知参数将其建模为线性形式的期望值(均值)的对数 。

　　注意： 在统计信息中，列联表(示例)是取决于多个变量的频率矩阵。

　　要将非线性关系转换为线性形式，可以使用链接函数，该 函数 是 泊松回归的对 数。因此，泊松回归模型也称为对数线性模型。泊松回归模型的一般数学形式为：

　　升 Ô 克(Ý)= α  +  β 1 X 1  +  β 2 X 2  + ... + β p X p

　　哪里，

　　1)y：是响应变量

　　2)α 和 β：是数值系数， α 为截距，有时 α 也被表示为 β 0，它是相同的

　　3)x 是预测变量/解释变量

　　使用诸如最大似然估计(MLE)或最大拟似然之类的方法来计算系数。

　　考虑具有一个预测变量和一个响应变量的方程：

　　l o g(y)= α  +  β(x)

　　这等效于：

　　Ý  =  È (α  +  β(X))  =  È α  +  Ê β  *  X

　　注意：在Poisson回归模型中，预测变量或解释变量可以同时包含数值或分类值。

　　等分散是泊松分布和泊松回归最重要的特征 之一，这意味着分布的均值和方差相等。

　　方差度量数据的传播。它是“与均值平方差的平均值”。如果所有值都相同，则方差(Var)等于0。值之间的差异越大，方差越大。平均值是数据集的平均值。平均值是值的总和除以值的数量。

　　假设平均值(μ)表示为 E(X)

　　E(X)= μ

　　对于泊松回归，均值和方差如下：

　　v一个[R (X)= σ 2 ë(X)

　　其中 σ 2 是色散参数。由于 v一个[R (X)= È(X)(=方差平均值)必须持有泊松模型是完全适合， σ 2 必须等于1。

　　当方差大于均值时，称为 过度分散 ，并且大于1。如果小于1，则称为 欠分散。

　　使用计数数据进行泊松回归建模

　　在R中，该 glm() 命令用于对广义线性模型进行建模。这是以下内容的一般结构 glm()：

　　

 

　　在大数据分析R中泊松回归模型实例中，我们将使用这三个参数。有关更多详细信息，请查阅 R文档，但让我们快速看一下它们各自指的是什么：

　　

 

　　glm() 通过以下默认链接功能为家庭提供八个选择：

　　

 

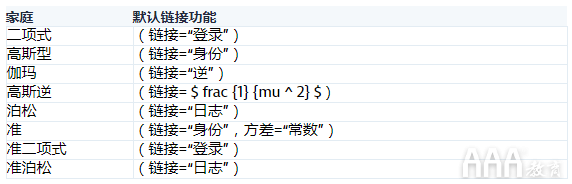
　　让我们开始建模吧!

　　我们将对与编织过程中纱线断裂的频率有关的泊松回归建模。这些数据可以datasets 在R 的包中找到 ，因此我们要做的第一件事是使用安装包install.package("datasets") 并使用 加载库 library(datasets)：

　　

 

　　该 datasets 程序包包含大量数据集，因此我们需要专门选择纱线数据。查阅软件包文档，我们可以看到它称为 warpbreaks，因此让我们将其存储为对象。

　　

 

　　让我们看一下数据：

　　

 

　　输出： [1] "breaks" "wool" "tension"

　　我们的数据中有什么?

　　该数据集查看每根固定长度的织机上不同类型的织机发生了多少经纱断裂。我们可以在此处的文档中阅读有关此数据集的更多详细信息，但是这是我们将要查看的三列以及每列所指的内容：

　　

 

　　在这六种类型的经纱中，有9种织机上都有测量值，数据集中总共有54个条目。

　　让我们看一下如何使用ls.str() 命令来构造数据：

　　

 

　　输出：

　　

 

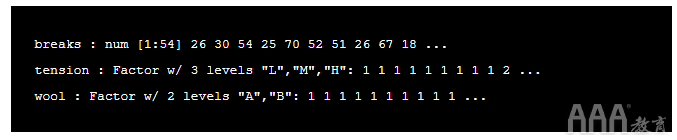
　　从上面可以看到数据中存在的类型和级别。 阅读 此书可进一步了解R中的因素。

　　现在，我们将使用 data 数据框。记住，使用泊松分布模型，我们试图找出一些预测变量如何影响响​​应变量。在这里， breaks 是响应变量 wool 和 tension 是预测变量。

　　我们可以breaks 通过创建直方图来查看因变量数据的连续性：

　　

 

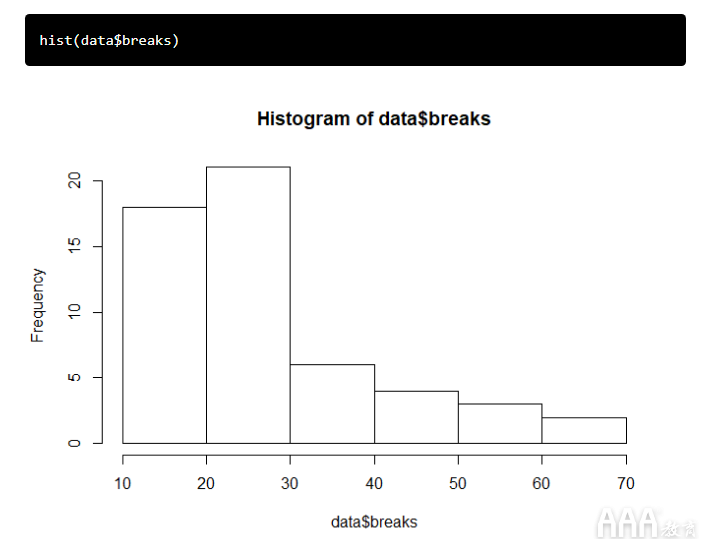
　　显然，数据不是像正态分布那样呈钟形曲线形式。

　　让我们来检查 mean() 和 var() 的因变量：

　　

 

　　输出： [1] 28.14815

　　

 

　　输出： [1] 174.2041

　　方差远大于平均值，这表明我们将在模型中出现过度分散现象。

　　让我们使用glm() 命令拟合泊松模型 。

　　

 

　　summary() 是用于生成各种模型拟合函数结果的结果摘要的通用函数。

　　

 

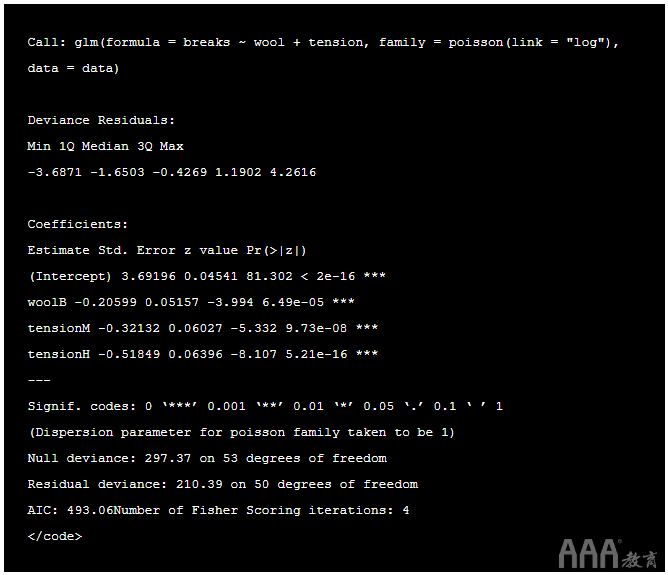
　　输出：

　　

 

　　解释泊松模型

　　我们刚刚获得了很多信息，现在我们需要对其进行解释。命名的第一列 Estimate 是的系数值 α (截距)， β 1 等。以下是参数估计的解释：

　　1)当x = 0时，e x p(α)=对均值μ的影响

　　2)È X p(β)=在X每单位增加，预测器变量具有倍增效应 ë X p(β上Y的平均值)，即 μ

　　3)如果 β = 0，则exp(β)= 1，并且预期计数为 e x p(α)，并且Y和X不相关。

　　4)如果 β > 0，则exp(β)> 1，并且预期计数是exp(β)的乘积是X = 0时的乘积

　　5)如果 β <0，则exp(β)<1，并且预期计数是exp(β)的乘积，比X = 0时小。

　　如果 family = poisson 保留， glm() 则使用最大似然估计MLE计算这些参数 。

　　R将类别变量视为伪变量。通过为变量中的级别分配一些数字表示形式，类别变量(也称为指标变量)被转换为虚拟变量。一般规则是，如果 因子变量中有 k个类别，则输出 glm() 将有 k -1个类别，其余1作为基本类别。

　　我们可以在上面的摘要中看到，对于羊毛，“ A”已成为基础，未在摘要中显示。同样，对于张力“ L”已成为基本类别。

　　要查看哪些解释变量对响应变量有影响，我们将查看 p 值。如果 p小于0.05， 则该变量会影响响应变量。在上面的总结中，我们可以看到所有的p值均小于0.05，因此， 两个 解释变量(羊毛和张力)均对休息产生重大影响。注意*** 在每个变量的末尾如何使用R输出 。星星数表示重要性。

　　在开始解释结果之前，让我们检查模型是过度分散还是分散不足。如果“ 残余偏差” 大于自由度，则存在过度分散。这意味着估算是正确的，但是标准误差(标准偏差)是错误的，模型无法解释。

　　Null偏差显示仅包含截距(均值)的模型对响应变量的预测程度，而包含自变量的模型对响应变量的预测程度。上面我们可以看到，添加了3个(53-50 = 3)自变量，将偏差从297.37降低到210.39。值之间的更大差异意味着不合适。

　　因此，要获得更正确的标准误差，我们可以使用 拟泊松 模型：

　　

 

　　输出：

　　

 

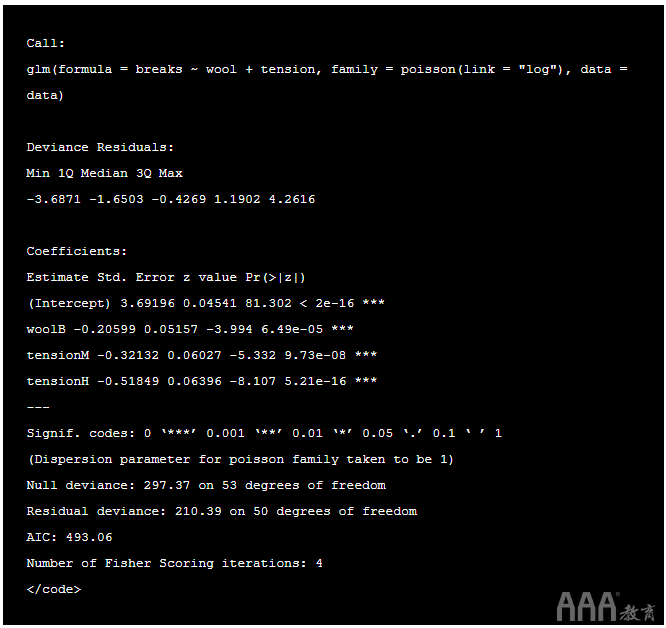
　　比较模型：

　　现在我们有了两个不同的模型，让我们比较一下它们，看看哪个更好。首先，我们将安装该arm 库，因为该 库包含我们需要的功能：

　　

 

　　现在，我们将使用该 se.coef() 函数从每个模型中提取系数，然后 cbind() 将提取的值组合到单个数据帧中，以便进行比较。

　　

 

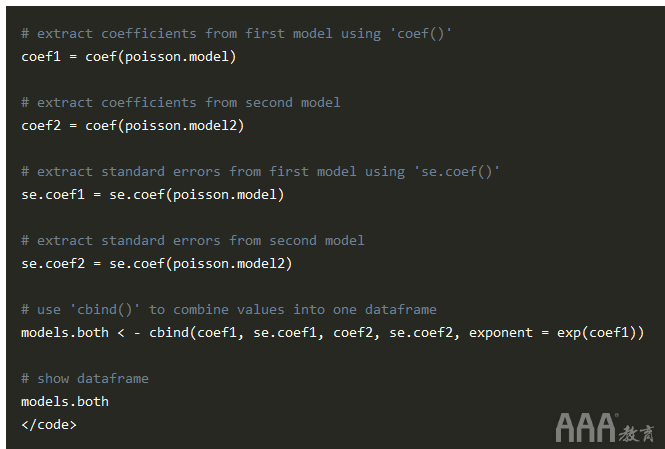
　　输出：

　　

 

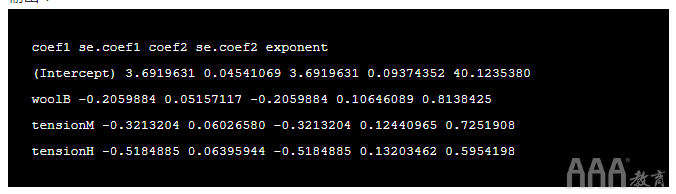
　　在上面的输出中，我们可以看到系数相同，但标准误差不同。

　　牢记这些要点，让我们来看看羊毛的估算 。它的值是 -0.2059884，并且指数 -0.2059884 是 0.8138425。

　　

 

　　输出：[1] 0.1861575

　　这表明从A型羊毛更改为B型羊毛会导致 断点 减少0.8138425 倍，因为估计值-0.2059884为负。换句话说，如果我们将羊毛类型从A更改为B，则假设所有其他变量都相同，则折断次数将减少18.6%。

　　从模型预测

　　建立模型后，我们可以使用 predict(model, data, type) 包含训练数据以外的其他数据的新数据框来预测结果。让我们来看一个例子。

　　

 

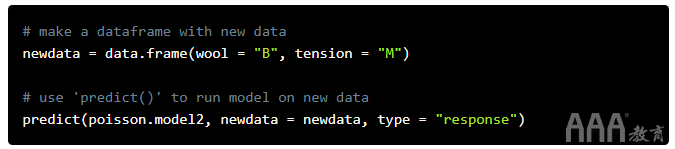
　　输出： [1] 23.68056

　　我们的模型预测， B型羊毛和M级张力的羊毛大约会断裂24次。

　　使用jtools可视化结果

　　与他人共享分析时，表格通常不是吸引人们注意力的最佳方法。图表可以帮助人们更快地掌握您的发现。在R中可视化数据的最流行的方法可能是 ggplot2 (在AAA教育的数据可视化课程中讲授 )，我们还将使用称为jtools的出色 R软件包 ，其中包括专门用于汇总和可视化回归模型的工具。让我们 jtools 来可视化 poisson.model2。

　　

 

　　jtools 提供 plot_summs() 并 plot_coefs() 可视化了模型的摘要，还允许我们与比较模型 ggplot2。

　　

 

　　

 

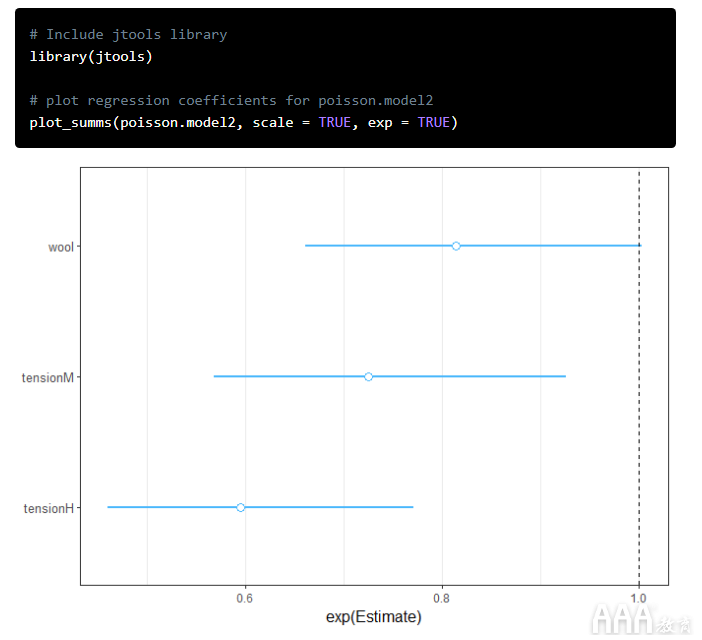
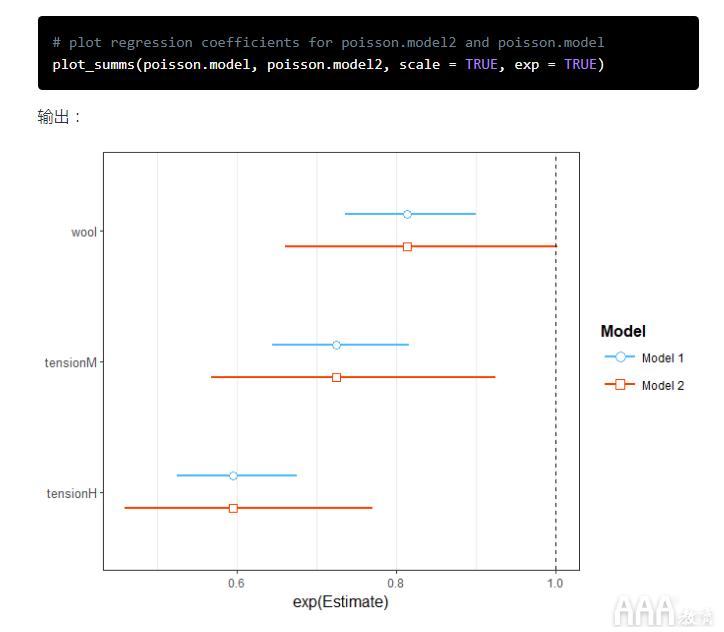
　　在上面的代码中，该plot_summs(poisson.model2, scale = TRUE, exp = TRUE) 图使用中的拟泊松族绘制了第二个模型 glm。

　　1)中的第一个参数 plot_summs() 是要使用的回归模型，它可以是一个或多个。

　　2)scale 有助于解决变量比例不同的问题。

　　3)exp 之所以设置为，TRUE是因为对于Poisson回归，我们更可能对估计的指数值感兴趣，而不是线性的。

　　你可以找到更多的细节jtools和 plot_summs() 这里的文件中。

　　我们还可以可视化预测变量之间的交互。 jtools 为不同类型的变量提供不同的功能。例如，如果所有变量都是分类变量，则可以 cat_plot() 用来更好地理解它们之间的交互。对于连续变量， interact_plot() 使用。

　　在 warpbreaks 数据中，我们具有分类的预测变量，因此，我们将使用cat_plot() 可视化变量 之间的交互作用，为其提供参数以指定我们要使用的模型，正在查看的预测变量以及其他预测变量与之结合以产生结果。

　　

 

　　输出：

　　

 

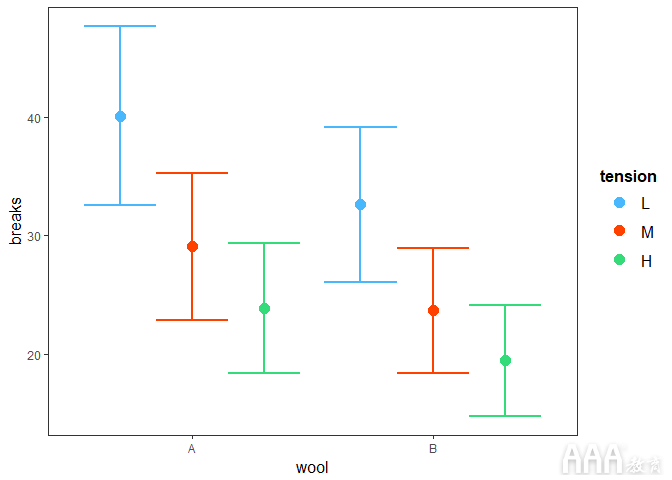
　　我们可以做同样的事情来看看tension：

　　

 

　　输出：

　　

 

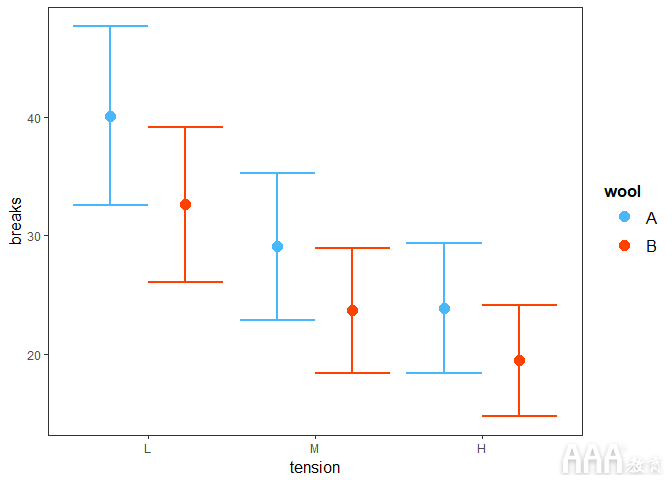
　　在上面，我们看到每种张力的三种不同类别(L，M和H)如何影响每种羊毛的断裂。例如，低张力和A型羊毛的断裂率最高。

　　我们还可以定义通过cat_plot() 使用 geom 参数创建的图的类型 。此参数增强了对图的解释。我们可以这样使用它，将其geom 作为附加参数传递 给 cat_plot：

　　

 

　　输出：

　　

 

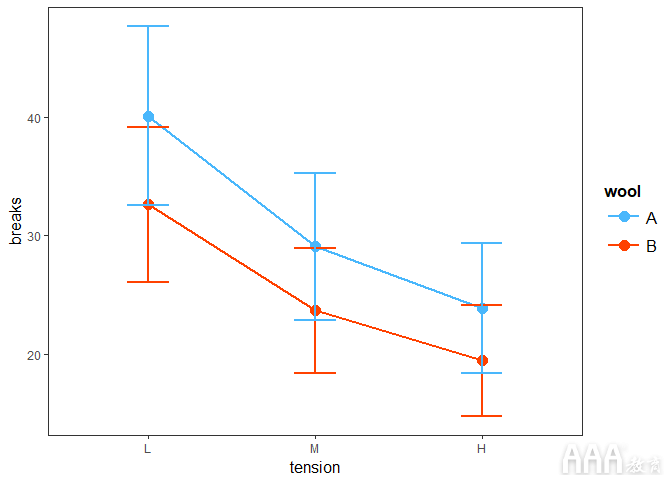
　　我们还可以通过添加plot.points = TRUE以下内容将观察结果包括在图中：

　　

 

　　输出：

　　

 

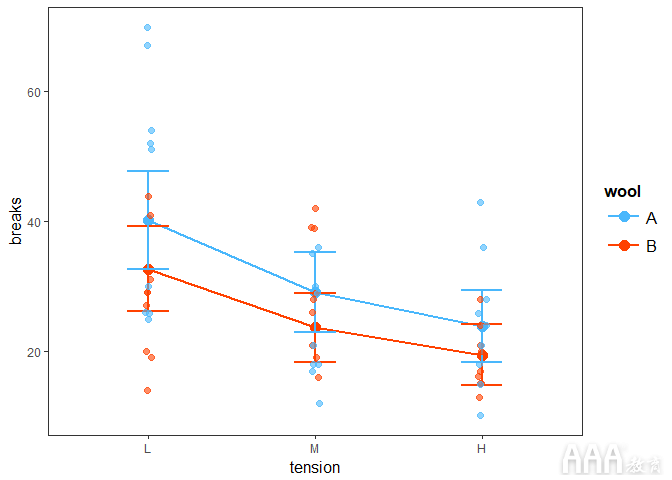
　　还有许多其他设计选项，包括线条样式，颜色等，使我们可以自定义这些可视化效果的外观。有关详细信息，请参阅此处的jtools文档 。

　　使用速率数据进行泊松回归建模

　　到目前为止，在大数据分析R中泊松回归模型实例中，我们已经对计数数据进行了建模，但是我们也可以对速率数据进行建模，该数据可以预测一段时间或分组内的计数数量。速率数据建模公式如下：

　　升 Ô 克(X / Ñ)= β 0  +Σ 我 β 我 X 我

　　这等效于：(应用对数公式)

　　升 Ô 克(X) - 升 Ö 克(Ñ)= β 0  +Σ 我 β 我 X 我

　　升 Ô 克(X)= 升 Ö 克(Ñ)+ β 0  +Σ 我 β 我 X 我

　　因此，可以通过将 系数为1 的log(n)项包括在内来对速率数据进行建模 。这称为 offset。该偏移量用offset() R 建模 。

　　让我们使用eba1977 从 ISwR包中调用的另一个数据集 为费率数据建立Poisson回归模型。首先，我们将安装该软件包：

　　

 

　　现在，让我们看一下有关数据的一些详细信息，并打印前十行以了解数据集包含的内容。

　　

 

　　输出：

　　

 

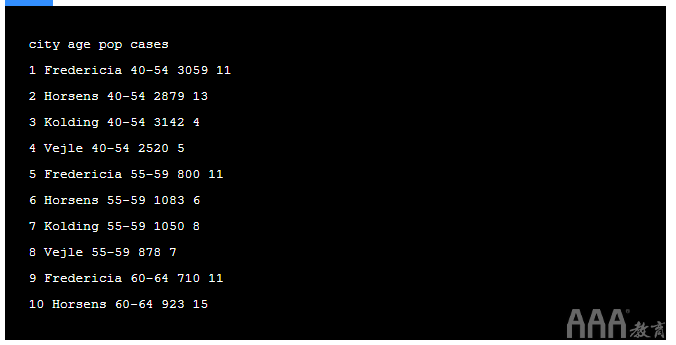
　　为了对速率数据建模，我们使用 X / n ，其中 X 是要发生的事件， n 是分组。在此示例中， X =病例 (事件是癌症病例)， n =流行病 (人群是分组)。

　　如上式所示，费率数据由 对数(n)解释，在此数据中 n 为人口，因此我们将首先找到人口的对数。我们可以为案例/人群建模， 如下所示：

　　

 

　　输出：

　　

 

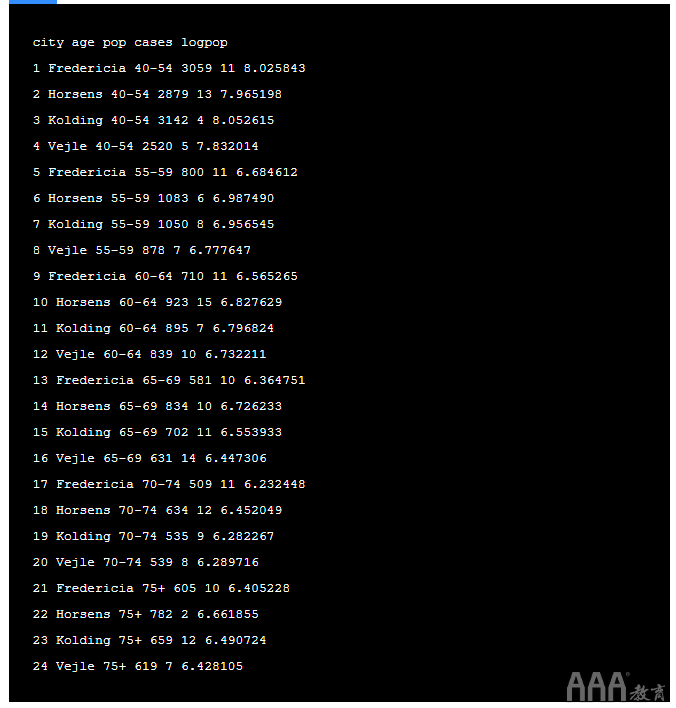
　　现在，让我们使用来对费率数据建模 offset()。

　　

 

　　输出：

　　

 

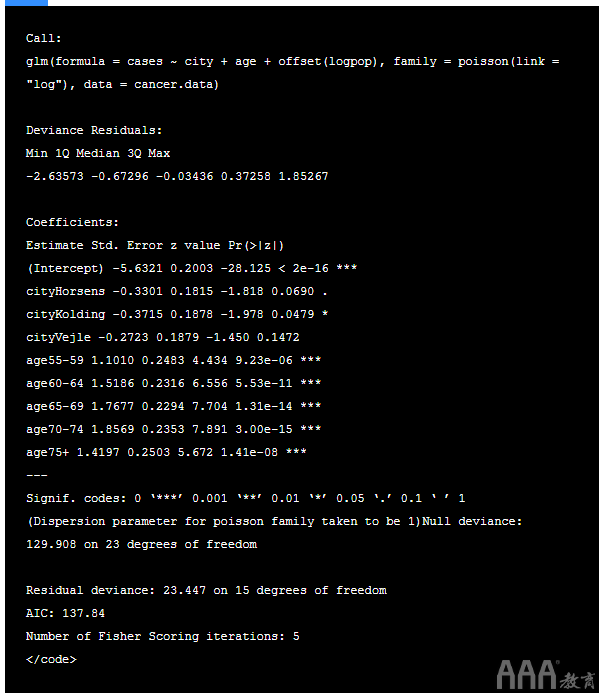
　　在此数据集中，我们可以看到残余偏差接近自由度，并且色散参数为 1.5(23.447 / 15) ，该值很小，因此该模型非常适合。

　　我们 fitted(model) 用来返回模型拟合的值。它使用建立模型的训练数据返回结果。试一试吧：

　　

 

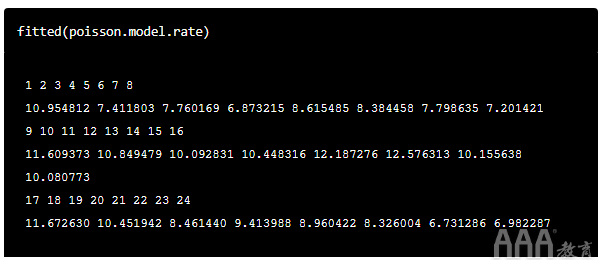
　　使用该模型，我们可以使用该predict() 函数预测新数据集每1000人口的病例数 ，就像我们之前对计数数据模型所做的那样：

　　

 

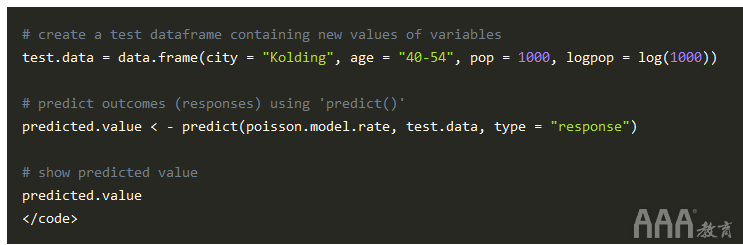
　　输出： [1] 2.469818

　　因此， 对于40-54岁年龄段人群中的科灵市，我们可以预期每千人中大约有2或3例肺癌。

　　与计数数据一样，我们也可以使用准泊松来获得速率数据的更正确的标准误差，但是出于大数据分析R中泊松回归模型实例的目的，我们将不再重复该过程。

　　结论

　　泊松回归模型在计量经济学和现实世界的预测中具有重要意义。在大数据分析R中泊松回归模型实例中，我们学习了泊松分布，广义线性模型和泊松回归模型。

　　我们还学习了如何使用来为R中的计数数据和费率数据实现泊松回归模型 glm()，以及如何将数据拟合到模型中以预测新的数据集。此外，我们研究了如何在glm()使用准泊松时获得更准确的标准误差， 并看到了一些可用于可视化的可能性 jtools。

 

摘自：https://www.aaa-cg.com.cn/data/2594.html