【多源融合】Mahony互补滤波详述_融合互补滤波

多源融合——Mahony互补滤波详述

目录

引言

传统的姿态传感器有陀螺仪、磁力计和加速度计，由于陀螺仪是一种相对测量，存在误差累积。磁力计可以绝对测量航向，加速度计则可以绝对测量俯仰角和横滚角。因此，将三种传感器结合可以提供准确的载体姿态，三者往往采用互补滤波方式进行融合。互补滤波作用面非常广，可以用于无人机、智能手机等的定姿，但是目前相关博文介绍多从无人机视角出发，对于传统测绘学生来说具有一定的障碍。因此，本文主要结合智能手机端matlab相关代码介绍博主对于Mahony滤波的理解。

基础知识

在表示由载体坐标系（body frame，b系）到导航坐标系（navigation frame，n系）时常见的物理量有欧拉角、方向余弦矩阵和四元数，这里我们主要介绍四元数方法。
四元数q是由一个实部和三个虚部共四个元素组成的四维数组，表示为（为了简洁，q均采用q代替，具有数字的则为对应元素）
q = [ q 1 q 2 q 3 q 4 ] = = q 0 + q 1 i + q 2 j + q 3 j + q 4 k = q 0 + q v q=\left[

$$\begin{matrix} q_1\\ q_2\\ q_3\\ q_4\\ \end{matrix}$$ \right]==q_0+q_1i+q_2j+q_3j+q_4k=q_0+q_v q= ​q1​q2​q3​q4​​ ​==q0​+q1​i+q2​j+q3​j+q4​k=q0​+qv​
其中，$q_1$为实部，$q_2到q_4$为虚部（$q_v$），并且定义
$$\begin{gathered} i\otimes i=-1，j\otimes j=-1，k\otimes k=-1 \\ i\otimes j=k，j\otimes i=-k，k\otimes j=-i \\ i\otimes k=-j，j\otimes k=i，k\otimes i=j \\ 1\otimes i=i\otimes 1=i，1\otimes j=j\otimes 1=j，1\otimes k=k\otimes 1=k \end{gathered}$$
并且以矩阵形式定义四元数乘$p\otimes q$
$$p\otimes q=\left[\begin{array}{cccc}{p}_1& -p_2& -p_3& -p_4\\ p_2& p_1& -p_4& p_3\\ p_3& p_4& p_1& -p_2\\ p_4& -p_3& p_2& p_1\end{array}\right]\left[\begin{array}{c}{q}_1\\ q_2\\ q_3\\ q_4\end{array}\right]$$
或
$$p\otimes q=\left[\begin{array}{cccc}{q}_1& -q_2& -q_3& -q_4\\ q_2& q_1& q_4& -q_3\\ q_3& -q_4& q_1& q_2\\ q_4& q_3& -q_2& q_1\end{array}\right]\left[\begin{array}{c}{p}_1\\ p_2\\ p_3\\ p_4\end{array}\right]$$
此外，对于任意单位四元数都有
$q=q_0+q_v=\cos (\frac{\theta }{2})+u\sin (\frac{\theta }{2})$
对于任意三维向量v，算子
$L_q(v)=q\otimes v\otimes q^{\ast }$
的作用等效于使向量v绕向量u的正方向旋转角度$\theta$，$q^{\ast }$为共轭四元数，即实部不变，虚部取负号。
最后，我们定义b系右前上，n系东北天，$q_b^n$则代表由b系到n系的四元数，为方便起见，用q代替$q_b^n$。

原理与代码实现

我们以http://www.x-io.co.uk/node/8#open_source_ahrs_and_imu_algorithms网站发布的Mahony代码为例进行原理介绍，下面介绍Mahony代码的流程。
（1）利用GetSensorData读取手机AHRS姿态，转为四元数。

（2）预测当前时刻四元数。
$\dot{q}=\frac{1}{2}{\hat{q}}_{k-1}{W}_k$
$q_k^{-}={\hat{q}}_{k-1}+\dot{q}\ast \delta t$
其中，$q_k^{-}$和${\hat{q}}_{k-1}$代表历元k和k-1时的先验状态和后验状态，$W_k$则为陀螺仪观测值。

（3）标准化加速度计和磁力计数据。
该步的目的：（1）为了降低噪声的影响，因为都涉及到寻找方向的比例关系，可以近似忽略较小数值的影响；（忘了是在哪篇论文里看过了，欢迎补充）（2）为步骤（5）统一量纲，并得到近似误差。

（4）描述重力加速度和磁场方向。
需要注意的是：（a）楼主在北半球，磁场方向由南指向北，则在n系下对应 b(3) 和 b(4) 有数值，东方向近似为0，并且 b(4) 小于0。（b）加速度计获取的是包含重力加速度的加速度数值，则静止状态下只存在天向的+9.81m/s^2，归一化后为[0, 0, 1]。（c）在第（5）步中要与归一化后的加速度计和磁力计数据进行对比，所以此时的v和w为近似的磁场观测值b和加速度计读数在b系下的观测值（即将观测值b等从载体系转到导航系）。

（5）计算外积。
向量外积公式$a\times v=|a||v|\sin \theta$，当a和v均为单位向量时，外积结果近似为姿态误差，姿态误差是两种传感器数据外积之和。

（6）补偿，其中Kp和Ki是调节参数，调节这两个参数对最终定位精度影响较大，类似于PDI控制器（比例-积分控制器），对于这方面了解太少，具体含义不太清楚，能用就好。

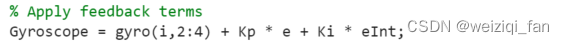
（7）计算最终四元数结果${\hat{q}}_k$

至此，Mahony算法流程介绍完毕，上述步骤中（4）-（6）就是互补滤波实现三种传感器融合的关键，将地球有关向量，如磁场向量、重力向量在磁力计和加速度计中的理论观测值转到b系下，与实际磁力计和加速度计观测值求差再进行补偿，补充了陀螺仪相对测量的不足。

参考文献

1、源码：http://www.x-io.co.uk/node/8#open_source_ahrs_and_imu_algorithms
2、武汉大学牛小骥老师惯导课程：https://space.bilibili.com/521626836?spm_id_from=333.337.search-card.all.click