面试必会：二叉搜索树（二叉排序树）构建、插入、验证详细图解，奶奶都看懂了，附二叉搜索树的二种验证方法python代码_二叉树搜索实践示意图

1、二叉排序树（Binary Sort Tree）性质：

或是一颗空树，或是具有如下性质的二叉树：

(1) 若它的左子树不空，则 左子树 上所有结点的值 均小于 它的根结点的值；

(2) 若它的右子树不空，则 右子树 上所有结点的值 均大于 它的根结点的值；

(3) 它的 左、右子树又分别为二叉排序树 。

重要性质：

1、二叉排序树的中序遍历输出一定是一个单调递增的序列。
2、二叉排序树查找指定数值相当于是一个二分查找。

2、二叉排序树举例：

下图中的这颗二叉树就是一颗典型的二叉排序树：

二叉排序树既然是名字当中带有 排序 二字，这就是它相对于普通二叉树的优势所在。

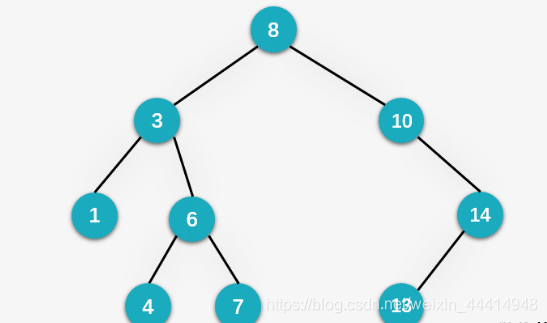
二叉排序树的每个节点上下边界如下图所示，构建、插入均是通过该边界条件判断插入位置：

3、二叉排序树构建、插入规则举例：

假设我们初始时有如下 无序序列：

第一步：插入 8 作为根结点。

第二步：插入 3 ，与根结点 8 进行比较，发现比8小，且根结点没有左孩子，则将 3 插入到 8 的左孩子。

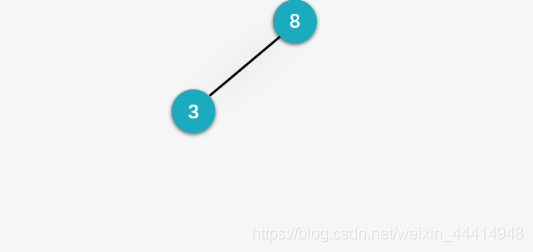
第三步：插入10，首先与根结点比较，发现比 8 大，则要将 10 插入根结点的右子树；根结点 8 的右子树为空，则将 10 作为 8 的右孩子。

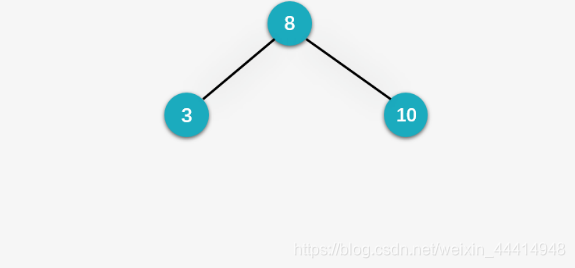
第四步：插入 1，首先与根结点比较，比根结点小，则应插入根结点的左子树。再与根结点的左孩子 3 比较，发现比 3 还小，则应插入 3 的左孩子。

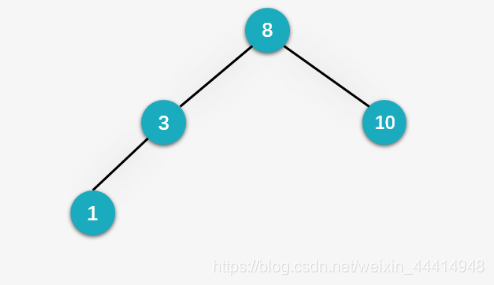
第五步：插入 6，先与根结点8比较，小于 8，向左走；再与 3 比较，大于 3，向有走，没有结点，则将6 作为3的右孩子。

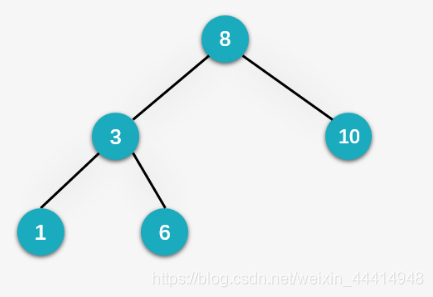
第六步：插入14，先与8比较，比 8 大，向右走；再与8的右孩子10比较，比10大，向右走，没有结点，则将14作为10的右孩子。

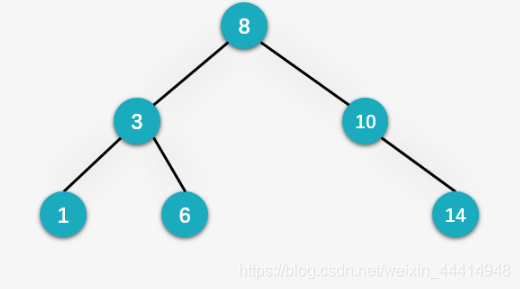
第七步：插入4，先与8比较，发现比8小，向左走，再与3比较，比3大向右走，再与6比较，向左走且没有左孩子，将4作为6的左孩子。

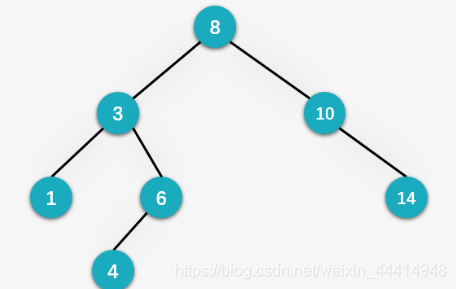
第八步：插入7，先与8比较，发现比8小，向左走，再与3比较，向右走，在与6比较，继续向右走，发现6没有右孩子，则将7作为 6的右孩子插入。

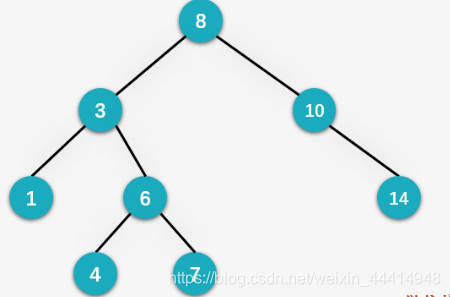
第九步：插入13，先与8比较（大于）向右，再与10比较（大于）向右，再与14比较（小于）向左，发现14的左孩子为空，则将13插入到14的左孩子位置。

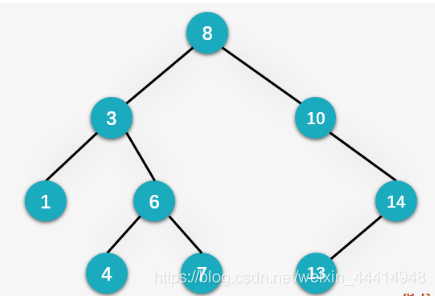
4、中序遍历结果：

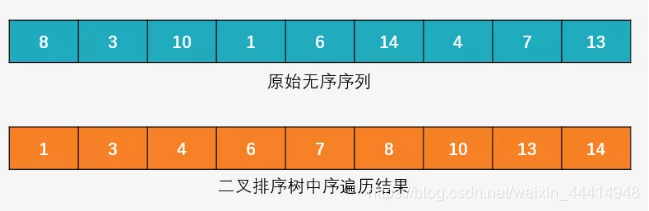
5、验证方法

（1）中序遍历验证（二叉搜索树的中序遍历一定是单调递增的数列）

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

class Solution:
    def isValidBST(self, root: TreeNode) -> bool:
        def recur(root: TreeNode)->[]:
            return recur(root.left)+[root.val]+recur(root.right) if root else []
        res = recur(root)
        return all(res[i]>res[i-1] for i in range(1, len(res)))
1
2
3
4
5
6
7
8
9
10
11
12
13

（2）构建规则验证（利用每个节点的上下界来判断是否是搜索树）

class Solution:
    def isValidBST(self, root: TreeNode) -> bool:
        return self.dg(root,-(2**32),2**32) #这里我直接粗暴地将最小值和最大值设置为一个足够小（大）的数，你可以设置你认为的最优解

    def dg(self, root, min_v, max_v): 
        # 参数：root：当前节点，min_v：允许最小值（下界），max_v：允许最大值（上界）
        if not root:
            return True
        # 同时满足所有条件才是二叉搜索树：
        # 1、当前节点root.val在上下界范围内；2、当前节点的左孩子是二叉搜索树；3、当前节点的右孩子是二叉搜索树
        if min_v<root.val<max_v and self.dg(root.left, min_v, root.val) and self.dg(root.right, root.val, max_v):
            return True
        return False
1
2
3
4
5
6
7
8
9
10
11
12
13

附：每个节点的上下界范围，省得各位姥爷往上翻了

参考：https://mp.weixin.qq.com/s?src=11&timestamp=1615380866&ver=2938&signature=8Vqt71mnf4s4sH4mKnIY-H**bGOVfI5tO7wE6tHrY50itCrUPivDcnawzzDzXyKFCmUKZm5NlZh3eAPSzstsweXsihqazkNxniSXIM9w8bCmKOhY32PiCXlM*MwxRh&new=1