梯度下降法浅思_局部最优点的函数为0则为全局最优点

梯度下降法：

已一元二次为例，保证该函数是凸函数（凸函数即局部最优点一定是全局最优点）

这样一个函数 f(x),我们想求得 f(x)=0 的解。

给定一个初值 $x_{0}$ ,找出此点的梯度方向，沿着梯度的反方向一步步走下去，当走到 $x_{7}$ 时，梯度已经趋于0，我们便找到了解。

但实际上我们求得的梯度是有大小的，很容易走的步子太大或太小，为了便于控制，我们将梯度单位化，只保留方向。

$d^{k}=-grad(x^{k})/norm(grad)$  ，norm是求出它的值  （例子 (-4/4=-1）这样便只保留了方向，然后我们再给它加上一个步长

step.这时候每次走的长度就可以控制了。

算法过程：

1. 给定初值 x，误差err, 步长
2. $d^{k}=-grad(x^{k})/norm(grad)$
3. $x^{k+1}=x^{k}+step*d^{k}$
4. 如果norm(grad)<err了，$x^{k+1}$就是解，否则继续。

 

 

用梯度下降法求函数f（x）=0

f(x)是一个函数的话，那么找到解，这个解的梯度应当为0，可是我用梯度小于误差err作为循环终止条件时，却总得不到 正确结果，想了想，可能总是得到了局部最优解了。

例子：f(x)=x*e^(x),q求f(x)=0;

​
clear all;clc;
x=[5]';err=0.000005;learn=0.0004;
    grad=g(x);
    %while(f(x)>err)
  while(norm(grad)>err)
        x=x-learn*(grad/norm(grad))
        grad=g(x);
    end
function[gx]=g(x)
    n=length(x);
    dt=1e-8;
    I=eye(n);
    fx=f(x);
    for i=1:n
        gx(i)=(f(x+dt*I(:,i))-fx)/dt;
    end
    gx=gx(:);
end
function[fx]=f(x)
    fx=x*exp(x)-1;
end

得到的结果：

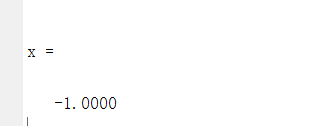
很明显不对，画图看看。可以看到在x=-1是梯度的确趋于0，但是真正的解却在0.5左右。

我们再用 f(x)>err作为终止条件

此时得到一个近似解，与图中相符合。

而当 f(x)=x1+x2^2-7时，整个程序更是停不下来，原因是有一个梯度始终为 1，所以我觉得终止条件还是 f(x)>err好一点

但是如果误差设置的小而最小值却高于误差，那么程序便不会终止。

 

所以梯度下降法使用的函数一定要是凸函数，便可以用 where(norm(grad)>err)了。

附上完善的代码：

clear all;clc;
x=[1,1]';%初始化x
err=input('误差,err=');%所要求的误差
step=input('步长,step=');%步长
cnt=0;
grad=g(x);%g(x)是在点x处的梯度
    while(norm(grad)>err)
        x=x-step*(grad/norm(grad));
        grad=g(x);
        cnt=cnt+1;
    end
disp('解');x
disp('迭代次数');cnt
function[gx]=g(x)%g(x)函数求在x处的梯度
    n=length(x);% x变量的个数
    dt=1e-8;
    I=eye(n);
    fx=f(x);
    for i=1:n
        gx(i)=(f(x+dt*I(:,i))-fx)/dt;
    end
    gx=gx(:);
end
function[fx]=f(x)%f(x)函数
    fx=x(1)-x(2)+2*x(1)*x(1)+2*x(1)*x(2)+x(2)*x(2);
end