FFTW的使用方法 - 实数输入的数字滤波示例_fftw使用

---

前言

本文主要记录FFTW的安装过程，FFTW的简单示例代码。并实现一个输入和输出为一维实数的数字滤波器

FFT的一些理论知识可以参考：
从头到尾彻底理解傅里叶变换算法
傅里叶分析之掐死教程（完整版）

一、滤波效果

先展示效果。如图一为滤波前后时域波形对比，经过低通滤波后，波形变的比较平滑。

滤除了10kHz以上的高频，以下为滤波前后频域波形对比。


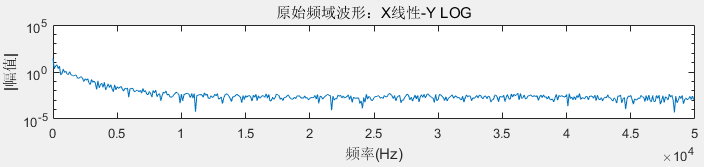
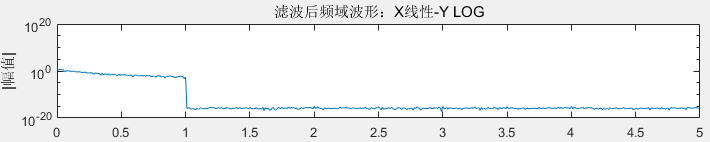
接下来是使用FFTW使用滤波的具体步骤。

---

二、下载、安装FFTW

FFTW官网下载源码 http://www.fftw.org/download.html

我是用在linux系统下，下载tar包，并解压

tar -zxvf ./fftw-3.3.10.tar.gz
cd ./fftw-3.3.10/

进行安装。一般使用默认配置安装即可（默认不使能多线程库、实数为double类型），只需如下3步
若要定制化修改配置可参考官方的 配置说明文档

./configure
make
make install

默认会安装到 /usr/local 路径下，其中 /usr/local/include放置头文件，/usr/local/lib放置.a文件

FFTW安装完成，可直接在编译时链接。

---

三、 FFTW简单示例代码

一维复数的FFT及IFFT

贴上官方给出的示例，IFFT的只需把fftw_plan_dft_1d()函数的FFTW_FORWARD改为FFTW_BACKWARD

#include <fftw3.h>
...
{
    fftw_complex *in, *out;
    fftw_plan p;
    ...
    in = (fftw_complex*) fftw_malloc(sizeof(fftw_complex) * N);
    out = (fftw_complex*) fftw_malloc(sizeof(fftw_complex) * N);
    p = fftw_plan_dft_1d(N, in, out, FFTW_FORWARD, FFTW_ESTIMATE);
    ...
    fftw_execute(p); /* repeat as needed */
    ...
    fftw_destroy_plan(p);
    fftw_free(in); fftw_free(out);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

一维实数的FFT及IFFT

一维实数的FFT和IFFT写在一起，为了更好理解功能。实际上转换前后的数据基本（近似）相同

#include <fftw3.h>
void fft_real_f(int n, const float *in, float *out)
{
    int i, begin, end;
    double *real;
    fftw_complex *complex;
    fftw_plan plan;

    // fftw的内存分配方式和mallco类似，但使用SIMD（单指令多数据流）时，fftw_alloc会将数组以更高效的方式对齐
    real = fftw_alloc_real(n);
    complex = fftw_alloc_complex(n/2+1);    // 实际只会用到(n/2)+1个complex对象

    // Step1：FFT实现时域到频域的转换
    plan = fftw_plan_dft_r2c_1d(n, real, complex, FFTW_ESTIMATE);
    for (i = 0; i < n; i++)
    {
        real[i] = in[i];
    }

    // 对长度为n的实数进行FFT，输出的长度为(n/2)-1的复数
    fftw_execute(plan);
    fftw_destroy_plan(plan);

    // Step3：IFFT实现频域到时域的转换
    // 使用FFTW_ESTIMATE构建plan不会破坏输入数据
    plan = fftw_plan_dft_c2r_1d(n, complex, real, FFTW_ESTIMATE);

    fftw_execute(plan);
    fftw_destroy_plan(plan);

    for (i = 0; i < n; i++)
    {
        // 需除以数据个数，得到滤波后的实数
        out[i] = real[i] / n;
    }

    fftw_free(real);
    fftw_free(complex);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

GCC编译

使用GCC编译是命令如下

gcc fft.c -lfftw3 -lm

四. 实现数字滤波器

接下来是实际FFT的应用，实现一个数字滤波器

/**
 * @Description : 使用FFT进行滤波
 *                使用示例：
 *                  原始采样频率为100kHz，采集了10000个点，保存为单精度浮点数。滤除其中20kHz~30kHz的频率
 *                  fft_filter_f(10000, in, out, 100e3, 20e3, 30e3)
 * @Input       : n             输入数据个数
 *                in            输入数据
 *                              in和out指向不同位置，不改变输入
 *                              in和out指向相同位置，输出将覆盖输入
 *                sample_rate   原始数据采样频率 Hz
 *                freq_start    需过滤的起始频率 Hz
 *                freq_end      需过滤的截止频率 Hz
 *                              若freq_end大于采样频率的50%，则将滤除大于freq_start的所有高频信号
 * @Output      : out           输出数据
 *                              in和out指向不同位置，不改变输入
 *                              in和out指向相同位置，输出将覆盖输入
 * @Return      : 无
*/
void fft_filter_f(int n, const float *in, float *out, float sample_rate, float freq_start, float freq_end)
{
    int i, begin, end;
    double *real;
    fftw_complex *complex;
    fftw_plan plan;

    // fftw的内存分配方式和mallco类似，但使用SIMD（单指令多数据流）时，fftw_alloc会将数组以更高效的方式对齐
    real = fftw_alloc_real(n);
    complex = fftw_alloc_complex(n/2+1);    // 实际只会用到(n/2)+1个complex对象

    // Step1：FFT实现时域到频域的转换
    plan = fftw_plan_dft_r2c_1d(n, real, complex, FFTW_ESTIMATE);
    for (i = 0; i < n; i++)
    {
        real[i] = in[i];
    }

    // 对长度为n的实数进行FFT，输出的长度为(n/2)-1的复数
    fftw_execute(plan);
    fftw_destroy_plan(plan);

    // Step2：计算需滤波的频率在频域数组中的下标
    begin = (int)((freq_start / sample_rate) * n);
    end = (int)((freq_end / sample_rate) * n);
    end = end < (n / 2 + 1) ? end : (n / 2 + 1);
    for (i = begin; i < end; i++)
    {
        // 对应的频率分量置为0，即去除该频率
        complex[i][0] = 0;
        complex[i][1] = 0;
    }
    
    // Step3：IFFT实现频域到时域的转换
    // 使用FFTW_ESTIMATE构建plan不会破坏输入数据
    plan = fftw_plan_dft_c2r_1d(n, complex, real, FFTW_ESTIMATE);

    fftw_execute(plan);
    fftw_destroy_plan(plan);

    // Step4：计算滤波后的时域值
    for (i = 0; i < n; i++)
    {
        // 需除以数据个数，得到滤波后的实数
        out[i] = real[i] / n;
    }

    fftw_free(real);
    fftw_free(complex);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68

---