数学建模国赛/美赛常见赛题类型及建模方案（纯干货）_数模国赛预测类问题题目

目录

 一，评价类问题

1，建模步骤如下图所示：

2，主客观评价问题的区别

3，如何选择合适的评价方法

 二，预测类赛题

1，预测类赛题的基本解题步骤

2，预测类问题的区别

3，如何选择合适的预测方法

三，优化类赛题

1，优化类赛题的基本解题步骤

 2，如何选择合适的优化方法

总体来说，数学建模赛题类型主要分为:评价类、预测类和优化类三种，其中优化类是最常见的赛
题类型，几乎每年的地区赛或国赛美赛等均有出题，必须要掌握并且熟悉。

如下表所示：主要分为评价类，预测类和优化类问题。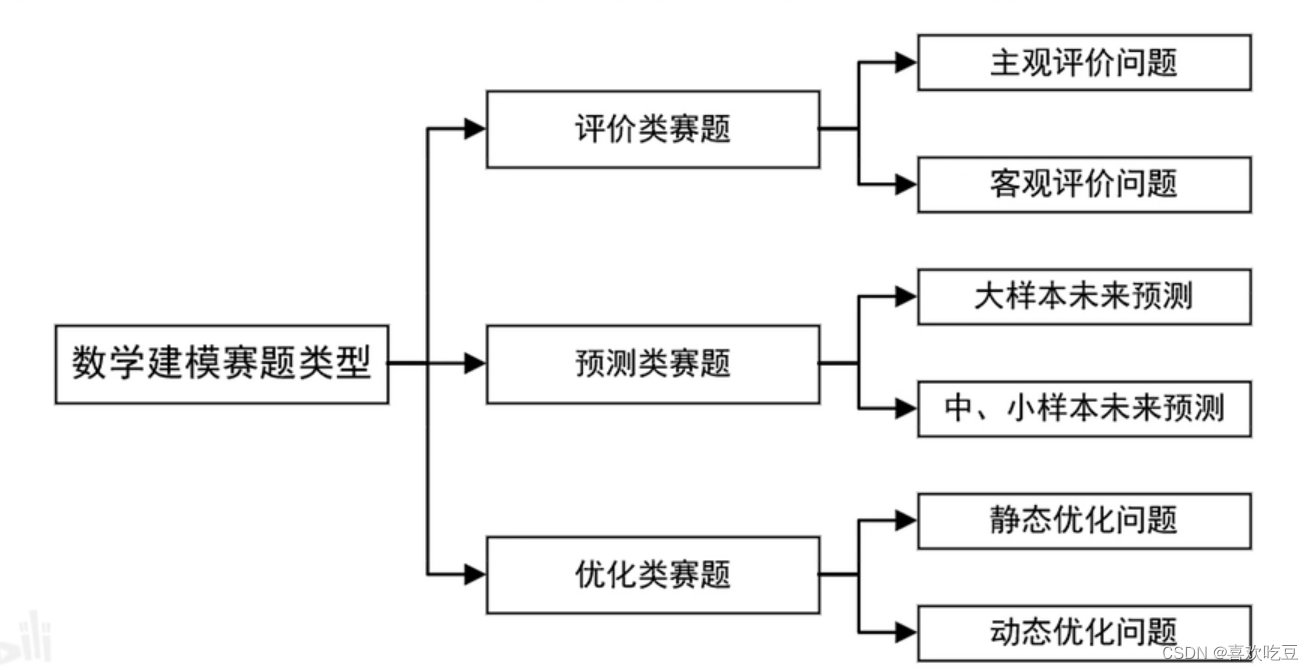

 一，评价类问题

综合评价问题是数学建模问题中思路相对清晰的一类题目，从每学期的综合测评、旅游景点的选择到挑选手机，评价类问题在生活中也是处处存在。

1，建模步骤如下图所示：

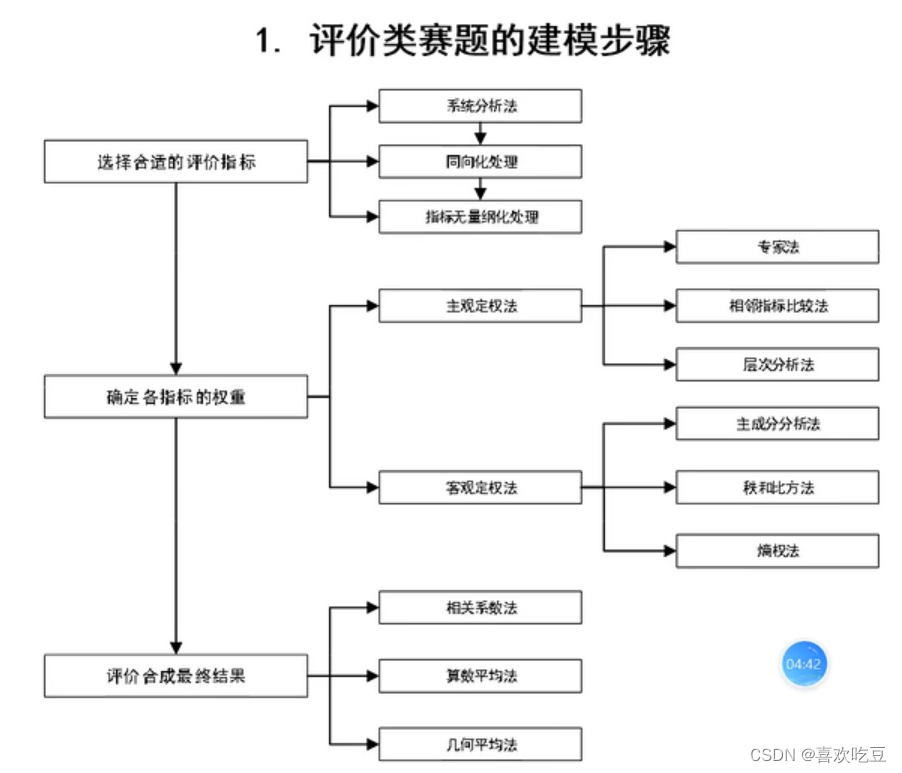
2，主客观评价问题的区别

●主客观概念主要是在指标定权时来划分的。主观评价与客观评价的区别是，主观评价算法在定权时主要以判断者的主观经验为依据，而客观评价则主要基于测量数据的基本特性来综合定权

●定权带有一定的主观性，用不同方法确定的权重分配，可能不尽一致，这将导致权重分配的不确定性，最终可能导致评价结果的不确定性。因而在实际工作中，不论用哪种方法确定权重分配，都应当依赖于较为合理的专业解释。

一般来说，客观定权法更为准确，但是会很麻烦。

3，如何选择合适的评价方法

在评价类问题的分析中，如何选择合适的评价方法是决定评价结果好坏的关键因素，因此需要洞
悉各常用评价方法的基本特性和使用条件才能顺利答题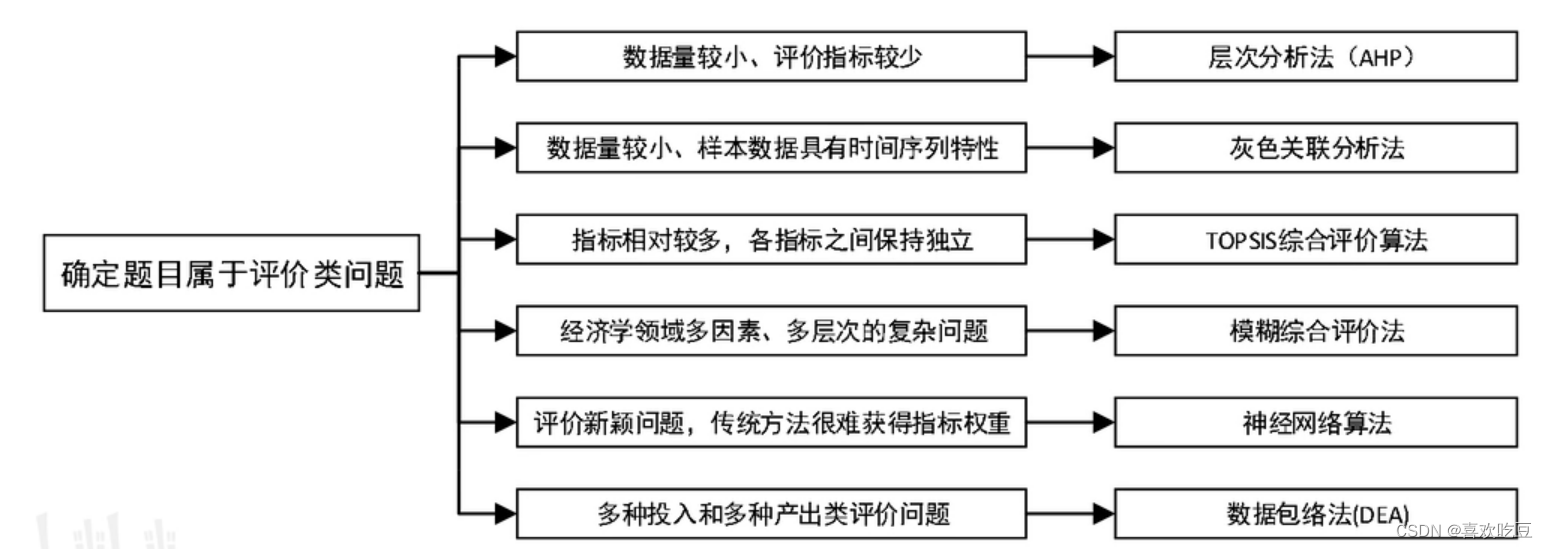

 二，预测类赛题

1，预测类赛题的基本解题步骤

●预测就是根据过去和现在去估计未来，预测未来。统计预测属于预测方法研究范畴，即如何利用科学的统计方法对事物的未来发展进行定量推测

●基于数学建模的预测方法种类繁多，从经典的单耗法、弹性系数法、统计分析法，到目前的灰色预测法。当在使用相应的预测方法建立预测模型时，我们需要知道主要的一些预测方法的研究特点，优缺点和适用范围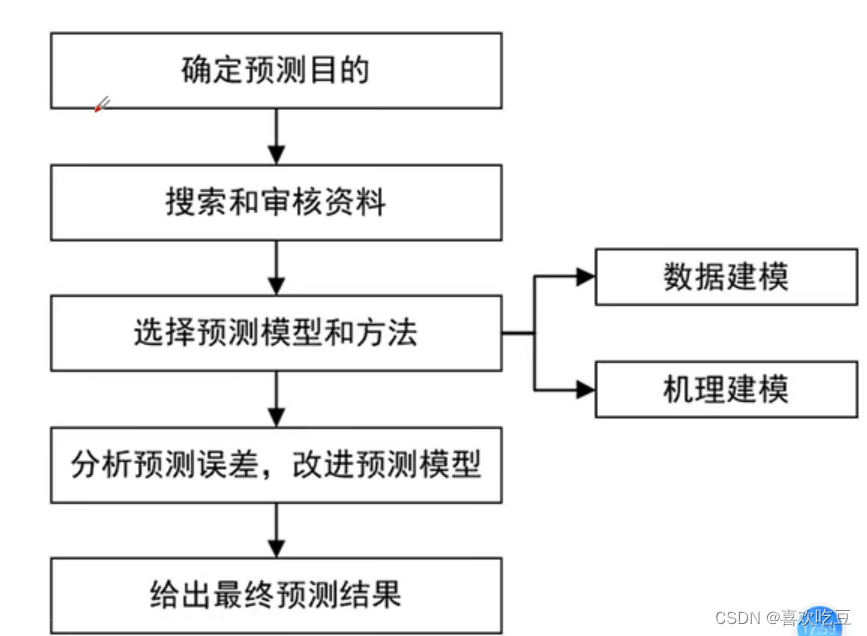

2，预测类问题的区别

●预测类问题分为两类:

●一类是无法用数学语言刻画其内部演化机理的问题;
●另一类是可以通过微分方程刻画其内部规律，这类问题我们称为机理建模问题，通过微分方程建模求解。

3，如何选择合适的预测方法

●在预测类问题的分析中，同样受到预测条件的限制(如数据量的大小、变量之间的关系等)不同的预测方法可能会产生不同的结果，因此需要根据实际情况来选择。
 

 

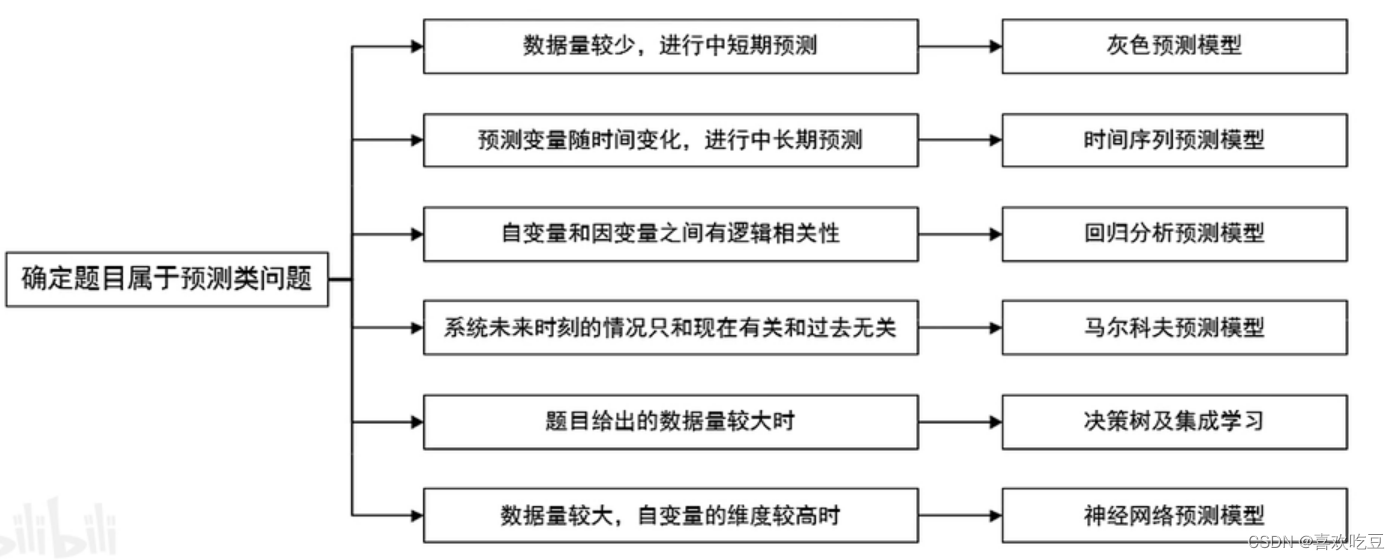
三，优化类赛题

1，优化类赛题的基本解题步骤

●优化类问题是从所有可能方案中选择最合理的方案以达到最优目标。在各种科学问题、工程问题、生产管理、社会经济问题中，人们总是希望在有限的资源条件下，用尽可能小的代价，获得最大的收获(比如保险)。

●优化类问题一般的解题步骤为:

●(1)首先确定决策变量，也就是需要优化的变量;
●(2)然后确定目标函数，也就是优化的目的;
●(3)最后确定约束条件，决策变量在达到最优状态时，受到那些客观限制.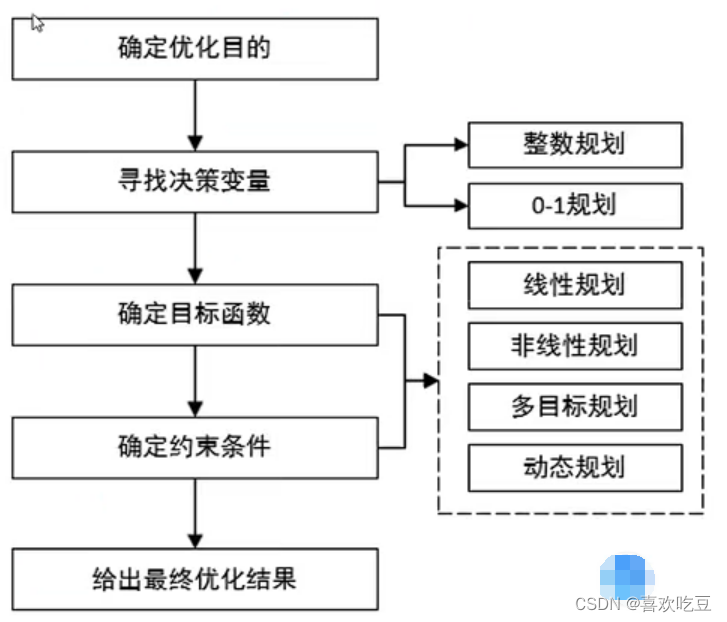

 2，如何选择合适的优化方法

优化类问题中常用的数学模型和求解算法，其中包括线性规划、非线性规划、整数规划、多目标
规划等。在模型求解中，对于凸优化模型，可以采用基于梯度的求解算法;对于非凸的优化模型，
可以采用智能优化算法。