- 1超详细Vue-coderwhy个人学习笔记(一)(Day1-Day2)
- 2MyBatis-@select注解实现模糊查询的两种方式_@select 模糊查询
- 3elmentui中table里面的input无法默认光标_elementui 表单input 光标样式
- 4嵌入式开发实战系列:QSPI Flash驱动功能解析_flash qspi 4
- 5数据结构之——拓补排序和并查集_拓扑排序和并查集区别
- 6element ui多选下拉组件(el-select)tag数量过多处理解决办法(二次封装)_element下拉框数据过多
- 7Elasticsearch和MySQL之间的数据同步问题_elasticsearch同步mysql
- 8微信小程序和vue的区别_微信小程序 vue
- 9修改elementUI 表格透明度,字体颜色_element puls修改表格颜色
- 10利用 Gitlab 搭建 Maven仓库_gitlab搭建maven仓库
LRU算法(详细,java代码实现)_lru java
赞
踩
LRU算法作为面试常问题,是时候深入学习了
1. LRU
1.1. 原理
LRU(Least recently used,最近最少使用)算法根据数据的历史访问记录来进行淘汰数据,其核心思想是“如果数据最近被访问过,那么将来被访问的几率也更高”。
1.2. 实现
最常见的实现是使用一个链表保存缓存数据,详细算法实现如下:

-
新数据插入到链表头部;
-
每当缓存命中(即缓存数据被访问),则将数据移到链表头部;
-
当链表满的时候,将链表尾部的数据丢弃。
1.3. 分析
【命中率】
当存在热点数据时,LRU的效率很好,但偶发性的、周期性的批量操作会导致LRU命中率急剧下降,缓存污染情况比较严重。
【复杂度】
实现简单。
【代价】
命中时需要遍历链表,找到命中的数据块索引,然后需要将数据移到头部。
2. LRU-K
2.1. 原理
LRU-K中的K代表最近使用的次数,因此LRU可以认为是LRU-1。LRU-K的主要目的是为了解决LRU算法“缓存污染”的问题,其核心思想是将“最近使用过1次”的判断标准扩展为“最近使用过K次”。
2.2. 实现
相比LRU,LRU-K需要多维护一个队列,用于记录所有缓存数据被访问的历史。只有当数据的访问次数达到K次的时候,才将数据放入缓存。当需要淘汰数据时,LRU-K会淘汰第K次访问时间距当前时间最大的数据。详细实现如下:
-
数据第一次被访问,加入到访问历史列表;
-
如果数据在访问历史列表里后没有达到K次访问,则按照一定规则(FIFO,LRU)淘汰;
-
当访问历史队列中的数据访问次数达到K次后,将数据索引从历史队列删除,将数据移到缓存队列中,并缓存此数据,缓存队列重新按照时间排序;
-
缓存数据队列中被再次访问后,重新排序;
-
需要淘汰数据时,淘汰缓存队列中排在末尾的数据,即:淘汰“倒数第K次访问离现在最久”的数据。
LRU-K具有LRU的优点,同时能够避免LRU的缺点,实际应用中LRU-2是综合各种因素后最优的选择,LRU-3或者更大的K值命中率会高,但适应性差,需要大量的数据访问才能将历史访问记录清除掉。
2.3. 分析
【命中率】
LRU-K降低了“缓存污染”带来的问题,命中率比LRU要高。
【复杂度】
LRU-K队列是一个优先级队列,算法复杂度和代价比较高。
【代价】
由于LRU-K还需要记录那些被访问过、但还没有放入缓存的对象,因此内存消耗会比LRU要多;当数据量很大的时候,内存消耗会比较可观。
LRU-K需要基于时间进行排序(可以需要淘汰时再排序,也可以即时排序),CPU消耗比LRU要高。
3. Two queues(2Q)
3.1. 原理
Two queues(以下使用2Q代替)算法类似于LRU-2,不同点在于2Q将LRU-2算法中的访问历史队列(注意这不是缓存数据的)改为一个FIFO缓存队列,即:2Q算法有两个缓存队列,一个是FIFO队列,一个是LRU队列。
3.2. 实现
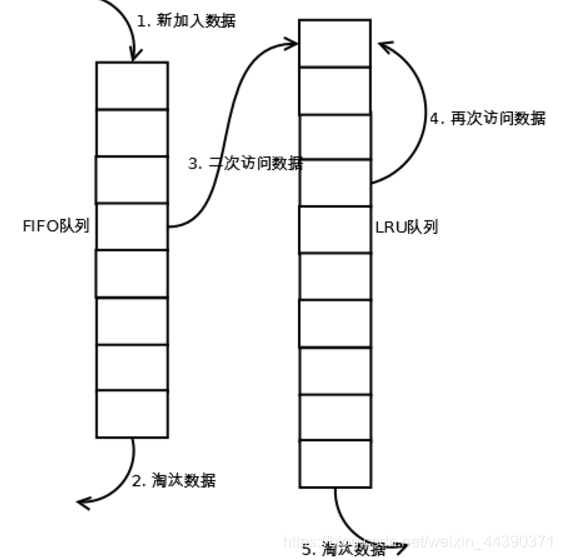
当数据第一次访问时,2Q算法将数据缓存在FIFO队列里面,当数据第二次被访问时,则将数据从FIFO队列移到LRU队列里面,两个队列各自按照自己的方法淘汰数据。详细实现如下:
-
新访问的数据插入到FIFO队列;
-
如果数据在FIFO队列中一直没有被再次访问,则最终按照FIFO规则淘汰;
-
如果数据在FIFO队列中被再次访问,则将数据移到LRU队列头部;
-
如果数据在LRU队列再次被访问,则将数据移到LRU队列头部;
-
LRU队列淘汰末尾的数据。
注:上图中FIFO队列比LRU队列短,但并不代表这是算法要求,实际应用中两者比例没有硬性规定。
3.3. 分析
【命中率】
2Q算法的命中率要高于LRU。
【复杂度】
需要两个队列,但两个队列本身都比较简单。
【代价】
FIFO和LRU的代价之和。
2Q算法和LRU-2算法命中率类似,内存消耗也比较接近,但对于最后缓存的数据来说,2Q会减少一次从原始存储读取数据或者计算数据的操作。
4. Multi Queue(MQ)
4.1. 原理
MQ算法根据访问频率将数据划分为多个队列,不同的队列具有不同的访问优先级,其核心思想是:优先缓存访问次数多的数据。
4.2. 实现
MQ算法将缓存划分为多个LRU队列,每个队列对应不同的访问优先级。访问优先级是根据访问次数计算出来的,例如
详细的算法结构图如下,Q0,Q1…Qk代表不同的优先级队列,Q-history代表从缓存中淘汰数据,但记录了数据的索引和引用次数的队列:

如上图,算法详细描述如下:
-
新插入的数据放入Q0;
-
每个队列按照LRU管理数据;
-
当数据的访问次数达到一定次数,需要提升优先级时,将数据从当前队列删除,加入到高一级队列的头部;
-
为了防止高优先级数据永远不被淘汰,当数据在指定的时间里访问没有被访问时,需要降低优先级,将数据从当前队列删除,加入到低一级的队列头部;
-
需要淘汰数据时,从最低一级队列开始按照LRU淘汰;每个队列淘汰数据时,将数据从缓存中删除,将数据索引加入Q-history头部;
-
如果数据在Q-history中被重新访问,则重新计算其优先级,移到目标队列的头部;
-
Q-history按照LRU淘汰数据的索引。
4.3. 分析
【命中率】
MQ降低了“缓存污染”带来的问题,命中率比LRU要高。
【复杂度】
MQ需要维护多个队列,且需要维护每个数据的访问时间,复杂度比LRU高。
【代价】
MQ需要记录每个数据的访问时间,需要定时扫描所有队列,代价比LRU要高。
注:虽然MQ的队列看起来数量比较多,但由于所有队列之和受限于缓存容量的大小,因此这里多个队列长度之和和一个LRU队列是一样的,因此队列扫描性能也相近。
5. LRU类算法对比
由于不同的访问模型导致命中率变化较大,此处对比仅基于理论定性分析,不做定量分析。
| 对比点 | 对比 |
|---|---|
| 命中率 | LRU-2 > MQ(2) > 2Q > LRU |
| 复杂度 | LRU-2 > MQ(2) > 2Q > LRU |
| 代价 | LRU-2 > MQ(2) > 2Q > LRU |
实际应用中需要根据业务的需求和对数据的访问情况进行选择,并不是命中率越高越好。例如:虽然LRU看起来命中率会低一些,且存在”缓存污染“的问题,但由于其简单和代价小,实际应用中反而应用更多。
java中最简单的LRU算法实现,就是利用jdk的LinkedHashMap,覆写其中的removeEldestEntry(Map.Entry)方法即可
如果你去看LinkedHashMap的源码可知,LRU算法是通过双向链表来实现,当某个位置被命中,通过调整链表的指向将该位置调整到头位置,新加入的内容直接放在链表头,如此一来,最近被命中的内容就向链表头移动,需要替换时,链表最后的位置就是最近最少使用的位置。
import java.util.ArrayList; import java.util.Collection; import java.util.LinkedHashMap; import java.util.concurrent.locks.Lock; import java.util.concurrent.locks.ReentrantLock; import java.util.Map; /** * 类说明:利用LinkedHashMap实现简单的缓存, 必须实现removeEldestEntry方法,具体参见JDK文档 * * @author dennis * * @param <K> * @param <V> */ public class LRULinkedHashMap<K, V> extends LinkedHashMap<K, V> { private final int maxCapacity; private static final float DEFAULT_LOAD_FACTOR = 0.75f; private final Lock lock = new ReentrantLock(); public LRULinkedHashMap(int maxCapacity) { super(maxCapacity, DEFAULT_LOAD_FACTOR, true); this.maxCapacity = maxCapacity; } @Override protected boolean removeEldestEntry(java.util.Map.Entry<K, V> eldest) { return size() > maxCapacity; } @Override public boolean containsKey(Object key) { try { lock.lock(); return super.containsKey(key); } finally { lock.unlock(); } } @Override public V get(Object key) { try { lock.lock(); return super.get(key); } finally { lock.unlock(); } } @Override public V put(K key, V value) { try { lock.lock(); return super.put(key, value); } finally { lock.unlock(); } } public int size() { try { lock.lock(); return super.size(); } finally { lock.unlock(); } } public void clear() { try { lock.lock(); super.clear(); } finally { lock.unlock(); } } public Collection<Map.Entry<K, V>> getAll() { try { lock.lock(); return new ArrayList<Map.Entry<K, V>>(super.entrySet()); } finally { lock.unlock(); } } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
基于双链表 的LRU实现:
传统意义的LRU算法是为每一个Cache对象设置一个计数器,每次Cache命中则给计数器+1,而Cache用完,需要淘汰旧内容,放置新内容时,就查看所有的计数器,并将最少使用的内容替换掉。
它的弊端很明显,如果Cache的数量少,问题不会很大, 但是如果Cache的空间过大,达到10W或者100W以上,一旦需要淘汰,则需要遍历所有计算器,其性能与资源消耗是巨大的。效率也就非常的慢了。
它的原理: 将Cache的所有位置都用双连表连接起来,当一个位置被命中之后,就将通过调整链表的指向,将该位置调整到链表头的位置,新加入的Cache直接加到链表头中。
这样,在多次进行Cache操作后,最近被命中的,就会被向链表头方向移动,而没有命中的,而想链表后面移动,链表尾则表示最近最少使用的Cache。
当需要替换内容时候,链表的最后位置就是最少被命中的位置,我们只需要淘汰链表最后的部分即可。
- 1
- 2
- 3
- 4
- 5
上面说了这么多的理论, 下面用代码来实现一个LRU策略的缓存。
我们用一个对象来表示Cache,并实现双链表
- 1
public class LRUCache { /** * 链表节点 * @author Administrator * */ class CacheNode { …… } private int cacheSize;//缓存大小 private Hashtable nodes;//缓存容器 private int currentSize;//当前缓存对象数量 private CacheNode first;//(实现双链表)链表头 private CacheNode last;//(实现双链表)链表尾 }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
下面给出完整的实现,这个类也被Tomcat所使用( org.apache.tomcat.util.collections.LRUCache),但是在tomcat6.x版本中,已经被弃用,使用另外其他的缓存类来替代它。
public class LRUCache { /** * 链表节点 * @author Administrator * */ class CacheNode { CacheNode prev;//前一节点 CacheNode next;//后一节点 Object value;//值 Object key;//键 CacheNode() { } } public LRUCache(int i) { currentSize = 0; cacheSize = i; nodes = new Hashtable(i);//缓存容器 } /** * 获取缓存中对象 * @param key * @return */ public Object get(Object key) { CacheNode node = (CacheNode) nodes.get(key); if (node != null) { moveToHead(node); return node.value; } else { return null; } } /** * 添加缓存 * @param key * @param value */ public void put(Object key, Object value) { CacheNode node = (CacheNode) nodes.get(key); if (node == null) { //缓存容器是否已经超过大小. if (currentSize >= cacheSize) { if (last != null)//将最少使用的删除 nodes.remove(last.key); removeLast(); } else { currentSize++; } node = new CacheNode(); } node.value = value; node.key = key; //将最新使用的节点放到链表头,表示最新使用的. moveToHead(node); nodes.put(key, node); } /** * 将缓存删除 * @param key * @return */ public Object remove(Object key) { CacheNode node = (CacheNode) nodes.get(key); if (node != null) { if (node.prev != null) { node.prev.next = node.next; } if (node.next != null) { node.next.prev = node.prev; } if (last == node) last = node.prev; if (first == node) first = node.next; } return node; } public void clear() { first = null; last = null; } /** * 删除链表尾部节点 * 表示 删除最少使用的缓存对象 */ private void removeLast() { //链表尾不为空,则将链表尾指向null. 删除连表尾(删除最少使用的缓存对象) if (last != null) { if (last.prev != null) last.prev.next = null; else first = null; last = last.prev; } } /** * 移动到链表头,表示这个节点是最新使用过的 * @param node */ private void moveToHead(CacheNode node) { if (node == first) return; if (node.prev != null) node.prev.next = node.next; if (node.next != null) node.next.prev = node.prev; if (last == node) last = node.prev; if (first != null) { node.next = first; first.prev = node; } first = node; node.prev = null; if (last == null) last = first; } private int cacheSize; private Hashtable nodes;//缓存容器 private int currentSize; private CacheNode first;//链表头 private CacheNode last;//链表尾 }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
转载自: https://www.iteye.com/blog/flychao88-1977653



