现代信号处理——经典谱估计_信号谱估计

一、BT法（间接法）

BT法是先估计自相关函数，然后进行傅里叶变换得到功率谱。

有偏自相关函数估计的误差相对较小，是一种渐近一致估计（渐近无偏估计）：

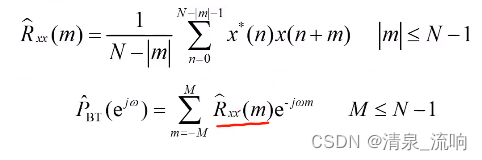
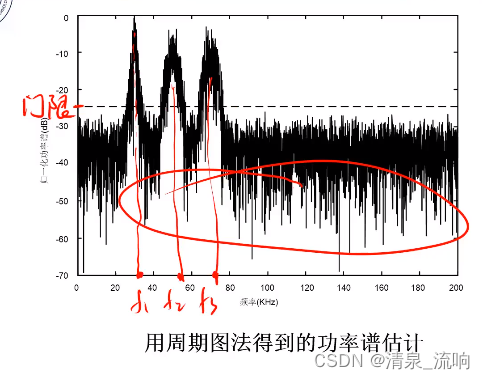
二、周期图法（直接法） 

整个计算过程中没有计算样本的自相关，拿到随机信号的样本后，直接对样本进行傅里叶变换，跳过了样本自相关计算的过程。

周期图法的定义如下：

1、周期图与BT法的等价关系

 令m=k-n，即k=m+n,则

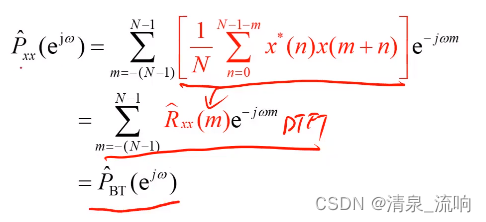
 2、周期图法谱估计质量分析

周期图是有偏估计，当N→oo时，周期图的统计平均值趋于它的真值，因此周期图属于渐近无偏估计。

周期图估计的功率谱起伏很大，是一种很差的功率谱估计方法。

 

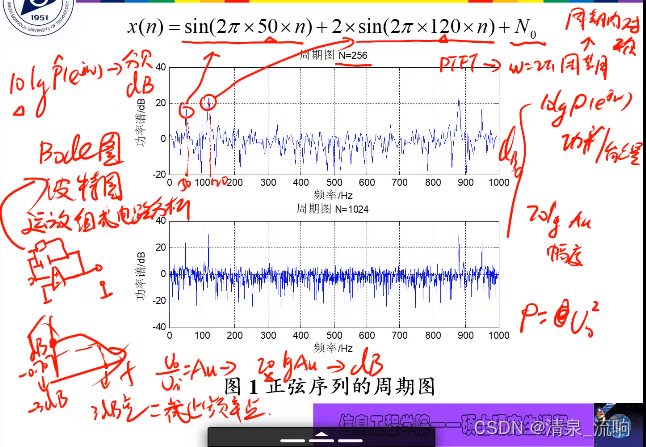
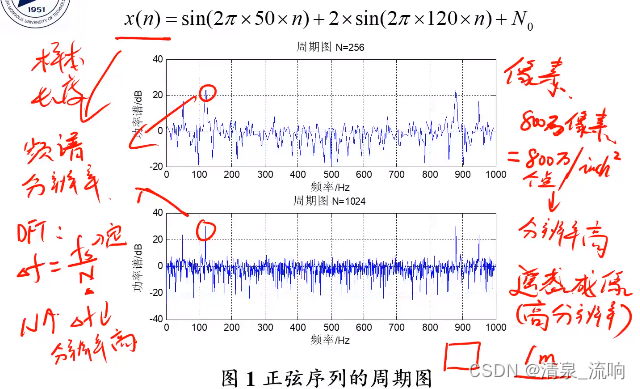
三、经典谱估计方法改进 

存在问题：BT法和周期图法估计功率谱都不是一致估计，频率分辨率低。

解决方法：对周期图进行修正，使其满足一致估计条件。可以采用平滑处理的方法，使其方差减小。

Bartlett平均周期图法

窗口处理法平均周期图

Welch法（修正的周期图求平均法）

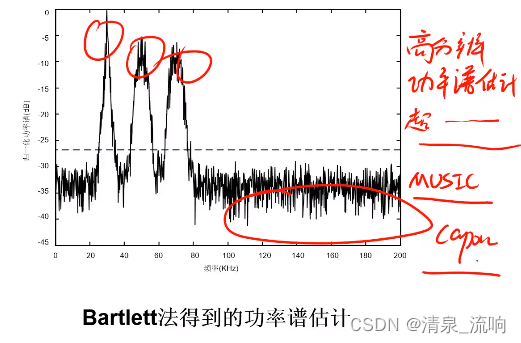
1、Bartlett平均周期图法（功率谱加三角窗）

主要思想：对序列x(n)进行L次独立观测或将其分成L段，计算每组观测数据的周期图，再将L个周期图加和后求平均。

估计方法：假设随机信号x(n)的观测数据区间为：0≤n≤M-1，共进行了L次独立观测，得到L组记录数据，每一组记录数据用xi(n)，i=1,2,3,…,L表示；

或对长为N的数据x(n)分成L段，每段有M个数据，N=LM，第i段数据表示为xi(n)=x(n+iM-M)。

第i组的周期图用下式表示： 

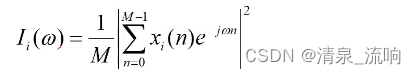
 将得到的L个周期图进行平均，作为信号x(n)的功率谱估计，公式如下：

 

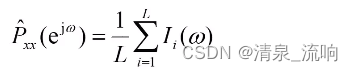
估计效果分析

偏移分析：

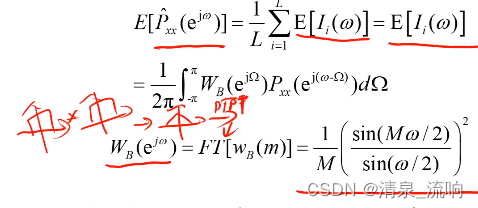
平均周期图仍然是有偏估计，偏移和每一段的数据个数M有关；

偏移的大小反映分辨率的高低。

方差分析：

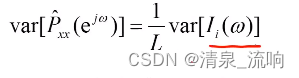
平均周期图的估计方差是周期图的方差的1/L，L越大方差越小，功率谱越平滑；相应的，M越小，偏移越大，分辨率越低；

估计的均方误差也减少；

以分辨率的降低换取了估计方差的减少，估计量的方差和分辨率是一对矛盾。 

 

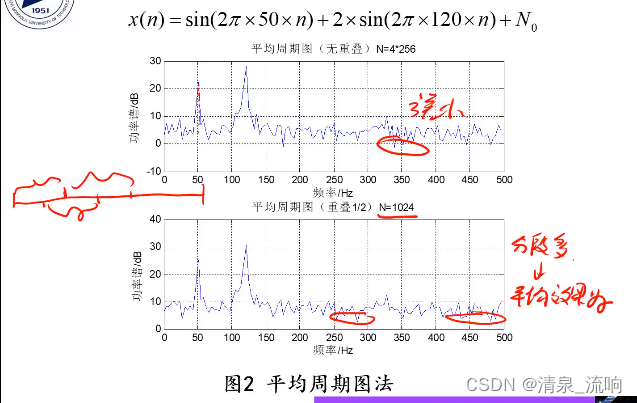
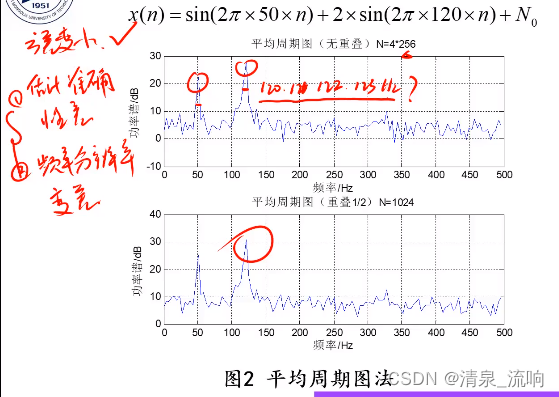
2、窗口处理法平均周期图

主要思想：用一适当的功率谱窗函数W(e^jw)与周期图进行卷积，来达到使周期图平滑的目的。

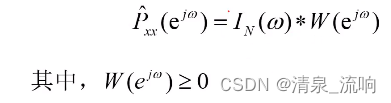
估计效果分析： 

偏移分析：

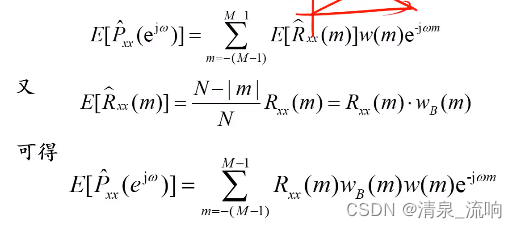
周期图的窗函数法仍然是有偏估计，其偏移和wB(m)、w(m)两个窗函数有关。 

 

 

 

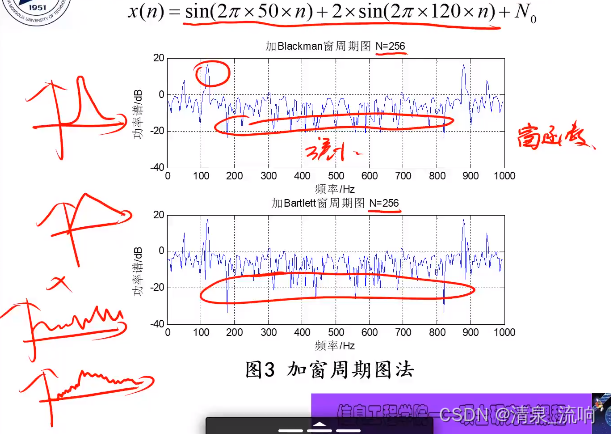
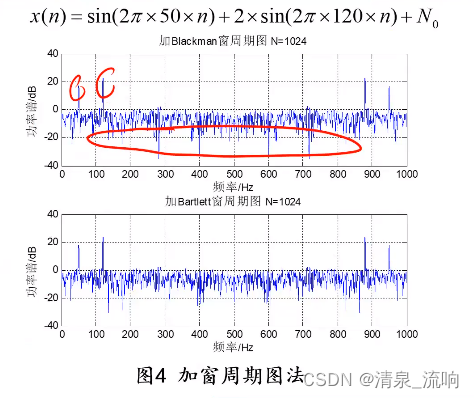
 3、修正的周期图求平均法（Welch法：分段+窗函数）

主要思想：对Bartlett法进行修正，使之更适合FFT计算。

选择适当的窗函数w(n)，并在周期图计算前直接加进去；

在分段时，可使各段之间有重迭，这样将会使方差减小。

估计方法：首先把数据长度为N的信号x(n)分成L段，每一段数据长度为M；

然后把窗函数w(n)加到每一个数据段上，求出每一段的周期图，形成修正的周期图；

再对每一个修正的周期图进行平均。

 

 

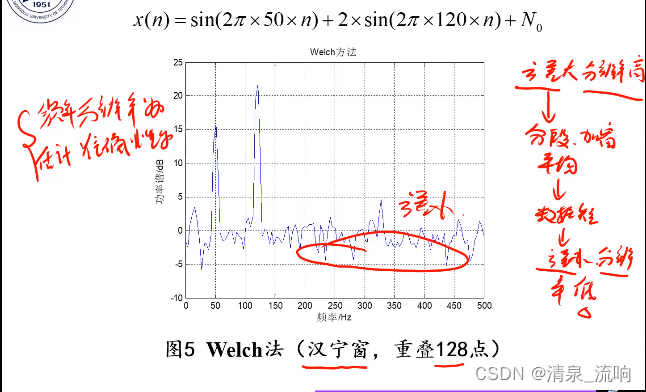
结论：传统的功率谱估计方法无论采取哪一种改进方法，总是以减少分辨率为代价，换取估计方差的减少，提高分辨率的问题无法根本解决。

 

 

 

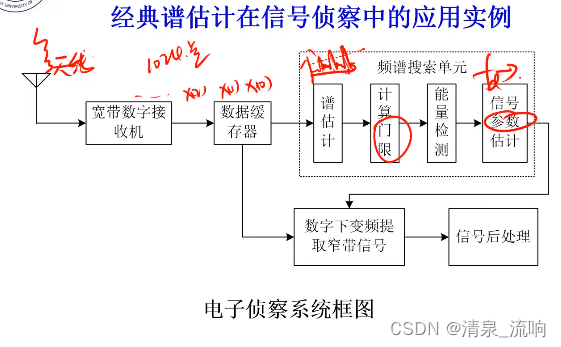
参考视频：

https://www.bilibili.com/video/BV1wS4y1D7ng?p=5&vd_source=77c874a500ef21df351103560dada737