文本分类的14种算法（2）

文本分类的14种算法（2）：

部分常用文本分类算法

决策树

决策树从根结点开始，根据待分类数据的某一特征的取值对其进行划分，分配到相应子结点。像这样递归进行，直到到达叶结点。那么如何判定最优特征呢？
先放几个定义：
1.随机变量X的熵定义为：
H( p )=-∑pi*log(pi)
熵越大，随机变量的不确定性越大
2.H(Y|X)称为随机变量X给定的条件下随机变量Y的条件熵
H(Y|X)=∑p(X=xi)*H(Y|X=xi)=∑p(X=xi)*∑(p(Y=yj|X=xi)*log(p(Y=yj|X=xi)))
这张图挺好的，可以搭配着理解一下，注意C是根据类别划分的，D是根据特征划分的：

于是上式中的X=xi即特征值变量A取某特征值，Y=yj即分类为yj。
信息增益表示得知特征X的信息而使得类Y的信息的不确定性减少程度，即：
g(D|A)=H(D)-H(D|A)
决策树就是计算其每个特征的信息增益，比较它们的大小，递归选择信息增益最大的特征，即：
1）构建根节点，将所有训练数据都放在根节点，选择一个最优特征，按着这一特征将训练数据集分割成子集，使得各个子集有一个在当前条件下最好的分类。
2） 如果这些子集已经能够被基本正确分类，那么构建叶节点，并将这些子集分到所对应的叶节点去。
3）如果还有子集不能够被正确的分类，那么就对这些子集选择新的最优特征，继续对其进行分割，构建相应的节点，如果递归进行，直至所有训练数据子集被基本正确的分类，或者没有合适的特征为止。
4）每个子集都被分到叶节点上，即都有了明确的类，这样就生成了一颗决策树。

可见，决策树有一个显著的缺陷，就是训练集所能的逻辑范围必须覆盖测试集的逻辑范围。比如说我选取特征性别分类，性别有两种取值男和女，结果测试集里有一个人妖，就完蛋了。
常见的决策树生成算法有ID3,C4.5和CART：
1)ID3，采用熵（entropy）来度量信息不确定度，选择“信息增益”最大的作为节点特征，它是多叉树，即一个节点可以有多个分支。结束条件一般是信息增益小于某阈值。
2)C4.5，同样采用熵（entropy）来度量信息不确定度，选择“信息增益比”最大的作为节点特征，同样是多叉树，即一个节点可以有多个分支。结束条件一般是信息增益比小于某阈值。
3)CART，采用基尼指数（Gini index）来度量信息不确定度，选择基尼指数最小的作为节点特征，它是二叉树，即一个节点只分两支。结束条件一般是结点样本个数小于阈值。
python的sklearn包默认使用的是利用基尼指数衡量不确定度的CART分类器，但可以改成entropy：

可见，CART就是将分类标准由某特征取什么值细化为某特征值取不取某个值。
用上次的例子和代码跑一下：

dtc = DecisionTreeClassifier()
classificate(dtc, trainCount, trainLable, testCount, testLable)
1
2

朴素贝叶斯（高斯、多项式、伯努利）

朴素贝叶斯的公式，前面我的文章说过python对其的处理和优化：
https://blog.csdn.net/qq_43012160/article/details/94664377

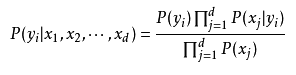
sklearn包提供了朴素贝叶斯有三种常用模型：
高斯贝叶斯GaussianNB、多项式贝叶斯MultinomialNB和伯努利贝叶斯BernoulliNB。
分别对应数据满足高斯分布（正态分布）、多项式分布和伯努利分布的训练集数据。
其中高斯贝叶斯常被用来处理连续数据（如身高），文本分类中常用的是进行离散数据处理的伯努利贝叶斯和多项式贝叶斯。

1)伯努利贝叶斯：

伯努利贝叶斯即特征的取值只有取和不取两类（0和1），在朴素贝叶斯公式种，
p(yi)=标签为yi的文本数（句子数）/文本总数（句子总数）
p(xj|yi)=(标签为yi的文本中出现了单词xj的文本数+1)/(标签为yi的文本数+2)。
例如：

P(Chinese|yes)=（3+1）/（3+2）=4/5.
伯努利贝叶斯主要用在样本特征是二元离散值或者很稀疏的多元离散值的时候。

2)多项式贝叶斯：

多项式贝叶斯其实就是伯努利贝叶斯的特征取值由简单的0-1扩展为多个值的情况。
p(yi)=标签为yi的文本中的单词总数/训练集中的单词总数
p(xj|yi)=(标签为yi的文本中单词xj的出现次数+1)/(标签为yi的文本中的单词总数+词袋单词种数)。
还是上面那个例子：
P(Chinese|yes)=（5+1）/（8+6）=6/14=3/7.
多项式贝叶斯主要用在样本特征大部分是是多元离散值的时候。

上面放的那篇文章好像写了一个四不像，p(yi)用的伯努利贝叶斯，p(xj|yi)用的多项式贝叶斯。。。
下面是多项式贝叶斯、伯努利贝叶斯和高斯贝叶斯跑出来的结果；
由于训练集是离散数据，高斯贝叶斯的性能明显差了一些：
多项式贝叶斯：

伯努利贝叶斯：

高斯贝叶斯：