热门标签
当前位置: article > 正文
绘图杂记【1】Python、R等绘图_moo..koko.oom.kp.(okkoo.(.o.ooo.ooo.oo(koonp.?nkok
作者:凡人多烦事01 | 2024-03-16 18:07:57
赞
踩
moo..koko.oom.kp.(okkoo.(.o.ooo.ooo.oo(koonp.?nkok.ppmoook..pkokoonop.kp
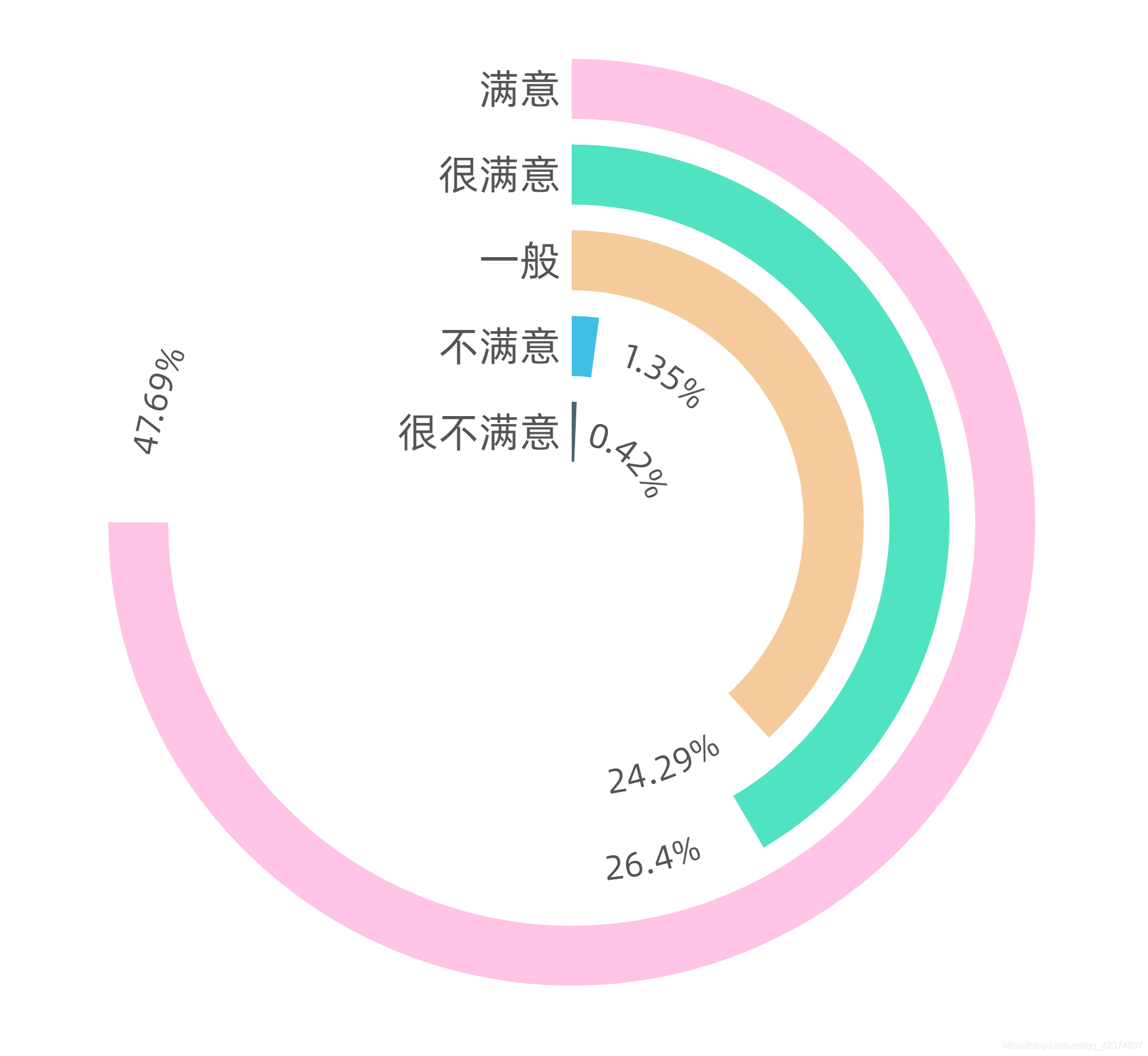
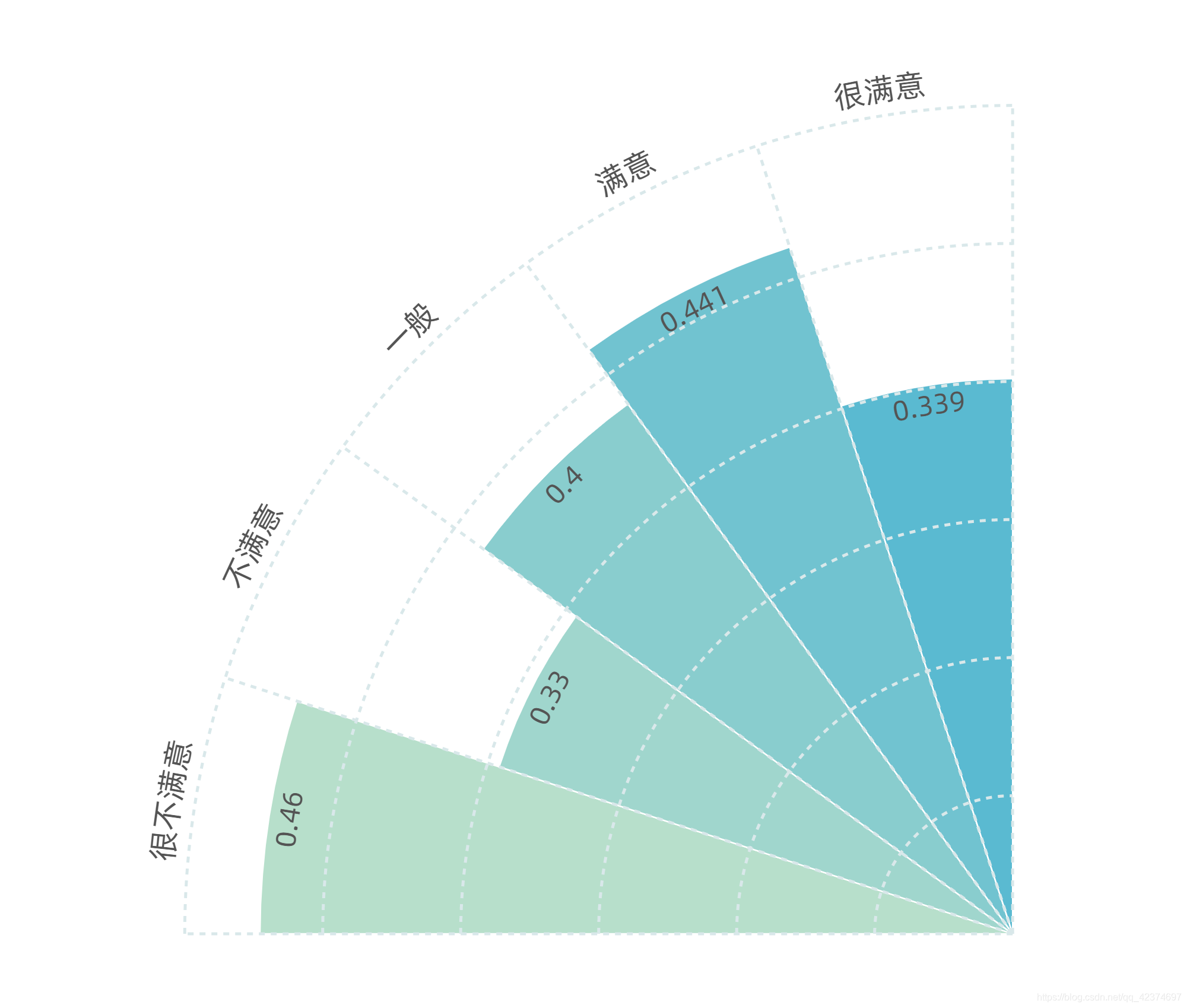
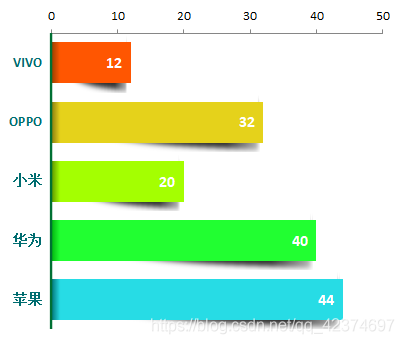
pyhton代码和echarts代码
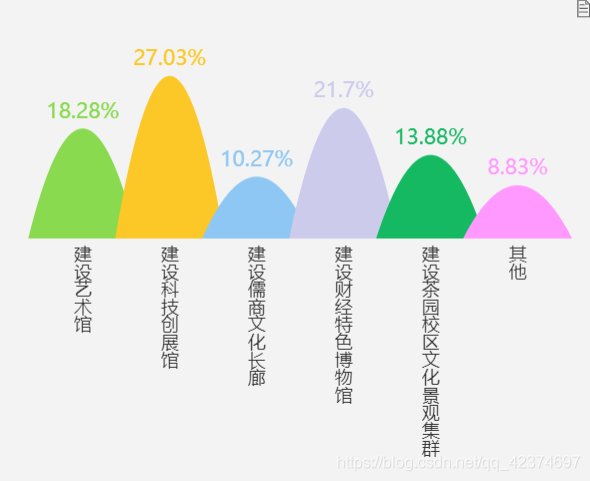
option = { toolbox: { show: true, feature: { dataView: {show:true}, saveAsImage: { //excludeComponents :['toolbox'], pixelRatio: 20 } } }, tooltip: { legend: {}, trigger: 'axis', axisPointer: { type: 'none' }, formatter: function (params) { return params[0].name + ': ' + params[0].value; } }, xAxis: { data: ['建设艺术馆', '建设科技创展馆', '建设儒商文化长廊', '建设财经特色博物馆', '建设茶园校区文化景观集群' ,'其他'], axisTick: {show: false}, axisLine: {show: false}, axisLabel: { textStyle: { color: '#00000', }, //rotate:90, interval: 0, formatter:function(value) { return value.split("").join("\n"); }, textStyle: { fontSize : 16 //更改坐标轴文字大小 } } }, yAxis: { splitLine: {show: false}, axisTick: {show: false}, axisLine: {show: false}, axisLabel: {show: false} }, grid: [ {bottom: '50%'}, {top: '10%'} ], color: ['#89DA4F','#FCC828','#8EC7F4','#CDCBEC','#14B961'], series: [{ name: 'hill', barWidth :99, type: 'pictorialBar', barCategoryGap: '0%', // symbol: 'path://M0,10 L10,10 L5,0 L0,10 z', symbol: 'path://path://M10 600 Q 95 0 180 600', label:{ normal:{ show: true, position: 'top', formatter:'{c}%', fontSize:19 } }, itemStyle: { normal: { opacity: 1, color: function (params){ var colorList = ['#89DA4F','#FCC828','#8EC7F4','#CDCBEC','#14B961','#FF99FF']; return colorList[params.dataIndex]; } }, emphasis: { opacity: 1 } }, data: [18.28, 27.03, 10.27, 21.70, 13.88,8.83], }] };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
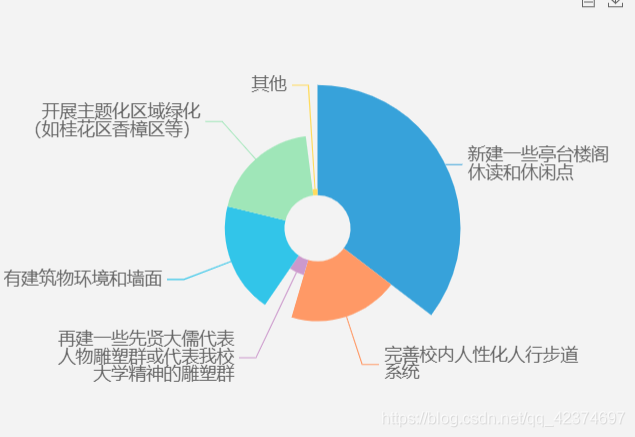
var scale = 1; option = { tooltip : { trigger: 'item', formatter: "{a} <br/>{b} : {c} ({d}%)" }, title: { text:'学生', left:'center', top:'47%', // padding:[24,0], textStyle:{ color:'#031f2d', fontSize:20*scale, align:'center' } }, series: [ { name: '半径模式', type: 'pie', radius: [50, 130], center: ['50%', '50%'], roseType: 'radius', labelLine:{ normal:{ length:0.1, // 改变标示线的长度 lineStyle: { } }, }, avoidLabelOverlap: false, hoverAnimation: true, label: { emphasis: {//中间文字显示 show: false, } }, emphasis: { label: { show: true, } }, data: [ {value: 35, name: '新建一些亭台楼阁\n休读和休闲点', }, {value: 19, name: '完善校内人性化人行步道\n系统', itemStyle: { color: '#FF9966', }, }, {value: 5, name: '再建一些先贤大儒代表\n人物雕塑群或代表我校\n大学精神的雕塑群', itemStyle: { color: '#CC99CC', }, }, {value: 19, name: '美化现有建筑物环境和墙面'}, {value: 19, name: '开展主题化区域绿化\n(如桂花区香樟区等)'}, {value: 2, name: '其他'}, ] }, ] };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79

option = { toolbox: { show: true, feature: { dataView: {show:true}, saveAsImage: { //excludeComponents :['toolbox'], pixelRatio: 20 } } }, series: [ { name: '半径模式', type: 'pie', radius: [50, 110], center: ['49%', '29%'], roseType: 'radius', labelLine:{ normal:{ length:0.1, // 改变标示线的长度 lineStyle: { } }, }, avoidLabelOverlap: false, label: { normal: { show: true, position: 'center', color:'#4c4a4a', formatter: '{total|'+'学生}', rich: { total:{ fontSize: 18, fontFamily : "微软雅黑", color:'#454c5c' }, active: { fontFamily : "微软雅黑", fontSize: 17, color:'#6c7a89', lineHeight:30, }, } }, emphasis: {//中间文字显示 show: true, } }, data: [ {value: 36.56, name: '新建一些亭台楼阁\n休读和休闲点', }, {value: 18.51, name: '完善校内人性化人行步道\n系统', itemStyle: { color: '#FF9966', }, }, {value: 4.65, name: '再建一些先贤大儒代表\n人物雕塑群或代表我校\n大学精神的雕塑群', itemStyle: { color: '#CC99CC', }, }, {value: 19.53, name: '美化现有建筑物环境和墙面'}, {value: 18.51, name: '开展主题化区域绿化\n(如桂花区香樟区等)'}, {value: 2.25, name: '其他'}, ] }, { name: '半径模式', type: 'pie', radius: [50, 130], center: ['23%', '70%'], roseType: 'radius', labelLine:{ normal:{ length:0.1, // 改变标示线的长度 lineStyle: { } }, }, avoidLabelOverlap: false, label: { normal: { show: true, position: 'center', color:'#4c4a4a', formatter: '{total|'+'教师}', rich: { total:{ fontSize: 18, fontFamily : "微软雅黑", color:'#454c5c' }, active: { fontFamily : "微软雅黑", fontSize: 17, color:'#6c7a89', lineHeight:30, }, } }, emphasis: {//中间文字显示 show: true, } }, data: [ {value: 23.06, name: '新建一些亭台楼阁\n休读和休闲点', }, {value: 28.15, name: '完善校内人性化人行步道\n系统', itemStyle: { color: '#FF9966', }, }, {value: 4.83, name: '再建一些先贤大儒代表\n人物雕塑群或代表我校\n大学精神的雕塑群', itemStyle: { color: '#CC99CC', }, }, {value: 15.01, name: '美化现有建筑物环境和墙面'}, {value: 24.93, name: '开展主题化区域绿化\n(如桂花区香樟区等)'}, {value: 4.02, name: '其他'}, ] }, { name: '半径模式', type: 'pie', radius: [50, 130], center: ['77%', '70%'], roseType: 'radius', labelLine:{ normal:{ length:0.1, // 改变标示线的长度 lineStyle: { } }, }, avoidLabelOverlap: false, label: { normal: { show: true, position: 'center', color:'#4c4a4a', formatter: '{total|'+'校友}', rich: { total:{ fontSize: 18, fontFamily : "微软雅黑", color:'#454c5c' }, active: { fontFamily : "微软雅黑", fontSize: 17, color:'#6c7a89', lineHeight:30, }, } }, emphasis: {//中间文字显示 show: true, } }, data: [ {value: 22.64, name: '新建一些亭台楼阁\n休读和休闲点', }, {value: 16.98, name: '完善校内人性化人行步道\n系统', itemStyle: { color: '#FF9966', }, }, {value: 11.32, name: '再建一些先贤大儒代表\n人物雕塑群或代表我校\n大学精神的雕塑群', itemStyle: { color: '#CC99CC', }, }, {value: 24.53, name: '美化现有建筑物环境和墙面'}, {value: 20.75, name: '开展主题化区域绿化\n(如桂花区香樟区等)'}, {value: 3.77, name: '其他'}, ] }, ] };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- 197
- 198
- 199
- 200
- 201
- 202
- 203
- 204
- 205
- 206
- 207
- 208
- 209
- 210
- 211
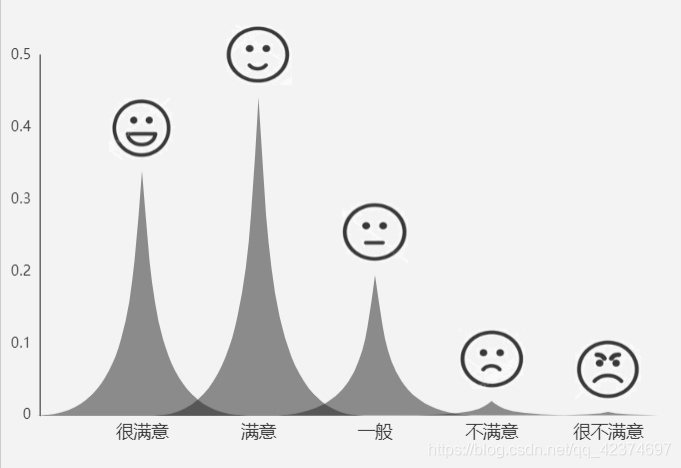
模糊综合评价的图
echarts代码
var pathSymbols = { reindeer: 'image://data:image/jpg;base64,iVBORw0KGgoAAAANSUhEUgAAAKcAAACbCAYAAAAHros6AABIY0lEQVR42u3dVZNz63H28f0dcpAchpmZmZmZmROHyQGHHE4cZmZmZo4TJw4zMzOn9NZPVf9d7dtLGmlGM8/j/e6DVYLRSGvdq++Gq6/ufmC32z1wPx7/+7//u/vv//7vnef/93//t/uf//mfnfc87zO97/DZPtN7Hd7b+g1/m7/Vd/R9//Vf/7X7z//8z916Xh0+M//X+cxzPfR/PtN59tj/zmvsuzvPed1zHY4dfef87du6Z/MaOrbu26nHA/ercHaRV/29BVkvfn2v51OQEypC6JhC4P3/+I//2P3zP//z7l//9V/3j3/7t3+7+8u//MvdX/3VX+3++q//ev/8T//0T3d//Md/vPujP/qj3Z/8yZ/sXzv+/M//fP+5v//7v9/94z/+4/47CHq/5bnvT6i3risBXTdb593mmILQtV21Hrd1vw4dDynhvGpBt4Rz67NuFCHY0mQJi787Ek7f428E8h/+4R/2gvh7v/d7u1/4hV/Y/eiP/uju+77v+3bf9V3ftfu2b/u23bd+67fuvvmbv3n3Td/0TftHr7/92799993f/d37z/3cz/3c7vGPf/zud3/3d3d/8Rd/sRfWf/u3f3sibdj5HNLYV1mYrqNrum0tuXUeq7Wa9+c633lfC+c0h130sQvdWgj/m1acbkBCS/houl/91V/d/eRP/uTue77ne3Zf+7Vfu/vcz/3c3ad8yqfsPviDP3j3/u///rv3eI/32L3DO7zD7q3f+q13b/VWb7V7y7d8y92bv/mb797ojd5o9wZv8Aa713/9198fb/iGb7h74zd+4/3ffObt3u7tdu/2bu+2+4AP+IDdox71qN0nfuIn7j7ncz5n91Vf9VW7b/mWb9kL++Me97jdb/7mb+61bZrUOR8TgOkOTNdiujdXbdxLKpEtjX7T37zvhbMLd7NWEzhvWNpm9f0IYML57//+77u/+Zu/2ZtfwvDzP//zux/8wR/caz0CQ3je8z3fcy98r/M6r7N75Vd+5d2LvdiL7V70RV9094Iv+IK753u+59s97/M+7/54rud6rt1zPMdz7J792Z99fzzbsz3b7lmf9Vn3j17723M+53PuH33+hV/4hXcv+ZIvuXuFV3iF/XcT8nd913fdffiHf/juUz/1U3df+IVfuNe8P/3TP73fKL//+7+/3zj/8i//sr+u6QdPK3DMp7sL4Zz+89bmeMgK51aQsAptJjkhnJ/JNFqwf/qnf9r9zu/8zu4HfuAHdp//+Z+/14gE5FVe5VV2L/3SL717/ud//r1QEbCOZ37mZ94LpL+9wAu8wF7ACOqLv/iL7x9f5EVeZP+ex553vNALvdBeoHvf8+d5nud58DcIMeH1t5d5mZfZvdIrvdJeaN/+7d9+96Ef+qG7L/qiL9r90A/90O4P/uAP9r5uweG6MW041721Pqes7yWFc2r1S3z3fR8QbV3kat5W7eA9vt0f/uEf7v1E/iHN9DEf8zF7E8v00oov9VIv9aBWJDi0IS1HEL3n8LzXBG4KXwcB9D29nzASat/ncf6/x77Xb/ptn/E9L/ESL7F7uZd7ud3rvu7r7t7mbd5m9yEf8iG7z/iMz9j7sa5F8MUXzqTzXxPOaV6vcoEupTi2AqFL/e4D9zuUtAYyme8JA3nuPSaQlmESf+qnfmrv0z3mMY/Zm+rXfu3X3r3sy77sXkgyuWnFHtN0THnmPA14TFB9zuenJk0A+26v07o+67W/eSSgzme6DDTsszzLs+x/69Ve7dV27/Iu77L7uI/7uL0/zPQLsPioM+LPkhDYuUa3bdFuy32476LyYxdXREoIp69Jk4ioCeWP/diP7T7zMz9z97Zv+7Z7DUQA0oqO537u535QU61abprwBDChotEcCV4a03sJXEK6Hj6Xz9rRb0xXwXcSTo+0OnfDc0L6dE/3dHsBdk006id8wifsvvEbv/FBs29dVhhsxVW3MN6bmvHb9GfvRANeFy6amrEFhxemUWkHwc1jH/vY3dd93dftNYsgg+/Gj3PT00hT4PIXp8AkrGk/n09Q0pDeI9i+01FQlCbORE8h7PUUdt/TZuh5G8Tm8Ti1se/wGx59TmD1Wq/1WvvA7SM+4iN2X/qlX7pHGrgx1mfd0BOquokgTaFcEw9PksJ5zFHf0pYzuzIFewqk1wDwX/qlX3rQdL/TO73T7hVf8RX3AiXYKEqmfQgqzZRApAnd/Gmyp7nuPcKScOVb+j//T7ulUR2EpmNq07St308ztxEc833n3O9Ngc7d8Nw5tSl85k3e5E12H/VRH7X7mq/5mj0sRZOGd87gcQuiu040PjNpt+nX3qn5DgqZQhngPcHjuTBlVESl/t/nwEHf+73fuw9waEkCmBZzk91EgkMoM5sJXEI2zbP/ofmYz2d6pmfaP6Zx+amv+qqvuscy4ZawTtqZH/ve7/3e+4ClAwLwgR/4gbv3e7/3273Xe73XHhtlguGe/Ebn5PfzK/0G3xIq4DFEoKPPplknCpD/m1vheI3XeI3974OkaNEQC4f1S3OuyuCQgE34ah63LZR3Kpzt3HDIdQHmhfeZMjQWte+QpRF5f/Inf/Lu3d/93femjeC5gZm9NJ8b6vXUgplO72du8+8SQL4qoaOJ4I9gp6/4iq/Ya2gA/fd///fvfviHf3j34z/+4/vAZD0EYj/xEz+xB9d9TqbI/37lV37l/rt8JzyV8BJ0v0nju45Vc04XpL/loqRJfS5BJ6Ci/Hd+53fe+6Tf8A3fsM9OgdGmL5pgTbB8K9GRckjAuzcPGeGckd1Ma00t2uG1YKdo06OFBQuBUAQA7/u+77vXiG4SjZPPtt7I3kv7EMa0jZvvc7QiAafdPuzDPmwvPNKPhOvXfu3X9trn7/7u7/bnkOYpRXhVQDGDEJ/lCzK3vpPppfn5yZ/2aZ+2xzW5JbJN8E5ugfPOj52+bOZ/BlRpXP9nDZh9GpXG/uIv/uJ9CtV12Ozy/Fvp04kZz79tmfObpiXv22jdxVkcN6uFmEK7+pl/9md/tvuO7/iOvckEB7kB+X75X26am5NPlilMAD0WpdOSb/EWb7H76I/+6N2XfdmX7YWEtpMxkvt289ogAdzTx9rCVw+RMw5pnWAvGSABneQA/xno7pwEOW/2Zm/2oJDO4GlaAddc0FYg5xptWpaEJoXnvs/7vM8+C8bydF1+f0b0adU23sSMt3DMh6RwuniaiHB2sWtq0muCwiR9wRd8wd7MSvsRyLReeGLmLzPn/TSM524Qf4925I8JnvhktMlv//Zv75lFtEoowAour5HpIThmgtGHwOktLeSRsNBqWEzOiXvgHKVUpTe5MMy/jea6CB5tmoUo8Cq92mNuTTjpp3/6p++hNlwCwpkv38ZZz8v7d0W3u+fC6QIJZsKYIEYn63MEk2n92I/92N2bvumb7hf4GZ7hGR6Mvgnc1B7Tx0wofU5qkqlEugC3+E7uQZjgoXz0FKRjWmKLK3mIvpdmIgwJxAwu5nclsNbqN37jN/bZITAZf/jlX/7lH9SkNiXzXYDVe9Oy5J86+NXcF5ZIUOk3aFIY8fQl+/0UyF1oyfsCSuqGtyvXmwdU/vIv//K9D2ZxaQXmjcDlf6URLXgkix7dDJqCKcMsEpj8yq/8yl5DThLFIb7jquG2SLPnHCsxJaE8hbnj/5wz4WH6XQu/GBog8CGAYLOw0SwGgaVlWyO+q8/ki77jO77j7qu/+qt3v/zLv7wXwKkp58bl4twLobxzEL4bMf2uGRUyadg40nPMGN+wQCBcsCNIJV8z7cAnJZQyRKJk32eBaYH5WxNLPeTsr9rxnIDgkJAeM48r7S1hyTd3DYT013/91/coAK6AQApNj5XInKc5871bqxCNhBcEx8UB3per95uCz2nFnqSF89STnyUHU3N1EwjS533e5+0XzQ6322nMyBEWlyaw2NHTLLQbQ1OCZSw2n0qQEQQVxueYnM40WRDWFLxjpv5U3+tUU7jS+zpX5vZQYOa8+Y38Zj45WIrJLr06M1nP+IzP+CDIn7lnZaRDX/M1X3Pvh/qemE/9/iGK4kPSrCcMszbIa/4lxjgtANaxoAHlQSRpztJ5pQa9h9TLH4M/ikYFN26qBZ5uw1ZueWKuVxEYrut3HTP3q6CvcFsC63qKrgvCrB2BQv74mZ/5md1nfdZn7ZME1iQNGYIRO0pefma3rCvz/4hHPGLvh+ImJJSTfviQ9Tk70goJhcUHE4FyHvnIR+53cVoxEHpG5l6nUe1+gQ4TDscT3RLKbmwEkTJOq2BeaqHP0YynCvuhUpM0fCykiX6ApH7rt35rjwNDJF7v9V5vj26wKm1mAttGJ5zwVNqVBSLQtC8/lM8vEGPqrwoInyTM+rlmjhYgmGpwLKaFDIcMFpk56CLxIlKL/9mf/dl7hz7f1UIygd28NPUh/25q1XtpurYyaWvgtWK/uSNdX3/3HvdI0IRIbR2t22Q9lWkKigsX9VqgJDGgWG/FZ6f78SSTIVohkauYST5bGtJiMDUWi2a0iAS17Eg+JsH1Gb6lHDYMkKagMaZ2nL+zBfEcKg2+3ytO12Bprn2+KU3XI7jsO7/zO/eJBhu5jW4dCWiZJNqU5gyKY+KB/1/yJV+y/47oiLlj0y/eYubfd8KZg96NLvuz+lEtpvQdjcnPYVosClMeLteODlDPdwKdIHrwTy1cWnJNtz0pH8c20Qo/JcilfHNjCqYETHBdFkYCwlrb8Nba+vI5g5fSsPn08FS4MA0qeq80uvPwG1tY8X1PNs55n+zszBFYR4pOqYRFoiGByhamjMbTPu3T7hdJ/tzffU6gpBJSiq/vsziA5ImXPhSPtbJxFc6Et7Qw39tjJRyCHL4oJhWXSKSeJmWZot1FI4xcIsXLQrFyfFAwVi6T750WMaG9tKm/eECQJgtbbBFF5SodCSbhk/GJUWRxiipBHF7nIyF6cNTlvu3etMVMu90vPuNdCuc0szOyXl9TFEgs8GPgPdcoInbpXwKaFo0o437IzhFsJSGldyfc1u8E1610x3sunJ1EGqzX0wzQcMBehIZJZoh1kxkvF+w9GhUYj2omO3KMNPtQFcxVONdU58Q9Jxl7+oitf3VVqICQkclwmvVUsfBpUffBPUAaCfsMoF+7o6xc3PtCc7ajY7h0okx4WvRnf/Zn9xxGgjnJCWFuhJW5KejhH4E2wEzSjv1e2nLigQ9lwTwknGsvKeudD15w2hrReEFQPivD5F5Yc8FQ6eDy9EF4hNbfwVGaShBsQj4x6pn5O9Qj6p4K51yQXtOaRXpMCpBcatFFM9cRZmc5Lfa55/xLTBzEXoIZ/3CSZNut9xokvus2L2szhbTVFryzJhkIqc3NJ6UskGpe/dVffa8pUxppzah3mXqfA/nhoa6Wa7oQYbGXsmo3hj1WdR6D3XOMGiQOpFemu6CnZgLhbpl0LCJQkdyx7IfvtaizNjs/ay7SqfUwD0XhXDvxzWNyB6avbj3dGxUF6o9mQV4Jj6lIqjJF4fN/07SvLXEu6XfeeNFWgU1jOlFULw0M7MgyEcxEJqNgqDQlh13g0y5fGdsFWgVB3Zitc3koCueqGQkJqGerr9LMxPXZQPuCVVZJbv4pn/Ip97VTlTK7LzRm9VfunwBWBC8jR/se0uL3hc85KyFn46kccJkKwhaBo/xu7PXpeBPOj/zIj9xrTAsWVWvN8Kw9Lcs7ryb//yfhbMNKSBDUSMTTN137TbV21lktFJiucmr3o2yd5/Fl/Y0GxWXQ0qcskt8o3TnP+Z5G65OUOlv3xclUYMV/fPqnf/q9eXChFaDNDhs0KXhJRgNwPDvDrcyY1bcsELuLbMW9CoYmVW/dqLMylVBGr1v7dm4x8isVoUhUHPBBlXRk4dyzSeaOUCKLhLD8Iz/yIw8WzkXtC266LwIiF1r7k9Q6upoMkAuNwFG2x46UriSQ+ThaBGLEyPpMHmHPj4Hs95KlfVepzC0O6YSJVsrfFtF5+qsJ/Myb+xsMWrlzKIqjUpAqPCVEKBUwHxYUF2xinjTxKVzQU+/ZRWCO0llOVJRNE9YcK7M9+YRlIYC80mRoX5O7OHG0Y77kKZ3VTmn/fA5D6F42MkuwJhd1CtihljGzdffUuLMLCDMtI6SsmAKZPNqeV9HqPZ9TMs3/TA5i1fe9h5TK2r/g1jTnLJmV6gIbxRWMnhW4O9ntTD5nHNQUHHWTaO8YaeIqFvpVtLab4KrXpcoda4Q7Sz1mVefaKmZtmLv6nmtZMHdMJkmbG3ECM54LVryQoqE9NY0ASxUgzWra2btpvZbJ7b014XQSHHEn4gSVteovySQU9FTHUt2PCwa0P/rRj9639OO3HKO2XaqH/DEhPCY0s7bmEv7UIWjoWC/1NSs0Tf1V/3eI0T//1vq7lwJZ7HiRORb9bPTgUYCbkAqi1Gkx72sqdWvwwrm0uxs76znVqP5Uve4Vpb6iaVXwXw2QMlUEEGSCHPrpE93VtIcZ+R8q05h/vwRUsuViHCodWctHLtFucP3/mqMVIFEymPUCWi5YTRpmp5TSz4IjjCcxhv/bwp9Xyt9Wr6xbEc4yQ3LftCYQvTxtGaAaaNVpA+iLDFvj/kgDEzS+JNdyK1JdJ2nMTh6XEsJD2v/U0uHogIfO6ZSiuUOac96/GdT2XYoNdT4RrIKQEsjYS+GgCS1XTlp0tg7a6iiyYqEXMeurVptjUzyKtlGyIgm7mMgcNGZmwYWJ8pjzaF0JS9HjbeCEx8z4Vnbpkt2B1xEyx1qIr21ujmmZiTPfBGmZfIiCFO8x1bJ7glau2Gxckbvmvad5mqfZE5R9NgHvWlb3YhXaqxTQtZz6vpQ5kP8G4jLnU2NWXAU2ssMIqQpJ+BhzHv9wNu7aynSca6aOaflZs74F02zd/JsCysd84ZjsCXCv17Ezlzbpa+S/pjo9BwsJVmGa7m3l1zUc6x7LLAl0tQvir4Z9zvLvNXlwq2a9xeZrKsUldDX3TyBjsFcDFGwEaE9A8nXWfPAlfc/Z8qaUaKbT79doYZr9Fey+qYAe0s5uZEdQ2mxutjXC5dzzOJRh6zdmkBeRuPvgXHSqEyPkb86SmmBC+KdKBf1BRfzTaqzXfs41XPsiXQjVL7LTF7L+5fWKnKwWOw+XE6ulltktzFb57iWB9VnOsTVxY4U41qj8EtWHW+P2/IaU3xTIQ6Z/0uYOaaFTLMu0UGuziwkpzfPRLcXABNoxDu7MGrnX6I7+/kEf9EF7ZTU32BoInQPJXdtMMc3qeVT5ReaI1VIzrRofaC1jV9G0a9vDrU4cN2EZbfmSq1k/FByswnsJ6Gid8lGQM92KWTa9ZnFW3Pc6mnMVzlk2vRVwTSsGXsJ5cA+rku3+VuJRlSwlpThOZe0cszMnym3N8rx4tM4fEXXXVKuePLN1jAshuNrD2IGzU/FkFM2Fu+kcm1Xwp19Zik1GygLylx3M6m1R7laNmFsxr9F1g2JEyc5LtkYhoMcgmsmfncys61AcJwowU89rBqfXTDW6HOrjbHtTz/ua2EbgKeCdvuesKTsVNrx2rZBeROp7ak89+2ImoLIIcDDMl7W77mQ0nZPSOldAY9ATSAQHBBOZKabKgkMalJC4AREXVtLspaCk+KkRNMIYbRDBBEuEkqahrI3P3/vFX/zFPe8gmOYS57OmPyfENjM4/Y8NDfvEiGe+Zy08PLuhYZSR+CMrOa3SVoOGG0FJK3TUjeM3Kjmlxic5IJihhq64nGY9CoK2pvJOs3kJTuZWlziaiFkijCJKiQLQh3ODuXJLpOEIBCSBEIczrhrupsFQ+We+poNW1K3EHExRseyac3JuqGle62oCDbGpEH0JyhYL/Trl3NPcrlDeFFQH866XVfzcrCN/072PdaY+Sb087LsS8WOjIU8WztUnWCPozIASXbT9OUAqWhyhjDCgDoiDzD+9JM/vEAEleKu+koq69FDSn1NdUn6SQwDnPEEhfGNkB21xZK6YVEmChH2aqLlZz5lG0c1xbk0i9ls2b1CNqLcjMjbLJBOjlhzRQnPZS6ZT1852W2nVtLZNLrAt0RIgPyeGcONYSywnbsqUo3MTHJvCudYjT6CWutaAn4OcIFrYRvXlk8A1LbzOHBFRb4veNs+7ZrQETJZD8waCN9sp2vm1tpklsrIhNClT38IGOa0B1DmuReY7jcVMc4vcaBBM3NY5lKDans7P+tKkNTuYxIpLpnQP5fR9Fjoj4OGuzaYXc2KdR/ViZnfS9FtFcNfCOQ8J5zQDmEecXm1OisgtZrnzivU5z1//9V//YLHbbTWEmkFF2om5RN0DbdjJDbGqFqZ6psgMs28QjYp4yw9lQhtWcCqVbqtH/Cw58YjJw/LQiNavNjFueDeYUAbfNKzAusIcMdH5qZeeoLa6RTNw9V7M+doIlQmcwlkQrAqCm7Ra32sHRKtwzhOs/JRjTPAsbDw/JzSn6jpxPpR2KNN03GbHskm7Y86NVLGBMuOBx7P5bDhdAuFzT/EUT7FvyCpYYnoJ52o+T5k4t+bs0+p8YE0i9NNs01TGEjWtQVwhHplLwuCzH//xH78PlC4113zLBencZ5cP16XBQti2jWWzT61ZqTGLQDmtZSPXxjlTu3P0ymTGWFg/2Al1o+sAV+4VJQ4v0IWsJaOnUNuu6zv5XppajTXCc8OzYtdEWAj6ihBNW/o7s17bRVGnpAH/cPqMp/i+UzDd1ITbczPe9Xyqj7v14g83lS1opkKzPkOYY6Tz6bgs/OJLd3xbr2Feh7+piqUR9QK1bjX4DeMOZrLpQYhhnuvUlJOFcys7kSM8L97C2rWToVIhfv4cgUBWjau5xV289GLO7+MrqvqsTt651auyRWyXl5Kbza0IKCHx/5o6aKOTOb4qANnq/z7Xz8YBFwkU3dgEkRWqbDrt3ppm7ptG5/xFxHw68NdttSOcad+Qi/ovKcXhluQX5y/PGfQ2mwCThk/rzvLua+Gc03Et6u1vBUKdwDoV1012U/lsLqACuC2NeckFnT6NYIPW5lpk0mc35Oqyy/lPoUgI/I9GAqJjAuA6CmiOkUtWOt6sKXcQTq1dUNEIZ65G/MgEsRy2G+46gmlyA7zG7urcbrNmP6FinmeXOTgs0153wMlaqpsI3xTXM+uz1rtfC+ecROJ5450Q4ZvtCgsmPGrCBfLQgFRQUg1733lbjfBntknABgQmZDZLAU+ownRJ0lBhs/nN/s/CY3nD6wpqruJJbg3RmjeYJdH7CQmmQLLOb7kTNFH9SIuIvR+60IFDKet2U+E8NQYQDM3gBtpA+DqfNllunjp33aclPFiztPCkJF6pOQ99ICe4L+Fr8JXqb1SEVraAaSKc1H1TLC7F6jk1UeCiBUMCDtWfMaNKs02TmbYvck8IynipcQI685un1p+PW5PbtvgBbXZrSKvbwPDVsiyVPoQY9P4cxT2HYRFsMF0b5xLCeRUCUaPeBIu55uJlwoPDghe95x7o4OI8pwW9Mdk4QkIaFMYFmumGzmAomMPfRHJ2yszZ3kUJbxfKARcsiLiDZNpQHhNU11B9U1orrNbiqo9hkrgnE8WYAPwszz3GDe01ayLTAw6iWZhs/vAczVJ0XgRcQJd5b1Ibs+7cbruhWfctInHvw5ERjPOXJ+knvJYVgM2CzgRvcw7VjYgfUw3b8QY0Ybu3m2fEW9koP43WmvS0uxDOeYMsAiyOAFicprrNjnaZobRqz+eMdYuq9MD3xSZaKxZnHv4Y33J2xoAAAN+5DpPvOvHMRrWsQREN69HG0zezIQ13UcK8drgjE7JvYMWUVD5nhGTXwj2iLCiNEItTGfxHmdL5F0FI8r2NESlaL+HvtWBJr/eyNHc1jWFqKxcvK6VAi/bjz8U15YcGfbjRsajs/poIMJlqoZjNGEGTWrbyFFdTfkw4fZeAzYAr0FBQUTBcBIpJopn923VPca5y1woKZ278rlrjlPFiTaE3yCCQEOucOzKVFoXAPWJ5/e86hudk4dwaLOoG8BkQJ0AYbl6mvaOxdaJ0IL3/q4fRvRhfSNtJQfJ/3dx6f1rE2nnXm9JiNk+yFKcF5/AHgUyC8ASpj01z23qv9K8MD/+dT9a5BLSHgNSzNHekNuVKdrkGhPyuGj+sCqZ1EHwipcBp+dBtsPzkXBQNa22m0sGncgI2cbp1GLwAR89MBIXM0Zzz7STsaDsEz3Or/fNt+5prDteGqhe6G1xETFgruss98ZxWspAyGyAk/z95pt2UldFzTHOtJOMwQ7lxJAp5f9pGkViz42sJ6VwaTR3khU0l88XfqwX5XQnnSgDKoqq6tWZq3OtNkGuSRTD1GRHkRj7nFnrvRpB6N7mOHTnwc5gV3wKEJFq+TQbSMc05mzNwK0TaBLTxe/lErmOeO+GlxbSYBm6bbxQEFmlja07mKVFufuk0Zc5TMNO5hRcW6U4iiJvNYskKgbYe+9jHPrg5WKe7MukpmtnvU+CLwyCb1nCzWiZWiUtOkGlg5CvB5CoNemWlIEgoxzeoI/wt1e25rBBtMOlxd9kzc+Z/ExoCUfTOTzOzfBI8LCaNj+PJbXGdIJN2d75zROnZ0voUwZx0u3meMZ2YeJAM7WNjcDlo+Bpm8X1hiVwAGx/LZ2Zb5kid2z6m9UhGyAbFxX3Kf55jtPPrYeOs0YponM3nXNW4oEA6EJRRdJuv2SQGu9virmTYu2p4tdbnJDg1bMDgoQ2lI4HgtKOgBLnDonlfZF4ANDtuzBqf6zD1txj+aeNalHMhpDVhoIjH3CNkbskEeWz8WZusgVWd26E2Prc5WW6FGlkAPmWaf7ZULz1cUNQE51MrMa/sWozFDh7qx1Pdjpx2AQWw9ZI8w+tyOqdgzVEkTKBAyfXw2RzSf3LnhDIewZobX9k510Ee1h5HE4YqSGAinYuNxB2BOHiPJi91uhIz7mrMzVYjs7JmNowqgvDO3JKaLlTCo8W3KoNztP1BTCt/wK7m6wQQ15E4zSlKw0KSLbCY172BlxTQyiy6jhqrJhxTSKbwJIjxL5tEsdXE9jpux6TP9Zs2jBs8oTevCeWsCp2UwFnycpfCuTbuTQsiIPOb6/ffTPcSM943FZplnR2QrxTOQ+PsEk75W3BBrZiDkQKQRbmiNRkLwOypSf3b6me5juLLjM7OGgmG9wgBn3Jt8JBQ3HSEybyps+1O55h5n2XACeNakNZ9qe3kXSiBQ53ppnByP8Qk9SoIcejwnloo/mmb7mycc0s4pZ4EE5MpM0kfIAREBlWDZVNui310inZaWddbvdRbnIKdKZgrE3xt/n+dZmezXn422519ouYcoYRz6/cK9FY64103ss0SeE/TWUyr2REk4nk95sUk/Oc4qGc1j11LNltM+JSqxZzbSn/TnrA4RAZ+aV1uz0nu36ZwxoqalYSVXUxi9WxXkwswuZhbnUDOqc1ZJ4Oswj7LYabJT+NPf3fWgd8rEH5agRhKKlincGZhy7xBRHyOjMyGEScFRNMHm2pXpA5EJf3Rtkpd0qB8TmlLu4fKXrvS3WV6bS1C26pf2SINl57Mz1ypfdcZnzdv5hTurRu99ursOvqftSjsrsg0xzJeE6dURSqrlvKKRRWqww+lWXFZwWez7c0x+XjgWB15BGO7gnBWEhrRmAYlnE3DmNzNeyGcW0SQLY06zePaE3NLCE9tnX1Ic14FyayvD/msx/zZu4Tt1ggevg2tqURjlmsknIB4vunsMJhrcmjTH4wqE1RdJ+oiV6QeL7KAiGZVzDaHsc4y3ftxgNU6PGqdZ/5Qn6l5Xaxz7TVq7fQmwLSKXRWMRDC9hoULmBCP4bWRR9Kgs1HuHFV5kJbfSUzhLAqbpF2aU1saRWWzNntGxPfD6L+1h9IhytvDwnl6I94UkDJqQHwcgGSkuvaEU/ID1hn2vI6rWe/DwR3SSaDK4TauwlnuVxpQRw1spJz+Is0i0/tFOCd7fZY9b5VWPHychik3FRojLU5q1jXhlKjRZgeik3CuQ2W3Oo9c6VvI6XJmQUaRdmdRlh+WW3WCBRsz23KXKbargoS1j9KcdPZQnjx8W359gWNVuRG1p+vXnFOaE1gvQ7eWWm8pDseVc28STmUFpS4TTq85u8o3CGdCmeZctfBtAsSrwB3qA39o1MrDx+nBUPBaILwycOTuskFlD4tLWNeEEw/10KiX9f4cpMulttG6mHXC2XjjyKSE004hnMx6+OElZ25fNWxgmuh1ZN45A7EePk7va78KJxqfatBkokCoyJ1wMuvYV4TzlPvzBD7nlnC60XBOAKrAZxXO2ON8TtF6/MLbHpS6TlVb26dcJaAPHzcbX74Kp2BYQJRMEMgIH+SFcCJKY1zNoryTKXNbwulGQ/XhmDUBWIVTJCZaVwBXh4/bZsCv+d6ZC5945aXGtTysOZ94rtBMXyooBCXVwa+S8ZI1ZEd5CUogKOls4TyUF8Z1hGMiwDLhs9C/npKElxBPLuelteea6Vkd6mPa89Rxdg8FiOdYZ5VLtDLf8tlxUWWIZluaGnpVZ4/JL0MUCH9t4scEWCXrof8VypdTr9679KUa72qTL2naVy7hOu1spvgmbhnReGrStT7qEuP5Lp0WPNY7c/3trYkY64a+jUZfKwlGdrBx2CVqZoNZiA6sXEUC5tq1m8dOkNoNpbIf9ahHPYFw1qjALhEoIX7AQyfx49JZoQB9QH9kiARwCufWANAVQ7tEkHZXQdVVv7M1yvrYqO+bnvMcKzl7aNWapi7X8TDIC9dP3KJsfArnVePKrxxcCiJSw5JZjwUfpEQ4+RM67vrh64z0OIWkSyA7BF6xhxzxG6fWnKUV5ww6PUWLHWo9c6ljnZN+bDLwsdLurRz8dQR1JdSs95ZiIgP5m82hysTTolw/Ofis65oKvVI4t7SCUl8U+xpPlTeto4PMkcKx2tCssyyvOztn3oQJEXmUw68ufjLMZ+3QnFqx7vR7Qee7biZrqwX2lmAe4rJuDeE6Ny6YNfurhvaoDksXkgKitXEaQdXpGB56DqJzpSlROK84qe4Yc+ZMnTOUroISRGITfD+lZOPQos0+6sEW3Abno6ULjS4z4ZFfrERV8IZ/iohgSgX8DfsazIXWpbpSQwPPL3HQBJc8fKfzd44O5zt/x/P+5nPe65p91vP+T75bl434k6EvswX6TUgf09XSfVAropRW3T4qbfZaNG/YQk1ory2cM8wncLJEs3nXZMLTnpotiOhrZnqqo39svHPls3NKhpIRSQFaWrrs0Y9+9J6ljwytrl5E6FHLb+1kNCDwmfl31C1JBUEcP4ivdN3Dd9zk/w8dggeH89TzqaPz9TePXvuMa/N378vmiQGklFWY2pzcrYr8YgOdajVWRGT+n+8SfSvjUdacXFR+XYaI9mR9pS7DRm9UppGfYueBCuqGNpnwVdf5cYuigKkA5dCPHxolfSgVGe1OeawLNAfHZqCtPXcj9HCyczVL0BxBDb0b5gbKTCi+0uqlYK75nNN/PnTMWpjbOI79jvfrUOKoD9G8jv6/+1ITLdfLD1RirDYeEXzW0J9a5rxWFoRhV+bCkgmYJwBfi/MsrOpc1rfxkteepjHJtgmHiF0jUIsCFrAoU4PWCpqJzYysc3u2nP6ZxVmn5M5zsONob4I4m5USUuflJijcd35KVAmo89HIy+vKmmPzhzzUy/6co2Gzt3Fs/d4c/eIzAtN6x1fpWD/5ms7WANf9sYGV0BCiCc2dGqyu7Xhmaa/ghmYGI/ntTHgRu/NzDQZH6BewzpM/a976lnD6AifAfNCQAqNmbSeYBJZmhXWqXc/H6XEFbg91AZ7zjvpti6FXE2KBEuQCMwtA8DTOZ95oT9rCQYN6TNt0nvXwmT7zTY/ZJfm6Rze0Y6vzcg0LgmjmWJ3ZaZrG9R5hhUH7PM3GBz0UGF6lOWfn6DmHk0nn65ON2jN23tUOOdwbZTzntl6/Uji9x9dD7qCepaLyK9JIdimBUB5MkGb5wWqu1y7AU3vOPPk8IAYaiRHOyKw1VG0MH/MdvFWDsTl6eQpTprHruJ+O1a0oEzf7J9UUN/ZPAllBWVk8MB+hUTPO+q0w0il+39o6ZioUFg3TCOOoFoizFXuaXOWlQO3c5MdR4ewkNFbQ1aHZM/kV7VgnQTgFHkgAq3Bu4YNbraoT1imYzocvm3Ba7DQMJ5ypF+iAs0ISZovtKaDd3KmdzhGcKfBzltGljkPfnRvTcIg+4716j9b+JVeAVakFoaFmNOdW545Tu/hN7Rmsp2kbNhKXKs05G+JGPPb7XL5zR/1sdjOewukkmGo+n/r0uszNsR51ahOI6IvZ92xVDR7rn76mIPsOEASmNV8yRj6Tza8U9GC8eO495zEHTs3RLt3ofLyqBc855tCA0nWXPvruJn3UaWU2s4ieNoXT52gw96iZSgSGS8Q1u079/ezJOXskCa70n4LSuC9rg7fW1t9ATbXGPIcptimcs37da+A6jUg9r9qoPp1OTFc0ah4BZKvsc0tAD7GgZ1MD5kPlHi3JlzRMgBmHEIBz7Nz8rAKItXn+nNHoPTex/O9VR9+5dZzy/6d893yeQM7AKO05ubSuISvRfZi+p++wYUXKcw7loXaXVwVGM61NJuCr7sMcc51s9NrfKSwK7li26mzh7MvgY76cYz0nduXbTUfeLtUkq4zNVkS+FQitAloK0vnA6fi90qj8GxqaKfdIQPXeLFtFc4pQpcscsL8+77XIkrYl6P5GuO/lMTHT+V44p8NzQd/EOlkLbk7wXvxJm3SOK+SXs3oNXpj9oc4NimZShTVDHhYIpymnv+k1oXXOtDYUZ23wexZlbks4uyApQ2Cri12jRifnPf4ov5O6n5WYa9Bz1THz6XXhoI01FAMbCYLsSBCFG+SGVN9EAKXTpMoe//jH730dzjislt8lq8QKCBCw9z0/dvifrfdloC5x9F3OpWP+ze977joc3sOdVRX7mMc8Zi+IjerufsQE8mi9/H/g9/Qdz+nNOS2ZA+5MHgp86tM6gyGuhR5J4d9b9LuzhHML40pg4GW00AxKJvhLc9FQYAPt/FwMLGySMfqdLeLGZLbPHpb+rmrPLEWBjx7kdqzftjuDi+xW0JIRJHA9v03rOheaQ3tB79nFAOGed/jsKcf8n6sOv3PsAMcwkR77fu97dH7el6XrfF2L17UJaqBsDKA5ZJZwIIJrp5iveF264Gw25jkmEkUQYlNgHIJQUZseqGntOeH5FCrf0Tz3ygeUu3WxTc+I05lwcs75f1KHTDtm/Jz8NVNnc+DnKpwTUoqJ5MYAcglfsEoj93Ivav8tz98AqbWH5YxY74L4cZWVOERJi4dasWBaK8Z/w7bmqJ0EpapYSQjRdP7eqSNWtni9c1iDbBPYkOWac1CrlGjiHJdEutnmW5uAnRUQraZ8RmktDDMpr90JNdm2hSEofD7a02ft/tlUYWXOzF6aKxl43bHeR+BAfG74QEBv0FYbhs/JjK/cwdny8LbrnK5LXq7Xe1o9gSr16DULgD9grcNA1/II94W/h85WK/TrNJtNQWSGnRtN6PebMtcc+4mMeC6/j3xjva/T3O1gk6apghvQalFkgZjUfIs587CI098tSoNDVx7l6jasZRXzBCOAzEa2RbpzQeZQKRE9jSGnXF/22WtzwmWHeJLncD3PEb6rvm9qzgZKOWcWyLkx6UwqWG+OJSzJ0Ga1cQWwlETWa1LezvU3ZyqZ30vw/X6Db/P7WVX3xD3ghnHH4luc23z3SsrcHATgR+wEzJ7GpTTEqWg9x1hFZoB87ZknKWQdl7ylQefQgOZvqlXSrLYKv1JmFmpW/XEvdJiwmPy1usfNDXA/dSJZ+/EnTHNmu0drCqGQrZuNs2L/BMRTEDYy7dtgqut0Zl7bfcsAGu7AfdInq/gjRRU8B01QvhHn9joDvU4aBDDJvvqVg3RgmpxeAUklGzFivGZaBUb1pyScEV8nuWO2uc7/nEMDZlmA90FKAfJyx9AD59AMHMJpgQRnYBdRud3b5spEHdNs9xP52PlmFuPWRkebqU3XjwhTn36+OeFIqKdwniugKRPfAyng69abNX8/1CZtLqNXVmirM/KNhXPmwuvmwblVqCRqT6WHdUb9IiyAcpkB0WW91Wc/9NmYdVZNZuLnhqivu9c0IZItPDATVk45zWmB3CD4J78HOYFLUt+mmsre5aiUU+uRZpvtNmhRuiDIhpslEKElTYDzHq2KKgfCmdPmriucaU9Rv2Zcvn/OFF27wFAc3DpY6KGNfzbZePU7Z+vnfDa7h/ZSCjqzEh0JqHQioi+8scK31VyvOfWtiRP9fu0VCanv+6RP+qQH50e2SOVzm7Tr/MApND28kHmPuFz/+nutMdffnmUmkYN1ycD2l0CIbVU2KUvVJDrWA2jP/RL8zUZqN0UobHIEoHzLfNtMutdcC1ob1u0+Tf9+bsBVk18ZrU+gPOb0lPBMsL/xZwhgRIN2TVAGs246mZ6MmdXMVJHn9D+3BLX/mdmi4BQlCzW1jcvYfEgLxNy7Ud5zQ0WXgoMGXk3f7lBz2LuYET/XYSXeeKQxCQVlgMzBKvAnWafSl8E3T/7kT76Hd+pJ1JyjCSFtCegpjXA9CnB8f5DVbHXYtBWkb9UJLKzfnm3PV3jybJxzncMzpX6OPOHPwDz5ObSTxWpH2cUcZjgXoJjvQUDnzZh90lce58wgrBN6O1cmi+BzHwhjvk7uBeHMH7OIzke2QrZobpYZmJ0yz/JY9eMpbPJDfv2MjoNvuCLaAQkum+4W2btAMMKFNaAoCLEsWPdwbSN+le+3To72PTQwk+67ress2QmlSUkB5jVPgBC0OdZR4KeiBpsLOUeJTBJGILr3CYdMDN9T1kZ0zBcpMCGsQGA+EtLGJB60aLPd96xBP9Z2phttwUBFzDs2POG0cIRRMiDfl7aJLOHvbjQiAgG1gHPI6mTdTP/40hp0dW2mf1nwyF+jMSkAmpJ1cMzoPKIxofBIGQhC67zSxttqp35OAwWQIOTDfZ7sqPDttKb3ldKA/GZfgakIptY8eWDBPPmEc2Yk5ngSfyMc8sBUuHod0AEtZocTUict781PgrfRWAnh2vBgZopWmt2hdKrz4tM4BwJHg4R5VuMU7lfglHaRl5dtEv0GY/X7cxDV7Cay1fLlFFb5Vs333AiTWBHz36hDyQ7rZ3NNRlUjowPdbcLKZCiLph2vVu+Urn1b7zsfiAc/1r2N4FH9GAVQ3EEZIZlwB3MDVxbSxJGv4pZutlOekfWsCw/aycmWouTfUPecYCQDQgogdtKElO+JqMEE84Oc+ASZZyePtdvteuKzfrqATfkrUFpUHk1sFoBl6hPQaqnlfVVwQh4EbbIoa43LyuK/BC664qxpahF51aUSCDUpiO7Hb84qTeiGNoX7+h8YZOyf7tdVfTYPZQRn3wK+5mTet44V0lU/pPwXA2mC9qdAVGcJ5zQHMxjJHyzSqjKTZqSN3HAQD79Dkb3dXKUkUmot8OZIlTTUhI3WxvVbI04SVMIOe2XObAy7e3acqBBslmSU/rTgUq24AIgUTClzzyq06+d6rAmCc7siz3Xt3AU8tJ3UrCATwN4cSd2kZ3Ms5x6uHAfUc0JBu62terbm0K+IydosYc2jg6/c0wrmQkHiN5QAEQjJHvKTz6lTOmrWt/yqGaBMrZlm6zXfyM3UiiZtybTTonEUCQxBdfLeryWJ3wsqaXHSqHPM38xQTBM7cVLfR4PS4syPGzYZ87F2MoXew2yKFe/zzlHenn/Ml6VJg8/OTU8eE8zYVr6fUAos+c2AbYmNWYrRBgvLnIMivLbxBZx8aPhvG2ZG6OswsBW7npDODDptUHCQNfE7BbqB/5Pw3Hm4B6dARCeD8Md6c09tMVNQXVg5d/4kWKcAhCBKcVpwh6CpMl03Aga3wkr5KBZ2jvVbTeJWjj4BpUERYOV9MzduLGGcdfZrz/I0kIjeefNhsW64C/BRwso/JVDOb2rVY61kWieYKheI2cWtlILV8EBtjU1svWb0PQVhFvTF4g9Hdp6YYgKWUpSTfbSyn+YGz52adehTsAiac2ymZa5R/bLm3HpBL35pI8EvFThu7vwtYHw9MvcWBcxAa9lB/DmPBLFSCqaT70kziPhkL9xkApX2bOFypg/Ru9YGV+tnCYFgh4AmlLHDnVug/QySMlWTQOJc+X0qF0WguKw2IZ8KXuqa/RaNxXowZx69RlGzUdxgn2VywSvMNoF0btCNyhtmzbnzKuioDjyNHwOI1ndezKgNMzf41nz31TKu+O4MRK0/rQlHJpgxv2Zbw8x6Zh7p2bVGTrkUb+GocB4awTHfjywLW+N72tFUfaQQoK2LZDaltVwM7WSnuZkE00XlPF81t2g9vwnOR4tzTnLAMlR8UAQFZbJudqZzBkiZzVk52OITBtchG8V1oSX4zwKwRz7ykfvsk99xeE745JWZQ5qNILIcghablkAGYocNlmkJJnLOjlkGHNtdBA8hoYElFKbrMXkQV3VwW2u5JpxnMzn/sk9V2paFaq1YJ5aRJSDQpZhvTXNuNT1YhXOai7QfKhfAmJni7wVzBNITDBfjwggIN6DUZoylddcdCza2ougZTAk0MHhAMoQqdvZssJDGzPcMtysdmPBUXDbz+K7FtXEFbEi+tkcmmgDZiPDJ8t1NHnHMltSZ677fd6fl/Za1FIz4m01N+1IENPWEi2ascEgw54iVfNEsl/UnYLQ+FMM96rqdi3OK2JFZp/0RUQSSM4FwqV6gDxzrD7kK51bHjrBAF8nMUfHA7qmBMpfVVlton2HewSdbszdnScchMHzOMZ/+Z1Grc3ITRfIqR4NeEsIG1icIzq0sTLzEWY7bnB3fkZDxuQhP/1dVZ1zHhHuW/E6T2E2PSJGG9Lpx0AQcwI5MYY2nkB3yf4+N117TxmlM3w1RoeWjwbWRoui5PufstYyb+CHOwrkNG64UzmONDtYuHWuwNGeGZ15BS8yem95Cz8YA5eFpCJE8lgstlxaYfSWv6ti7+lNbwHjMcdoGqkCzM61gmiaEEAKLXUfeztkGqgFYAuWzmebZgSPtt3YUCQaqRY7/7/2SBmXUAtSdl/NzbjBk/jyoifCEdJTiXLNqa2C2rt/snTqpi3xllk98MKGiOc/SuYUgVILhfGZgdSmt+UTCufqVh7rrzqxOAlCCXyDgpAVDTYyNkNwNyVRYBP4Y+IZbkOab+fZzJvXObiGhCUFTnksCCCL4hzYGBGEWyM2Sh7Vr26yVyg+b7WOCV+b/55/lt/ZbbdaCs2nWI60IxtRCSWGKxoP0QkjmUNOtAGjNaG2VXszMHL9RNi/XpfXIakSqyeVg9apNmpnESxK4HzgW9BxqwDWFM4FIkDwnoOrXRZV1n6jbG7NAK2T+3Ah4qMURWF2n8+7avD+62VbtUlpCmk3gwqGv7j3ySGa+qD4hKmMz/cZu5oSlOnxmmvWpWRPy3AT+MMGVTcOgsomsx4RmZmZsar6JQZ/SBHYSe8BcrAoqHM1eoDhr4T2nzb0vwI3MMzfFGpxexOc8BBVttYrZiuyo9fC12O6iSNGkmz8rI0spVp03d6LoUCqxHb0y5k9JC87udrMNd/hdAuq1iJ4mdZ78LJE3bSUQiMyQiZ8dN6aWmwNII1xP4evR+wmhTZnPWjkFU+r6ldFKUggwnN/aUny2hFmhoa1+A6vLU8p4sq+avkZ55GOv3e+m/02RcDFsnNCBY3yIGwlnZIeEcWtM37GgiTPcIqZNfYf3ZS6QQvLl3EC+nR1aSjETJ8rlYLs5fMQySJPDudK5tqL3Q4zvQ/xNMBaAHfQEyxTdSwdKwWb6aVba3yYqiCqIKdgLp9xqk0hA6xvqOmG9bjI4SoM0KUKtwmGF1m2ax1VRbN38NY8+PzOrN9eKA2iJ63V9Xc9KHM/tcH3WAzBP29ar8zbnOz2w8hin3zbfP9RwK1+zzwfoVvMiwoRzZib5XY6yHR3MhhsIXGZmKovtN0u1rY73GgCtQnhIOLd6RVoLvwtgt0mcO61Cq8E3UfNAR9wV7ojznb7m1JwFOT4DYqoVtgwZ9pBcvq4ZNNChm3wq6Xnm7LdKcP3GJHhbR6lT1+Z6sgx17sjKBWvVWsZGsjZVE0Tcvq3jgVVDbnV524rgJ5l1pYHlJ1kQF+Oi5NXzw2rKkFahjSaeRkCVJQQJ9f2rdmj3rsDvoWBgbajQjZrXGRRFgyGpaPOHwiYzJEMkpclfpWUdNIlaKXifw3PvEUCBnuEBtKINJ31JO/pOArNWGkwtuUJrpxCa1yZsK+YZ4cb5mG5Bizf5Ioy1ADBM09/gthIMXIBZiXuo18HFhHOLabO2KJzCOH3BqSmnAMwpGHxSKTx9deImVucTo3s2fPWaCeWgW8TyxlNLJnz5vVtc0KumwU2MbwaB6wLPTQik5nLwVQkYy+CghfiJDs+9J5IVePmf6IAz7TtpZZOUce4NbK2n2Z+1+bPClTnmY2Nh8a1Lm4ZpTuShUdQUhgANbzY/c+3feltlLU8A3WwB3hM6CpZZ/aCpoYIUVr+HBrFbAbxMYrS1fDj+msXyNyaeAMPSaKqq+GYLm3Uo/Slg9NaQhNXsrxmXUzuwbVHq5hyguRnWaHtG0GtpylVsKKZ1LcOYwl8AmJJ4xCMe8WBqtLbc4oAGUrgvYCPvN9wKc2r6/ly5rbz8xc36Fra5qutVOLcKlNZhA6tPB2gXdIAh8nNmEDG74RZo2NECKkQOmooGXWtQMv0zYDqUwjuF0jY3X8ydjjVdOAV+XbvZD2qmDA/5lWsXt+uO+luv3fqwPjrvUQ6s10wY0I6z1Djfk8ASZKwn4H+dBkMOZjeW22rt80Q7fwu6WbMKhwKKeXP6rumbuBDzD6uLKSKceWa55PLXT/VUT7V/BNTzW0EY9f2Z9eeTFzqJwVel0Y79vWveYuVvwVVbnTvWThdbVabHZpqf42/O7M9UCLSl+h8akFVKI0YlrMcVnLX7QbPKpEkAcGE6L2td3dWEp9YmwBcXztXcbOFoc6HX4asz37tlEtMKNBAzwWQ37rgm+ysAXqPaCMH8UFH0LDedvucWc/1Q86o57eOSOeFjQ1G3PpsfP8tg1rqjq+p+8rubCRo3QRBXfb81lPzIpE8lEOgeV9O9kTJdLcGqobMKM6V9SRP/wPziCSEdCpLWmUGnNrxPY9CeHGtasH7itcG2SJP9Ar4oWGJuLCxIhyYQ+U6293ou0wpsFaedWlW5xdg6lJzYYlEdm2J3yP89Vu+zaqdcqVwbARgzDjtF2Ssirypg5WQWkBJUphzziRsFVdhKhW41Gp4JkIv7nCs8NG/slnAe0zKHJrR1IW0EUA2SCBNfSXGkkFg5s4NdYLfn8EajA0XzouPKjAuW1mK9m+zmY4K51ZHuOgVv3YNDc0C3sNw5XMI9Y26ZYGsCzrKJmXHBTeSWiCWx6yNjl0aWW4ft8u9rnnaIhL5a0FsRzrnjpwad2vNY9uUqsvK6sNXQFMUzPUBuPmiwBo1pAZ/syZ5sv4gWDvDdhAgLbmGlG2kINfGzIdgh12KdxHu/TQw+xR9eXSdRuPXk6uCvwoitTWnSGl40FiYuaiW93CpRO41Z46/Ja9hy79aU5XVGyJxMNt4qwprg/FZpxGo+r7rpgd1zDEzEAxgagiuY6amf+qn35iaIaQL3sx69vLzyDzl8nE0FWQKmSVw+FOTdViOu63QOPrUDx/T7KmQDs6G6VU7MCpXlibwRD6Cy6OlnWnM4JqhPVL4GaYeKH6dGv41g6InIxmsp8MpM2hLAKZzHFnllrJTd6TdlH+R56xxStqgFTjjt+GqBMlm0LshJbTy4ij+Kgjcj1xz4mUU5BOucI4hXNYe9jqbeciVmOS8Tzp1RToEsoieVLM4cC9NoxUbHJJhR/2hU7H1WiyvQHPTKZK5qW3iI0nhR4sc6ym/m1A/5Wue00lv75Kyww6SE0QIYQmAMi6vuJxw0GlrlHxa6so9obN6jPWgRuWtQyqH6mi0BWJMRx4TwmEDNzXyspfhVGnWtkHTI/TPfKg6UQUfKCDOuDU8bOHio1jUsEwFWeGgzc4nmJp6dTy6JTNxYOLcW8ZymAccaQqW55vcE/2QORJq4oJxyplqKbQ7kilAxmdqThherHMivsEw+WNWjm1kzh0NDGbYmyp3bV2jL914ty1bP+9yo1Y+b9VDKk5lvQom9JSjki2dRXDeAPSGcbKkGblkj2hIYLyL3nSxMeGVJjnl/7qXf/QRk40PR96Va/m1p1ZkDdi4cfILEPPOFquuuxWF+Z3n4SghoWu81Yq8539hAqhWx8xFkEVFUfZb2O6UP/LHjqs17CIqaGyI/v6COLwluE30/7nGP2wcqXB51UHMwFksSs36C6pGYBTuCIu+xMthRrIrvowSmVSOYpYXXNozX7dhxMZ/zrqLXLZ9tZdPP0g9C5aYwUUp8ayrAdLkZMdDnXPKJjcZg52Mh9QKl3Rx+KY00zdhWJePseLLFzNqaSDfN++y2lgDMBl6r6+PvNqdkAy0JEK8v56QYRp6pnl0kLupuGGsMfWtAw2KF+T7CvjVNZCvivteIxllUp0s4vFsQycxDz37wDoCyNJqyD1qQkMVQ70akLeaow25OgptmoXmUQgCoCaoOIRj4EAP4Xsz+eaNWnuuEc45xEiYmuLKGbLz6JNHoMF8UPIwh58afZIIb31cEPqe0raz7PlegSKilfq2dNWQ16nY8i+PWTbWVAbwnwnluhuQQtexc4dyCKOogUmuVdrfoVLczmCZ/yU0rtbn2EVpnrE8BJdRMXfXrfFqCqobeEAQ8TCwoLoWcNNPnhhJavhlT23Q1gUk1+02jiyDiNe1EEHw+mh0qnaCP1uYHI1UIShTcuS5YY8IYS6v2h1VnTlita+/v9Qfw/2rqWQoVp7ikNa5ow0TaWNtir373fSucW3Uo59T1nAKTbLFsZoQbE8Zn3WxCg2Ej4HFTond5XultzJow0qZN1CSrbhsNNijzROAJB+yPORV4MIXSpbQrAjQt52YrcWAiYatq7zucn/clF2hjhXtcE1kbQogN79xVpwrcCFSlKsFmlUZU5tGGi7VVJ44i8qC2zLzuKjJoft/GmMB65OytjN8lWz3emeZc/cM1+ryJFj017VXjBlqLqQcVabYF36RJS3/OOetbJr9pY3X1SOtWajGHABAcwZiKQxAVgSVYNC1eAG3HBBM4hxpz6VhUMywgn6W9/K9kgYCEthaozdr32cyhHu/9rY0UW52pLoPGz2xwQJpSwEP72ygNZZjIRPNEt5TQsW4h96VwHmKTHyMo32Q25PR3VgLKbM3NfPLZmEY+FW2RCZ+tv+eNrlS30pAENJcgnuPMSiU0NHRBB0aP95o5mXnt/+r20Wd67Tu4FJVFB/P0W5EyOr+GXoVhuqYSFPmbNei1UZhwLkMQUMI4KYWrL73ey+uUZt83wrle1HpxV7FwDgHYE9Kq/GNWX241vC9boiSi6BbhgbZzg2fglNAWOCREs0oyDVq0P7VwZrfPRTeLh1pQkr87j1XgZzOskgoEbw4i6O+0d5kygm2DuCYalEbms0o9Cqz4wJNNv2bx1nvY+h66L/d9QHRVcf5a535V461jTKZ1ikOlF4f8oNlsVrDCDwQT8RERIAQ7CCN1Ai6VV4pvNtGaAjoDq0MCN+GatZ9S3zODsymos29Sm6F+77Siv0cInl3oaElNyWhJLg3iNp9XrdLanW+u9ZqlO8bYup8IMTeCgw5VZa659q2SjnNYLDMQm2a/tioTyPdaZCzilgpVgw6WoU3r+BYRIo01O/XOEt/Ze3129U2op7adAjuPfN/ZrKDnuQTR2Ca60P8RVvAXSAjZmqbEhYUezFE5Wxjr/TIZ+U6FcyvqPlTodQh4Pyci3CI7T809f7vP1doa00Z0LUhQASpQEY0T1OAa5pIf6TGNNQW4SHlLcFctmxZd4axcgMlN9Vv80LrS1ebGZ5CwaX7ZLVisqknuy+xXvyWY6z2536mBtyKch7TbFM6rSg2ug41upQDXCtFJ9as9Dk1TKhAUBWpRbCfyFuWK+AlssE6FdgU0Cc6agdryR6ebMPPbs2lB2CS3QxQvV07Di/oB8QSS2eaqQCdKt5aoWMHzQ4rjfh04e6fCuRUoXQq0P0Ylm7NuVj94NWuBzwIB+XX+GjIFYZUt4svJQon81d3w8RwFJQUs0/Tmyx5q1iVw8b/VSdXbUpsbAQ34SUdoY6LL/5epWiPrrUFiD+XjVlncs03NpSK/rcTAddKr1dsA+eGBggrZIJpK5A90l05U9VlLGmUMtJtMzpy71MEMe58mRknzWZoZmI/Ewq0QrGFK+Q2/JQvlt7kgNWA41O9yzeHfL2D5k5RwzsXcykffFsvp0NiVqbm3SkfW6XVSk8gXBAetjDYTYMFUNSfTnpDwOviyWPgEzuG592lkLoScOUHkM9LUIB/fbUOU/VqrLyf3dCWkPKma6PtKOKeZX0s5Ls2COue7JtN/HcS6VqLOVoynDjS96jPrtVeUV/vIyU6iSRtKcCpm/LBwHhlPd6hn+9r787aGnR5jsa+CPAOLQ4K2lQ07NcjYgtAOzcHcKiY7RFA+Z/bmw5rzDB/0lGK429DgW2XOq8BtzV+a8NTabueU1oRbjXi3cMmJET/Ufcn7SjhXh34Ln7uLzbElnIdGAM7BsZOHueK3p/bNPMRBWHsGzKrX/198y3sunIfG7x3zQS8ZQG2Z6kPJgak5V3b8OUKzas5D1ZuHuAqnuA0PZeH8fywq5yatCk5qAAAAAElFTkSuQmCC', plane: 'image://data:image/jpg;base64,iVBORw0KGgoAAAANSUhEUgAAAJgAAACbCAYAAACeVlKPAAA7YUlEQVR42u3d5Zct31HG8d9fwgsgIcHd3d3dHYKGhBCcAMElECAhOCQES4CQAMFdgwZ3d3dfh/Xptb531d3pM3dm7sxcfdFzdPp071275Kmnaj9wOBweuJ2P//mf/zn0/P/+7/8OXjv+67/+6/Bv//Zvh//8z//cnnvP547//d//PfF//uM//uPae+vvdQ5Hr52v7zu87vM+89j7Hv/7v/97+71/+Zd/2X7Pa9/z2GeOXs9rXq/ntGPVvR471604bjuBapCahHXip+D9+7//++Gf//mftwlcJ8LrJm5OpO8SSs8TTu8RhL//+78//M3f/M3hr/7qrw5/+Zd/uR1/9md/dvjTP/3Tw5/8yZ9cO7z3F3/xF9v3/M8//uM/Hv71X/91O0+CMw/X6eh6ErbuYxWIhPa047W3QO4L2A0EzOSbFBOUQKxaZZ2YBLNHE36SFvD/NNrf/u3fHn7/93//8Eu/9EuHn/zJnzz80A/90OF7v/d7D89+9rMPz3rWsw7PfOYzD894xjO24zu+4zsO3/md37l95js/+IM/ePiJn/iJ7X9/+7d/exNGQueaT7rPhKh7mdc4n/e9qfESWkJ9kva7L2A7Jmk1S+vgp7kM7Pz/BGrVejTcn//5nx9+53d+5/CLv/iLm/AQlK//+q8/fMVXfMXh8z7v8w6PfexjDx/1UR91+OAP/uDD+73f+x3e+73fezve673e6/Cu7/quh3d+53c+vNM7vdN2eP5u7/Zuh/d8z/fcvvP+7//+2/898pGPPHzsx37s4VM+5VO2c37Zl33Z4SlPecrh27/92w8//MM/fE0Aab4Ef88dmAJzTOj6bqZ3HaP7ArYI2PRxTtI2tMI//dM/bRrC6p3/T7C853Nm7g/+4A8Ov/qrv7ppFxrHZD/+8Y8/fMInfMLhgz7ogzYheeu3fuvDG7/xGx9e7/Ve7/Bqr/Zqh1d4hVc4vOzLvuzhZV7mZQ4v9VIvdXjJl3zJw4u/+IsfXuzFXuzwoi/6oteOl3iJl9g+9z3PPfrfV3mVVzm85mu+5uEN3/ANt3MTxg/7sA87fOInfuL221/7tV97+NZv/dZN4H7lV35lu0Ym1yKYrkFj0GI5prHXBXq7mcfbxkTml+ytRq9pLH7OP/zDP2yTkQZbB9N7NMSP/uiPHp74xCcePvqjP/rwLu/yLoe3eIu3OLzBG7zB4bVf+7UPr/RKr3R46Zd+6U0wXuRFXmQTIq8Jls9e9VVf9fDqr/7q2+H5K77iK24HAXr5l3/57dFr33UQKofnPncu53T+KYjO9+Zv/uaHd3iHd9g0o2v7wi/8wsOP/MiPHH7v937vmh+5CtFcQL7j3i20ve/dF7AbaLGEq9U8fQ3HdJQNMmGjAZ7znOdsmuFLvuRLDp/0SZ90eNjDHnZ4u7d7u007vc7rvM4mAAkFITDhjgQrwUloPH+5l3u5a5pp7/A/Hb7r8DyB9Ny5PU8r9huEzbW94zu+42ZmmdYv/dIv3Uz3T/3UT23+oHvLFCY0mcV809vVLN7WTn4CF6RAa3nMuSVof/3Xf735VD//8z9/+JZv+ZbD53zO5xze533eZzNNr/zKr7wJDs3RxDJzXu9pnjRSWqrDa+fqfzzv8Hp+n3AlqM45NaDP/Y/PXAft1jldp/c9d+3u4dM//dMP3/iN37gJ2u/+7u8e/u7v/m6751yIFtz0Q+9pAdtz3ldndVX5E0+aeJXv/fqv//oWyX3+53/+5kvRUCaMOWryTGyT6tFrvtFrvMZrbALgtUeCkSARCCb0tV7rtTZ/rO9532uH1x2953Beh+cJoP/vPAmda/CZ60zgE2LCxr8jhHzCD//wDz980Rd90eEHfuAHtsVEqPZ8sNtdyG559Lj6XOFTDprLe3AnZvBpT3vaFqW97/u+7+Et3/Itt0mdJqoJm8fqOyWACUQaqIMmMvn5Tj3fOwiF76SFpnnNHCaYhCzh60iw06R+2+F1gQJ/7VM/9VMP3/RN33T4mZ/5mS0ibkHOIGAGQgndjeCLqzCxV+rETxxrL0RPsHzusWiQxgIlEKzXf/3X3yYwZ9pEe21SEhpClMA06avwzfenWZwmNO1E89BsHZm/zjWdfAJHSIoqE649X2z+9vQDWxi++8Iv/MKblmY+P/MzP3Mbi9/4jd/YTGeLcGJue5DP3kK+YzXYXjQzEfTAwjWdM80hVP3Xfu3XNqf3Yz7mY7bIyyS1wvNrEoQma/pKCcp06PPNmKHgBkJIkN7ojd7o8PZv//YbvvWBH/iBG7zwiEc8YnPAP/7jP34LHh7zmMdskIMI0Ge+I6Ag+CAJUSIzm79FOBz9TsKUZmtBzIg1QZuBhOt2Ps/f6q3earsGALDF1/hNYPpYZuRWgLKXprFm3m6+nzYLephottccW2DoF3/xFx8+5EM+ZIMYaI0GPZ8q4ZlCl8bwWVGgz7xn4kVuhJU2ICDM7Rd8wRccvvzLv3wzQbTDd3/3d28I/fd///dvKD1nm2lioh2ew9ZgWfyjEH9o/9Of/vTDk5/85M13+uRP/uTDox71qE1YgbUJHyHKvE7NOSPP7iX/z+v+p4AAuAvm8Pt8NItyLmhR6PTPphabudI7VsC6gVVdJ3g0GlDUwBQt/vIv//IGRn7ER3zEJgxMYEKV2ZhwQiYmocuXMVFev+7rvu6Gf8HCCCuQFZTxzd/8zZtw+L0/+qM/2qLSm0m75Pu4l9JOIlwYF6F7whOesP32h37ohx7e/d3f/fCmb/qm1wQn85kJnybV57RcCyYBpBF9boyck1ADlY2hezCurmPPWkyXpPm5TNN56ej89Lu6qXytHFIrEI7FHDFVBpBJyOEtSpsQQT5WTnU+mf8RhdFSH/dxH3d46lOfumkiEy4CFTDwX0xCprtJmLnMlfnQ9TZp66RMrd15CS2t7DfdI/T+x37sx7asAjPHtLov1yxbQEtNE5lfN6NQh/d8H1DsIGjMOLP5h3/4h9s1up6S+B6PLZy9dNwd5eQ3QZM9UEqHGmcOoe4ghzd5kzfZBo+geMxhT6gMNDNT9EioCJdBF3HJCxpoWoq5Y95+8zd/c1vZTDJNOdMwM4NQMvkYkr4e03mepmfvewUwfl+ai4aTVHeNzDNzakGIjLkDLZiiU/dLsyV8M3vQdwnZwx/+8O3e3bffMb6xPLrPjsahBXXHCFird96AG52Rjpu3ovk0VrKBDSLgNxlMpo2Jm+kXGkxEldkwyL4DDQe2Cgqe+9znXjMPx1ZnIf7USusgn9Z07J17TuRJAuu1a6VZJcU/7dM+bQsy3Lt7c+9pLmNSCsr9i6Z9ln+av2mhOQ8B5s8aa7+TNpsCVnCwp5EvTMDW1XZRpjEO1PRRUtV//Md/vJkuGA+tNYHNiWnl8OajGMQHPehBhxd4gRfYJuHRj370xorgcNMKof5po7lyJylwmr9p9tbvHONk7Wmvee9TwDpn7kGpnpgfXcPUbF/3dV+3BSECgwc/+MGHF3qhF7rmj1pszGMLcWJnFptFSMvTiEwxBofzdy+rqzK5aZciYHuDcVZBm7myNEEaq0jF+3AtvpAIES0m09cRzJCTm6ksIvT+277t227R2ZOe9KSNJWGV0gKTXJhGmtjanhDtCckeM+HYZ8c+34Ns9hLWc+y9zmcDP3zf933flp9k9gQFhKsMAoHKhBYM9OizrAG3gwkWzBDgoKKu7Rhp4EIFbFKBzytg07/qHKHwCZhIjXBJ8ViZBmdSXfIlZtTYgFqZBplTzMdgWqcZnBO4pk5WwTrrve35VMe+d6NzT47bqvUTtN4nDMaM+eSj4qJxDzqYx/wxY8SMwvYSsoc85CHbAjXWj3vc4zY+muAmX7TfOuZ3XqgPdiM+0R7PfQ7oTE0EQVgxYTNMF5yIv0V9ZwIbGD7FhBeKkoomYVcwnx//8R/fIrJo0nthd9dZFHWMR3WSZjrpO6fB/fZqA04D66wm3P1YSBgjP/dzP7dpI4CuMXnoQx+6LcjgG9o/zK8UVOMJNxNRw/gIV2A2atNlJ83P5FvtSfk68C7YxceXF8WJliDyUGiDk4NekjeVnhkwQISO849p+jVf8zUbG5XQzsjsNFrj2OdzkeyZyvNmL85CAFyzHfPeZtBhLLkXAphv+IZv2DIJ6Egc/JmOoumjCFm4xjFS5Ju92ZttrNvv+q7v2nw9c8Qk57Pe0ihyaod14KaD6HNC1UXzjwCN0GxRT476RK2LlAhUAue1/+GrFRWmGVPvexM4caw7gSt1Gk3nfmYlFMFg7mQLgLalvyxaQlUw0BiXcw145pfBHOFlBWMFAeddrCcK2ElmsaMQt4uZUUmH1VCk6DP+gyiGM09rTYpLq2yG2fwHA2WlMaXf8z3fsxVQtNICDG+36pmLzO2lvfbuK4JlwkYLGSMkAOC0sWM2jS+gObpSwUBgrdd8WdH3dPyPcfvXqPqsi/eBPXBwHmkOEwwcTTsdq0/0PRgXVFkaww2HYYVQFxHGvcpkytnBcCDvhCtBLvJKc93OVTSXJcQt3jS0cVY2J2eKpAg/a9GWw5ys20wpIRQk0GTmiKCmFOYCPgbxBG+cdg5OJWCBp1NVl7AuqRrmRXMxizRXQkVjueGc+/JuJXF99h7v8R5btIRF0W8Q6Fmyda8J1rFIc6aijA8YAmxjgRKkmeQ35nyw6fcad8EWHPLbvu3btiBijcIT6Omfzrk4LXZ2QwHrZLMsrDKxilV9jxMqwoOmcyZjNcSRKn84nXvvU+8f+ZEfuQmlXF3aMFU883vrTd0JftZlsFOmuTIfFqKFSViMJWiiKLx5KMoMV6zABaArwoe/Ne6Tor6XnThL9fipBCy1mNqc+TUQhO/RXPKKOFLC4pij5RbjXc1cG8dfgluaBLpfKVq/NyO9fu8qKCa325GFmLWggbO9Ng/GkJCJ2KOSsxDGPEEjeBEIWBGOPyGThAdblMqbi3ny+S7cBwtPqtBgr5+C9/Gk3JiLJzyEiRoORA16CIbA85KYlpgVJa6wR/WPM8WRsN8rmmud4MZizskaTRszVCQLFzg9adnGntWYc5EACqzQi4y7+ZyIQYn6k1gZNyVgpTH6kUm3cUEQemgxc1ciusR10YvHillhOJ/7uZ+7Aaf6P2QCJw9/griz0vleE669VgJZk3yktZcHIZPTVGGOC1c0abHTbMEXQUXmiSaTZUGmzAy2mEtxrVDVhfpgRYupao/UMjxFmTy0HT24/GI+Vs5lvhjzSRgh00EbM/Ha7xZATPt/LwrXHh45OWvTP03wWvisCh4/VySqDwgj0iJzWbAFSpKOsvAlyI19AjX9v7MSI24oYBz5iSi3ajxnszmI6DIu1EXOpCzTmNZyUzhLGBDMYoWlwR/T1+JwzvRFmu1OqAO8rKMFPn3QCeGk5ePZra6LsTcH5qg6hcrozFkMDRiZgAtMtBID9tKENyVgrRiPXbQbormoYRl/uJWLZ8dpLVqMxkLDKcfo4q0Odh7GxSwWhU51P1Xw7I6TWbhs7tLtLFwt7gRp4laTqbEeBIUDr2BFJXkMFXNj3mKtMJEEjN8sUAPiEug10MtkntsHW/NocdUnwOo5EyeVoxKH2YvKG9My1N5zwoeTrkABnFFWoKh0Yitr64A5gGfBX+4205grMWsge70myGfUb65YBMrAHNSfg1/MHwun9DxaFDP6GZ/xGVv+N3xzmuS95oDnNpFFjgQtZiohkdmnTqtyIWBWQ6mfysPYf2EwfAzyPEG8PaE+1mXwPGmKuw1o3WtUt5dcz2+dQROrgXSgoIaQ8cFYm/h3KQPvo/oIxIC34KdZ5HvmKHKPjTmbnc1OgjSPymJ4l7KpeEmlfIIjyuI7MCvdmGBgku1OWgEn5UbvZSf/POBsloKgMZcoOx/wAR+wWRvM4FJLzR0hS/AoEFEl4UyTnZtNsYa7E+uaGXcOOlWLslzYO/lI8bo8lx9TsqU0LByn9Eaa7FaVtN9LWm/CS4RM4z390WJeVNSca1ORMk2nbYE5n3N1o+6NR+k6e6ZoMi1pMHxxwlVjkaS/aCQ163O5RXSbzOuakb+Ixrf3j5OFrIVd5M8f4z8rODaPtbCabRUqB4QGcHHw8UoJrjT4M/PBVlufPRc5auwGZgh2mLY7576iA9rL92NQurGghj26z/3jckzkCmt4bS5ElsichCzCwezZEYmRspBbFv3LuEz5OI0/dmJz2sn1Ujn82Z/92Zvzp9gzKa92cVYmIwuq0GYau8GoPJNBeV/ILr9Td9DSmv4xNzhh5spczl5mERZrLiOtB7DVdOWkFvBHq4pWstuqwUR/Gr2puStBmhNfVr5wFy1aYQbHkMSHpWS7i0rXjjv3j4s7Zhqp8a1VQ69pMa079Y6lNGpHwOWpaR83h4Yzv3BNSAAfrvOttPM9Qd9NQ8wiDscv/MIvbKS28lggiZLYpJxJjHuEL06dBvytKaAJGt7LyPxlJ8fXHO7sG5Y/xi+WGFcQUrW4ecwvi9vfIwuWw79Wkh2j8Fx3URPonG3AaS/ktKKNsBPCJqSthxY8TGMRBLZJjFtTHK2w+8Jw+T7YWk44ae0+k+4zZxWR0F6UxgzaSo4jhaLBs0zHWs7v4mDHHDYXwu5CdaG7aazyWPyvOvxRoXpo8dWo38n3XgUsnO2+IFx+imld2NVGzs9F+lJ+3Jtykjn9zW+dfsAWiKGnDdRO5IDzo2gvgBtnr37x0TsmkQ3HW2SS31UHvlVdz7zivYrMX1U/3HVjipqvhGPFVoEQaL8gB5lfXYO82kZ5NP+IDWSifPKNcLijMIXI8bd+67c2UqCkKKdvVqiE3BMw9YvKqAgX7ZUJTB3PLVBmGf99J/9yha3ijBzx/N8WeJ13LHSBHGwMpy8mcjhnQRzl4nPdgFScH8sPT5D3eaS/D/yglJAMfD/gkdZiHss1es5JVN3iouN2t4Jiwp7UH+Kq6xDvFVB37dY9GcrmZG7LY26kkXD644zFdjXH+dweZQEEcvKUK41qBeufp1NMZEIV2VB7P9aJ01wEjXCJLhQY+B5t1//OxieTZjN/47TdBG9UNX2aY3ZcnF3/ZoX4eYV977fmsddYZmWontSA5TJMaPOyZmr421/1VV91DY6qLfyce1aMe6Q7kmqmgPQVmO+9BybgOcuS8LNJc002avoWY1VLIbCF1pRIbXv9Io51O96jfpzU9G2ukAl3JNDzd/bKrXJwadd6wdY3Yy+yOqt2awxn95rImvHmM0dN8Gwluu4KN2sf9nqXXZbvxj8DQ0RkgI3lFpWh4RaRBbLBb5tuzroN4WYi1/DSP6DjCEe1SqqObjbT8AM02Nu8zdts9GeA3Y000rrCpxo9qenInqBWqsU5deRrHGsnsD5fNyadO7adxy+c2mnSl3MPGte9iH1daK5NgNSGX1fpRhgTlgs3H2xRS4Jaa9FctSTAA9Qbtu6RxxbkA+vWcQaGqtSBeTaDy/HLDxNtoH3wvWiEY5tjHhOwk3aRPU2jEBoz4YoEiUrEVCtCkQflJygs8bq9HDPh+YdT6yYYZ53Q+T/5OLM1p9eiLr062lIQwEkD/OzP/uwW9is569rcy55FuGwN5v4Faua0iLJmxea+fZ8qING2QC+zCqT3diC5blWXQnDzclTMYOqxHNXs2wUT8QMTIb5RR5s983dS/645cSubswlgiqw8nWNQUWQdqHDkOnx0r+VG3ZdS+dmr1f/O3Oh58qNTg0bObEw9N0aEna/6WZ/1WVuS2bVppKfI4iu/8is3B9v3Mt1FfFehwea8uRfC7jrbNqc0YNVhBI9scI+CplarEaH0gQY3ZxwK74ZnldDsQVUilArl6OUDnZbpuDqxK/fsRlps+oyxa92k/Kcbdt1glbkZg5WnE42aAGqd1nCfa0vL86auJvu38r5YpH6Lu6FOUQmZoKnrEp3xazjVcEQdDWneOjbObaGvkkNmXCXCzfHcjmd2n9TK1Fh/9Vd/9bX85ByLtPoDsxWS1QPVNRiQ+Sm1mUrS67nVJxBYI5GzCtnUYHta7CSBEyYzgTL9GrPVAio13r6QAELvt6OZWgL/14DupbPOMzmV4WUaf/qnf3rDBwkPoQ9LwkapAiuyAEFzD6yC2gXmft3O77J5c3NvA3NL+882W7NLjwizynzWYxajTPjjOiefNmBGOHDtTJaAxVZN6ISz/JroPOfxF/ac/rX+bm974VmSxVcE/oXbrF3/al1gQuu9byIJGaxvbnFz3mitxZI2d050GFpVoDS38mubwSp7vG7jUu+hxki5VQB7VeZx4mOe65CEaFgf/9knd1bo03K07vTD6/5jTB+YPQ7w5m2pUm+puj+3bUs+mEFgljh3pRzO65Aegy9WjTb9PBdOLVPjUhdx0+r4F307jlpm3iRS7T6T/uJkM0cJxl4T3/M4+zSr8aEt/bbfJGCZmFijXWtVPtGXi9A0k7kVLaJqe0rZyNK0g8rExQLbvZY6sqBWbb45+ZPGIdridLbLV+htmsCg0BYiDN1c8g/22BHn1QRrK/BJgJy9MJg4KQurqc2mopZMCvBske4+yqkCiN0rsPCiuGktClGhsn29IYwjrdo1NEEEqoXs2msKU+8IppKGnnsQXWb2YWJ5+eRMn2CJa1E1eGbSWFs03rNHgej4sGyDfQ0Hy2lWOyftQ1rrKRVbtVaNHDuDx0meEd1FcbtWbTZ9tH4HTqRXqR5kVhW/po2i6txTk+Easc2NSk0iwaTFrNKV1nIzu5mYIONo15EEqsg7DKmNThP4zLrnbTzv3mhomuSqahZmAGUOaCU4pzmv9UOuByGLWYNSDdqYTn7XeB3+Iyqk1ucWLpUzJWRunEpkBtbmtZfRu3RuVjDbcwIDRV8WQpsRZBZnR58c/kx+eTXf41hrHXWs5u8s9zR9GS2UMEET8sL9tGvCPjlXc1N591Rn7cm9uuzocY6BR1Gw8YF35oetW1BbqKJj20BP63MNyc934KRxfJmOuRVwjInssOhR6B3IeZ6WPmfVDqnc1K5ghHPPBFV8ElGurVcaiLosNzizdZGDzzmbr52192rfS4vxR2nXaZ6bjAKO2bQ30zk3wYp6LjpuIV9Vr9nZC4yl0HAYS7nAJO0V+cEiNQ8glhz7FIFzXNucislzQ4X6+QqttCYSbdZNz9L0yxSwmWGIASD6g2nxDXI8Y3fEY8o0tf1xvWFDpys45Uw7Xw12z6q9uvdK9DFERV/tqxQpMy3aQoiGPLsPFox4rhmyRVQ1/FW2KQgVcE/mmq+aP565LyApuCI7gsTw1ITsgfAvjqlJS1XnK8T7MkAmVK2jC5jJ5susDpr4Sn6Om+YHWuX5W3Ov7Ca0qqfyp91bZsnqo8FqVdTAnnXBzPaihIyrASPK1Ui42pZw7tFdm6sWdD5iPdQI2DGo5rIW9Ey2kw1tIqqhTHO1GFyrhYo3KEhs/IrMH6iboFSGne7nhuaZxjZL0GQWKj07vVx2pn/tTRoDk2BUcjW79q1b1GQO22sxreY9tZuc0yLITMNZJjTHfjr5OtOoYShYqiGva2lPgLoN5jtOYRTlChLc43Tyb5SKu1kcbCbcG3dazHXgBRq3xjpKdQEU2TGWVS4VjV5jT3DcDbgBWfcLarNMNA45s7npwVXV+M0WmuVL+QauTY+FyHHddBOZ6UzYfO5/wC3ybaAAg5hWvhknOYaGkF0dAxMpIszZNzlex0ygQVkF3yu9FS0dQi4TsNcT4jIW9N52hr0nsyAbUTfE/MfG2vUqCLHBA43bXG0m0skAeurjSGkDkm9QKO3kcCetGfcqwC87fJ5FpA7XLHmcmaza3LXGXQqikP8jcO7LBPqeaNhubc7Tls6Bg+cNRip04c9aiDIGs4142NfUugUCNfBzbdB/9ybpfFVo/h7I3IIDGuc+uZdMfD66MWXSdbo0nrMOdjsZvIPz7sZCnPNXJrMRNGB1BsRdRVvxmRSfNBCvRbMoI27O9ZYSikte8QINYeK6D2G1iBktiTbM7ziJ13Qa3G6i4HK6/ERjWovKGZHPzVctkDoPWjCce+mX2Q/iKgtGJnTluTnnD7rWBKyIMq0LfXC/ZOk6AXNieScdc3ypPgWF+PksVKLMOU5TTtxVFs7OVlKZIlELUJNmZWKg5sxlpVelNwzKC77gC26PJlxxg1wfjCmhmE1vzzqpa8OYduGw8i1KqR+WwbW1ABL8dk5Df6F1UXme/exnX2spfis2n5ht0j1HKJV7dn3t2lJuOvlg6skQ+ZhKYbsBaR/8pFIC0+FsAwUTyMa2K8TcTP0q8Jm1SrlrMBFyikDJhz3sYVvuzGKI9cHv4pvxuTjOouB2biOowSznRfH3ePXtlY0RoSqe6eC/wosy1bNFEqHn47gHAQIzw1l23Iq27bOGwXP38bSnPW2TgVg1M6L0KMq0eWrMiny4TTPIx0FrOZ6zEUaMVlJqEPgVfmw217jsBiZ7hRJTsP2+a+IQS63AY3RUlJEgcA6pDOrbAnGvbR6xltWd915m1mHm8/LLgJUQcdcgt0eYpKlcI42F0qPvA6jIgulcBR5XrcXm3Ibo81crBqm5cybSwc/l17qHadk2p1m/KIS82Wd15iCtOhAFTVGUMC/kKldYoXMFFSun3ASpLsdncr1umNqmDbrxSeabArv2czgPG2EV1LkVIs1mMXDeUbv5aShP3ktbrX1Xb0UHolmb0C4uYCy+a81RJi0qsJWMhIVdEzCTopKEozwR2lICTkTw0GKE9NIHK/h5VZylvVq/BKXHIkKCZjEYHFpk9t7If2zyErQJvZxnU9K56ufCm+ViMV4JW9VNKxQxy/yuWsAmy7jxNucCKhqXy1E7gRRROB8rx5JMBsjmkHJGcbxiTxQ2VwdHwKg/qn4S/Is0rsoP2wMESyHtTfZa4rbuNznp4isccrNNeud59s45d+aYAu4cxrhruorxPaaJe+16aFtuVHtOhpHOhjgiYMFTLe83AbPaRWJyX1Mak856p3NShfVzMO6EquiTSIyXXeh6p/d3nQVBWgXY/5MshC6siXoyBJSN3boJGPPhzZMErAJbEcKdJmB7lOy1mvu+cB3fnzINa+4RTROwHPwwMQcZEgVTWtf4YOyrN4XQczfaSZUWIcg1wcum33OnbBC616p9MmavukfGndLXYppJcw/Komwid86mwQSMDCVgjekDwMYpYNF7p4C1mYKawr1d0O7E3qWzM8x9ATtZwAJbwT2UzRSwSKl7ArYRDqeJTMBSfVPAnFxh6Iqs36m+xd5+1PeFbF/AHJRLnXemiZw76coE8eevE7CYCUWRCVj/nImkHv3IHth5Jzuxe9vn3PfJrufnew5LZMVqAD2LcEP3ZVHIUrvnbUg+mEKvhFDa/nkKGLsrggAOTojibpiEGQTcqI3BvejoTyefH04WpowkYGSFDJGlOiduAgb0g3rrlBO3fRUwkYOUi5xlCdA7xTzeSEhu1D/sXhewcEIwBSShbRszkVVKlU4kS+0xugkYZBlKG5IfQzFOWGkASL7E7URp166It3MEeVrnf9Vge+bzbva75jx2r2QEQQBLd/aJmxoMKI9PCGittmETsHKRNgydxRKRDf0z9FauUkpJULA2HLsTHf7TOP/HuhLerUf3v2ZOOO3mXuvMajSi1ZePrHxNOrEMxQZTeFGyu70eYyzOQlECKHmMXr2mZC6y8PZ2ELJjgOy9sIHDuquwR1CWuScDUzamH5YSes5znnNd8e4mtUwfrlTMz5Le01Ry4GAc1elNPOxu2ol2zyzeK2ZyVs9PATPn5p6fHslwUuq9V76aKb2OD+YJSks9CKLnTFPJ0UfYU7GMDJfjd6NdHu6mnNy9EATMxTXvXaMZXDqEw2CsSgVLFcFKyZBA8Loerf4IQTXbALai8OaLzdo3kaSC0iixs23k3eyjrAK21479qnpH3AqgtTQRujwMrJK/LFzIg35ydgsBZV2nwfwBoKLrUoGao0U8jPNTXweMTISyvUYhd6uAHctjrtrsbhOwWfRhznXQqVfY3D67QhBUHYU0syH0tQZ0VKC2mZw4BRO0Vb0UZoMOpH5A2myTeLcJ2I3oO63MdQ+Am+krdjvCORXYeA7bUqdZHWSddWpDVbMWFk5V0XVOvoHixGmgiydOg60bhefYiRJs8B5HaC9yvNPN5erk36goYgrZnZzdWOctV8DzZz3rWRsdmkzMxn4O1o5SwnbF28ckrs5hgynCObBaIbV1qJmga48iSZ1jKmy4W/d7nGbxRs7/NJV3U4ppNmfWOoAJLLE9W04xl2RGKpEMkaWJjT5QHZ9CiZq+1stq9oFyMklvJVjxyO/lpPDseH035jFnZZPmJ+Y+WZjwVQpI40IyNLuObz5YRRDqHfVTmG0oO2HhKJXI2eOzVdFzn+ZyfaS5l2q608ZnNjUGS6n6r6PO7L6UcHH+9fmofdNEF66pQ7QdTcRQLmYbylRiFUYajshdVtZ+t2Jg56UYz+O0u5jcjovF9TJ35lrtZv3hwkUrbPY+qhfLhh29uk3XpXxU70Jj+8fpf7XDmkDAFryKMY+F6XezSTwmKMdgjDtljGata5kZ9Zq6LiE68LNq2TQ3KfVIJgCxe92JrjNxiivZ0slWjD7t0F+Bs0dlKh6dfbHuBjN5oy0BT9p2b8XKqhq/2R78V4l7TfzLAdPSW4NVgy7UzG82NSYXfHfw1QrlbDDF7JKjaFLpfV2Q50YMbeEHI5MSgO7Wk/N2Tp3caC/Jwyn2fDxNbnLdm7J6zTtFwGYFUS2yZHjgX+Zc85jZM65sD4IE3x3bYjIykqvrVDuQ7OlPf/pG3i/nVOvJ2XtLtxjaDuZR0/2rSnZPv2aPanKaLoB7u8Cd9zjcYMOvtVh4/s+6t0BtEWY/ij0g9zJM49oOggskwd1+RTNyjFHhuaYnsFHZoBlRd93XmUhOGk41QHXuRrFCFpLidi8r79QePXuTd5lMy7XPRI8ou4TfIGkfUAsBB7rRWQ5UldMc83/6LUfX0KP3RGa+t5IFAm4njnRV/lvCkUXCYLVznbnODy+rU/tP1k1XTCTDSeOaOOl1exV5U/cZDV2duM58nbRNSWv6qkla+9vMtNGtcLp77kZl9PGX7Abi5j126NDo6H2PN3NIo6yH3+4wRr7nsd9XecMdEaVNbZXP1kRfJQyUgDeXrt2eSeWlK/JI6fDHaS8mVMX/bETTua45+bNaG8al2Rh2ohRAZeHtmhFn3+faJZnQq25GN9M1+ThwPGxKOVVhtdQGjpuoWBrDStNH1CPqr0ea2uNJh/856RBhzcNvzcNved+5+ty1qXHg76JA6fmxtmnK0b7KmgXjqSKIRja3xo5iqahj7pqi2R+K9BOe8IRNZuaufbNm43maczAvdZxuhzAn5IsRtHqcIifa6JOZXDfOvOwVN4WrVuqYlLL5Js91CkhCnetn5V7aCKHXPT921Cju2NE5j53Lguw84UcljE2YhiLcDe7JbN00c4FXJWBhX8yjuaWh6pTtuicI7z2pRX7abHayptmua/bayvEDuD00lRORYlygOgrX1twPzC2VZ1unq6rOJly0qAZv8BiT1n4/9WottA6JTt1fxNGOIceOHOTJABV5tYkXV0QLUDw74LXIPEf/qqLO+Tu0l0JsucUaEFo85rwu3mFij3nMYzZZmd2N1mu+rmVRE8cR1eUYfaeKkXYDi/BvVeKPwUk0UZu06cve+WPlzXOa5cvaYq52QuvEFmbP40YCtPc/8yiVduyYzOC5JXXN/eBLulFLFBv3nOwc/qvwwZo3PiBB18NW9EiQom052pnEdZMNJESBy9ztZaX8PA+Km/kRTQLQSg+0XUvbsFh9hI5P0YaUa/O2i9Bke3t4T/zJbwAEgb8myzXWf75mLnubODVopxGQk44pbFOYZ96unrcRCdr0qj0isVQ0/hVpzoqtHP6r6r9GgwpImG0aljtUmrBe/y3aRz/60Ru4GqC8twi8v1vf6DXfCoEMDztfrHwUwWqXCr6YoMD399oKnBaPOm+BQikNIbUBqIRKDQFBM4lzx7N5HHv/LEfBTxy69agJcbt7eDRm2AltwsCZFl3WY759ky5jB7vDka37HBYqf7AGJ7lHcz8l7+PfsxjBVHvcuRbI0cJL6lqoKvIpDxkBkaoMeCXR0ksIiyKQwMPTbPJ53gEsDG47G7+L7CZqNNkGhg/m+sqr1pe+Y++9yzoKCMrduT5RmDHFZdcXH1CZUM0OhzebAdj7/xUI9lt+E3yCzND8ZiLrF9drETE4hu97rNLq2m5rx9o6mjzddEQT5aKalOl7GDS+mEb97Hd760zO/kX7EFPASskI9WlS0AMhm/3oO/Y0z81qsBv5bKHeLc58mFp/c/CZx/b4aezzwdq17LLYq8ZSYEHA+V40/+oz5uhbGAqDBIC+37Xt1SQkSw9MJHl2RPYodJYl13a7lj1tTBn41sWw20JW5moCbTPxeVG06hlJ9h4hg96LJuXGamHeYeOsqziMwzxE2tqPGkOPXQuA0qbxANe2R5ydncOkLipVtGqamSKkiQi5a2tz+mCUqvtTLu7BGLvm2cRv4l+TqnRd6mWqzjo2Q2mRycAUbc/SD7YqSTZfjapXxBuqu6Yf5kXcrOM6r3VGXgBXVTDMu0CFI+qY6HpHn13UsfcbzE6fwRddE2hHctjYtqPt5JFF2svHnPSfs4xb5YUz2T6FIO0PalC2aA5pqtkaoJRQ+z3RXixV5nzSxdfGfteA1lWrzByZE+F/6UsQyBaaO9MHpF00ZGtdyO7cuGrSeqaEX8SqnEHF3H75Tun607WGe83u17NdaXspJWSnqRmYW/5MAHfWUwgsaKT2eypKjO9VJE24IPdkIfek6+4o+zAXwu62eWtCuc2Q2qKlHxQdFWVEShS+MpV+aAUN543f7CYOJ21WMOGW27Hf1oyCDztbI86++muZ3KoxjjE69vbyTMDaQofwMY3gqKrI2ic0HDFg1edkQK66TS8mi3cK2vzd59nkYGUs1PyCmgcItv3c5IzNHem1UZRjEyD4v2NbLnezN+uLTady4nC3C/fq2HWsOcA94HOPTrRXZHIsSpyaa6UJ8Vdx+rg/6FnheuWaC4T4ZObY3JMBPvbaHn6PIn6tCfBpCk/5VEBAuT6MViF2hLPSBplPq0AYq9TJTRSuTucy3+AinNd7rdf9DMaOFf5OmGhiknOhEy4liFGzgKrhdJ7n/rRVn7mfLVSn63NSNdWp9mnMbot4bExZApdAwZvmVsWlFGBSEP4SoXMf6LZQuSzG6r1SYHIS53+6CNN8OepqiREjeAtyasvn9hinNARwIl6BU7y/BGsK8TGf+kx7OgtN0ThoMcIUTuIiXVxRZU6/fhdYDglYEk7AVjbnfQE7f9efvah8IgHtsZ6w8aPQbHLk859zeVIWBE3gxrFPUUytdZqK9lNztbtgkizBLcVBuj3OapO2eXOhog6qlaks477yz66i4udurz5f231O/yhN01jDvMyJuVlzpmktglbemZLQoJCgTswrJsuNIKcz7zhLWGA4TGDodXtQxxeLnOZ93xMGw6cyt5MadL83/cVtFJa/O01Yc0dAVIKJGtGaAs5D7EtpZZloNEQGJE7+92w0eBbG7Zn2D3Sww3Aum2hia5YEn+yAifYzn9BsDTRgLis16L6AXVyUugpYwsC8WeCKM+x30M615Won9ai9w9FxFGInXLMhyrqF9EnHDW+gSGWejIOO1qGNABMZPyxMjIAVldQC6lGPetSWkG6f7Kvepu5eMZUTOsiM1QJz0q/M2UMe8pBrNRYhAQRNAt7c8p8plKxXgnsMXjmXgO1RedJktlhGraalMovZcKsg3wx9WaoBA1JSOp/svva6GO21B6qmzYy1FqkYL5LrIKbSQBECpuUhXHZVk+LCDzPPjuncn+Uaz2zn+wE/qI5SuwEJUAJEkNJY5S27cM81KZPLko9r36OVl7RSuO/2BitnCU7WrMW6DfRsCmgMmTeVTLSRWtbJ+JCFmb2+aLOKqhEccMP8loR7zvx5QOxTE/v2UGaSLSp56lOfukUlz/d8z3eNlDgblDGjbP2DH/zgTdBoMhRhjudkcsyq4lXI7tRONRcJrq50mOl4l1YydqXoCBfcklYCI9FgqFUIg6yLuQn3ev7nf/6tYObJT37yJpgJ1VofcNZ5OLMGW1uWw7R0YHnc4x63YSaEKT9shr/BF1aJ76mrBNy6mfy8OZDta70Wc94JieyLPmI9zGLj8omz4DmNJp0j+pOyk1WZqT2WhvaiuTzn3hA4qSB8ML71rNRf+Wh75vimBWwebjRMJHUpQpGnevzjH78JT/s4V6QZ8h/xzmqyrw0hY+v9f4BgmsujldgNNchXUcp1OzYmqcB5aqy2bMmaECxuC1qQscU7o71oKwufYFnghIr2Qi70nojxSU960kYjEunPKqE9ATtL9H8mDKwcYk7fRJGRE7EuEOuqBo5DRNjipz/0oQ+9LhAwEHAyNl+0sxdhZjqnUN9rzvxEzidnj5Z3qO7h1/JvaS6CZPwng5eJJFQEjMCpCXDU881Cn9qpuZ6L+sI12LT3Te7EWnL6OYNuUqWybtTUbpFk1OSa2FVQkF+gBg+PDAFv0lNmx5cpdCdxoe7GY5awrVu+JAgiRQHXwx/+8E0j0VwtanORXxy/Kx+McD3zmc+8ts92GjKLseeDnWWRnwvQK1pZk6wuRsYdqFrbH459QhZZsedWUclxqLHKoOc+97kbVtbKbICnCb0XNqia+cbpHvSe11wIWr+WCawHjYQ3j0BYEjuTaKzVVhAwAogizUUBnGcKpzmcW06f9z7OzWea2mRWwFRfJ0okNIGuFe9iX1hZVlVFGVWwKC5RBCH6YXK7SYNJQzovobuKAt/bqe9rmsW9l7T2mTESKNFC2ljCtYwx4WEZcujTVgTLgid0SuVUcEsfrQhB83kRhM1zsTHXFbZ+38rSvIw/8NjHPvbaXuCljkL4Z6PhsDNpDCtLfR61n2nID5sa7G7bwmW1ErN900q/oenVrXIvqpcgRDnxTGL1l9gv1U4QNnNCc/HZVn/6ogt9z9wY9pjQzWKOSqFENVZJm4nPNgTVJFZbGU233d5oP9AHTpkiAwMxizxmvu008Mrt2G1xBUqnaZrmsO8bU0KByyUXLEoMzK4Cm3AZa8JFk7EK0dthYIIqGZjKzlYq9kVjjecWsGPpiTX6A8TCVqhxNy5VUTMNZrKd3ayuos2CAt+3QoF/hKyc6KRHr5tn3s77Bp10LXt1BUETjbUx0A8CG6I+HASHOYzLNQFVh88f9KAHbSZU1Rc4iVmcu9LOBbtHv74Zvt1NCdhqIueKTNOITmoJpV6xLeGiWjcwtToycDmkZQUgzFJM4Azl6iVgTwJd/f6xngm3q8DtbWlsfEXXonMpH5o9gsFsT1Uu2GFhgiOMrUdOP+hC6Zz54M/ShgVqE2O7aK7dufNle70O1nB6HsylG1RkQGAMAoffIBmIzGOqvsLPtJrCBCYBE1MAUVFJDUKOtZu8Hc3kjeguPgP58EFpfwW6inhx40vtxOeae0rVzKXxI1gQervkBaKu+xDNUrM9d+Nm2cKXuqn4zOoXWnP+OacceeayiuH4Y63EWhzFE/edQmw8NI3/RVAiqcDA6btUS3hRnLOLYs2uwpUvNq/dPfE9n/jEJ269QZg5kbgx4sTTYJWT5cMGXEed4nL4XxR3AOpsTTAX4l4H7GOdti/NRN4s23JqNcKAE66ihV/GZJazTIsVcc4K48qqrEyDLNVEowkEAIyyCPKak+s/WyDtCchpB2yvVvQsK3yvHnT2AOMPwbPs9aOJDJoyhgoHvd4Ws8g5QapkMFNp3LwnalSfalyKxPu9lUhwUkR+2s7at0zAZkOVqX75ZJrWwbv09YI8V29ZW4IKP2PMhj6XDai1J2ARwCiqesYznrG1QXJuJkYifubv1j2E9ur4Tipk3eskc1LP/LVUv7EgULSUBUGoXDMfi2AJaqpTdJ+zeV5wTwKWaeRqBJ5aePxVtHb+6uzbNjn6V7UF45WkOfb6KmTGRDRWmvo8A1YZHDNAU9UmKnpvfkcNaQkagNH3OLSEzUQJxWk1vt80DWtbo719uGft4dpNcRWmdbvl/JljkI7P+ELYovjxqqVpK/CCe2EKEyzuQf4Uoaollc+MkWhxmk/+VlyulRy4wjvHNqG44wRsNuxdOd35Z8JvAmHloZfUh70NuUL8q1zKbM4yuZp2EEppEuYT/iaowFeDx/HZ4D+0R2H6Xp3h9En2BGtF2ddK+O7Lb2CUigJpFOCmgmRVWTphEyzaW8BDcGqwvBZjzNKyxsaiMj5eGzOLiiOPTSFCnP06Gvu99N5ll/1daeS0t0Ns1B/PmQsBACc+kmLb2VjN+Wj5YnPb56KoukfXzZm5cb5HPOIRWwcZ+U7FD8yz32NOCZ18HLPa5guE0GGy+I3lQuOpMT1SV/6HEPl/zjSNbMHwfZR7WTjuCUTzyEc+couga6icPxUBoCh69pZt5zuPtFX0dAcc0ULSF01Xowqa24qvHGZ1kSftULzX+OYsxR23VMAOR7Yjns6mwRHpmGDthNTuqTwmOLEv1iqYqeWKPKNoF0mhB9UC1KQSXKBjveol5TXZE5XaRoeWAQ0wYSZNQEJYbO7gIJTeUx+K4kIzSYn5X8LLpxS8KNdz/aACWjXhdy2ZwcxfCyinvai6NFqBT9kP92nRCHBcSz1ACEKaeXbjObZX0jH4aa/ZynnhnlvOFMgJnXk2g2Qirf58FP5VIXhRZo3SZkfBwNu5a+9awRw/ikYgAEiShEFYD2/ye4pZlHgxZQRGRQ5h9KhCymeKI/h8Esd8SLx3WFW+UWa9KDlNVcRcL4iudTYfTrtZJO0bFRbI7NPCTC8tmiDMCrBjexacJuKdvcNmSu48aaQr0VjHIrC10ns6wrV/UoUkCMCyMIn1Umg1t0nAbBeeCQ1DW7cmDP3OcaZRaJa0i0fnLYINo5tmreCi7+5twBA9KS01BTuTX8Aysb96u1YAS2A58Hh29m+kUdsQ9tiOaROa2QN5T+otNtNHa8uos5rMK99ueO/GaCx+ThTpVHv4GS3Hr+HEQrWR6mBEwRj1PK3Veu3MTRrzFLyRn5bA5M/l88xW5GmUY73z537Vsz16PtMUtIljpWEz8X2ncxF4FT7+h8aiIVHRZUFsWcz/iwvWdooRQPO/brQj7wr0ntSidG+T1bO0fLhSc3iM8rOCslOLFVK3xRzoQREpx1byVudFExEFKK0Wwp0wxKhNECtAnQ1vp4O9NvPd64G/bnM3hXPdOL1rmEWu8eDq3hz0oLxPHSMSoeQ0d0EgMblwswpr3R/omNk7htqfZC7XPTDP2nbrtudHFf1ME+s9URvziTeWoMkKAF5NksmsM3Jod36YCa5/fZOeRpkN2Kam2hPAqc2m4M6++dNxL+oNiigqFA3yBd0Df8/iAanUN3/vuEgg/DRmb9WAx1yeO07A5uqcKzCGJ18EsAh2wOsXFHC+mVATzVzxq5ie4IuwtApQ27AhQZkdZ6b5mzt/rKY0wXWuzHLNYJhsh2sIFC7AcK2iWNcueuUKFBXmIqz420Vytk57rmMtUC+su86tpA6vPRfmimtl8T/gUOAFKSM7UQA0OcYgA2YHP4qGS7PURbnoLsd8OvUl4+fRnk0J6mzzPbWl14SNZgX+2v6PT8X8qUHE7VK/EABMsGbJ2Nqack133Q5VTjfi7d/2Arb2Yp9N1VbgMM1G2ICkQFB4FR4Zf8akSgLDkAgbU+qAjfF/ZtSZllp3BJkCWDQ7nXim1fnAFardQRh+E2b1lKc8ZUsPwdcAsu2uNnvLrum0tUXl7VLdnkXZa6E5jzuqwmZSW27kh0xGaFsb82mAuKpwgKPgDwArwWOmaDuIPyysDUn5RUBZOJnD8zYyhZtpTQUX4wcyz6JcfiGhlp7yWwBaAkXgCVWlYKepL1gn7nbtslgQMRWC465pELK3zd/UerNQFavTZPPdNMMVpTGt/DhQCLPFzDoICqaDJDK03qP3AJ2+h15DkMAIkH3CxNwR5ra6WzdUmP04uq7L3GPzqnrGrvnmO0LATsuxChic6HMb1mdST2o9cN5k76xbPLavUMLv89mjvgk5lsa5U4RuzsFqMu/I1XKWBPtKS5mCMdX6qvVmldQe42AvqjuJ1LiyNvZ2Bz6W6biTioRXC3JPdP5bMwnrZ+s+O6ct39o7/542miZk7Z96N431upiu7Xh7NwtYpjGTtFdqt+5acVooYCLkx/hue1Tpq9jF9nYpbrnrBWw1hXsabG+3udOCj6tgrg31VibCvdLTv7H8f9iQYyu1VQV3AAAAAElFTkSuQmCC', rocket: 'image://data:image/jpg;base64,iVBORw0KGgoAAAANSUhEUgAAAJsAAACfCAYAAADu8KuaAABBBklEQVR42u2d9ZctV9GG798SEj7c3d0JLoHgGtwhuGtwDe4WILgFgru7u7s7rP7W02s9Z7237u4+1ueMZH7oNTNnZs7p3rt2yVtvVR3quu7Q1Nf//ve/juu///1v95///Gd28bO/W+d9l/l/PrO+xzLvy/97Df1v/Tn/Nv9/3n2yRv/617+6f/7zn/3F96uu1W68Dm1a2KrAca27gCnIY7/797//PRPyMYGo/8PFZv/jH//oN9yL11N46kHK13yfljAOrVfrHn2G/SB0G3vj1BYumtdUi5fColZQIFJj+Lp/9/e//72/vJexQ5DPscw9+9wIbL2f1GJc/M3f/va3/p4Q8hTeIY16IGwjwuZpTy3ROvmrmlAFqQpb3Xw2k43l4nt+x//x/V//+tfuD3/4Q/frX/+6+/nPf9795Cc/6b/+7Gc/637605/2P/OVn3md6xe/+EX3q1/9qvvd737X/elPf5q975BWdS38PATNi9daWvhA2JY84VXgNFOLnNwUpKoZW+Ynf8dnuem5+fyO90I4/vjHP3a//OUvu+9973vdl7/85e4Tn/hEd/rpp3fvec97ure+9a3dm9/85u5Nb3pTf5166qndW97ylu5tb3tb9/a3v73/u49+9KPd5z73ue7rX/969/3vf78XwN///vfdX/7yl16gFL56ELgHNdmQH5dmfK+b060IW9VwKWxuwJjGGvIB839939bG8Rpa58c//nH3la98pfvYxz7WC8srX/nK7ulPf3p30kkndY95zGO6Bz3oQd297nWv7oQTTuhufetbdze/+c27G9/4xt2NbnSj7oY3vGF/8fNNb3rT7mY3u1n/e67b3va23V3vetfufve7X/eQhzyke+xjH9s95SlP6Z71rGd1r371q3vh/NCHPtR/NveAIKoBuecULoOD1IxT+br7XtjGotTqx6WPMuQ0V8Hze30fNgrf5ze/+U33gx/8oPvGN77RffrTn+7e+c53di9/+cu7pz3tad1DH/rQ7i53uUt3i1vcorvGNa7RXeUqV+kuf/nLd5e61KW6i170ot0FLnCB7rznPW937nOfuzvXuc7VnfOc5+wvvue185znPLPr/Oc/f3fBC16wu8hFLtJd4hKX6C596Uv373XlK1+5u9rVrtYL4x3veMdekBHsV7ziFb22/MhHPtJ96Utf6r773e/2ZttgREFbJMpe5O/OsMLW8kHSj9OXq2bShW0FAPVis/Cr0CRs7IMf/OB+s6997Wt3l7vc5bqLXexi3fnOd76ZECEoCBdCo+Bc+MIX7oWOv0UAvRAkrkte8pLdxS9+8f5vEDL+nv/jutCFLtT/7KXAIpj8DoFECG9zm9v0Asg9cq/4gwhcy31o+X6sQ/37PS9sm1bdaRrRSPg4mkIFrxU1crHY+Fps1Oc///nulFNO6Z7xjGd0j3vc43pziNlDwyAoCIWXAoYwIHgIGT9XgVFbIVgInsLlpUDm63zvxc+8F5cCzVd+d5nLXKa74hWv2B133HHdPe5xj+6BD3xg96QnPak3uWhiNB6m1vVRuNSAywZYZ0jN1rrSBPK9wsdip38nZMH3v/3tb7tvf/vb3Qc/+MHuNa95Tff4xz++u8Md7tBd9apX7TfTTUarcCFUbH4KTn5NoVErpWC1rhQsL9+Lz+FCEyJYfEVwuSdMNPd0jnOcozv72c/ev8b/oPEw7094whN6f5LA4zvf+U4f/RLtEil7GDP4WQf0PsMJmyayBhEKVjr6+GL4Ye9617u65z73ud197nOf7prXvGZvpthAtYeaig32YkPZWP4G4eNSQPLvvDCXClYKn8Lk33j5GSmwfAb3kubVg8Dl5/s7fua9rnWta/XmH21H1PvDH/5wthasEZEuWj0DjAPNtqKWSz8ODcfCfupTn+p9nEc96lH9RlzvetfrrnCFK/SbhLbIzdOnSg2WG8yGYl4VLP9eYeT9EGC/qiH1vxSi/D7NbwpxNcPp06VJ9/M9JDwbvubtbne7/pnRdsAyaDqEjcsgwYO6TRdoR4RtKtVtVKmfgmbDdHzta1/roQogChb+Sle6Ui8ERx99dO/k8z2biQApYApTNYf8zs3nZwTFaDK1lUFBaq568bcZQBg46KsZbFQh5PJ1TStXak2+J7jg4m95ZiLbhz/84d3rX//6PpIFTE4z6trtxN5tRdgqdLHsgyWMkf//5z//uQdZcZgf+chH9iecDUGTsPj4QESXbIyRpJvFV7QFgogQ8Df8j+ZTbaXG4m95P2AQHHYixTvf+c7d3e9+9+7+979/d+KJJ/ZRLRgaF848mBomHOeev+V/+F9M+mUve9nZvfoZ+GfcD5/PvShUCroCrq+HQKox1YLcNz+zFuCCrA0gMhhiK+gaA9mTKLDrhS1R/WR0LML+yL9PIJOTqZCB3j/vec/r7n3ve3fXv/71+8XWJ2Mz1GKaITVTai8304iTn9EQN7jBDbrb3/72/XsDwD75yU/u/T9MNFkC/MH3v//9PSSBk/7xj3+8++QnP9lHiZhyTBmvf/jDH+4v/vYd73hH94Y3vKHH8ngvfC1MH58BSIwgXv3qV+8PCNqM5+G+FXa1qoeC++Y5wOw4CLyuWUcor3vd63a3utWtevCYz2bNMKsJeFemTeZjM6rflsZb+R/N780TxqG8qL8zZYTJRNC++c1v9maCTSI6UytV55oNQVu4UWwIgsZmsElsKhfwAgKGNkD7oKWARxAqMgkAv0AnAKtoCBP0Q/nVIRqS90/USM6UzSd99d73vrf/rOc///ndox/96F4THn/88b0WRQNy72ph/U7NrtpObC+jXv72//7v//rf3+1ud+szFV/84hf7ACqT+clU4Xsj+jH60hirZuvCNpb0rrk/Hyixs8wJmoxmg973vvf16D7pIU42px5owFOu35X+kI412ussZzlLd9aznrX/PVoEHwezd/LJJ/cQCQKAn8OGCCWgDYRY6r3X1JgwTP5tzWDwXrwngsdFaorcK5+JyUMg0IQveclLelOICeYgIHDcO0KHiUXA1Nyaf/6GrwLE/I1rw/NyQF/3utf1kJAQST6TwUQr9eWz5us865Tabe0Ee/7cAhrzdGTy3d+xGSSxX/ayl/X5RU68fphAqJFdwhBcQg1+f+yxx/ZYG/4Vpoy0EKYPqIRo1qS4KaGkHw1x3lpcterzVGFMtyDJBryG9uRevvWtb/X3xj2i9fBLwdgwj2grhAjtpS+qiyDorLugG8H3YIwEUKTkMP2srUImfSnvORWCz5B7N7U/N5mKzER4vUEfhIfnod080kr4QCD+ONZoMU8wQgQYivngZ36nv+KpZ9H5mSwBWgxNgd/EewIPKOBD1xBGVTlsY+ZmXn4X7Ym2qxw1Nxzth1YnSU/EzVqQs+WZ9Du9MvpNaKfCKLgfCC9+rzCJoLhYnQLWOlibgk8mpRG1TK0+gieFhReYZXHxYXCCCfFZLPwrhEk8jEXFtwFz4u94zYwAPtk973nPnl3BwgKRmNTOFFfmVf3ZhH0rKl7EOa7J/2SgVNJomlzBat0IX0Po0HikqQhAXvjCF/bPxrNjNjGxPLNClvlbCQB8NQJGy/P/+L9f/epXe1POvaDdff7qk9U12HXQR0vQqnlKZxSf6TOf+UzvR+GvsHiJ5usg83PiVkZonOrrXOc6PexAtEr4DwcNIWNBM+MwBsl4X4vWGtT/rSTMIfJAa70MlIaS65hasyQcpPve9759BM2BM6AQ+E2MEMFjnYSHOIxEws985jN7s4qgeV98P6S9PKS7VtgyEFBdVz+HBUbQWEAE5phjjunOdraz9cKlYLFYfI+woe1cWBYU00JECawAaREByw3VJxzKF+aijlGY5kVoaic2zMhuSLNrroc2rx7WipEhzGgmNB0cO9YIzY5Lodk0ejVw8nUhHwIu8q3QmrAqQ+5PFbZdA30MnQKdYBYpTyy5PViuqHZOqAKk+hdHYxHzNRYMbQZhkQwC2BcERLWY/khdsFZByyJVTmMCkYUwaT7H6hfm8dF0LSpdSLIBF74u/i1QjeaVg8dBrawTf2Z90XBnOtOZ+p9hwABQwzpmL1wvNXS1CJuo7Jokl1lTJgiCwsbDADnwkJg+Eswi/iwCOFiaTiMuaTgsEmj9q171qj5FY5ChX8bnuCiV3dqqglpGm7U0WtJ8hqq7Fi2SsSDG9+Fr+ptqTqNEDhbmFXgDvPAmN7nJYRCJmQkjdHO8Zi3weTHJ/D9sEt6P/RH+8YAaVe8KnG2IxKdJE+ORb4bvwUNiHjltaCoECZPAz+YHZWWo0UDIYbeCkRnGCyFkcUg15UO+5DzK+VDZnS5AKxCYkjY/BBhXv5M1JXPBASQKZ/0QKgUL4cs1Zl0FjQk4yJ5gZQCz3S8Pj/tWU2C7xowm9SUXDtX/2te+9jDTycJwwhQwnFiT1KZviEjJPxKtklHAz6jR5TzGbi31GwsAhjY68adFWMLbYDdLGgWUBtYgCic5D8bm4TXrwuHOJL8EAoSPGgpMMgEb7ycGyXOi6TjcU9POJ2HaZtpKqANBg4cFUImpNKEsZqR/oUbjFPI9poF8Jb4ZQpbaJUHHeYn/1Fa10ryCl2OabacFbV7KjDVCy0EepRhHsqbWQU3H4dZ1EU4CDUAZ4MOBB/p8rBFQzFg6cscyCGodb5QTBySBjybNR/5+ApCodRZBwcOfI5FNuiWLdluaLAHJljZKsyemxntmBNkiB4y1X9gtvLB8RgMkNBH5UQ4362lxDhdWBaBXfM5Dzn4goGBxmtRcu11hRhPQ1IfyoVHv5P4wnTqqOvw6sZwq4Y0zn/nM/d/h0+HbkRjnlFWBrmmUlrAl3JCClYJmLWcK85DG203XkMBzv/pcAMKnnXZanyPFFamwSOKWYnT8jA9H5gUloUu0a6AP/TQ3zcXAcYV6QzIdX4wUE18Fa01DSbfmdU4dgoYmBDdLDCt9hlbieOzeECqcXO/RKNL39lIQh/Cy3aDFxn6u7BvcF8oWEThSgJhUfWEpV2g74SVxTPYAJcEepqVatf3ERoRNgeCB8bPMcxqC66vxcGo0oyZSKmA/4EdGmwKZCB4CI96zCCiboDI+BxCMrBIXUI2cGm8vCVs17T5fJtn5ypqCS2ZqS9CctUcICSqomYWqhDJA4CBFqN1Yv6k6UB0hbIu8We2ZwY1g9kgZ4aRSFyDzVfYCJ4iHQ/gkMyJooNqf/exne0HTlKmBxHtalKUanVUohvtCq4n3JUySNaj6cuJ2u1HY5gHEBi8CwQodYDAZAwicBF2sPRrNvdDKZK4V4YMxgnXyfSrJYDJhG3ozc4hGZwKRahGiGRijsFERJh/CgEB0G43Gg8Lfgkhovk7e1FBUuMyGWCCjZhO4bOUtM78pp22vtjio7bVM7qPhnvjEJ/bpQaEPc81caDRcGQmpUJye/exn974zB7biby0feiOaLTfDIIHQ+41vfGOv0XREMZc8ED4bjioPCGvhqKOO6kl+UIGg1SBopp2mAki5J9/X5i5qtso9Sz+uxV7da4Kn/5bgsyYVDYd7IzNEYZMnyJ6hKGA/kxokYCBClQunwlm0PcTSPltGg5W94aaCpeF3CdQKzqavoL+Af4DpJBmvo67pGuNULVM80xI2fbbE2hQyo9RqbveKsLU6I9VuTygEBE4WtBVkkh4UOgtzcH+IUN/97nf3eeikiY2RClYWtmrSspker6NiCbUf9rCH9UKEgFnehm+g6dRvIyrlYUG8pWTXDR3rRDSWxkkT6UnMaFSIowYG/I6/4VIoN0Gt2bQ2Sz83hdDDI4mTtae/CNYmi6PNLih0+tm4OkSoCW8ly3oSYaskutQ2mqEf/ehHfW6O/CXCBf/fmyUAEDj0xmGfUqFEaO0pcfPH6DeL9H2rwmYtQIU90j9LYcO3MarbrQHCPO2m79tan+QVIjzQ763WUuAyUJCRA8gOZxDNKCSVVmhZRu9crZFgoh+EefrABz7Q9yXDfFokbE4OdWwZGr9DICmTQ0DVKmn2xmocl8F4EtRNGrSmMyPP2jukEiD30jUvsLJvCt+zB2Ca1GoQrLE/uj7p/vgznQfw3/Cxk/7kwV4mVz3Kq6+ceX02OP7UWpr4RaPhYNrfzDoChI2AwOgGIVWLJSV7rMJnGcGrHSrTd6k1k5nz3MtNkscOqmhB/h3PSvKd6i7QAxSDmKhAu73p2F8iVUoFqXzDDzZIkAKVQdfawpb2341CS8GYtdqbm7T4Vu2GsEHwo0bzC1/4wmE36vvO85HmVc8PVURV09pqIJi9z6bAkHaLhqs+sOsrJKQ1IUhDCYiLJs28lT+lAgzAN2lelVo+L9sxWlzsH5stwLGHvEfeUyYtpyBtPl/lTZGIp2+a7I3K6l2lL8VYdf1O9inZzQKY1e/iiVgZ2CLAUCgKhcyUVuZSMbeYXRrbZGTKey3Dhjk0VqKmJtOngY3xghe8oAf+FDKFzmDAAhb9NPOd1bdYtdV7NZP7qXX7poQt63mzNRmwBuSHW97ylr1yEHszvShrmgvEAd4chda2echin6WErW6YaleB4wOw26hUfTUrt2UWJDmSvBzExzxVFcVfpQagtkSdUjMtQ+nei9mFFDz3GMcfc0pKy14q8t9kjVgsDqIA9mZfuJSRpaLRVkv3RI7pW4H/pZBJVZGfJhcehxLGASdGB7JV1rZodDkmaFNiYvPGH+11wUtEISEe9hhfjAxDth0zSrWJD0JHtwKIreSzgYskAtQ62KXSVbnoOvEUSVDaT7UOUq/aRfjQaAK6INRQXChyWadXRAppS9CmJDQu0sF8r5rrWtZYfWX2CMAXCj6uD1YJTUY0as85UQa+p6MUbWWhMqmUhJFaQ0NGha1WISG5qNpHPOIRfXRJ4QTSjlOJ5GebdpBpqn4IreWLrRIQ5H20YIypgddWE5n8vE197jY1WrZbaBEXCPwAcIGq8LkNELK/nWAvmQUCvwT6FxnsNlfYmFaCnaaKx1BYKed7W31yEgAA0YB+aKrX9BWWmeY3JcVlleFuNRjZy2a00rJ8LvxxAjnM6Z3udKfeamUHT7MMNp+mWBrthkZcRgnMTQHR8ASKisxbOE9GnghbFq089alP7Ws7s3lJmr9K7R7D0Kae5LfqCKQ04XstbzoP/FUjSTZFePDLqdW114pAr/45ioUCJnLi5MaXSfON3hwST/IWP0yNZmLd3htoNnAYWAI0vpPSUwWkpZVa/dCqoA1Rw+fVjLbIlct0WWwJ27xqrlU/Z6fgkDqcDexNWj+UMNt1SbQUi0PgiExpgWEaC6GbpxAGN4vFBVOhAQwRZrI4lHLDYoh5L3rRi3q7r9Npgr22Qx2q2azdKas2afXEUFv6f9U/GYpYE+hsFZPUcZJ1dFG2YajNDrNYe16WpBIIatli+owZTbac/1UCh9wT0084/vTKw/9W0Nhn/TYLoqnWgpkNSlELk4YO0KFWJY0bSSU6XLXsWytnzbpEvgddtjVCVslXwuKQsA310VDYhuo2c2ZoblStrkpMbqjavbaQUEhatHMzKmjx7DyZLU9bEXM25UvooTJfPGhJ9W61LV2n3K4KRZbvkVmgJBB/DV/cImfkAH/OAmgsHnUnrTz3oLAllSg3kmQtldPCG4mv2QcW9ifYixFoxXQW6Q7UaiOanY/wJ1pzmqw3yEqpIXPn3+YkwBpJ1VM/Vq+pwOX80NQQCggUpqoBWyWDqcnEOAVME7xOYVtndlXd7xRetBUWjToRqeNGo9aSIGz4bgSEaMPkPA4KW/omOSuJKJT0BOoUZFlhU7M5EodmflBWEIja5nSsI3UL12pFNRbg1q5IKSxZ/kf+FvMPMwUfkovmehTkgP1l5XcNYhbZnDyYORxEgbIrUdWWdt7kHoj60B74PFC1gBG4Zw6svH+1YBXOeg/rmtHcH+/ZHnpUzOM2ST2ymFwfjt9hSmnXuohfe5jP5MPxwGwWTr/hrtGJPTrQdnw4VCMiVk9FfuCQ35R+llplCN6wBVee4pyC7GfxHhwQ7pvKcBaB7kcMTKPlJz3hOIUU2cDp8nAs2m2xmls1gWYxiYU5f4uf+SwoVmwK3Zy4FxizkBgpn6NYiKp0TBK9dnle98WDpKYdo2GtUlGfGinrMiBPQOHHctlUWlaIOBzaDhmhG3rVsi2hO8JZ5SZYGNogkHB3foCFxhmVEBiwSJyEFLDa1rMKW/porbGPQ7MWaj8Rf0abob2e85zn9FgfCwRUYzmhF+kWTit/h9CxoApJqy9wjWpr8W4KQkbgCp3ajg7hQArQspyFYLt5fCAuLAguC4eXe6MUT+2ZfTfmTV9exYz6XGYCtHL0ASFrBOSlsJk75eJ71pryP+53XjryiJZMLCD8M1BiUhdIMYsh3duolAiVk0monMUQVUu0NEbtxTE2073l1KsVrY9E0NgkyIAmkC3G5b7RzDTOQxvzTKRlWCCIBQKT6cBnYXRN99RoUF8tD0w2Z8ZEEqnDrMjktr1OnPoiYwZ+GbQfG+vYvio1R9aHTtk3JKvM+AzqTnGl7IzkWtpYm9c5NHScot+bdcRzzWj6WPDUOWWOxXE4hIEBi4NWgy0As6NGi1kHOi8ltAgmlWo+BYPX8MUQHIRIrSup0x68HpZsG8VhAaymhagnOtkuGUm3TmsLcLayy0MGFER/ObQt9+CAEO7VQbvOppLdzM8A52wg95ZkCD9HHtmUxc+JIPgZYGjAICbjxVf5HoGT90ZGgQNPFmKUPJmERv01OOcUEsu4zZlKcp7QDjjfRCJZuJxFzUMBQSa4F+lsmY2HU9jQHGoNp+Nxj5lA1uTbPkpskIvUDDWvFnTUQtx6jxUeqprX/+c1Fp71AY2XnGiDHdvr654kw1maD3loCorwL3PyXh60KQHhao0cUseoIppHI1z26JVaZqCINsZPJvgZhT7ShPIQ/AMai9OXA8hkcerDwcLlb5NqkhNEWoI25p8tKmwm953WhwbQ3Gs29dHYRBfI+0cI3VTnBRDg8BzVcV40M1CfkwuNi2/IfWg2c2iIFeg26/NwSOfBvGLCMGXV1Umh2wSd3ICHdSBytvxPwqwgr/UmHAwGnUA9Gg0Q0hHWTjOCJ2dGuTC2vcIpJFLBMfeBM2Kq9Yt1btUy7A8T+kZ/1DLwVYIAWo17E//xSm3BZdtPNQr/w9/w/4DXOrh+Xmsjx+47NR3/C6wBIC61OvvT2ZLUFvL6axwa50BwGHBl0G45KWaoXdiUSfqsQyX/Cd7qyKP0O72sUwDGGctuHAbogogTXZIRUOXrGBrq8kFEVS996UsPcwhrZ8j0A+pgimVpP0IyNr9zOgwbAfBIzSo+GAKV96pAiQ95/zmSB/8IoXXAWBIGKuiZUerQjC4deNYRpozt9WXJ6PdaVKJ5leXsJBd+xzPBeLauNaPRTeVU6zgB/DZ9eA+xY450UWy2zWik6l8eIWzpr6H6SUNkLWi2v2LxOLEk6CsDt5461fEqHYLqVD9/FjAFjyIwIFAhaax5TJKAPpxptszn2lwFfwr8Dd9ISCEPUAv5z+dsRds8M74kB6H6i0nPUsNqZp1pz/cIGvcGj1CIJs3cJsZ110PDs2FJyCgwe9X+x2aUcqYWa0owYZDQwkwPs/+YEiAPsCDDXa7E1xBCYAbgkdYMpHT+1+lH20LITQUhcPhrDN9AvYMDpS+kT4GAiXyrLWSdihlRyIGWRnhrzrUVfSb2N8R+5XcIGxXlmk4PgPciOJ5VaTnAVjY0qUAbWLdyp5umJfE5CBBygftku3sFzTa2HBLAadEJLVIK8KFk5GKaQLSRYDRYEiQd5sDF5pBeac1CqEWr6xAeU3NWEBXgmUovNpT7c7aoPSuc6pcVQs4idcAavwPohQiIZqv+RmJZVdjqZicsw0XZG7gfJt4BbzZWVps5zlL4wwS3goh2Azqx5jYj8W20ZPX9WXOyHkTWGZF6oHkN60JAQ5DgulUI7FBymYg8AGrVYgqYb8jPmC3SEwQHLUrPlAUpNR+ZeBgVPphyNhQtzMbISHCAh0KWU5UVPomfhO0ECPiCKdg+T5qvfN6W+5BVS7wn9bXOP+XehECINNMMqS14zRoAQGj8JFD8bFeRWOC2GhCiiE455ZQ+NWVrDSNrzT/WBVNLV6tM7aXGn/kcaDUcQQC6DNXFVBzrA77G37kJY8UiUwhbJt5NC/E6/iWm1CYpaAfztWo4/TPuH5iD13kGNpfFIWRHkwOe1p4mWS/bgj5Ss7QmDyfYbCSa2Q2hGDVcajVNLr4xQpuZiWSwbEvYWAcONlVzrrE9QXRbaJWKbIC3JeZ6mLD5DSEuERTBgY6sbZU4lTb95QNRlZkYnrpKvTUSO7MIprowLxRpkMNFE6QvkX6bC6L24HvMG1E1ES0wSraZSHM1lkFoTdXzNTpvU86I6bFLABvlSHHNuVkND4Zm1zb97EtN0VXy56bbOfBZsEDw2zwomSPnQoPbtVKeX12z2Rvj2DHxg4cUZFTgOJ2ofoSOD0SjpPZKAZty1E7CJ5k0TjIhaRKaRqOlTKkY+YFZmUWwS7a1rQQG/B+RlpRmSZeLgLq1OWL6UnzPgtNBgAQ8pp77YUMQLj7byjTJiQiawQFBD2Azbo1jfVodHzdNKc/gh2fBb0vmrj6xh4nAEvxVGlftszJzhkHRiSbYNPEpeUxsGovCIvGBnLZtVT6lY96q/iJSQ+BwTvEnHR2Jb4G2y6nDmE6eiRNIJEs3xjrUQ2Ge10Gpxb6ophTBJfBg3ieH+Oijj+7rbj0QagVbxzMTAlOPaQf7Y9PGJtpsOiJNYcPNIjDMbJLyIfzBvVO/AAuosqdZ11mEAzuBqmhUPAthUMAbowk4hWySfdZqO81NgoyZd8xuikIhtvHkIABIc5/csxupdkZj4LTTkQeNZtYg5zkktJDRZ4sFUrHDVu6X94YZw8x6/EsCEg6v0bEF3twzPg+aEP+IzRU0z66fQ3DLpoWNgJCcORG17pXAv749z8H60tA7WSpG77NTC4cKhxRNYDCgysR88trxxx/fk/9y/vome5tVzlX2vRUGUejZVFgW3B9ai9wt0RPJdjYZXxN8EFYxbkCCzZiqjDozEGnNzGqlZBJXzLoCXsMnBJfk3ih3JJ8Lw5n74h7ZIO4Z/xF/GEFTYGur/m1WZKUmN0gg0LLjuIGCbBbrUVhf4ZqkYs1+IK9F0zc5S+JraAf75tNpkg9ETWZTuE2Z0HzY9JGEQRzKkfQgE/dsMBEhzF3MvpNLRN8rGbHV27c13rsVMNSedna6FKNKVg1aGIwSEgNAMsRKtCwHONm+bnAGBtnxcRt1tDUtR94cDSxQLTTmiHVeI+jCSibdSL97dkqgw5CU5o1U7SbezS/yRnwgGzf1qJmxACFzljl8tUItWRSSgzfILWbFU95zLa5ZZYaVi5mc/jS7tXtnNph2VkNWc+VsMDHLVqH0toumqZvA1EsPNwWYmg0Z4e8Qtlo5NxM2HFJARIRMDptJbYUNFUkTZqV2Gx1+cphE9Y1qrWLlZA1p3dodqdauLmumssSuFeAMaf6h9WsNN8l+ebV8cFsmFUWD2VdG1HBmmJAVipexkiikXNeZz8ab0XnIsTNJmFRdImzUEuJ74Cxuc07AInOrVhX6VoX6FO8zFfuiguZZP7qJMY1Dz8Xn4tfjZwryE3RJfkBGQDEY2IGVxC2ovVtmb0aaAUBXNoQJa+k6XDiy6fwddHzc3IGa1zsug5hF92GdQ8Tn4f8SeAnyG/ErbAigLdOYDlPrhmdvRn8u0G4TxYlqixQT0QH+CjTudmHbL4eh1XSn1UNu3tyIdbQ/n0Wk/IAHPKCHx8AFU7OZ40WGUFzAY9WnnN0EwgbXPEmH5vGMSpHqvSRs+1Hr1bFLi7bWX0fYFG5cqBQ2WSxmFBQ2ZAmsrQZas5sAfwJwVJvpBEqHwaQibGBZe0nYdmuL0nX69yZpYJk5DquuhRExMI1zyoDHxNvkO/IaCiuFLTXu7AYAHMFQbCJjoYYFL7wZZhRMSJ9tLzfH24TJ3YmAKXPUi5rSZT9PWIfmQXQZwFczy6Rfz1eyTLRBTWHLQzADLeGPk1tUswl3ZH8uAgRyqHDfDkzo7vPnWqSIoaaLy5hQIRd8NjSb6UtBXRELTCuFLwQItL2v0f1MDePUIZX6bDI+Mi0B9AE6nMTJg2v3CNxQa9Z1FEMKLtEoabacV5ZjiBBAUpp0GhD6OEzYzDXCvRJnMwGv5ArY0feBD0TY9uqspzOCwNWMwzoClyRIyA4A++Js2UJNyIwMA8QDUpp1ouNM2ADiTEUYFFhZpdTye+g8OfDs4Np9o4MqPX8dZk4GImQQ7FmiZrOQKMs86dYk8J/CPos0UH0wJIxC1WxqNbhhpCL4wANh2xv+2zoF4vV9CRJodkOGwMjT2g4zTVo/olaHFx+h2bh4I0h7cvSdsCuFBJYp9hjnj7zXOoPpD67twSqthourlFUCd8H4IYg0pZlliDJ2aUkGmwVywREBgkwHOOa0arKBSLYjR2KZHQ6GAnmSsLY1vW+/Ivj7RfASBB5qUzaUd4Z8QY2K3ZdURmJs1lagsODjSSJoRqNUGFGjaEMZMRTZmPhsMF1hwyK52WFxjNFwsOG7b7xQS+BSIFuV8QgQhddW3WnxErmgpIA+MfaAqTUaMx47BQ1oLXpfIFjJxrSPGAUNFGIA7O7UQIyDaz2guRVEzAse+Bua/dGaw8CRC5lQ8LCGsHixjvYmqT2VZzeD5IK1ob1kXqoefWNHOAPuZUh8MPNz70esQ8JmfxV4jPQptquAudDE2MBpsY4IWqvBzKHsS0vISiJV58/Q1pYG+HP4bZDjkrhX+4cdXLt/tFAK3BD4q1nF/yIFRfaAks6sG9X6UbnmQGM7d9bc76Fsl4WqBN6QwyZoJ78cMA8uE3lUk/FDA9YOrr0BkdQOBrX219fpUARLFwgsq/mFPaiIx+qBVlgTUgXusIkm9OKiX4PFLumzGdry+otf/OLZvMlWfefBhu49wWv1acmBIphHiBpU7NtcUauHhqPmle6TZJjqmHavw0bJUEeJg0dnHxu+aZ/FUki2UvVM5dLYNL+Da+9Fqa0JOzYdoqaYImQ1m1bOqctAY5QjglTUCrSZZpP1wQV1iKpnTClBgr0pbNPJh/CmDLIA4NtUy4WDa2f9uNRsmERKAWD8mMrUyiFsVvfzOyweJZRDsnAobTVvTHdoTKmJVfnlBAeZtsIRdPTNgfncf75cdrei8k5fXoQC+ZCpy89Yw1NPPXWWORgdumEbAihEdDvMAVm8mZoNYaPnByoT9Zo9zHYiGh3L0c6ryNotuNcU1V3rFH+P8dzAX2lXQcsI/HXrDhy+YRE7ZaCgFFmQ3Q0NSjOzz5vTCMUI1HSV2X1CXwQPpBjOEgKXQ8J2OmVVh4gtM7lu6nsdmxydG7KtFlhDeNvQGnLh8DM1WXKkfppsblvTn3jiiX3XpbE+JEcsMDkw2n4C7uZgrFSbfBBqFaYIjMwMkWv196ZPKu9tA5b8nDrs1oh72Wr3alZaNazz7s/PrpSd1gC5VvutTfbLzdldeb/eA1AGe40mA0uzqaGNqBHAzJmPrcsRvCU2Dm4bI3BIrDo+yJ5tdjfClDKOB+cxm9XV4aur0lpWqUj3s2xtQF8NDg90lzqCJ0c4tmZr1VlUQ9F2FbzqZOdn8T2pHAIx7g2rwPf6vVMMQFs2R1rHC+TMBccJOXDDPstaOSNRZIWEgMONhwSu2ZqKdBQ5UO20KQl9OIQNQTzhhBN6VmaOc6xh76aFLbscybui3JBTBkgNu5Rmz252zgq1z0ZmQ2r3yWVrK+37a5eknArNV+opOaAUj5BjxjLoVC8z5GPdqDPHVWbLe++V+2ftaI1vNyvBXM0oWg3hw6WyxdeY63Co1Y6SDjtINCCeswQMEBxEhmSTtKexr83fWrMONm1Gs/8tm0apIT3OABipmYDMhz9B9242WeFSo9X5qI4Ob5m4Stdp4Um5mdmnBI3G6Qcc5ZByX9wf+BVuCwfDg1l76G6qrUMViBQ8LAP9cRkcAtyFNksTikaztSkJeicH1kN6RLqq3hD/CP0bIpxZBMfiaEaRbISOyBXHUO2WTNFtRVaabyq/6ENrgxzxH76HzoxfgZbL2fK1Mqk1c76+3mpK042MsOQwksimrSqbw7oZdBHdkQYiBYgZqoNLNhG0VO2TXZzUcFgGrRvC5iS+nDVKsIiMUHPsAU635Ijc6NBNEWmSTdCUSqgkGlEAuQl6tvFhwCZGpVN0Cl928XhIZixBJOC+SJ/YNdMpeAghnCwELnPCUmJqn7ZVB4fYnBAzzf/QkIWsC1GbJgghQ9iAklhbCsARSPzL9PU2Cdn4vmpzh6PBxEbZEBigYDCX5skNFg0caWtKqUAt+2ua0VYDEb7y0DAz+cBjjjmm/wCneVibgHTLYQI5Tid8m6G8D4k6J3DhBJpeQ8isbWSBKEUDfGRB9atqK4Nc+Jb2q9NcfJ9kTzj6GrMO4ZSIDU0go0aTxJpikrgvAHUDhgpBbMoi6Kf53PxOV4SJLpJnk5whzYi954DT3DDzqtmKdlTYlEoWEImFVoKWED12BGRGJGg3q662zQSxcyQLRRtT8ndoDVt+2ZbeBjn4maRemDPKIhl5KTQpOC1cqj5PDoPLdv0cPgItWrVDvUG4nORiwJUzXInoOASWSdYOQJvC2XxmDwrfk4rEr7QexcOqRcMN4EDjmpBdsDexwpsHb1TYcvAEdvvkk0+eSTSb5thCuW4sIOaBv8PJzYbDnvBN4kWJSdGvFrOpPwEuxL16MIignZlJlRDIOM+IGW11u8xWqKnBxlwEfo+gUUDE+/OZdbCYMxnkhumOOB1wbOLf1Kmpqr2JjtlLDq377RAW/TUOLt3P8deJqN1fB+OlVRiFPhLNxp857bTT+qkvbKK+m9VXiSRzMjkRTiXOPrAtLGvq6IoLbUWUZ9Yjh6TZYt+pcnzFh2OuAxE1kSpaxSCn5XcOtTOQzUpPMuACghQiYHqV2WFAITO6x/d1JCQXvg+QjX7eplyRWqWe/hWfzX4zzNbskV2sfAaVDEGNlXYZzdZW/80AoXLTvCnsN1NUkGROY0q5SXrnrqNZKJwxz5qzBTYZMAh9cK8MDqHcDFMqAJmpt5xm7PAyTAanmdE9NHsmekTwcAuESjLCypb4/C3mmIicQAnqNH4uwmRbKZ3rHIPO6/qWdHOkI0FOsqnQyiZxNrU2z8EsDA6JJj/HBslnRPEwdwItmAFNms4E92edJ+edAiSXaMqJxTl3SWiB7/Hr0G7UMfBBbJIJ+jStmzANUpc5VfQQA2ODhQDRT9XPxQLaWsL+c85iYgFpP0EeENwLHxTBwyTqtGt2gIYAZ+H0oQmYDkgJGy3HNIuONnIwmkA4h4B7AaNCGEkLAntkLe6yOd1VLUE2rebzAegpVDcHnmsngZZ7ptaAZxY/bOXGEzN0/5soeKpY3oy0BeYG55qbMFjIrwgbkaDVV2gFfZ40SVNDI3WUNffL4eA+EDgOhyN7cgCcmJGzrBAStBFakYMFxZl5BaTkiCbRmMAmLDI/sx4IGC4G2Jmji9ReORBNU4Swmcjmwm9EkyDUdYTkKk2kF/mfFm+NzwZwJgK1us65WjkyyK9kDBiW56Ewc1ADp1o6eIQ5yhIsnWR+BgbBTuN0u2GaJ06tp5kQn0kgpC/SjGbgURd2Kl/EqJDPYDHAtsQJpcJoFvShNBUW3PosDvfFryIAooyRi3CfQ8Wz87ycdDVXRpr6hrYfM4KX5YqgYbrxFTmYrWqkRddoKFJuWQ+FLWGPOmbcaFMf3b3mMHEYmTydA9xawpZY4WHCVtkSVQs5upmROG6SJshIz2obzARaAW4T5kY1W33Bmo9dVfgyisZ/0MHms8ko4ENxABAKLk+nflRW/tsIMcdfaj7UkLyHQqSwSpFmMyyB9O+dZoiZ5ntbgYJP4WOy2bgcdd7puk2ZU9sPWRFdAiAaApoMrAyq/IrZ5+DCY8Q/FVNNYRoS7sN8tur81nyZDAqiD0J0Fs+wPcdEuvjcFDlANpvNd+yPYF8KVrIqVuGWVT8niZzgP/CxOCR01+G+jKC9NK8ZQPhMHiCFUJ9V9yFra3k9IQ5xtBzzCEiK6SVPSyDlqMTMUizry7a0WWWotCbRyPABruJAEhRYsinwrAXgmXjdCT9E3UnZmtdmdTaVr9WRMIWON2VR+JmTiM+CU4upcTFNY5mkd9ApU4BJezmErKW9WvWm6yShXWQBSgQclc/0ZwBqpw5m9VgO+kow2JGMWdaYze8URv4GrcUB9H9cE7MECBrwBvQtfOCk9gwRKBcRvKFhba3GP+msm5KkHhTflmfBKhkEGOBw8Vz4cieddFIfSGjyayXWvPttDiUTWc6hZEam0MapUbCEK80Rm4iNJ9+H2UA1M1rGWVdVo2XyfhVnd4xazb2jkTXlRlvAM2g5hM757FyCvUIlqQHVTKaY9O3EzJxPz2YZyTlsF/+OjAUkAA6rUIG+5Zh2X7S5co0C62s5YknLgm9Ohghn3zZp+GmC0DyDrW55Tg4qlq3ma5cpTm+aJKGEpJwk/wvtBpbEgnJDboDzElS9ONRQaEgwiyqb7M70UD3hy7JFhvpZaFK5d4QOgcO0g4eRzyWS5B6FI9R4meKypFFzaFNrmS+6El5sHOYaGIV8J9EmGBraNcmkThjMdVhF2Ko2bI1E8uBptjl8QESMFUerWczE5YHxudTK9FwGh8v60mWp9HOnsamNciYnGBSRXkIf2XtXhi+bwsKTIIcjlwvDAvCeVdjW1Wop0P6OReag+DloFw4A2gbTBq8M+MKpywqdwYIsVSM1we1sgmfnJzAo/DKAcEwUAi6jpGocDzWbr6uyTi1Ei1VstKlw8BkIPn4sEbFUJ54T88kzCTrzrETfWChqU4xevZa9z0PzfChZmy4Wr+F44yjCZcJcsvjcoMIm900fDg3iUNzkTLkQLV9xVQgkR2/7PryWNCLTS5h3cqNEY6S6MLEMlaBvLJoJkBZfRd9L/4ufMcPHHntsr+HJAICoI2BoMcBe/CHNeF1f7kVN4/16z6sKWj2kddiar3HogaZo7KiQGYlrOnUj2EMOImwU01I58Dej54V9tvyjaj7NmSWWxfdsEsNYaUXOqcZnyb5dbhCaD18HjI7sApFMJrn1C9cRtvo/SW/ORDP3bhot6UGkpuC4QdXGr2NxySIA4gLgwiYhYgPgxSwSaaOtcSfAnHD6aaZIbpOMg6zV5MPlDFMT1gYJyRBeBQJSsKo7kmMz+T3YJ4cKsFrtbbStZuMQIWxocSAjWCscykoQ6GL+aZJLl9JstdlIMiCUah4CU8TCsgmYSp1nblIQU6dagBR1zEYSjeUU5Dp3vQYSy5rTPNX1ZKcmEf2uoxQVQn5HwQynGk3FZvHMaHZnhLaIlX5+Ymhq1TxY/I0ad1WtplbhPfL/a3MXngFWCYKGNUKwDIy0RgigBAF+x95yiAwuMgrNCrGxhpCDwpazIRP3qekNF5IboJyPXKTQgU61OJVwgcPXiGqIgsTfxhzjead83jSTpNDUGoHs3NNi59ZnVfhydHg3Mk+0snzz71pdhOZVbo1hjHmI0v2RZo5WYs0JioCt2COgK7MbSYjldfw1XANbzNcku/7aIkPaRmnhdVJIq0wtX8f8OIpIyrisENW00AinBT8H4XQwgw59BgoGD3U4WKvkbhFtMPT/Y4j3FGMVx9D9dbRY1eKpcUw5KuhYIMw8VVIwd8QQ0WxE1Ggx2SdO0cbHxq/DVaosjvr9MtmOQ1M8MAKHD0OIbEpICER4QMDUh2MGEvlL/JsaqXFC0Xx1ckmrRnPRxja7pRfJqoB19f9qANdiLmPuISUQcRNVJo6oCWU/wAKxPOS9CYogfRLMadlao8xXWc+1KMWmLFDXYDA4zqQ9EKZsb68ZNTrlRKHhiOBYDNS8/gtXbds0b+T1fup8WetPW4csTXu6GhxSNBlrh18MkRPTiQCJEUoSMEOg9bEBM8wP/DT2IS1NKz24NvSxqDZIUqR+DBACKQ0ChkxiS70xoW2qB1iBqiLwKBxxFzArtVbVtnu9fVUWS7c6Q3rYfXb5gwiJeWwAdUBr8UCT6plg53dHHXVUjybA0EVAEdRKxkhBX/W5VhK2qk38OwQEXhRYFYKEs6nPhrYjCpIKbbrHAWzAIixSYmW1fnLeaOv92saqVVSTvxcZ4CtrePrpp/fjOiWIss5iocJRjtzWdwOIJiBAWGs/kjzMq4Duc+tGF+2tUf0H/AScf2eJGzAk+U4g0ZE0ZBzA4WhESP5QHyTNdQuB31aLqZ3qjdayIrUxTHZrAiekih2w3RpVAzWJE4K37I31BOwVmhBBRdhMLdZsxyJtyiYXtvQbUs2qlQiXMY2Ez9J6bHefFB2LUYRKKEABKIUvBaaVm5AZjFY7qlUpSrt1KEYi9bWgOFtFIBgEWWQt6PxIPUVO6dFcerjNYSOABA3QwMl7ohk95DJ9pvSB1xI2NU5l4armAREhUJJhwHTykPYLkf2JIBpMZC4VXwNcCD8uzUYLqN2PQzHUWombZfFzlkqa5yW7QSBgJoCvkjrFOvHLshYDiIP0GhBUTfnJ2J7yWdeebZmLJWLuqcPRxBcjc8ApMgKSnoRwsTAmtdV4+HtoRcwqE944dSl0RsH7bTJgq9oegTNCz2CAgwgORroMMyhV3aYv1hHoyiS9G4gK2hNYGhVSCFb2Vt5U56lJGpSI9Yiye8M8BAwD1DQwh1QW2RUImgwDOWJOfON1eGeE4pw+oBUp5n5OMn9bRbF7DQoZAm2FQBRGMDD8YvKW1MmyVtC95BeaEWBdsRR5sAF2MZ3UHLCmMm90U4aIlzsqbHlx0sDaFIAaNeHDUSGOtmJhpOrUFgnSlGRYWP4GL4xCYtqeJ4CZmyGDYj+YVV0Fu2paUMJz4p5w+Ej72fTF6jEBW4SMr9ZKEHnCU0MgYbNAMhA09/PMfSe8UnPGOy5sJoEt2BCc1cGUNYLA4YfBoKDgI5vL6cdltZOmlp9ZqOOOO65HwmEtWL1ey8X2A6gr6TPdBH4mS4NLQssDaE1Em/q5CdYqdBxk/TO0HOlEEutEnRxayQTipGKb2dBxKs22VjRancmaymgVtbhoEC+h6XDCTNzrUyhkCpwD2riMnqjcIjVGcTCUHrsRjeVLx0DfeSmuVQuqF0mftXK9Hhz9MkwdWRaqscDOOHiuSR5W/d6cpmg5HuV3HFSKf8zWZOK+9kSe0nwmpDM58j0v6kIwcErhwlllb3SEJgMP4iSCfFuLiZOLKUAA+T3/A/mPCAxt6Wgji1wqHjWm+caa+a26CZlGG/vdkKni83gmokx8VnAz6dqmAaWvZ1rQZLoUd15nnSCFkt3RzZBrV5vKbAIuWrj9wtSX4CwnClVOLYDZBkvgssjCXh06uDnZmUUlqmIjMA+YV/A5IuDanyO1hpGyCz9U2TXWTTLfa0iYEyMbIhP4OuvBPdtmC4yS8QBocRx6K9dyCl5qf9N/ajXWyoiedaHuAo2m6cwGitvqDjq5Zlukv4QXPgKCQeAA/QWMCBxITA6Um8U1ctWUGr0KFPMz/gulg2g6SvZoEAPIKdExE9ouMhvs63mya+O/KljZ4rSygVubVpsEJqyBLwtzmRpStBhChk+LkFDL4JyBrHuwTlX0X/PJulkkzSGkZwk+Hs+vL8bnGchl45dt9Dzeumar5fgyZTGraDnCeJ1eGSI6uJxu/Tk1IIvLhWCSTJbWDFhJQQ7N9QgmRMfnTYNJQqP3ZnTdykvW/HAKof/T+nsbudBlAPYsPijzwBAwhAeqjy2q7A+SkXsWTLMWRJk8P0KINgR7w3J4GHyOasI30dmyHlT3mvvYKkLuJvqQRl1Er2BHLDwm0bpOm74YzidMYtpF0+Im2JEIqhN4EnWR+CwU3HDSCVDIv4KaW8M5ZjZTcIzUcrNaDZ9ri3q0CZXnOPrcAxXx3BP3Rucn2LM8n5oqSwezTDCLo/XbOGD4c/i/NLuByMrzZaGN1K00+5tgyrQOm5qf17ZKmzGPZ/1BDshQa7ApFJrgixGuZzvV9FfkyfE6wiWLQQwve8chuAgf7BKgA94fk8Xmk6FA+/G5IPKYNcw7kSAmSBgHs8/FvSKkCJBDM/jK36Kt+H+AbPwk/C8iQA4R0STCwHNRSILLoE/q9BQER7KpIHeraY0whxE62QBGCcC4seVoJsyTG5cJ/amhoipsJvS9tm5G2Tg2S7jCMjsWSTozziyV9JAx0U4sKItui3R9O4VLnKm2SLBnrQ2INcf8P34NeVsEENYwgkAlFRoQkw5NB2GkmBfBAWbBNGH68Ad5nQtaDjlg8CuAZ5LhaC0yJrwvWsum0gY/4odZMieTmb8zotRH5eLeFT5eJzOA0NIJic8nerWoJk2+vmmLhzZFJ6mxCTf12pqPVk1ptnrIMjfbqwICo3Hwuwj/EQrYvTYhRBtIXcqeG1k07NfkdGme9IfQiERuRH2AzTBPaKACe4LPJHtB7pH8LuRCqpOIoBEkXsfXwk/i7/EVAZ8RMLRpljNmJN0ai57doNTifq+LYMU6n4NAkwbkENQyO9c4I2R9xSkDgzTFFSpKwufWhK3VGDkBYf2H7LTt35iNQKMgdEStgMFsooW1CYlkOwQ3VnOaBTjZsUhH217B2cjPFgtZHZ8djRRgLwMatbDkUbVuRpGCsQpYYmVJ4Vbo0MZgZhQL4fOhbbNRclZy1ebTLaB9ERO6yBC42so02zN4b83Ok7shL1jrOn0ItB1oOuaNBDRkS4FeNte2nFbjZ7cheV1ucM69VwiqT6hQqQmriVaQU1PVdlt2tsw5DFXw8rOz1YNtq9C6pKeAdXh2Imt9SAkQ+pUVIG5hglOmoDIKT0GrEfyOaLZ5ZW21V1kukikcFptTTTIapxjThtnDDIqyazadsaXGsJ9aDn5TgNJ8pdbMnrL18j1S4NJ3lBmb7yGEoXCaE043APOOFsNkQyYlmJFqJYyRhcI5y2Bs3tam0lC1dWqrZmJroO4i6YyhhckHSNVvrw7SVaS+yP3hb9k+QLOZcEkKU8uHqkFGFcD8myp0qe3qlayW9M0IBDggjhbiK1qMZ6G9PQEKETJarB7GmpKrs7U2Te6s/lidLZ/me9cI26IgYR3CZfqLjSCSZVPoHYfTTKqHHnJAJwiI/dL4aqO7bO+VgiNNxyude82pJrmazPw7tZlBCp+rHwfMgUYj8iQoIWOAP4qA8QzAJ+CAMFtqlXvF+jatxVqZlDSX2VelVfmf/7dnKNOtac1JhbH6G6HD5MAKQeMRybKRCB/AJwwIfD0EyShPk2tayAxGDQgU0OzdZpVYDRYMNuxxxmdi6mlTBZCLow+0A9SCL0Zel0AIHC+d+Qyg6jyGVdgmywQD2Ra1lRGQMZ2kyzHNtyc029hi5s/JtLA1FfgTPh7V90RxpLGg6ih4wCngeE7vMzLMSDavGiTY1lQTacki7wmWh3bFNPKZfDZUd3wwMhkAyYDHtYdGDusdWodF2LSLaLux39WZCdVHq3UorX4qe0rYhhoUt6qrDPvrCEU7L+Jg058MbApzBXBM6RsCQISLMJBCQjBA+ol48QNx1tFIwC7gaFx8zwXmhaYCb+N/SbdhxslSoLUAXMkiIPBE0/iZaGCjx5yIl73qxoSpVXU15F8tWgM8NCapRrL1agljhWL2jLAtYypqLWUGGFl/qmCy6ZAAEAIyAwggTjlmjRQTeUyyCeQboerA2yfJzVd+5nW0FJExQsX/kqJCsOjUyPvid6FhhXKGDlRtp7Us0XNVZm0KSUvYWo7/EIhbMbZ67csK8tZGZiJ9yO8ZMjlT9RPZ1HS9dd533hyFecKWBet57Wthm0edafkcrcWpi1sjr4oBLiMEQz7UJnCwddex5eAP+W5DgpZ8v32n2VqbOdSXrTbjS2GrHLXM9Q35LkObVDdnmShym8LXagQ5RiJtkU1rE8V94bMtI3AtFu2YkLTSOmNap7UZFZPaVLpo2ehyrE+c/m7y0LLyPoVq6AAPddfcM6Dusos/pklagjX0+hgtvHYEWBZQXWfIxphAtSLIRUdBVtKnPm5Lw1eoY6j5dl2TfafZljWz84R1yA9ctHpqUbO5rMZr/X9lXaTpb2nkhF6Ssm7HAfOtqaWr75r/W6ctjjZwPiMI2jb8nuqzLDJEbF0TW9uLpVC0Pl/BypkRmtLarDr92qr5kuJUO73X6/8B9830ETERqFcAAAAASUVORK5CYII=', train: 'image://data:image/jpg;base64,iVBORw0KGgoAAAANSUhEUgAAAJsAAACdCAYAAACjOAqRAABCe0lEQVR42u2d9ZdsV9GG84/wA0GCu0twd3eCEyy4BbcEDQQJFgIECBLcPbhbkODu7g7r8D3nW8+sd+ruc/q0TE/Pzdy1es3c7p7uc/auXfLWW1WH/Pe//+3+798hPv7zn/90//jHP7Ye+drB8uCeuc9NuZah54de20vr/K9//at//Pvf/97+IhvAC//85z/7F/fCzU65xqnC5QYPbbSfw2PsPb5vbA19fZ77bD02fW+4Rx/bJFBtxu976fRMvWEFriU0br4n0dd8n6/XBwfTk9u6lvpZrdf5DD+nfkYKVl7LLKHfpP3x2reZzr///e/9z3lO3CabSQVAjZ0b6yMFsbXRualDr1VBTdPh+/n9r3/9a/9QqFL4Umh4nmtjP2ZptL1iarnObaaTx6b4MlMFamgDqiBwb3/729/6BwfK+0zBcx14zx//+Mfud7/7XferX/2q++Uvf9n9/Oc/7372s591P/3pT7uf/OQn3Y9//OPuRz/6Uf+T//P8L37xi+7Xv/5194c//KH/jHRJ8vtT2FJL5v0ovLNM6V5SAodoOveSoKV5HDNjY5vB+w2A1Dq///3ve8H6wQ9+0J1xxhndF7/4xe60007r3vve93Zvf/vbuze/+c3dG9/4xm2PN7zhDf3z73znO7sPfOAD3Sc/+cnuK1/5Sve9732vF84//elPvYANWYuWoI0driqge0rY0nTutZOir1k3KzckNQWbjkChjb785S93H/vYx3pBedWrXtU9//nP757+9Kd3T3rSk7pHPepR3QMf+MDu3ve+d3ePe9yju+td79odccQR3W1ve9vuNre5zbbH7W53u/61O93pTt3d7na3/m8e9KAH9Z/xhCc8oXvKU57SPfvZz+5OPvnk7h3veEf/nV/60pd6YUQLck0e9CHfsSVkPrenhE01v+kXPvUgpL/DRv7mN7/pzdzXvva17uMf/3j3rne9qxeuZzzjGd0jHvGI7r73vW93xzvesbvhDW/YXe1qV+uucpWrdFe60pW6y13uct0lL3nJ7iIXuUh34QtfuLvgBS/YPy50oQv1/+fnBS5wgW3PXfSiF+0ufvGLd5e+9KW7K1zhCt1Vr3rV7hrXuEZ33etet7v1rW/d3ec+9+ke/ehHd8985jO7U045pdeYn/vc5/prwyT/9re/7f785z9vmfqWD1j9x71kUnf9AqYIOYv8l7/8pReilmZr/Q3Chg+FJmFjH/vYx3Z3uctduhvc4Abd5S9/+V6IEJbznOc83fnPf/7+/5e4xCUOeFzqUpfqhecyl7lML4D5uOxlL9s/eB3BRNAQOB58Hg+e4ydCyffxO5+FEN7oRjfq7n73u/da8CUveUn3kY98pDe93GcL/1TQRA5mwSv7wjYxVK7azFPNRnD6ESaFj8XHmf/Wt77Vay98KUzXIx/5yO5+97tfb+quec1r9gKC8ChICAgCgFZCKPh/PnivPxU4BcyH7/Uz+ZzWg9f8DH76OxoQwbvVrW7VPeABD+ie+MQn9tf+lre8pdd4mFtMf0bW3Ld+tqa2+rKbKIB7wtazoDjwnm60HI43m0CU+I1vfKP70Ic+1L361a/ufSS0BRuohkGrnO985+t/svEIyeGHH94/2Gx+IohsvsKDMKRQ8X+FT6G62MUutk0Q64O/q5+psPk5CDrXhtDzGmb8Wte6Vq+Fjz322O4Vr3hF99GPfrT7/ve/37sE3Htid6wPgqf5rYK3L2xz+mMsIv4M2kyTAjTxwx/+sNcA+EA48QgYG4hQIWhsNgKhZlFL5Ybzu0JUtRgPTG59KKRXvOIVt/3keV5XyPx7PpPr8FpSmBVyTXBqR95zs5vdrHvwgx/cvehFL+re8573dF//+tf7tTCSbmm3Fi64L2wjflwuFv/n5KLJcPY/9alP9U4+JodI8HrXu16/0WoRNRobx4ay4Wyq2in9r9RaqXn0tXyggVoPggMevAdhSqFOTVg1m5qP1xRi/0bh5DO5RrQdviYHimj5Na95TffZz3629+8SR0y8cBMDvrX6YFOErLVIPAe4CmTwute9rnf273CHO/Tmho1TuNgkNYWbpmCpcdh0NpK/4adCqGbhOd6jkKrF1FxqL4VVE6y59Xd9wzSpqcUUYL9PYc/PRmMiyAQxhx12WP87ETMwCzAN2N83v/nNXugwrwn1LEs2SN9vVVpyLVqq5vFa6RajrMxfikF997vf7V7/+tf3QoZZYbOEHdIksmFsapq2KgSaWfwkotDznve8W2aXzwH2QFOCoaFJwM2AR8DdHvrQh/ZwCfDFYx7zmP5x9NFH92buqKOO6o488sgeRrnlLW/Zwx1oJCESAxHhEbVd+ooeDl5TU6oZeU1B5P/cG9EsawKwDBAtXlfXehFhMbM0lMrbaM1WgcmaPzTK8ubSJwMTYxMRAhaZDWTTjOYQLDZCv0sBY4N4n5uMMKGJrnzlK/fCcItb3KIXKAQJ8/Sc5zynO/HEE7tXvvKV3Zve9Kbu3e9+d/fBD36wDz5w0skOfPrTn+4fmHL+z09e433ve9/7+r8BKOYz8LOe+9zndk9+8pN7QUUYEUQiY65FM6yJTYHz0KQ/qS/o3/E7+CD4HdcOhvjtb397mz/XAoJzL3JvWpDTGMlgV4RtFt6TAmf6hueJMHX6xdK4OfAxTSYLiXCc+9zn7heYTUkthZAhbAiRJtJIUZyLDeMz0AT4eGgh/L0XvOAF3amnntq9//3v77761a/2+U38Qq9jCt2nlfzn/siPEj0C1iIAn/jEJ3pf67jjjuu1IUJ+4xvfuDeLHhiuUc2lSUWgvKfU4vwfoTPIuc51rtPDPKzZd77znR4KYm0zehWfy/ywwjQG7Ct0y/qBKxW2MQH0QmWYVDMqpEGIz4Khba5+9atvmUY2g0XF9GH29HFE91l8tRs+DmaS129yk5v0UAia66UvfWmfwwS1R2uyIQiXuN1YnjjTSJVi1KIHmXvlczlgCB7pKb6P34Fr0IgnnXRSjweiZRE6wWbuk/vg/9yTvqKaOiNp3sdzCh3mnQOEoLuu5mfzOmcpB1/P1N+uC1vLGXUj0kyqLfjdTTAvizbDPGEOcIARNIRMp90ITljA050/0QpoByI3cpqPf/zje+311re+tfv85z/fn3hwOYRLM65ACBIPESLdqBSumsNsrU2ynnMtuAaS/iTtETqAaK4VfxCMjeBH+CajVA+fGtDAiLUxAgcCwiK87GUv66NWhNsUHt+N4CGAY7hm9Z9XEd3uOJ8sqTwKm5vHDWNKETQYE2gf/BkjNbEoT7M+V4KwmlR+YpKIUp/2tKf1vhMIPFAJG5vXlAeC13hwLZUGnxog/ZyppMXW63wH35XaxtfAzxAOYB3TawgO96c7YGTN76a/+L9aPmEbDh3AML4ln813ck0IHf/n+92LFKaW2dzIAKHlbGYuz1PFc2g22Bcg//hRLKwmUgHSfLiIpoUyM4CQkerBKcdhx0dCgAky1CiatRY5NDVXhQ+WDf0NfNI0G3kngdPn8PWAMgBv8fMws7BI1HS6DAm75Lro6/E778c0o+XQ7kT1aFMPVWr3qtV3AhheuaDNChQUOnwX8pgvfvGLe5OH+cNc4quYBtLpT4BUjAxYAcoPsAMRH5qRxUTAWkzYIaJiPlfZFata9Iy063NDtQgKHtqZzMEJJ5zQPeQhD+lufvOb9/AMQiWMY3TOAVT7Z0qNg4uWJNn/mc98pjerecDG6k5WCQ6vVNBaaRO0V2VpsIic2qc+9and9a9//W3UHH66eJoPBczfeR/mEiFDi2ESWgBkZYkMRVpDlO9VJ7RbWr91KJLd4fOsI1obF4GkPRqNg4lQSTAwSGB9WCcOMM8jkOc617l66Ag45vTTT++DlayR0I+WSTy2PrseIHg60s8xQWywwP8hLuIMgzvd9KY37RfqHOc4R78gLFaaUH0UQVwiUkwCJxRhxdygyTipaEqFKzVTms2d4H3N85n1fWqToeCE1ziY+nfcI9H6hz/84T4fDIzDmpgJwWRW5gnPowmxCrgcCCBrD5GTiFyTynfzPVLaU8NuXAZBSCM3lv8DL8jagC6D84t/JazBQiFIpnZqcpznWVCgASACcDH8GZ1+T6MbVp3aahbXXXs6q+SvAq71vd6XNQysI5r8C1/4Qo/bCZtA1BTEdh1luBhMaWrx/8iMAAOxJ2ovPpvDm8jBUIS+K8KWmgzBMuKxuENtA+zA4hAIcLpMZAtp4IOZqvFUajrxN3CU8TeALlwIT92YdtkpBsRUjTb2nqnXZeQu4Ox9IXT4vQDUpNc0pRxg/DYJBq5pkg7Qdhz6t73tbb21yRRhdUU2TthYkAyvOSVoNnwNwEV4Wap90XAWQXTcLIDAJc/zHPw00jB8Biqez9uUQo910Xh05I0ak3rFmpCMxyw+/OEP70FdtBd+bxITzKeyptLdjeJBAzCpCfxupLB5yjRlCTVg6kgQYzrJC8rrl6Mvq4LTqCkVnOWkAvBC6wYra0VHq1yIvVIHm1GjGo/3sM7kZo855piemcyBTf6d8EiyYdB0CBwmlRw0Gk53yHVdZdXdyhZDpzL9NkwnjASKPTCd0nwkCeJnuBCkXNRwBAFoQrAyc3xDtZRnhkf6czU6VNO5RvizuByk6RQwo/iksJtb5jUEjnwt2hE3RcbvUJnkooHWykyJ/pOqGEcTIBGNpnCZYhE7M9JMtY5PB/pP1DWUkxtjKhyswta6fyPJ9LM4nMBBVG4hQKwxJAasBwfbyFSfWD4gygCTSk4V35D9tPahtqRY1JqstM0BJwFfDaIjxD4u3mhIle4NosYxnRZ/wMjA5+Dv0GiJ+reizE3yqXa7Gs2DJ2whaA4HkOwDAqYJ1ZUx44Al4XkzMdS6Aiuh4dhLUYVkiqxV2GoEqAlFleOnUUkO3YWbOfTQQ/tIk5siHSXIKOdMjIiIimgzgUbBTE3EmUGY5jlACfziu6HVdGMEzwGCwdUAdOX1cegRQDMR+M++RoCBwEEOqPlcrdbUKLy+b+HoSCeypnmg7wA4opaT7iz3LAmB/MS3gONFIEA0q7ApYLWSaP8xnL1JTFFcDitB/hkCJ/iaCAAHHZ9ZTZdVYCTwoZ3D8UNDSsvXXM8CeodeW+hUpfOowKHRAAipeQRkRJAs2EhWqvRmbhbyIOkXTh83ZRW4EdeZMRhYtg9a7pFwCdYBPA4BYm/YEwIyfiJ4RqzicDxIiYEG4P+JMiStahHfbWF/QR/N3Cc2Hio1kSc3wgkxAuXiETz8An6ivqFlE6ZDf8E3SAgleW/7wjQ7AhxiDmcWhzUm6IJyhH9MrhQXx7oL8U5cHgMITC8Ud0HfZPYu4sYsFRRoy6GtAHFAdcbJlMSXVUUm2bkpbpbCEfwCEsK5MOmvZXL/zGxGp1KdalOdTDuxtvhwEFTxyQR32SeUgilClIM1ruwbTBPQAbRbspTXEiDoCyTDFRX9uMc9rvfHshmLDAQhD24GYYSNSjI52RrZTsGFS/W9L2zTzNZQSy00G64Olgh4A3KmRd2ZaRCmQujE4CC1QnXi75PokKnKKdc3dwSUCLZJ8OOPP77XVvLQ8sL5v8UZEvnAgLJV1FAOU8bIfnAwP7skMwCuo8gBqT/gDcF2yhmleAFH2Z6C51Ect7/97XtiKmZ4qDprSsnfJFZDNWtKN7Yc80mZnYi0FeJZD8kNcFMUnuADECG1qOJVuKfw0fYfs5GDrPvwJ3vw2te+tt8786ZoMwXPskEUCD4d4Dw56mT6ZlZjVi3GqLAlg9QPzXb1OJ3AFeTVcPYRKDSZzqUsW08LSXiIe4TQakUvzAh0J9ih+4//X9+qSFh/uj4973nP6/fP6jUzDbZ9wDJB0mQfsWDAKCAHVdiS4r60z5a1lHwJNpxujZhPCXrm37Lyh4vkZsDSKF8zeq1Fyfumcr0mWWIrsNOznvWsHnOzbBChg2+osElqpeqNiq2s+U3LNCvLM+nCzAyYrkCrQWK85z3vucV3F6fJkjMjHQICagRg1FYu2hBpcP+x8wLHYWcvqeiixQQKQz/bICELpNF+pL/QiHIXBXqngL2TLgwpttSND0dDUQjLaci6TgQuWx6g4XAuob5gPlMzpt3fF7bd1XBAItDA7nznO/d7xz6i5YxMETSeI6F/7Wtfu9dugL3Khfu3tBlVs0mGhPcPmwPH0jSUfloWEuOnUWOAnYePlhmHjGQOhrE5ez3NxV5AwKSASCCePSRYECvlOSNV9h4FArMHuch2XWPFPaNRjCwOi1UwpeQ+MYvm2WwJpY+WF0dyHRWdPcPqcIl9Qdv9SJW9QUPRQOf+979/b07VZua2xUutvCctCXfO4C79t7k0m2bOinUFgsYrQB0kz9VgWVABm8MSMpxJ+O1ELslO8DRt0rCyMwtLZAiPk2UN25c9M7dtq1iFzYiVarh73etefU+W2qZrDBMcdR4VNIWCTAG5NVNPArgKm84kwkjrKSJWJT7xuf0k+2bVSaid2G+wUyyXaUcjUdteCI/QJoPKLgTU3Harx8tknE0bbNQBVRtgloS6uTPbOtk/jAsiSrUQlr/NVFQWyOwLw2b4baYF1XK2KgNfQ7AQumysyB5jxah1oC8dFi+5b0O1IZNOA44grQ2QeCTaErssDeN3LozoE3sO0qwv0CrC3UkTugo/cF2HYWwdli0VnIebmCRMLBKBnQQKFYsgPT4dgoi7BG2J96flGnKRZmYQCArAxxgIgSARkfClNi/JpsRcADgM783Awp+5gasKDGob1Xnzies6AIve8zoo8Go029sDvBNtAoVgTrP00loSNBvaDktHrtuswkLCll1/iDqo3wRVJhzWfos2o9HsC8aMJutHs49ErXmcd3Fqo72W5qnCVedXtV5PQa3heotzn9MAWwTGiqK3ilVqp0dJjnVWVW0R27qOrCtdZG0zD42Q6X9RR/ryl7+897/F26QkKXjIAEEDTW+ATio9rKIPMyfe8QdQUmBuWmAs/8nAAI2GpqPAhSDCnrgpEBWHWbSzpcGLZln8jwe/155ndRBFqyNmbnR+Dye91ZOt1c7B68r0DZ9r264hs9VqMFiHpbVabmWLrzrbdB7ssh5GvwtNhd9NhynJr9lSXz8dDfewhz2s991qj5A8PP280TGKMW8iOgFdRqshXDqLNurzS+Gtk2iHt+4X5Q3XZPsiFeE5Tkdhc2NaHXgqvifdhhOcQiEvr153johsdWJsddtM8kLOFm29rwpI1mjam9fgrFUsbOOZ2sRwXg2XbJ68dhx/aPt0mjIqFVe1cAlFA8iLjGTHKokWo8JWW5KTqAWclWQnZz0npGi7ea9jDVt9vhaFO9J01Y6WahADEQUPCg0pFU4njGD8CnxJWAv2083qfTWOk45r5NwqJxwLIlrTqRUotAaQAY41oDdEUnwkOGbUcZiHrt0pq8bis1hvm2AvywxJnIzv5DqplCcytYdINgCy/y/0cdqfIZweWq/pgLHdQ42KWWBqD6EHUVdgV0MT7tpwtBo+HflPIxqroyoXbtkujmkCU+1n6R+5WzaPRjZcFw0DWTDYqeB/dO+hxy4bTtSc7bXc6Bo4zDM8t3UokrhI3QXrSiNEh7mRCIcRS98NqNvUdOQA3pZ14Pdqpud9ZMusOvGP3zmcVMuJrdqGy8jUrkkoG0oxOeSJq+aaNKnHecoJbakldJCXU1LUbEg8Q13BZqykrtU4qxK2auY0I2ojtBUbyeKg2qE2EU1p7vE5IQ9gFhA+qDW0wNcpzn5y80S1dZJga7Cu/XJxNcAhnU5jQx38YJ7j2si+4HSzeRyerM9NALWa3mVGN7UCI37nMEKyZN3UaFyvQmbmiLWGGEvLjbzvbcI2FO5zk/whWoEvQqjcNLMH9oqg/oCFTJWfftCqOGt+Zi4UZsSfBDKYfFqBWult0xqiaFMvqH8WDIGkQzfmzPaoNZCZ0me2ls/lyZZVgSnH/6H9F9dGdRPXlfOuzC/zE8o27+fv+Ps05elCLAN/DHW9rA2uyZlCkpXlo5A58ohr5rDQnR23JVk9qcQOaWFf/ESi8SXYEHE0hc126La4gkRpBxw/r8IKywpamsxagIPZxixSsYVJz+6VOYDD6iEH0ALVEG0hcHC0aoAxdQNrlJibxmcCHaFFsRDik1Ln2SxAUp/PTuloZQBytG8KQUZ5i1qLVvf0KsgGWLglMHpZW0c4mU3g2h2GgilFMDNKzgM6eDE41y984Qt7Jm7CHbZE5zkkHRwGylEOrRg6easoxG1pYrIbREPeOAuSA9P0MR3ewe+8z0EdzMOiXI0DNnT45sEAky5NMGKZY/L7c8CuzXUSVuAwwB+jSTXYpYQGNbymGrPaMvtTha2FC2bUz08VD32MZfPKAkEuLAfADcDnFOCdLGxQicDNIMtZ9FBHU/MafSRwaI1esi/HTrQWrTMJ+D8YD6OvPQRq3KSpm1qzwY1pNs0WXC4GYEzJRAw1Yq74EiYIs4J5Ya0QHgSJtWSTbFDN4bDJizlI3RWeA8eyFYKQSA76bY0zX7ZiS2HjdXv5stf28K19fD3QzBlDE9b6la0AoS4wb2QD8X1YFKXZ1vD2VGNIF73A0IJ20dnJnGKqfv0r/k+ZGc0DVfFw5zVJ+hipTUwmW+fKcxwstFut6kqHf0jY0vfJ6Jg032mnndYD4tnv1iZ84pVZAmmUb18U1pmEN9cGtGC+2e9o9RJeJbFSVwCfFkGiZUYdQ+6aYv4rwJvKoZkTRDWDrzjSh8UQ1OOL3CQmzAExEKZnGD3kvC6bv0uwWYeZQIZiGq5V3hXXrI9mUGC47mhFF0rzikMOq6V2tKxlakPcrWx4LHQCq5mWFB7YpM27SZITxTC9XrUc2hpXBjfBWVTmMLPqfRnfbWx8UmY9SF+RL7U+oR5iZAQfmOjVjpipIA4QNm00PPOcbW4Eqn/BYhChoN6R+uost07asj5cZg40WVwrEWi2gPLkZQGOpjSH2Mq/4zVOLLhXzUXW9FGrC2OyRFLY9Nc4CHYIyDmiXpc8sZzUoj8HnQs4xJkPovt1LtgqLUqrjQPfR7RPOwYOgM1ocvI094UWJ5iwm/s2YavgIzfCTYFVORVODWC7JZxrUGM2GRCvaoKdMqNuZEZl4FeAoQqbJ8wAQf9M05kdyXOaMkECgG/mLKsGq8JeD6na3VQNgQvaAH9NbSZFJzWrvrBwgg2YuXZcA9wVSKsArFXI1jXfge8iqqb11tnOdrZtFi6HoxAk0EtE/zKtwRZ+ldVOFB/jcIMFmfFXXTo/CRMKZGCecVnMZyranf6UOBCwgoXShuOaVDWJG6l/pINObo/7xIxiqlq9LIYGiCVjooXEU+jDgBH8M76TzeEadEn8mcLv4cbv5MFaAzngl5LKSnJBCv2qD3llyvAdZFwYeGJQpSnNaYlcM4EEUJKR8paw5Yk1lKbVKOmTc57znFthbWo2NhXbzeZUVsVOPoRWUotyUNAeCAsmRzhD1Z74oNfO8wgkrgD3h7A5hGKstLAOyFALSgKo7wdopl6Wa9NnzMk1aU5rQx6vj8MA/EFuF5ehIvw71V+4RcvCipFmEwZLvE3Tj/WgPsHRk7lmh+iHWCFDyochsNwgm6Az7cKwUZIkGeC1KI9qGTOa/hTPs6GcJuexa5J0xp22LL7GphoROvKbxndkEoY2r+XLqc0sdaz3L9iMlcgWFVacA/IiVJogrsUD4DhvnmfQ7xlnnLFtNJPWZBUTjmcJm+vM9xtdCy1lWYD+MbLj7IptwpZJVxYMacQs4SfkxhndIb0Im2V6O8G+nVXjmKCjLfAJaPSNuD7NloshW0HIgfc4bZnFI69HVN0qNWxFoClsyXLI6+InESkmEJaz4y2d+KzPmGCugQyvAQIDmuNwowTysClsQ/2Gd0LY+E4OD1aPQyFbVyuiOSXYggSBz7rNjCadBlOgw22tgZuksKkdSKMA3i3Dvp13EFsdTOtCEw0DQqNBCFwc7e2122KVReG+bAfF62CJ+J5ojsSGcqZDKwpNM5o4m4c2YQnAYjAqNBnCxLoi6GkyxS7FBrlW/B/+DvS+CrLft05h4yfaH5DaVltco5ZPmAwtTrCF37aNz1YpMNCEyDHyYYbfnkIjDz4cU4sDrA+1k5XtrRxgbVuPRsbngrLjNGaETl8tB+JS94iLAKRASg50vNVFKdNCQ2mdyiWrKSQPBVaASI6aTOeEasKds+qhwKIQFNgmHu1YO3EmP26nzWjSz+18xBqDVmApsiiGNSbnDJrBIduWiM8NxMcgoQ6/ysSwfoPRBieQnCiOIhkDoYCdLDpusRMEMj3ZmiyQdmhRJIVR56h5q8G4F64dbQb4iJ8G4RPhSMZvhRRa7eAVpqQAJURS2b5SjMhzUnWOlhPktYqJnxwArg2KERR7+6Flxyc7f6ZLsY4Age/DD4NOBtDsSMkk1XKI0NQcFEcNbBW8pHmwZI+bzWoaC1p0YjFVjJ6pnPt1RKW1U3mOSDRiIh8JmIrvycFB8Ig2iZLQ2rBUQPYxnZYcai6tOxiisNfv58C1BLKaPWEaMEyICzBbAUjhtrHecAKhc3EAOMiMeBSz0zmvsyESQN8p6KMectYX5x/oS3BX2eB3BJBDg4XhsGwTtlSRnD58HzZHPCr9NkN3TAFRyapSUcvmSGthrINaMa34GDwQLEwAJ5PnTfekb+XYyrFytHoNsxpMZx43I3+Eh/VG+BhSwgEh92kBT7ar4F4QMF2GVmnkvL13F7UoHE5MOwRP/V6hG7uMYk1gueTgji3NlqkfP8iAQMjDSMOJeTqt6xa2FuujJXCaRDYJjY0G4iebrC9WaUSZ3E8/sTJxhzoxVTp4Xmetm7ARtkKX5Y81KGmxn33MalO1qiyCgQLYIeYREqhjw3O4Cj4n7gEylAppm2bjojlZvAGWgUi22X2jKFQlH4SKHKrHXHf37Ky4WsaU50nO5nZTB7W1JiMvs7mVyNnKoKQW3InGM9WSAMFg4jH9cgLNn0uAQFaQIYDo/PxtiWSEjTeAeCNYJrLNMdpvFT8DDlsu+l5tf7WKScc7lY8cSpet0qLMI2zSyDD5+MBG+dneXrlBhszIHECe5EmETedP3MS0hJEGAQLRFL5d7bm/aS2w1tErYy+3sJ93KJsBEYQAgN3M6+rPmyFBhggiUy4OSeAO2IP+XDAgclSjqDfCRqhL1ASSrKrPIV37zf02ewT4suxo/F5oZSgcLZ/UKIUNuSGIJMe+TdgydCZSI21De1JBXP02hc2sPpot29Vn9flenY6yF7XRMn9X3aCxHiYGIgRcUI3IjSfhIRs+I4AoLBTXAcLmByJs4E8Im39kFMoH4RACikL9rcKW/TL2tdvmz5uv/USy5LJV1SZhk+iZJjJghOadFTb8edELZAg88QAz6pfCl8LOgg5bTiZtmgeajVQEE48pL8toKDtK1iYp+wK4OT100xL5uxSpFnZnFCyVDByQnDiaDeHKJt7mdxFAsjeY0QMCBFUqmg3aEFKpsBlp8AFoNnJhUF7UbJlGyRmXtTPPvrDtri+Y5jC7I+XAuyFhy8Y+aDZAcgqEshVHTvRDVjCjB0SjCU6SW6QyBucuKUWWwPEcPttRRx3VQx/ZcqkCo3mC9oVtMxz82mZLDmMK2yy/22iUNKDUqOwmbkIeTht56m3CltgNjA8o4bxRlquUcCAPJ+sB6AHqtoRI7dbqOba/+bvrp6UFytEDpunsGj4kcE73AYkAa5VYm33b9O9hcoPZHmBGVZ2OluGNph8E6STL8Tt5L9JVLSp01lXWtM3B5rtt+r20Umj1uQzwqoZLTej7SVfBlCFdhTwoaNkxHmFDITWFTXtMRQyOP4l48ROFDdqIfhxl+JR1WRu4SGnYvsZZHzsmU3mtVF8t/M5HbReGsNHnjjZqCptDVlROBAqYWWTkAGGTaozzB4aCT5blWTlHXAyFImYn607BsloCtwmaYZ5x2EMFvcs0dlmlcNVWrC3fudLr674kqqBcZNAgZ5AMgTR3m/hYfYcVBLFAKA8QNpO7fDisVTAUK2jkyTvPiN9haVJZhdltFYPMWpBWm8+pJL5Fk/9JuKwdgcbaeuWJH4rU6gEay29Wv3aVWqwiA2km0yzWtq4KZeKkVVj9PPiO8O1gEksx0pTaLYogkjZqmNsm9OFFIEBO3EsCpcCdkkz9IFKeRb2VtjOrObRUn2W03JjQ+V0ZJefJF7ppjQ5PWKei7S2nu3ZbTLhgqOg31ysB1qEul2NrZOuwrClVOylYfo/ClhpMYau95rI3Lu+Hfwf5FEYxFCNLBbKuGCyWGhV4eoPCxhfitx1zzDF9ZXOtaZRKwnO0A4CMmFVFU1pM5cIm5rNTpjVrLIeoOS1T0gKnWymesSFz2ZIheYO1WXJqkUX5acl5q/eQ95HC5WtV2Op05LQkjimgks2icKvY7EaKIFLLC/jbFDYvhNwXggSwK6dNUpzqkkABgaSlqD0dZk3RHeJ9pTO6LgC4RbxMTn91oLNxS5IPbF9VNVL1c1pFxdlsb1kyQx6UKkz52VXIhjC2BOezcIcHYD7Ov73wbGsh3oZ2M3tgg8htwpb+Fot3yimn9B0nravkg/xg/s/z+HWkthS2ykSdav7y9O0UCFxN6NBGuVlgTzBnqSMlhQfLAUgIH4QDBsbI75AIMRVQzmlNAN28RnCVup7aT0GdFShUn7gyg7Mmws/N5jNJe0/zKcZmHUfVfkmRt1UXBeEUDOnPC3uIXvAgeGCdWMNtwlYjLb4YTht8pbOf/exbNtkggQ+lDA6szfYLY1NXpp7KVQLB6YDbiLrWW9Y6AhaSxYHTh19ChoTUHdVQFKFQS4svS20qD2onMSdYAUwGSWco9ZgOShwtKtbNsLN3tqFaFP2vtPCcDWYpoU2t03/LoSS+L4HcmlnIw8BncJjsXaIfn80VHfkNTssBtGptm7DlaedLkEoWlm415rocdsqX0EGRSm02ofbhWrQDYm1+vKgv50m3s3arnXs1kdReoKUQGOpIGQgHlohfgrNLdGXvW7t726zPNg50EKA2A2SdtSOAAtTElGSFfGrbMYilNo2pPm4ViowY1WzV9Kdmy0Ah6y5qFJpWBu1NvbB9SxAs+wHrXsl3pF1YHcd0gFDYsBdBItoQW3ORbb/ABjBXgNKuOjdgmchyTNNNbaacUVi2vzIw4CeHBBNJBRDtEbiXI488ss8LE4lz37gLHCy7eluxzv0T9vPAvbDXm5gkfTwQVsoGEV4wSQp20Qxpsmp2ZWxGVaUDZd1s+lyt6LLlm2ZSfqgmt7bmotCFQussWLeHir2WgUTock7qs9lTt94cpoQujKpGi3sdjiZyDM2EiJTkbI2wls3j5cmdkiAewuY4zZg0ay39TK4bkwB7gTpYBOuwww7rBchDhuYiKud1WgpYkGsTZhvBcLpth+X68OB3XsNhpk6UvDMCznply4shtsUQIF6n0rSCgQxqhvLVQ/y1KvS+Hx+dPRdfU7tbi4Cwod3R6hk4Nhs4+6J+G1JqUJAtn6ySp1kKfo3TSKYI2jyIfbZYSNBy1rzO7C6kz8bN8/f4EgRACBmmz7A9J85Ze5HzVKVZ5eRoizz83YefZS0lAsd3kS+kdQHBRh5QDkK9ryFYpqaX0m+rEWXVXnX219SsiAxdOnMiTBxM79N7tqk39DNkJ6dwD86u0rcgr0WFjPaYTZF2ZEsDTj1SDHMzB5etggJdm7Uk6j3UFqFmBmw8zCag1jEDNJFh07kv+2uIH6agecAELMWQspLIKYWt1vJugi0WrLGkxA0zw4agXdPnHSOb1uxL9dmGNGT1eR2IMVYCmGvrYWUdaWvBnnMv1hAnWxcFZNuFFPBt3cJbfg9/AP0b51eOkp0Sec4EPWX2YC87iY/p9I5NjKmtR9lEb5Iok5D96KOP7ntscA80OsTfsg9aNrbz1OY0GxdWzWZPWR6p3Xi/DWL05xBK18+NIpqnrRSwSrZIrQPlWmYwHXgjTyvpa8YjU3QVrG19T33wPtwQAh3gLpvIWEOcFCMeZBdIebYOzeAG41vgt5F0xxZrFtgM22/yJXZFHOoUvoqsgJotzUatfk//ItsTAENQxENi2HlREkGd9uK9qc2ybachvh2QWAt9MgMH88cKqOZWsLO2sbDNKpaDAAIyosKiG+NGq9FTqDx4Sen2/ymM/p1arxXl1+Cjak4Z3BxWgh4hsDrYGJkgej/11FO38LWZk5SVcP7AMnvH/3nyWUjsNs+xaDTiI0/a6hS+Ch5bpobs4pMtFNJ8ZBTKIuEOUFCL6ec+xIZcrEzB5TxNwWz+DuIBdRmAmQCWPPgdxx9fzJ5vCWzmZBl5+eKVSUzlszCrUK314xSwJDVWguNQUKCgCf3gq2b/kGqBhgTQ6JX3EEljQgmUrHh3jZQNICISAQjlUM+45rwCk7psFqmJbHzs6bejNf8H8EQwWz3OVk00rAg5C+nIyTQZ/MQv4rAQPRFp2nnS7pMIGj+FdIQ6MHXcFwsIuE1qDuAWDUl5GhVo9PoH1KZTEqWNpPdYHyERXQ/RdQFxeprZBBDtyDqSSwS/YlMFoCtbo5XvNGBqaanUbplJGGKtVJckB7MBVtNlCe1lywUPplNyOHDgk7B4h/LGo125dQo5wZ5IFy7pR5AtWXjbkfsZrYrqVaSe8lQ7GdmmLDwPwQ/8DOyMiFrnNbUZ94Fw6bgjcJhZTAUZAjafSBuAGyHArQCoBNj0wXO8hs/K95EPxCwS6fJZ+mxqU9N++jsIuiaZ7yVbAW5p85sKqiZonYBsK7OQjzFWzBAFSqG1aTMHzw6k9lbW0nGPgPzMrcJfG0IJmhBCpj7oc4YwaR7SJ2GTOKlgUGg3nEjnYWYX8VU1rEteWc4011QIIwAtwKfikKChECScdMf0aAboQMnGc2Lxn/DrcAnAw7gXNzthhBYXzs3mGuB7kYng+zErfK8mM/OI/p+fBCtoOzQkgDoZDe7DNll1dqmBgRq9mtRKx581TXCI98eDg0SrVfxTTaZjjtTc3B8WREhnyJLN9JFINGNGDBIM/dk0gF5HGXIy2SS0Ss48SgR/VWzUejpzzikaBxxNQJpr9LrTrJlEBgMDL+Rv8Js8MLlYObWl5Yuad0zgGKGjlI0ILucb5KhHA5WznvWs/U8wLLQbUJLctMTOFDT9sQwYMgBYpJNS5rZzTAFdJjGhWADXTC3NA2VDYEBmgUOiK9WCVUan6/I7i4+/Yh5QTMnQ3wEM+B0Alk62yyrqdOZX3eUnizUw+9RQYAJV72o2w3QxQ4QOGISUEgsKT4uDwmdkt8gKrNrzLafhGbTgRphsZ6NYOxxmpicj0E7e47sxnU6c4UGgRWRPpoE8rVOpWxFijttMGGOIgzePsGXOFOHBYmG5EvC2IJmfkDU4JCAX2R2ztd8zN5UvhUvOQji4Sy2hg6h24wQQ/WWv2+SyD2mnRSqYWsO8UOGwNWCJinflDCsFUGo7pg4/C3gEAbLxcgu997q5r2TEphBo2nKatO0KOIisocFIZhnwh9hQAF+wTfxE8qhDxShDhM5FeXEZwftA2AkMwAPRaO53VlCxvrgAXvMQ4D5Z2Lg5/AhOHNpLdqZOIovHKeUCZGiyeVnmV/NsyzavS2ZCzt7keTQUG6tP6eIISBtpMiOeQ+TY7+SbJbCaEV09MLXKPFNI/J1+l4W9dtk2OGCjNKeYezQEjBEiOn2fFiGyZSJbJXvzMnxz78luANCaN87eua6l8BBBEXueGrj1XTOFjZNK7pNxzNBnZIDoh2QVFs/j5BLFOdNqlcLWQtOTScpPVD8Jdtgbmk6nK+tzAOfgxBNp2b+ipnqSxl1ZGrn5HsiEXPyb5INhXjGPYGpgdBIcWEOgEtYRJ5vDSpSrNUg3IQOB1ljsRQtlMpBjLWzSTFrPASA50dAMCRE33DX2O1u0DpFoJ2k2BAfQlqkunMAcyCqeZIoH7Ub0orOYPtvY6O2pTNWh+tMMSqRIsXloEkFUfqevGAtJrtSets5YqqmiFiNGbZp52iwU8X6TouNzfBcaDmyOw0AE7GRiMjVYD3xO/T7nihoA1JrOjJYXxSxTQPwdsgLXqE8prpoZEA4IsBLamsBqqDvCXAGC7d+5ECIl/AptuAGC4a8sB6Qd6rT8LaQ+yX2LClvr+hQ8faWsAoJHRiRNS3rYCGwmw3jBy/K9Q/UTmRJr1S+0Wo8m7Qchcbq0WgOzzWZC1yGCI18L2ZAgArNugGLxEX+TgHVq1XmFrTXPIbWn+B7ANdw+zLyEA9wnUQhTeOwzCAQHN4OpIU07E2IQ0+F3FgPAky9Dw5lZyLwpF8XFGZkmHXkVTZaHKDBJvxZ/AwYBJ0LN0y6C4IED4LAQF1r4pDVHdKxAOfn5tVhG6MA8p1rKVKAsFDYLQJjDgTXINFWuW2qf9N+mmtF6H9kg2gOE+cSEY8EggDqV0Tnw1g4Dd7D/RKpkmZJ2P0QFGzWjeerdSC6ETAE+h7lAoyphBRPOmAn8Ik5qot6169Es3v2iHRRbjxrV1Y6Zq2AYt9JHCQon8l+Lm3XWFdJqNjONNVYc1ALRExmo8+7dX4IrUnIEKgRSspLBIrP/GkKIP0dmIe+l+reThK0WqXoCEBxnMOH/EKWoUhE2sTiccbQeiLzjesaCgiHtMaZV5hW2ZDZM3bRFApchFF9+XU2KVwytNnip6aip9RlDE1pq630eaHr8csYSwMRFq+kW2RkBoTP9xt4CL+EO6CJVt2Iy9FGLZ3WM+R31j0kiFeMIQMcAWl1jlIrTi0pmRGM2oUk60ix2yBTMqJa21f+3SIet8sFFzXuFY/LzalpNMDi1XtV4Ceu0KPFT21C03I3WtEP4argbxx9//BYT2yyBrUudgYqLZASKS4ICSpZH9WknCVslJKrhuHlsOyE8aQoETogBW27+lBPBhUPBweHMKcA19dOq4czoborWmdUTpCV4qSmWhRCyyKZF57FcUOA4fb2McBVWzWlti7BIC4r6npypxXewNwR/CBF7KEyEEkniBc8DPtsNIf3Siv+11nPyBOP6f6I68n5cgMiyLFQJlgoe5pTolJPtxur4tibaZRCxjhGHy3brTq1WzV+Cv2qqWllf+9saJEwVtinkhXRj8sBT3MTesJdQr9hDHgZ6pti0VkBHptNqg+da+V9dp8kXXC+eKARWJlhL1hHK18+CEDQg8yfBmHRGPeUVVMz5UctWaq1rUFsr6KgsjKpFa8ncUOvROtR3kfyxabSMYH2NCJ2CawDabCKUNCL2Ez4gE6cBnVEamE9do4RPqo84txmtPCqlGDAPKMQLtayNCyR48HTwf1ghpD8I8bOKvrZq2gszC1oQRKuAuPYxqRFx9etagca85r0VxVc6udrNjkQEe7KYZWLjq9lrTcsF1IEWTDgrTeYsVvakfmYmldO0mRqi/sC0hvRqbL2Mzpz+AQUafhz4V1XxQyH8OoZxjJnT1utDflZti1DZsskcaXVXWkWzwBoN6rJUS8EeUJxtu1IJnlop6VfsI8+TkCdaBZROxnQSD5aKRjMdU8FYFgtVis3ndECLNjrlIp1erFqWUgOSD62aixZIrdU+tXPOokI3No9zXp9tSNha5rIWEacmrDShRYRtrD1ZtpvIz8gx43DtiCYRIGAO87Q5sQVhg43Ca+Cq0LDQhJU0mv1LRC3mFrZWI73cPFUpNwGWRirIohHrKS2KMHjArHIDcMigIqEZsz5R8+oiVRLjbo7yaU1GaVUstdqFpoBW3tmYsE+Fe2rUmVBE5qP5Tjh2kDopwbS6DKuE0Enm1JyiNOD8gasiaPhqRqAelNrpaKy6f9JG1GGr6VvIfSLlgjk1tSEFxdAZn4DkLRoOOAQqDXidAudpT8jDEv7dnneV/eRawjQmbEkmrGBua9DcVN+1ZgnSAlSNaLABLsacCwTNCNM0o0NVpDzpp8HigQAqcmDQUnl1rRLLuaGPilG1/BdPDHgag2+dzKag2XxEP47/I3BEQUAoMjAyJM9O162ijzHe1KoizRa6Xx37sUKTmrCv9O0qbK1gYcjxrn15hR+qq+NnO1CFIiA4auwFWGidrGcRE74brBToWuxtct8q5y//n1ptIWEbEr4UOLQQN4T/ho331HBDzjjClGpauTFUNBkGIhyAYiNdNzYrvYaKaqupWDbAGCqHy2Lg9F+nCptuRw0oxqK3CkK32k3kOmU9Qn4nTjyHGi3FfghtiBRIpND94Xf28IQTTujNZwpQpczP81h6slueOm6MtAeMDzlv4jWSGGX5mgKh+BfulFQVT0fND1ZHvLIXkmO2yIjslk9WMa/azyyzAK258AlIV2FLetBYNmVqWsrPQrBw2r0mGCbQu6np5HDjzthhyajTPKiCB4mCPSExL5EiaeN+344LW6vFZrJanRJD1oBggPQHQmYzwTSvEvKIZPHhIDWi4aTY8FlDtZE1yZ3Ulqm+Tqr+IX+shZ+lwA/VA1Q/VxOUn1ddk5YpnxLQ5HMeOn5Sw8nMArIDYKFpVbKXiZCHLcIgv0JNT8qQQleDkR0TtjG4QI3ChQGHIHDw/O11xqkxlOZmUeeWtCGQ3DBqHg1ng0HYCNkDoxIUzTMOQQRDLJKxZsdDI5BaQpTC2io+qb1us+h4EQwtfcTc+DSpcg9ZO9vVss5oNNAAW3hlB82saofICVtYJCDdgJavNo/LsrIGydm2gQtCYAixESBrDLlJUyLcvD29dFIRRiJa0mD4CrUlZ6sHW6vt/BBBs6L/Q01ZqnkbasaXQlU5YrUaqqXBZm3W0D1kvazWJSEkaPEUocBQJkdtizM1mgFARqK8B2sEqsDeZQBTBXtROVmJsLmgMhXcdFBqohmStwiSbaRsOWUHQ240Z9FTgU/tJ+2kOKGanyG2yFBOcGizkshYm7W0nPehycNpWqcI26pYyQnUerjN6IB50jMPCphRpm2trMRnvdFsEiRh3ZJ2RBPyGfIPc+DGGHVorcJWq7VzMbD1ZAy4ec0mD24WwULbYVI5ZQgiJpXfcVJpLAfDAHwoUyGp4isfbIrjmn+TecMUupYv18p7VnPZErZ5NmnKJJdMfWlZWCO0EtE9gYDtEqzEF7S17JI15nWeY28E2Vu1Cnk/yxAjVj7Moi4yTj41hVCIGcCGA2paRJNqQz1L2+z9RqSKc0vDEvhTpLgyGmwtwJTEdaLdrXmb1ZEfe7RMZSVpzhu5tfA0rlWmTNaHEMGDAKDNKBJHqKxWzyaOQhrZjhVuGgU3tJ5A0DyEFmwLstcygV0TthalJNsiqBXwI8ivYVIBdFXh+guG3Zb4CzDyf3J44HfgcVRGJYMBYR6aezoLKshkeprRDBiG6EKZAqrFJ3VyzSIwgZ+R/1cApOhTaU+0CdRETa9dzn1kNZR1vkJSvBc4BKtD1KoQG5B5EGuec9fNaHKa0rG0HE1fC/8LgSPLIJtASlI2W8Gssih0GTKRj0ASbOBXWCLoBlRhmIfwWMmOrSKTVoftbAPaGrG4jL+WhEQ7GeXrPA+9S3+Y9ZIlbc0A1sG0oZ3ebdfFWhKlAvQCxKdw2xwHYbbaa1WcwpUPU63jBn3dyno0HKcRbhTESyPT7PgoTUkGgpgQQQYNWujRQU2o3LgWYWAMXkhTlymkofTUWO6zDqho9eWYl5OW91JHZlMeSQUUawCZUezSACvHMdobzpJLXqNyCko/ZZkKUxIhELYsj1xVU6CVCVvLx6jcN08N78XPwPEHyKWCPpskWw6YXYcUQHlXhPO0UCC8B5dDgNF2KThTJwNml+3K6Gi1oRpi59ZDNlXYhiLmBGnxVTGZOPFU+gNp4PtiCQgEdEeMNu1UYLsE1xZBO+6447a6hGbzoMzf1jK/ZWs0diRAmMUpM++pz3H66af3i0ceTtzNTIMM0drxR6FjkVlAOgNRFYTwWn0+VIySk/SykYq1EQqfJ7z2htW0SRrERfCeEiapgtgypXkoWyOONNNoH6JMhIRuBBw8ICMEiWDAOVJ2cbfRjykpsUyS6pAl8XlXNVR344StJqv1k9hMFhKzgJOKP4aZlE+lCbVTTs4V0ExYOIt25LSzIZhXEHBMdlKU6sx0AwMHpNV6CM2xAmPOUWZq7WDUSp2lRkxBrTUdNQhAk5EuAtxmGBuZGO5RuMiySTW9a+KcCgvIeR0BZG1p9wDumde/7vqOtXxJsnDFyYx62EAoLDBHwdXwQzJvakRl8xoELzsf4vRa1QV1ho2huAahw1zgSGO2xdRsDeo1IfRsLgKHpsrevJmqQXB5XQJhTUZnUJQwSradqOzczLrgqFMQBMePwwdhEU3GAeTe1VA20PYwCpJL4dJ8Eijw99C4WFs+X0hjpyrWNkLYahuCxHN4aJZo78BpBi9C2M5ylrNs+XOCkNY0Wi4ormQ0a7ABRkdzFCAT6iTA6dB2mr7q10nW9Jo4BAqWHYg0rRmJ8rwPmwQOAbkVp0LwuCZayVKbgRbj3gFlEZpDDz10iwOo3yrvTMhIti0FRty/kAdZGD6Tz9fvSrdgJ7iAGyFsrf4d3KyaRB+C30lR0Q2SLuUUY9gtMk91jutJX046k6MJcaIpsiHfChUdM8tUFSIxNB7+i8TNxMRaPdkqpyxbZbUKczO7YWNAtAtCT/kcfVBOOumk/j4BVjkY+K7yzSwS0l9lDRQmW7cKGwlpcL+s2bHHHtvnpelEwKHxMCfPbQibPCh8tmSsCikYBeYps18avhyZA6JOzGMClZ5wFr+aFiMvNg2tx4bwk9pV2qezqbBVIQaCnAPDgMBjwoj4yHaQiEYIMa/4lfwEdrAnhlqMB8/xGtfM+/g7hAr/iM2mHwY+JFEzfhN1lwgDB4DrkVyqa5A9i/XRvN9MnGddJ38PUA52Rk6Z6NyDkNQgsVC197q129qFzRuu5V+VdcFGsvH4MPhg4GuYTYSLSNSFxgEWtFTL8T60BOAx5oQ0GVNe+D/P4wchmA68IEOBrweizuQ5TDmaB78PLYtAUsZG31gcd6JoNDCCxE8iYQiKQBNgYLQyoEUBRUA45wQvwA58F9frhBlLHWuyXAEy1WTaySG7RplGpNwj38c1Qu/yAHMQ8EU1ow48W0ch0a6a0SFMLk+dEWHytlgsNAObD3sUM8Giyy7VfPJ/tBhakDCf96E9SDIjTAgaG04AwnwEPsNWXwgBADMONcKB0NGUGCFhI/mJhiVPCw2HB++D+0VpIq8hrLwPzcl3Yr7xGzFtaC+LSASxFSIdfYVM31NN7t9kWSTvQ5Ph39FNCJOJJUCjZi9g1zTHc+bo7oMyGh0DVTOfWudg5oLwXoQOPwf/C02HRsuQH62BMJEnRNgQOjYcQUKgEDKEzteMbBE8XodpgsCB3SG05hQV5pxxpRmXWWG06EN2iwUk2YvWSFtYxwJvH3YMEpD1YPHTASFEmYw0wgfEjCeUUhm1tVdbzjw46IUtkfrUZjU61Lcwt2phDY49pg36MmaRDcDMoEXQKmgjTr74k925eR8aB2FD6BBOtCGCxt+hCenkg9BhntQmOeJQgdAMyuX3oTBmCimDF6GJnFsqEUGBSg1HzpPfuTfuC01GaR0+Ya20F9qpvlgVtlVM29kTwtaaA1/HTCfAmdGTyD/P09iGqI7yQdJWpL6YGYVJQ+shYGqHHO9IvQPCxkMMCw2JBqSfHLCDraKsEPORoyLVSK3ht+mLcR06/5l68zMUSuc2WNyNb4bAcwgw62h08DKiaIKRZIBoFXwuC2VatKvd6qeyq81ZarfvVjV1vlehq6VlRIw47jjnTEpG6BAkm6QoOGgVOFxHHHFE78dhXk34qwEz8kvtJPyQE+l05H3ol+VIawU1P0sYQxOsabWvHQKP5uUAEWwQyeL4Z18ND2yrVVULptmEZj0b2SloVlNC0XnnaZqnBMAkG4HGI6qkUzimB4jBfrBoMcwmWgwzag+yhFVSOFIrtR5qKDVYTkIRokjzyvcQTTsqEpCav0ezopXB3RjNA3eP++HhVOjKsBkDjzexE9TGCNKUsY8KWnLmctaomtGJKo5lBHsi/UNgAdeeqJIo0ql5BgI5wSS1Tjr1qeXM4ypM+bzBQQovAq+wE4gQvRLZImBoMMwkQRA+KVG4FPvaAqO2Odgrj43SXkM1kWlGs0FeVqpXBD/nnuLjwH0jVwoWBY524okn9hEd8AEBAeYV0ytMIW1dITJQQHOlptPZz4fJcD6LoIQSObQrwQdwCfgbDAyEi0OBcHGNpsfGqvxrMc+ijWkOOmEb63U2pfA2ay5lTSRV2ROem5S5zGxpJXLO80AFoP1UfJOXZNNpuY8AQrFG0+CUw4LFDNPIELgBWMWx3fwObof/J5YH5IK/yN/yGWQp0FjUX9Bng+/iO8ks4IOhgbmeBLRz6l9tHFOpQa1128ROnXvCZ8u6xfTX8rlaxJws1xa7oTJxpT/DwyfNg6YhfYVTDsRAiglAGSYGQgOtnQfakQfUbMd5A8cgVGQTyCrwWQgWkTNpLPOUQw0QPUC1pmFWR8d9M7oiLZiCpd9WBbD6LznaOyOy5LHVpsar2Mgpra4qk3csUq9dkjZZa+2ZAGGsjXxt4lJrDLJlqJuTEWtqhzpbYKgzUAsArZTx7C2cxS6zuhqNzcpqNbmpRMy9rN02piHyUF+N1E517KH9YrOGICeptMYXtSq8a9PDWUM4WvWx+ZmtNvVDglKFsPa9azWB3he2FQlbS4tksr52v2zVbNYClCk52taU4jq4dqpWyeufZxTSrGtbduzRbj/+BwZ5jZGOH63xAAAAAElFTkSuQmCC', ship: 'image://data:image/jpg;base64,iVBORw0KGgoAAAANSUhEUgAAAJ0AAACbCAYAAAB4f5nLAABIHElEQVR42u3d5bNkX1K24d+fAcEXIBjc3d1lcHd3d4fB3QZ3BmdwdxiYwd3d3d2j3rgq4u7IXr2rTp3Tp6tP9zsfdpTX3nutXClPPpnrkd1u98hNO/73f/939z//8z+7//7v/97913/9187r+fn//d//7S77f/7rP/7jP3b/9m//tn/uP/z3+r++2/d97jeOrevoN6617/7nf/7nrf9fr9Vzn/lO/+t11+g/+mzr2vqt822NwWXH5X4dN+6CmngD6/D82GAmJL4zf2uCEpz5+97fOs96NLlb55iv13PP/5xCT2Bcj+d95nvzXub/zDHpHvz2X/7lX/ZHAvugHTdO4OYxP1uFsMnZEsgpeGmivpsgOdIqUxjSWP/6r/+6++d//ufd3//93+/+5m/+ZveXf/mXuz//8z/f/emf/unuj/7oj/bHn/zJn+z+4i/+YvdXf/VXu7/927/d/d3f/d3++//4j/+4/73/mdqw/0/o5vV0f4fGZT6nrdPYpyzMJwvdFc0twfj3f//3W6anAZ9CtCWsCazfOqbZmtqDkBCaP/uzP9v99m//9u4XfuEXdj/1Uz+1++Ef/uHd93//9+++67u+a/ft3/7tu2/5lm/ZfeM3fuP++OZv/ubdt33bt+0/+8Ef/MHdE5/4xN3P//zP739PSP/pn/5pLxyZREf30eG8CX1C5379jtC733lP08R77j+OmdwnC91d+HdbZuvQd6cWme+ZQFqJUPzsz/7s7kd+5Ed23/RN37R73OMet/vsz/7s3Sd/8ifvPuqjPmr3gR/4gbt3f/d3373jO77j7m3f9m13b/mWb7l7szd7s92bvMmb7N7ojd5o94Zv+Ib7R6/f+q3fevc2b/M2u7d7u7fbH37jtx/wAR+w+/AP//DdZ33WZ+2++Iu/ePf4xz9+933f9327n/iJn9j92q/92l64acR8wBbSqtnnIklbTleBcOYbPiha70Ze1OonHQsOpsbreU63CWEa/+AP/mD3K7/yK7snPelJe231ZV/2ZbtP/dRP3X3ER3zE7t3e7d12b/EWb7F7jdd4jd0rvMIr7F7qpV5q98Iv/MK7533e590993M/9+45nuM5ds/2bM+2e9Znfdbbjmd/9mffPddzPdf+8Tmf8zn3z33/eZ7neXbP//zPv/+PF3/xF9//p/9+0zd90927vMu77D7swz5s9zmf8zl7jfmjP/qje+H/9V//9b25dq0JURps1cpp/TT+1PoJ7+o3PlnoTgwkjpnMIk8TtPWZSUnYnvCEJ+y+4iu+YvehH/qhu7d6q7faveZrvubuFV/xFXcv/dIvvXuRF3mRvaAQomd+5mfeCxBhe4EXeIG90LzYi73Y/juee3zRF33R/XsdL/ESL3Hba5/77gu90AvtXvAFX3D/6P8TzoSVUDr/q7zKq+ze/M3ffK9Zv/ALv3D3Qz/0Q7vf/d3f3fuFCdyMcBO6It+p2WawkkDeVJN7YwVuDvKEI9aIMDPK//njP/7jvS/2nd/5nXtz+SEf8iH7SX3t137tvaC9zMu8zF4wCISJJwyELO2UYBG653u+59u/57teJ0SEan0vIZtH7zt81znShv7b+871ki/5knvhe/3Xf/3d27/92+814ed//ufv/URaULDi3ibsM6PvFVJZIZ4ZmV8kgId84ode082BzGwWrU3T4WCCOOy/9Vu/tXfiOff8MpP3Sq/0SnshesZnfMa9ecwEErIELcEx+WmthIpg+I7X80jgCKSj/1k/J1TOP7Wg1wmo73S4NhrQf/kuc8wv/KRP+qS9Gf6xH/ux24KTCQO1KEEoU/NnbqfPd6pA3WvBuxGCtmJV03kW3a0ONo0Hovid3/md3Td8wzfs/TNO/Mu+7MvufTCC5tHk8qmYMs8znWkgQkK4mnxClAAlJPyyjmluO7w/TbDXtFdCPIU07dk15DvOa+p73vN/Fs87vdM77b7gC75gv7DSfBYcgfKYLzctwRy/otuJUT7ZvI5jRmH5NZkSg8yECgi+/Mu/fPeYxzxmH1XSDCbaZBE2h8lMMExmE55f1mdpoTnhHgskMonzmEGD7+WzeSyI6P9W09xnmfAE13WkOdOizuGRAPNF3/md33n3CZ/wCftIGDQjAg6vM1ZZgxbuhIk6DmGBT4ZMNnA0mu2Xf/mX9wP+0R/90bs3fuM33msCpsnkmMSc++m3pbma5MxmZnFqOQLkc7/13/l4aS8ak19Io77cy73c/phaLY3n/xLa1c/bErxMrmvyOl/PeV2XRSQIIdTOD6L5jM/4jN13fMd37H7zN39zjy/mv21Frr2/ZjnW75wr4r2vkMi84emL5MMViYlC+Tbv+77vuw8I8pVmpOjIxDWx+VCZygTL5KWVTGgC6Dsgk1d7tVfbY3GgFL7Ve73Xe+3e7/3ebx9lfvAHf/A+QOl4//d//937vM/73ML1RMhv8AZvsHv0ox+9N+2EyMIQHTP7z/Isz7J/nUbteldN2/0kzN1LC8YCeJ3XeZ3dx3/8x+++53u+Z+/vFSyk9cqIzLTaHN+Z952/eah8upm33IpSJzwAOIVfwdU+7dM+bW9aXvd1X3evATJvU6BWJz+tlrbrOe3x8i//8nvB8n+Cjvd+7/fem2rnAV18zdd8zT7T8L3f+717GAOexp/6yZ/8yX2WwuG5A9gLlvmBH/iB/fe/+7u/e5+pADiLQvmbNLMFw+8EKr/6q7/6XlsSqDSiI02bn5ewpXHdI4EL2nEvzC6fTwBlrH7v937vNnxv+n3GmI8HkhF4rBkf760+9AMtdGsyfs0WUP9u2ACJ0MAFX/RFX7SHPAy4gTZJJouwGXSP+UMJXf5QwlYESlhf+ZVfeZ9FeI/3eI995kG24Fu/9Vv3gvWLv/iLe43613/91/vBn+DrRXjXatZKyjN7hOBXf/VX90JLkAm1TIVMBoFhot1D5nZdMARuRsRpxTQ57WkR+p/3fM/33EfwIl3nNo4FHWkyrydZoPEv0vXdSXR44IVuRlAzWKDVDIabNkkiUiZLgBDAyiQRoClo+T8d00/yXb/zXcHGx33cx+3/1+QTgj/8wz/c+4n/8A//sJ+Emf9cqVUz67HiXisrJUxxza+6P/cpDSfqpiWlxb7kS75krwmZciYzYXN/XhOu3AL3Z/E4CKIxSQBbZDT4B33QB+2xSuSESW5wfveaMOW+dH+NwYRj7sZtuq9CN0Hf4BCT0CSaFFHpj//4j+8+/dM/fW8uXu/1Xu9WJJcQGfj8nQnQet8EeOSTvdZrvdb+Pz7yIz9y97mf+7l7c/czP/Mze0GjAVrNK5VoZbGsQjWFayUbHHIjgiumVrS4mLjywMw1n/Wxj33s3m8kgIRH0DD9uDDF/LxMcdov8+x3fEwR/s/93M/tF5Yxdjh/QHtCNs3wVBAPtKab/lsmK/zIYfD5QlaowS44SMCKIJsA5oTAeW9GoAZbcp5zzZTJtxpwg7xy5CaKH8a1ars1Fbd1XJQ7LqG/RUSdgtzCAwd96Zd+6V7TW3jcCQKW6S3CLZjK1+tzYyNY8Zl8L4AZuIyC1f0GJM+56b11jG600J0yKZPI6DPq/jd+4zd2X/u1X7tPvBMi0EBBQqYkCCSNR6sZWP6M96W5RJF8QMwR5ovpLHpbCZ9zNWcS15zlRfnfi0gKPb+IjLoC37SNvDEohCvweZ/3efvomT8aDll2pTxugpdpnouV9nvXd33X3dd//dfvhTrN1j13XkI3gebL3PuNELq5gufg5qAXKTErcqRC/yCBsC0DWPrK+8xmuJVVDY6Qr5TI55yLHkW7Jiw/pYg4bbMCo1PjrbSo+dmxwZ/3e8jvO0RvL4OwCmtAOFdAgCMPy00A24i4jYPxmfhkkJCxK7AicATTWAme+I/MrQU57y/L04JrIazCdyPN6zGhmwdVT+V/7Md+7N4kPt3TPd1+AEVggbszkiuP2Sq26sEcKEJ8NamhVauFyGc2q48IoT/FZznVlF5G6NagqmBjK9U3mSa0lCgbrAN6AbsYu3K3LABhNH4zs+E7aUbEAppTINVCnGTQFugkk94LjXfPcLjJcSsy9VrqRlhv5VmRJbn5LqK1Bs1AETSvDRhw1fcMuDwkLYk+zkQ3SJNlMdm0xwbuEG54VcjgKhMzF+iKV8ZqLvoF62Ayi8bBPxZkKbgyJ1mNmYnxnrEWZAG4+dCi23kec5Q1OiR01yF4167hprB1QwTAoP3+7//+Po1FSxGwAFHPDY6BCwydAYTVCuWHb/n9L/3SL+1NxMqs3RKSYwJ1rN7iXDSfLUFdhbCxbBxpdgEHEJvJlRLkfuTvlvor4i/a5w8acxqP4BFec1KgFdQTVy8X5bo13j0TuKLUUi7giq/7uq/b5w2tRgGDgSFwBKsBmQwOPh1NJyKl3USjcxUmcPklDd4aMU8M6m5hgMsO/jEe20XadEaSRZ7TDNNKEv/ysPxiGo1FIHil0PLxaD5jWcrPmIuQaTxCPC3DFgZ5o4SuQWiVZOqg4aVUsGGtSvgTp3YCuVYiH81zZsJg5aN4n3bjSDMrVnlmYKZ6Zs3oMSbFGk0eqitdyxbvhc87BemUOtYVWO85SAjWp9ZDXQYtxmLknmRRjK/xtODL1HBp3uEd3mEPJBO8cMUt/3Je11zcW1p6636aI8e1JOzz25qwyu8IHr9BuO7m1tSOwcmnS7sRQubU9z/lUz5ln/fkRFdZNQuOt4RmTV0dqkk9FEisabqrZl5O/e3UhFtR9JZ2nYssjM0YGatP/MRP3PttBWKNa8HZZDJ7jq/HvwZOm6uZ1pvnLp22FqKvvvMEzbci9isJXaYsMmAX0OcujIPvkb+AASF/+gzP8Ay7Z3qmZ7qVwgkOMTBFpw2UJLyUlaCjxHQwy8xxrhHyvLlTJ/4QaHusDvWi8TmmvU7pRHAR0XLWQ8hsWJBF7HLWkv/MbXhnAZo5KKgoi2E+mGR+NsKC3PPE7xoD71fP63OPBR4hAl37ev3rmF4pu7C2PUgQO3EhvoIYFCGrLOEqYDAgsSdKb4FM1AjwM4DGBrOLjyk7/Y7ZmmHVFodueitPmq93XX7LoaDkIgB9+lGn5rEn89r7zC1gmf/MZ2M1SplZ9MZ6pc1zazBvAPSgLAJWSswjwTIXHhPyaPMhE83FsRYcV/bpVru/VipZAbhd8p3UdhotClIrrZRWYC/hBPQCefmAVtX0GbY016yK2jJvM3G94mdrQv8660ZPFbjpFx0yR9NP3QLg03hrkMEHDimwmEMGpqmdLJzy1soyFZizMsE1/L2UCaEj2BULhX12JIDHrMSVmSKrAMwAAmCLPyZCsroIWjhc7I8S9KJW3+OLiMSmj+CGtyZy9gE55rCu2viYMK0wyt3WfJwKPG+9Dqw1sQVkW9mLlfk7AWX3DoTXeYDgIb/y3yZZIvJAWF6M5Y/5mI/ZV9XRbGGDAeyZ1SxM50zgoqcdcxEuPZhrH465utwo/IjGcpNRvyteiRVhRcUOwSnDbUP1mStmnYzJfE2YDvlj07fYgnHmPdwtJHIsQj4li7EV0c4ahyb4kEZeOwNEMjD5BBaeifyAcROYHHO5SjXzkdZjeVgdSoBPTnCZ24ifk+o1sz1d6xTIQwvvUgM6I6a11ZbnuHDoOYXlBIsDWw5w1g94LsCArAN75Rmj/ax1rSueNU37VvrpkDBNSGQ2rjn2m+uOXrc6S11k1vvPNMpW1dckkiZ0kTWZSr4afxmNPv+aMoiLNwM58yfHC4Yxp2lNWm8GSbP4Z1anXavQNQBrIOHPCQ1KjhoBUVI+RJgRQStFY5UBh/G9YoOkumdUvPopW9cx0185u62+/udQtiJfqAjsumlcK7tmi3Sw1UNvrepfr7+JXWtf5++6d4Lisxg9MhGCi1n3y++O/j6p/eYSs7oxmqWPqyKKrHpt5nX1PTpxGQf4jmQ0CraVQ7t1A/yEUjMxfJlURS2oOxPfW6vXV6xqJvEzl5xafUAksa1mEI3o1+GanANTo2LlhHKr5rb7Wv3HU2hNl7UWzuXacQlla1S6IbFKTbl2gHjdoPi6vkNw1gKmaeJSBqvf1/eYSNQvGq/WFmUtKoeMYNGj2hFj6LeRJlz3FpmivnnX6tOlXeafEhrRDj5bgUNCF0YUQEn4oOIEDp5EWPu/SavZ8tWmiUlj+J3E/1d/9VfvfRDXIOwHFUDnnUc0hsiIayeaM+gmEecuRu2W8BzTSqdmDlbumnuNK8f3RVcHnNfQhzDIpQrC3AMenUdsHBCIbk8EL63u+rcY0Kv5Nk6Tsm6+dKMS1U5lQAAFeeW8WSykWtdlUTde+XcFPAkcWQhCOQabXCq57aLd7DRFNAiKEeGq4JnpnEnn0l5UOHYwELIodbKIJ7C6lfyehxunwQgXmo/zInWiSTk/Aa/0z2ufG0jVWEyM9l0//dM/fcuXTJNOtP8qrTBmy9qVoexc+GzcChEljV9e1LW6fofrZfIsYNfvc/ln1WUWmcm/KGe7ts7t0fsgEALPMlX6KJgghGUqPPfo/IJCRFuBRV0DyhAVsYblnSR0c3VcFP5Xz5Bg8McMoBZYrRCCVtAQRcnFAx+tLuaPSZmrc+Zst1qfrtkHjyYP8v6qr/qqtxVKg2BKr0XtLqAhdAYTdGAFq6NQEUb7MdFzMlsQaeFT01ozjZbLAHKQ3xSlEx5OuhxpxUVrHUgYmueEz/j5PiGhEfVuydqsLdIO9bLL/61HH41Hw8qHzzEqVRa7JxyPxnUPCVX09jVynU0gD5rXLZM2J3imQmarByenaVyMldDER58uGopaY8CsFpmK6WdsOflb7N0ZzfotB9fkOQfN0ODMQuxZhJ22TRNbwT5DmWKWBUG0CA2a6V6rxI7x7WbfuK6VEDNLJlcu2Tg5Zy0p6lkyK/8PNeyJGcK556u6zq3yx0OJ99wT1+e+PBdY0Pgi2rDTOIyxkOtewJpwYfieES+mCZ/HRQv0kUPFKivwOH0qN+mCTRRzNXn5hKyahoiDzAj6jd+US127hx+j/MwozUHDOndptFkpltBF5+aX0LxeG0DHbPNQxT0BZr4ISRHfRS3MZpf2TExwBoiBEPMraVUauAVZl4EKqss9x/zNxyoYc/0Wif8guNKL3JqtDu6HOIRb/ifh4d/yGVkM/18gGCM5S8V1UmvxVV/1Vft7m2nJNYV4ErVpHcytsrkZffFN9NGQmGc2G0QXVv+1VipfT3WWyKwIqBU3hXvCG1P7re+7NqaQEDM9EUHrejR7zKUpMvVpO0KaJp6QgeorNahVyue7bmmTtaxyRm8CJGlAAQEqV77tbKgzyaq5BmnqTO3adsL3ZHa4NEzsIb9z1cpFtvN1zCDkDKlH11pJQMGFOSWI+X0EXusMgjoxu8vmrR/Zctq3oIqpsqW5cPUDFxM0r9MiVZ0zKxDxHPat7kzHuFgl9nvPQBMItKdo2gnbNEVp31I7Cdv8br5LJtoAWySCHYtKpFn0F6SypaU50E1kdHLV9s4dzd556kFnzOpzUoepWmR4DNt0XTXuyV8mdKJ10ffMxx7TblOJrF3lHQRPdC9jkbA7X50GcglcK/TBd+XH5zweKgW4UOhWn2VqvlmNT71zQA3oHKh8qQBG6RQ9PVRp5YxvNaE+lh/tvLNull/IFxEQmJBZkJyZT7h6z+vqROuC5DpFbUXefscc+x7Bk5qzWNIKCd2MsOuA7jmzD8XXUaDaDueq6WLXlal3/gKFyi2LZmuFkcXI52IG4XgWxEoZOrS9wSSlTqGbAQBFwnoIHvLDY6ik6er5x8zCEA/1xNtiPd/h0x1LQE9+lAG2wgQPk05ucBpcF+mimV2sXysiBHuyeifIeRF3bO0wbnLBLuASAlMTmia09mHTpNWBc7ZmTTPnW9UzhbAgQuoFJ0oO2Z+BT9pjElfBECr0u57ZsiyNkU8304HG0PXUVLsyzHrW9X1jKuhB25+pwGP8va1S0AnGlyqzuIDAzGds4xbBhL9co/chB6LgFUyfQd9W+1nHHZuDbLXS76JpGP6OwMDE5JgHKs4+ay5e1dfcwGNdccc2IFkd9hWg5tPwm0SftFXmKfO+Np6ObJA/1XXmE84Gif3GJINULLQQ+Fmjkdk38PxM+F8T5r9dV5M24Zt8uNmLJcbN2p+l/9LXBZECbCEBP3v3nUoYne1gZ9otWAh+F4xSK7V8yaxYLoEuWjJAE2aac7qmM6csPbJuX7S1nVHmEIoOnc7Gz3ZXmVSfGWyAMQT9FGG6qJP6VmaA1uXbiaaYQtFnvg+zQGBqmghkTRMX7RZMTG3iSHP73dM//dPvhVqkXMfzteORR1G5yJe5918eTVDRYFq0CazncYB2/qQxdA+u3T04RL6uAcbHrFr4tOohetehGoXSlzT2BPcnDOZ/Re8YKcEmCf1sNul6QSi0XdVk6zzODlbrcQeoOaGRWU9KlZpgLRxq5pLPka3PrAoeAK4zV3iIPrS16cgWoXHrf9ysnKTIWOEPQf/Mz/zMvaNrxaqKBwdIjYF2AKxdb0LHxCYINZ9xXwkioXQ/MMkChpr/uCZaR6Ckb4jFVhFMwjt7Ga85Tq+Nl2sTPQqOVL053IvrJ/A1AKrd61oofYh+ti5wv+0e1nxwTXQsKngqbTfHKnpaFsK9YQnJDZONrTTiVknqbTUSKwQwHUSDLGVkta2NntdmzS5WSE8Y8sfWqHWFRo6BilsZk3VFBVnwS2BI7eFVi3+RKMqViBIQGjTAhATQErayFkXj3jPIYWPMbMFU3Dz+FdB0tsMIZoieP6PsBNJ/AnppaW0xFNX4f6QE9yAK5g97PvG/yQu8qGPULM2cZMu16Ga2+vDaPRkvizTfsyKfFmo+seDD9w9FrltM7U0i5OTNVZRhtfHTDGA+iIHODwoykbCWzI9uvprG9b9nx6Rj1VnTb5gVX6XQJr27ivhaYyWM0HRaRHTpWjNx+S/VixZc5Dx7TTgIRt0qXY/nxoV/E4g6GxjOwCa4o8bVBM7irNnPTC1NHyjT1/jM8boo6i9tOYV2LuLo6LO42m/5aSyVbgoWXgupoAcUFvCuJZlxOUZBu0PotrhfawaC047CzLTObpezuIbfxMTwbQhcSd+LilIu6vtxrMgmR3hWL3X9hG6Nel2XBcEUM5lMRMDwxPgKRsqLGmhV9AKjoJ9cjhzvtGOmJ3ZugUEANXyOkArIytBUzVU54Wo6tyLUQ9mIdXzmPByyFFPgim75aoIoTYqCdmJ917zRYmU5fK9CnUkTO7S16IWmzMBCrCXHgycmDJGqpQGF86CMrdLEq3LRjnVKmpTpGYmt2NV8bWULQOBpwNA2NCnCDFObALL75cyjRjWIsWnhhRab+5/wy4Q+ckOK+tCZ8oPSNi3AtPNUAFMzzeDuor1yD9UIb43vCmVZoOaSJkvA8uNr1tj4SPUJQFo8XfsaBCZXm4HEvCncLyZJyD431uh5UZkVMJHq6+jkeBGUsmrkaUrmalvTaYSTy4AqHxjqsYY+BMaAWmRpdCk/gOjMjDCL2m8RXpSqGZyEyeVDGjPmVTDGb6sH8GSABNx2bysT+Bgl/zIF5cfGetZolPkpa9M9zU37CCMzzAq4r3zENYc/BfCRNYJcC4bZayAsCS+FMynNOdxO7Lukfc003Auhmw7z9HOY1QpJJMVlFUA9ro3Gljdk1lrJVmkOfizahKemM+5dW1oR7OTMOZ/IGYzUpibTnysr4j9MVFVWsgk0g+AMIOu6PPI54X1lOebW7Fu1xltVerNw5jKVbWva03+YS5Es1yJoKbKnsZGR8h64yr3xT6O2T203q9X2xdZb1OywG5rDypTOajLCudJytAL0XhRDy01g8Fz7wM7VTJhMLCGTggOoCm7U4DqQD/hhWvGLukS2eH4JWNF5JsU9+hzbljBnWrtHvs9XfuVX7ivqCzxmjtf4mBgm2AKgPQiXaFj+mtCLql2jDAh/kzACaic8kp98rCx0a7v2q+7J1vwBgOF2VYyl/T0PKvOe4MzC2WotO+tY7mgrMU2sL/BZrHBmIce6mgfP676EK4ecaQWvDvC93h5g7pMAJjFIrhnVW+Zkbgzn2kEVnGO4mAkmTFpYiMzzvTKp9fngt4GAZsQ4oQsgOFxNRyqRXQGFifFa5MuHBINwummONEagq4nz3Tajq2tmu+HM4qGtzNGq5S676A8B9AHw4JNMa5mT8sTdJ0p9hdlrAmDCZ7dRl1KBTkq1Mic0RYBmienwrQBD6Z9JBZpwyL0WugTA5IgIaTKTahJpmad92qe91WGgtE6rk59GQxNUA6aWwv1Wo8CfYYJF70WVszVqAt8WUgIEzN60q/oM/jDCqUWpC6aAZLonVcpFaYoAgGFMQCteypzPOVo7Ftxth4LcqunX0bCsgmif8nHtAeAEMH+VfNDUtPRcDAV2d0Svs5a156IrCWxRq3RQUVhYU/lN6RCDMx3ec+wvNQe6egnCz3E3iciZj3rUo25jceS3+RzEA2eyQjnBfCmDzEXwXwIoGQCY1VypLazcj9k2i/llbpltg8939BmBJHDOL+1F0Mp81Mg7DiAt4tpMLEaJnswW9OwVMtku19EpczWtE/bwmpa3mKXkjOfccHnWMrMK3JUZSMZSvoPEuQKzRWbSMExRHc9DpOtpS/CYAqt49nU7x47K8zwmhZ/G94w2VPNn2rgJnc5+ILBFBGeTzmn/WPc+Ow0c21NiruT8KlZCViQWBk0XsL5uklfOtYlsszufG3fXJhVG+GcbhybzusZ5a7+2qsiMiVZiAG1RegznUnk1XOTbw2lnQBK1fQr4ZpRooEQiNIfVFt07DRc7w0BJ+gJcJ650HR0vT22rRdswjzDCmjpHmpxBwdylehI5IwjQKJUlrpVpW82rZ5eDmQ0p1RToy8fh0+WIxwZ2zgR/psxcN1/SPXANCCFzLRIvE5LGvZctamcU614EZ+SBpqsdxcwpuxd5ZDBUNLDmZ2UJPbKV+K3dPr+ilqFzQ97Qd+g6P4aDPKOeey1ws6uRYIeja3G4rrTJ7FCUDzq7ts+9uJhigYfUT4M04ZgJQWzVA7QPwyRGGnTm1jiiwXNRSovV2DuzWpanWoiutXEWGdr0rkBtdqu6l0IXimEM3As3alLIpqZrIfOHLZDyuFtdtW6LXEPGqdN4c0lzAKGJjCWMZaAyKSjhHL7c2peEaeUGzD20Sq63v1ZMiUljShsaOL4fnFEetRK7mVrbqgFYt7OsdVYBRpw/phVcQkOU/Zi7G7aRcIU4WZJMv/uwoPI787XWvjLX7SvPRVfLiBnFTusxd+UWcLA8ArtpCSah5JF1AwsfBAFU9zg3xHBCvobPsGQ1v+l3KxPkXgnhFDoTKwJNO8Rcju6d0MXkzRyYUObAa1qINuEXZhrWtNAhYHr6P2szGwAw6IPFMCnlL+dGw5EN6tuXBvReQsfayPYITNYOVtet6dZUaFrc/YjkYZZlbuZ+u1WPQQ5YP0HYViPKWz7dfNNrIbJwP5pPbNsGSwRG4oGbTOtEm8/VCr+JJXSuI4d81rqGg0VEnLsFxnqueAanDcWoaHWLIXPRIpgOufFQG8Kxhr1NtnANqOMgVgPBvFYfkRlOK4t+KYO1Su9ej/WkPMENAcXkohrZuRV95M6ZKNja9O+RtTeaE4nk+DhlH2bS2nMhPbwJEk+iU/mHOm7fS8iEyWFeo6OXNclfm3UQhfb5prFLaBvRpRVaCmelyZ+arus3TCzfRuWWBUqg2i/DZFUI1KJ2nVXXdb2ZMDAQIBscMzG660g1niJ0BS3uB+4YtSkXJvNKkwPfZVnARoc6NWxGK/w5Pk7+T2Y1dUqrULMYs7El1k5I19HR8hRHF7zB12CKSkNFtY4Fk2swC2RildTnRIQokJgdoS6jdVdBNVFIpCjmTA7NIPAqep7bT839z9rlceaD+c5tmT6F7hwbqkwBJ/QWJm02kYAWErkwD2A0OOXafq05e2QCgUm1SZTEnTuuzDYNpBziTt22kdlFHP17tSdDVVhSUCatGoXSdVWEtWCayMDZFlTNGS/TOOdQ5drcZJgmllstEOtaZmuJzKwFwHWJyewz2tECrx3rrM84h6abFpCCkdPm/2b6ZyFUmzqTHbW/a9/oO6LXMCbYEqeVSShkn1XySbVKeP5cTNf7JXSe83XURgAnrbb2uC+nmVabfUPq8u410BOSXn+Qq/Ye3tq9m6AYTxFsBcv1CCH0pZLy9/JD85EEIYKR6iMms/hcu5LnNrkXC1PDJNdtnJOHhNDYKshmLVmhLSLuIyuaToXLH0bnnlSdViabDkwNm9pKQJ8DqwsHcs00geCHT0FbmFyTJ0JNS5edyP8zsUwFZx/0slLqr7qPxOpAS6tZFK6t/btMGqHL55ybyHV90k7ymVJy4WVXZZFch9DlQ6NycRX49m39XsQdisAHzd9fF8ltyf42HFGAs4XDtIUjxxa8sAX+nVvootJ4lKrR9y0mhOuNBVyU1ebEXqMjyajIjbZnxd1q6JW52zYHqrlUphm7tjlwHeWASy+Cb6SaCB+WMddh4nJbpMhzBW0eLXDECAvCdUfnnzXPNLqAo4W8FmM9svaeMwHSNrPQpBWY0IlcSXK+4JZ5PZfQASHjb6E2IURih2Dzth/qLL5O2LgHnGIOb03+6nJ5HeyXWXLXpiLcALQr+VTAe6aVGeWAc2n4oyJp2hd0BXhPcCMYXBcz+7K+qkdZERiuepl2Fp/M4gIhMBaccvIP7+ja5CYMPCYsx7eqryl0IeocW+j9FLpjO9bcS6Erg5CvY5LkgvlBIlIBBp8N5w9jBqANj4Oay7Xmx9VLd1Kt74YitG4wUiTn2gRqNKxcJv8IUcEjqEFAw79s6/OKa7q/Sao455agnc94qWITkRO6uRlKRBAywlpKAW6a1+no+UNtC/DMrL6ghkL7eFQoLL63dgQ65zET7vXynRMyW2EBKgG1fCPBD8HMLG8N7HVR66uqryRy7irkurgyEACcOQ46c+Q9DnjU+/qNrJVt9zrtuOaXZ8EOC2Ehcw1mK7N6AhI+JQ4IsqtWvhW9dhNuFotWxFSLq9lFKCBTUhdulOo8p1O71eCngvDZ2zctU1dx97buPtPnk9N/mV1vLtoBZ2p8520X7jS0167JguEr0bQTFqkwZ/bHm5jovWJmb91P4+UasaDhuPzjGQAVJBE6iikZWVvP3eaQwmFw9/lDValPClCovuhFon+r6c5Wu7FzmYDays5m3BcRHKf/daiW9G6ZzWul/dxG6hBPb227Mb9/rvGd52sBWsBysNwBiinIJLyO4HHNtBPLBVthtNtQdDQhhEE+Rv3bkuQYGv5Y/g16v9XUcKtt6zmPqxQGXSVqPWWvsbWl7oQ8ZjR6ig98yu6I17mAQyaKwLNoFrS55/fX+T2hqyyR7PCf1QnPObnFMplN8+AqilBEp1Tn3KR2ItDKzQQchzpp3k+hO6dpP/X+ZkS77lV2jqDrqoSKugMUCPWeqjYZKT5dpjVrSGa8z/xy1dbOC7d8ujQDoRP1ETrSGtmxCCWmhoYxIpNVq5yrPuI66mbPeQ1rlmIK3k1dmLNPTL34iqRhjlAAwrV2f68OBMIxNd1UULdRZBK6aV6z1UWvHuFgTpyzez+i1wfl2NqB8TKEiPsllNOkzn3UBESwTVgukHv2dy67AjQGVSV0q7txWy8x4GpC1x92FL2uQrfVoOX/92NtELTut3CTrMGpm+vFABZdM68wxiC0qekI3xS6ra5gtwkdTSeQAPwldPH3Zyt8aZCAv2Ndgf5/MaGHdvc5dDyIC7Sgh6bTpoOmm43F8+nqLgrrBa1sycZtPh3AEtocZDK7FtW6lNCpgZSimVjSuTMS5xDIy0bAa+HzOZnU5xC6lAwwG/hbv+Y0XaUColrRq1z4JPfeUYJogAidSvfa9Sd01Re034Gu6XhVs73CRa35H1QzeZl7mqWIp5rRB2Wc8kUJXczyaoizhu1UJMCA41UPvcJot/0xcFjVkRSHQKKWAQldbFeRi8T6xGAeRqG7bJ51BgwPit92WaaJTAphIlQ1B4qfWFaC7GD7IHLOrqu3cq/zDekYFHROYEW15dNqTU/oAIOzV9tW+P+gCd2hzMVFmNwUuIiwM0p9GLTcFDypO2WVfLb4dBFDIsaSHeQFIPLWArwtaUzocPoBe6R17S0c6qy20Ym39jh9WLXZKVmQGZ2emlK76YK3puPkXiX8sXaiNq1CJ7EgayWBsOVm3HbTkuKkk+qUP8sxrFA5ocORnxjMRJwfNIE5NdF9aLuBuWv1uk3nyiK+aFfCm4ozzjYb7fFLBmi6MlbTvHpf1gqet9W67LYTkGK0b5FJfPdZEZ/QIUEqP1wj1vsRtR7bp+LUHWVWE7mltY/BIWvL1a3jovFZ27vepACiYnpjIz+Peq/4hkabxdaxn72PxKkMcYvUe9vE1QSalE4Jnn1AnEThBTry7Ax5t+2qrivCnNH0OpGrgGxtbjybC65d3OfW4e1ZX3fJLSGbTXhWIZ2EzLVVxaGewvcjQIu5E0CsbRiCZo2VJk5X4p+JlcOPrn5HYc7k09V9U2FOPLoapcz9UVGrNVNBc1n9l/tpLkpMV1OwNaGZw6LMKTT1IcGkoPXdXxuhGGyDiG2sq4ADKRRB1Ge1BmN+/C5G85r2WvuDHNo1e90O/X4J3WzE7ZqMAfRCYU4lnnNn7mRGr+IKc9brvo0t24Cjc+PqVw3fNpEdBFKNQR0q187g5xyYufHJ1CyzWmzdW3Z2sayTJkYx9i6eoKp8i0rmRRTG3YBL4Yjxd+eBrAge0KoMPR7dXH0DNB6s5D9VUBmntcVCgUf1xpN/NwumJr/t3LWuq/BZZCC1yTpKKSWAZEdAKtI92l19TqCim/YAa5O2ysvC6gwyR7HeH+suh+fWbmtF/roj9mzSR5trRiOVB3Nyv4TsMY95zF64DKr8M7/FALZBXCWD81Bc4zMrX2GN2lsZHZCCSneMHG0vrHznck7aop2h5z64c+GsoOq6b+s5ha7nFqe8K59+Nv2pfVgoh0aakgeTDDJ5m7cJXTelULbtF/1Rmq5aUSczqApIahN2roYuW/5cGmvVBPkjzJhHZo9JpIFoc1rMAPFRIzRUrN2esW1WN3cvbDHOPTUal/X7xtB/E0jCTLAJIMIEs9zmdjnqcy/WNYV0rqh3JaD23PXS4BZhm5nUKau2EhYiSM39Te02aXC3Ierl1xRUMBu1PoiykpYzwEgBal/5O2sj43PiR2unxxoGzmtRWQUKUmmvvkO4rwSwDUvqAOB+20G6IwFLsNbuk3P79i2hmxbC9xWqE3S5SURIUR76t46dCVlz0YLZMqnnKMpZFYkSSlq7bagm17J2tTQ/MoBS1nXnnJTaHQ10PDKbIthwuoKIOlwacGaEz8OvS1jXvm3nMgHTQc9PaoMQPpqB4g4ANGmc4B+rtR0Ku7eKstcuT1ObpeFagLMLwmxV1mT0P3VIqHceAbR4TRJKmZwm3zLhS+PNqPicbJlZoORgWtsLdm7UUn9nY8lqaBVGLmZf6NkW+LaV0w0q16MV+DMzgJhhMR+G/+NCapRyvxq7ZDoFQbFb4Y2KjLgJNXec20d2HzXDtkLbiXpuujd3v1k3rZsrve5Qszqq80wh7pi1Ba6Pn0TzQftNWGZ3+q6zk/u9hknW81AsggMa2oKZrkV0dWOsz5/EAVM88c5JCr0tRK/QmKqXg0VbT9vNHnVpBZ+rf2Vi1+zEuZLss7Wo0kPFzITNBJrINk9buze5p8xnAzgFoo3ppnbrWLXeNLlT4GoxO9uspfXmHqp97jfaNYiGsX1oaqWJFtHW5sH3Wuimz2xR41rq/dLCnDtFdi82dBYs8fXXarI7NF3mtcyECniJ/xpdp0ar+HFoCCPyq+vi/RI6AwI/w2pg8vVz062pOszZdWoKydqAsJYI+XYrMzZhrB64NhUVGs8AY55jtufYEroWRT1O2lgFQ9s9Gd8UwrkaTiZ00ZnAPsa2e22RzUDKdaO9cRHmlu8TTdgL3VbJIJ9CpyFOd5HKbDtf10UDpnuTFbkWnlxF8E7NTZYPLCICfwhq9ACxSHABpWLWfVwTmuAOgsNU1AbWwInA/L6tM8MlDShQPGiE7+I5v6wGMm0ozKF2+I86X81K+KkJ+53/8H+uh2/k+mlpGCE0geCtTQavozPBRRhodCadCOwipMFPrV9nAFWPZIFReeiJO97Rc3irJRRplWNjoghdJykllllCc2Jiq7CfHT3vZv+CuU/9GplWqSRY0NXICmTqTdyk17cbTe+1t1WNa+q90Wc0N3yOieAw0zSgFeaauQMXgImckwaCu+EfgkB8R2pQjxKIPU2lJx1Baq/XFu/s01sDHY8WeKa/a3MP/geOWAXe3P/1UCHQ7IBwlU4FE9Gg5Vg0FV4tSNdpUbhu9+UQFBmLre4Dm93V1wCAybLCnKiTZBZMWvszEEqDXSuHqzRGXL+XcJXlaJAnT42jStj5P0DcGM7tLT8DhbXncKWUViYfyqT6H73g+C24guj4ghEaBuTSTjrtRuiw0AQv/Bff0ZPX1p4iZgKKFAEcFnCBSQRmCXwmv8U7tzzKHFeB5wDWuz6CZ7GVaWlxFh3OLTt777L46Zw//yOwsQhdQxF/m9BNoWMZReBb7UbuELpJyekLbDKnXDhfvURqtA6S1KyJA69kx9e9pa4idHMB1Ain//ZaRsGKEpmmRSqZnI0G86mKIH3nqZ7qqXZP/dRPvR8waS1mmeYCGhOsdVvwi2pT0wblfOciaTEbGwuEAIJtjFk+XBu7OQKnM8m0pKMF7juUAFyv4G36enOX767pqsSJrI3FJZVHc7eN+hrZu1bXqA2aRTe77W+aV2+0WcdEj51UFPvYxz52P5HTnwtmKPozECTcCpy5tqvsgriW78lZtreDQeS/ETgpplqlJnQEzGvazGqcYK/PtNbXaFB+tG03wUOEOIFJi60g8xY3bov+tLJNakFmLFF9nJOgM8HSZe0q2djWHb4xb5fE8D0TT+soetHhySJJo1mcc/umU329FSKZTBumlcVrZ/O5r1kYrutlMfQusRjSuIcoYbe0WqyLKfV+yJeBvVQrkeObaWDjrUZSzuTNFXeViqqt167D4DJfertJtNNUpWLWKGpGmTnsTIMUFI1DqxE05nKSAybrZIt6tBU9bpmR+Z0VW6v5tVQcLBRJgIviHghYmi/WdsFJAYhHgsep509icnQNMVsObRh8ypinJRNYOCxL1s7mExSfvrJOX75b+m7ufngHyyRw9VDDPZRjvXzbpbkTJu0NiJOCWQjH3Pr7bsP8hJe24MTLXxJ0VOlqOAwIp9YglDcN9af5AJo0G2Hje7rGJqi9vKZpPNTy69R6iS3/KDpT58gE8RlpCAFZO+SEIRYYtbeZOfAeZm6mti2R1vNNM7ul8Q7dy8r3Y1X4o0FOLeqEjkyI5rW2pRSqjZ310HcIXY37ZmedLthBe9EutBkzVuQ120MV8qMx+/66jdBlhS76d9fENDEnHPI2zojNnOC7hjSEz2kDPh9tIso0uZmfBmX6QCtFPf/jsi0g1v85xNpoUl0Tl0HwwVrYvK5Jncn0Kq/cY0GGhYa0wLWxKCdQHqR0ChN5K31pjPi4gpe590Vd65t30A48V+DEesyuo6tZvU3o1pZWkwjJT+NImsAgk3Ct9nQvIqTyObl3m51I+3huFYsk/XfdyRO4BqKKtfwg10S74bVZBKHjCXSabTaIObTL4qla7aJgYxbtpIniL3rNbzXOcE/BhnuoIU1ZofypNCINKCLG5OWbEpTOGXXqMh1Np8sAvbAQ+MDGvC3UtzrUazHh/G3nNKPfsikH615LhU1KttfgACaWtqufSaZsZin4JnCtmaS+StHM3O8ds4G2cu62jAoSScN5jwagDUwWCERESou0A7XnHQnbVbcgX6OxY8U35bRjI0dxn/BS0XklfjSzyHpmSQK6A7Uzu4RBQPK4xz3u1i6JW77ksbqMCbh3Tzh/8M82scmfC1B3bc7PtKKm1695bVN7dOvN6URWD1DS2R/qNWYFtqGJY8IUpXkg6ATFIB8yL8dC9fWCIeEA1/CgTHqRVJkEgyLC0vICgZCGTlvW4jWzOuk2xxpUH+OyHSq02brX7uWQ3zgbWnsUHEiu0yC0e+5Ebo3F3gYo5iEMr5qEma05tRn3ZF07v4CLdXP+ylA7f7sgGnsoQr2Ft4ruJzjdOe8gcRYJNQhpPeE+Z9EJi7LaXihT57lVR/L5UGmrLed6qy503djN4DGtzlsWJBOfb1Gy3LX4Ht7c2k1ybjswA4OtDdNWyOOyPullevSl0SvxmxsH86dEuFrtSrnNxS6QiudoLiThLTZjPvHRU2lmU0Cd25iDldruavazmQud9WHZSoNu7dC4tSnzI6uf0ckzCzncddWmbtvmkm8RXmNQIikiSXJuaburFi/nT/FzONj+t34ZTGmgr0hOZRI4BFt1+jWzimvt77sC0cfM41W6bm5FwIfgi/y78pz5m8acXwVWCf0vvdemLHKhgg/mVcA1U5CnLIAJLDdegjYogXPRqrPopjSoa3Be0bOCpDUYm2b1DqGbg7oOyro9en3J8uHin5UGKbhwYTa4AFFs5QRPKfDtgq14pgaT2cCXDHc4F5OqSAi0I2AogzHrD2bQcIo5vO6ilmMmu7TV3H8rOKf7F5xJMTF17QkbrmfyRbDckImNHVosa1et/DDj47lIGi7HN27PskD28tWeG3ffkyJba1Euanp+KdDWShIaS67nV4XfZOJcJIce4wOwnDO/xQdbmz1vmTO/R1vyXyCTNpgz2JLzfBnagA9Xq3yR19zNcILV56J8X2bPrbngt8iTAjltPAgek0fLGQcEAQIH55tZlWPdBOb2APma7VXhPPLoNFhkg3aTjPSR/wxX5MpYFJcd00sNjoujvVC/YUTVERTGF116ZO9pRX7Gult0Aub/0kpBNavz67sGxHlpPDs8Y1yAFuCHEuAc3wbaf9B4s0Js9StvWsPGNeorFZfW8lx6iSmz+NCHjAGKu/fcfz5w2zltBRGTAl++vXGzUAUEzGqQTHOZSc+HZ3GkRymDNPJloLFLDZyLlDpi8+vsVBuxHM5ZxALJhpW5uBzcaTpbZdPEzBYPc29TwmngqX9FH5xXgkigZ01Bm4LMZPdNa8C9JQjrxilTOwf2wiwtYuwXB5TAe5PutQXJzLFvHrMilRpYvIIRwlWQNsmtbZBM48kbM/lBapfFYi+9cq0iEw/GaPvvnPows7ICzADMDFXIakz7zKh2CzWfm3WssMZWIDA1Z9DI1Bw3vV/eliZeg5vghxkYTQHq+Wot5u46My/b3r40HMFlVqtnnUX2wSShFSJplC1g8LE0210L3dQUOZwkHY6T2q3i2wVGganuU9gvmp0O67Edai5qMLi2Wp3leg9it/dDPfG2NOLsm7Juabm+XqlPczHGpGE9uC3yuMEiZUCi5ZvPRz3qUftHvENWpiKoq9RtXHqA2sRN1CJCFcVUxJLQFdW2cyLVDN3mqFpZmdT+a2unnYuyBAlcjIZU/WUYFjdR6NZ7X7VcmoXwEKK5C+WhSHUSMksxtt2octMCtDIewTG1iOO/g6b4e3zK9jjLrbnsGF95A13Co45CUEHlWiWREuPbtdOOzIVIE5bEv0vjpe6PrZitTksrE2KL2h7O+CB2u5yL5VgAdFFPwC3yQYQHixThErhbirFUW3UkZZyq31DPGuh/N/v6XioK6wYjVJYe00ZAFFs70FDrHFLajvABjaVXRJezE9Bl1fRc+Yf6z23tEfag9EI+pXtn2u7UPiSTie13fGw5bS5Sc0XIAn8JHyxUIqACIXUhadfOfRZNN1mldfGxWgCXsz9ZmE5ZhBgSNKOa2giUh+hF6+YfE1yddOzghotufgv8flB23JkpuWPEyy3wPVikeWNdCBw2MCw1Hy7WSkFhnD4CSDApC7ndyT286pheehDW9k+F21gRUmQu2o4pM4otV1dXH85o7N3JbZuDOmlRWx3My6kmdKf2Bb5p0MkxYuikHU0GyGrWZvuJQ/T5UpnG/AlPeMIe9ghrnW0xZn2w1+ZUTtvv8gWn33mWQGLdsKyOAPwDjIM03Jo+4SPEu6MVccBgTd2AG4qPleldtVeO8AwYLjKZV6Uv3c/o9RjCf1GQtbVT9+TLiVQVWwkcYn/zxaEQ3ss9Mn9eo7QhAHCJ1s2Nr2o57mpD38xsZXh8BH5b3Z4yqdFyqnrynlSLulp4T2V9ObgTg1rbEpxqTm9CB8u73U5g67Mt2tRaVDPZKh3ShCwSIZJRaGvVLJJ5iZyblqNEmGFabmrS6R+eRehWv2uCkaJZ6RGarEKZ9hOjyh1u2CGHCDgWEeHWE7yiTY+YCytGd1NN5HVGrVv3dki7bRUEBUXNrI85Uk6qv4s5iBQqSIgdFFSSIMqvCxKVT063ZjX7Zxe62Xogfw/uwweoZE0ej5ARRI9UdikzCWv8uza4K1kfhXurZcI5W2bdjy06TzFZTXjuzRpklDZrIYs6AfRYvqEJs9NUPVSySqyVHDf3x3+kXHJ7ZrvfeyJ0x9R9K212NAej0HhuEs+NRoPjeewm4//Htyeg0mroSXUp2lrJM4otEntYtoM6Vei20mGzzURjxlWhpSTxsVMs+JhA1ZHUVQpdqvoHSsJcyDqYy7TZFhX9ngndsT0XkvyezxSNEBv5EKhYx8vYrhoqEsgYx7QgcgBWimS+m13bVMSKmBp27e7+sJjXi2hJlRTMgube77VCbP4YVKEumcY+aCTmSP4304qBzASHx81c90pKuJvdLq/s8M593WdaJsGABcnPipRounw7K6k8rcEI36tKXKspERZMaBY9r8l/zytmeVh2XDwU8Kzd2AuoqqmY9HuBmBSlLgJaQRC2+I5R0WL+zr7Jj370o/dzBU4RdEzXaZ53C5a5Z0K3SvbUPn0WraYVKJmMfIjwl08Xxb3ikpLKBsFnNCAcTyMb1B0gcn1MtmjfD/tui2uaMOEyJizCxDK5JlwUdDICR7O1q009X6qkm43LmVpkUBV0/Oncm2m2J/lzjvs913RbVJZW2zR7Jd+DPSSJ0c3rYl70FGhMAAkcGKUi43oai7qmGa9CreT3MabKg7ht+erjzc4Lk740fbkcfUxe6arG2FjW+rbAIYikeoc6BcgSxUGc5NcV91sX/D3n083QeWI1K7MjzK2bAImgVOtBQvD4D7XMov3ah6GGg5lgAQbkvD68fLiJys9WWDPxv1Z5PWj7xq6LZS3jm1CSsVYfoQJPWssYJnCluEpHRswsVVlPFMJapLv2CT5GRpit3O55RmKd2Mn1mtsgtQLyM+A+TC3/oaouZpVJ5c8RNkIHSqlBj/dsBYqaDRkHVBK+uRoPXeODoOkOAcJbJIgZTBlTee8nPelJe+q+XjLGdBIuopfXeiMB9NpCF+jxuwvIJslzpVZN9GDN7Z5F6FasrOg1VTsZr7M+wkGN03hRZmg+QpimK5oliD6HIT3N0zzNfgCF/moCwo4KJOa+C53/QQOQDwVEq+tSAMHfZQFgahZv7WYJm0VrsRqzp3iKp7jVdLHGkT7jwynZJDTxEbfayW51MTiWEbknPt3cqyHNtqVVZgt6F8pBJSSInARH+RqOXUGElUfY5kqtuXZV/bA+Taw1F0SBR5uvieFW85oHMciYvtx0YdynQAGkpCJPOguwnkarqc7cTCW/uTYQOl2BRWw4SOBmY8XONUHgQxpsullXSTFeSeimdjlEqenCQs3LWHgOg3viE5+4L5Bu55pyflZppYyRQGMl14Sa8Ilw5Xr5I4TPf64h/lX3oF2r/a9LgLdyqOvEzj6BCQFhc4+AXpGpoIwb0pjMNmLrbj11fqLdMEbku2WNGifjNvfGnfUXp0TUVxmHu95VZXZUP9TguuzBNLUEhAOMi6dHigF6yqd8ylskgfCjfL8Kf+p5W99bVWlK8mjPdZ+yVvBlhGYC3+WVTzUhxyhKaxHSek2zBnXSz2Fm/Db3KB9al9HGJwRgprYIWLicDgDGDoRSk51A5HhxpxRKX6fVuLKzO1Ngh6q6Zqqsm2MmApU5sHyT2qGWr50dHmsI2HttRtJ7BlinUJrPxPAZ9V0xWWvh8ZYGuy5Nd4gJsu55MRfpSsUvMrV3LEETeHFDMLP5vdGRGqMIl6UTHZWF1mCHn8wUQw+MdfUN03LN/O05GDlXogFNoHhtk7UeK/dtLaEjgOompM3k/JgAghSIWZqGoBnENg2pteuk5zDVikz0PjHIOH4yG3VwamVPP/RY182E4pQuU4doSGsp4SporsniE5XrpSfJrq6YsGHstg9Xu0jncqThanXLGtQqFiAMilJIg8XThneNe9ezVWl3juPKZnWrG88hx/jQxE6tSQNykm0ep6Eh367m1dHg+S/qMPJjTEZdBbw2MXw+jwad6UW1grQb9EM9N2aGpQr5quynv7p2lpwg9YSMZoC1JvGDQ2rFRqshSNDQNDWtJqLvfiNaJmAWYxqPVjNGvitYqDjKa36f6FawMLe971qv6u+eRehWVsllW6JehEXVqDAqDodZ6gyzWIaiqvL2fih9Uwqt9qixXWcHcKZYtAZxBxHQgHatJoScaefC2ysCnkHINIOHtNtKr19bNkyGrYmX0pOIR+MiZHws18S1oJXad6vKrO6pRdcetPWIC+z1XqWeFqxgwT3S8jO4qgJva0PmcxJdLx3JrXvSX7XCKUC5LpnTjAkINDY0Ie1iWE1tpY2e1+ClwpJoO/VRa9ulWMw0BJhBcZAUG84YcoEgREsymRN0IFqxzUocddAMz4rhHP9PBNh3Xbvf+g/m0n/SZO7HYgJy6/1mVx4YG5iolly0lMe0d26D667aPq1edN82BiJ62QWLymJyLS3q2dh7ZV2vXUXPInSnFLRsaYC7WRnrb2fT55nYN3Byr4SDsMTnb1Imn38yJhJORwFJWqHfxGYGQqNVyXqYNBpWEbmu4rSR9miugeAIUPDMOOQeveYS+Mx3ZEx0kNJqvy2bBDgiR1p77pgT3LFuWNwOOmUTptZzP7XWZ1ZrZuMctolyHTT3mrKa3bG2tPS5Te2lhe6yxRiHOpdvJeon7hd0wecBZCIN0BAmUMosjliYVBohzlhOdeBonTxpEr+r3C4fiQ9JKPy3YIYWAuXIZ+KkSd+ZXFkRnDOH5wTVZzSX78m2MOciaoFNQVHU/XWX7CLNyf6oY0Kb2AX0zj13/bfz8VkFCtKMAqZ4cFOYtoqy7ydwfrJpvWrfivU3a/S2dqPc2j7cSrWCRXbMB7KnSZ39eNspeu1EXsHJ3DKyarX8xXwimscR7yyTly9VJJ3vmIZt58N2X2wXxIqVY9XMbaPqbLnuojg7XZaVmfvIEmIBkqhUlMt8M/EXBW+H5vWq7c2uXejWzpGX4e9fRhjr5D7b58+exwljAs+Pspo5yDqQi/YkummqKSBFc445yUEL3i8AmWZtRsP5S/N5/mKOfIHM3NN1mvBer/83NyhO2OeWR23XVMdRv4HT0br8XJw5FqDOoxMznd09JwZ3LGW5BfbfS+HbpERPU3rdF3GoH8e6Mme72HkdBo5jLIerfBElW2oIj4zfx0wWWMTVKwJcBaUk+NYW6X1/CucUvPXo87mn62yjNjc0nuBujboz/W1TYGEQNIEUzY66ZKHxIWn9gO8teGYFtY+hDse2IziL0G35b/e6UPlYPcBMB80t39fKflgUmjW2MWikVvT5TfVEnrtz1+wvASmFVMCRE18UOY+5D9khoZz44roZ79yuvVauk2DJr6TV5KZlJUTXIuHZxHumF+d4bC3gy9TVnlXo1g6Y1xGl3q0wbvkd6y48szIKtAHyEHHaC0w/YsFAAkjwAlTrozt3GKz2c2q4jiLgIJppUldhzHR6XkCwtet1IDe/TvBC0HTDfPzjH7/PplhM3AluRUHWbC+xsn7Wvi83lWVz1LTeVE7avNbZPrZOnBzrQFib2GGjwOWYKUJoguV5CWP+XREi7VbQ4JiR5hSoyeZYA4t2mCla7TsEk1YTefJFRbqB1rpbMp+CJcJmAc1MwiQEHKIcbYH4N1Lo1ozDTe39sbV6V0qOjMYs1O5+CGH9VmBoUm3gF3CHTACcTuoJblfriwKR6Y9NoZvCl9AFZ9Bu/ot/6REUo7WqczmnbdpF4YBpoDQhqyBmrZqfbOx11+pTC7NvnNBtJaTv94We4oOs5rYUVGWQpdlmQVFESIfoD90bvQqgK08pIAHoYmXA4eQvYW4gCpoJdidYsVd9h/cJk+8wjwgHaODMpOiamQcyy0gQengaepHIsx4uM/976n1fxme7cUJ3jhD5bgTvIlOyfjcTlHZY28JO37VcpDSWaBjmRfPILCCH2iaJeRYhS2FhrtCU8+B/eYSZ+R6gVlAjt8tUJmSzrmPV3nMDvot2nb6oY/yxAp8bI3RbEc+DVqS8FgnV2p4wOdpXIe1X7nQGTdc1QWuT7rWB45qhmQXlc4ush7FJ0KZ5fVCLkVc8ass33dKMa/C0FUAdY9AeAtBn+mmLxXFZwPZh6WLw0AjdKRFc2qZjblO0MmhWwTnWaHols24J3doWY37/WKXV/cDPziZ0D9sqOtSVYG40XLvZdWfEGZTMPSwu6qK0JXRpssignfPQpnhbHeQfVhP7/wDFTB7qS2YsmQAAAABJRU5ErkJggg==', }; option = { toolbox: { show: true, feature: { dataView: {show:true}, saveAsImage: { //excludeComponents :['toolbox'], pixelRatio: 20 } } }, backgroundColor:'' ,//设置无背景色 tooltip: { trigger: 'axis', axisPointer: { type: 'none' }, formatter: function (params) { return params[0].name + ': ' + params[0].value; } }, xAxis: { data: ['很满意', '满意', '一般', '不满意', '很不满意'], axisTick: {show: false}, axisLine: {show: false}, axisLabel: { color: '#e5435', textStyle: { fontSize : 16 //更改坐标轴文字大小 } } }, yAxis: { splitLine: {show: false}, axisTick: {show: false}, axisLine: {show: true}, offset: 40, axisLabel: {show: true, textStyle: { fontSize: '13',//字体大小 }, } }, color: ['#242424'], series: [{ name: 'hill', type: 'pictorialBar', barCategoryGap: '-80%', // symbol: 'path://M0,10 L10,10 L5,0 L0,10 z', symbol: 'path://M0,10 L10,10 C5.5,10 5.5,5 5,0 C4.5,5 4.5,10 0,10 z', itemStyle: { opacity: 0.5 }, emphasis: { itemStyle: { opacity: 1 } }, data: [0.339, 0.441, 0.195, 0.02, 0.005], z: 10 }, { name: 'glyph', type: 'pictorialBar', barGap: '-100%', symbolPosition: 'end', symbolSize: 50, symbolOffset: [0, '-120%'], data: [{ value: 0.339, symbol: pathSymbols.reindeer, symbolSize: [60, 55] }, { value: 0.441, symbol: pathSymbols.rocket, symbolSize: [60, 55] }, { value: 0.195, symbol: pathSymbols.plane, symbolSize: [60, 55] }, { value: 0.02, symbol: pathSymbols.train, symbolSize: [60, 55] }, { value: 0.005, symbol: pathSymbols.ship, symbolSize: [60, 55] }] }] };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
离散分布水平条形图
Discrete distribution as horizontal bar chart
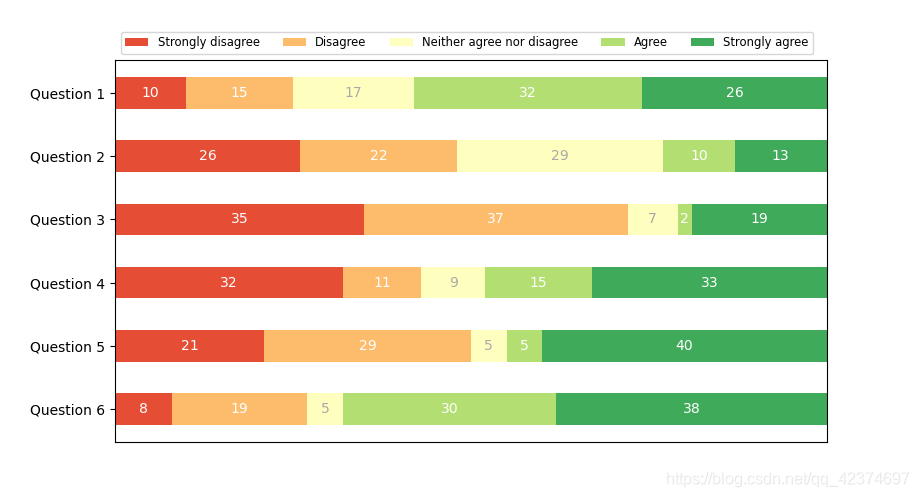
import numpy as np import matplotlib.pyplot as plt category_names = ['Strongly disagree', 'Disagree', 'Neither agree nor disagree', 'Agree', 'Strongly agree'] results = { 'Question 1': [10, 15, 17, 32, 26], 'Question 2': [26, 22, 29, 10, 13], 'Question 3': [35, 37, 7, 2, 19], 'Question 4': [32, 11, 9, 15, 33], 'Question 5': [21, 29, 5, 5, 40], 'Question 6': [8, 19, 5, 30, 38] } def survey(results, category_names): """ Parameters ---------- results : dict A mapping from question labels to a list of answers per category. It is assumed all lists contain the same number of entries and that it matches the length of *category_names*. category_names : list of str The category labels. """ labels = list(results.keys()) data = np.array(list(results.values())) data_cum = data.cumsum(axis=1) category_colors = plt.get_cmap('RdYlGn')( np.linspace(0.15, 0.85, data.shape[1])) fig, ax = plt.subplots(figsize=(9.2, 5)) ax.invert_yaxis() ax.xaxis.set_visible(False) ax.set_xlim(0, np.sum(data, axis=1).max()) for i, (colname, color) in enumerate(zip(category_names, category_colors)): widths = data[:, i] starts = data_cum[:, i] - widths ax.barh(labels, widths, left=starts, height=0.5, label=colname, color=color) xcenters = starts + widths / 2 r, g, b, _ = color text_color = 'white' if r * g * b < 0.5 else 'darkgrey' for y, (x, c) in enumerate(zip(xcenters, widths)): ax.text(x, y, str(int(c)), ha='center', va='center', color=text_color) ax.legend(ncol=len(category_names), bbox_to_anchor=(0, 1), loc='lower left', fontsize='small') return fig, ax survey(results, category_names) plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
多层圆环图

import matplotlib.pyplot as plt plt.rcParams['font.sans-serif']=['KaiTi'] plt.rcParams['axes.unicode_minus']=False group_names=['吉祥物(73%)', '其他(3%)', '校花(16%)', '校树(8%)'] group_size=[2585,95,563,301] subgroup_names=['', '','学生','', '','学生','', '','学生','', '','学生'] subgroup_size=[221 ,36, 2328,34, 2 ,59,56, 8 ,499,62 ,7, 232] # Create colors # 设置颜色 a, b, c,d=['#41555d','#646464','#969696','#DDDDDD'] # First Ring (outside) # 外圈 fig, ax = plt.subplots() # 设置等比例轴,x和y轴等比例 ax.axis('equal') # 画饼图 mypie, _ = ax.pie(group_size, radius=1.3, labels=group_names, textprops={'fontsize': 12},colors=[a, b, c,d],wedgeprops=dict(width=0.3, edgecolor='white')); # Second Ring (Inside) # 画第二个圆 mypie2, _ = ax.pie(subgroup_size, radius=1.3-0.3, labels=subgroup_names,textprops={'fontsize': 11}, labeldistance=0.7, colors=['#e9f1f6', '#e3f9fd','#a1afc9','#e9f1f6', '#e3f9fd','#FFCC99','#e9f1f6', '#e3f9fd','#c0ebd7','#e9f1f6', '#e3f9fd','#edd1d8'],wedgeprops=dict(width=0.6, edgecolor='white')); # ax.labels() plt.margins(0,0);
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
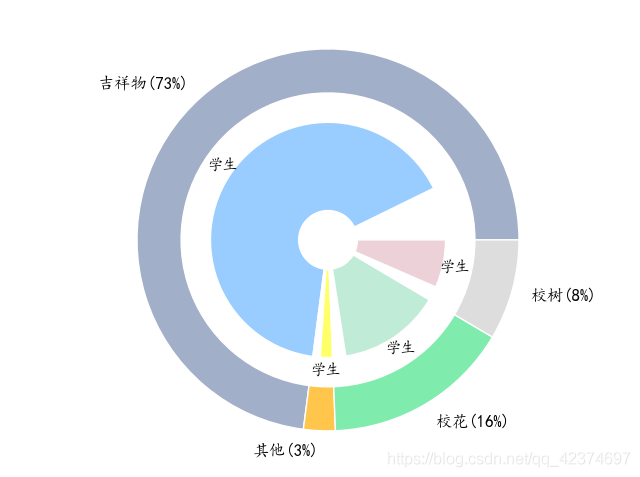
import matplotlib.pyplot as plt plt.rcParams['font.sans-serif']=['KaiTi'] plt.rcParams['axes.unicode_minus']=False group_names=['吉祥物(73%)', '其他(3%)', '校花(16%)', '校树(8%)'] group_size=[2585,95,563,301] subgroup_names=['', '','学生','', '','学生','', '','学生','', '','学生'] subgroup_size=[221 ,36, 2328,34, 2 ,59,56, 8 ,499,62 ,7, 232] # Create colors # 设置颜色 a, b, c,d=['#a1afc9','#ffc64b','#7fecad','#DDDDDD'] # First Ring (outside) # 外圈 fig, ax = plt.subplots() # 设置等比例轴,x和y轴等比例 ax.axis('equal') # 画饼图 mypie, _ = ax.pie(group_size, radius=1.3, labels=group_names, textprops={'fontsize': 12},colors=[a, b, c,d],wedgeprops=dict(width=0.3, edgecolor='white')); # Second Ring (Inside) # 画第二个圆 mypie2, _ = ax.pie(subgroup_size, radius=1.3-0.5, labels=subgroup_names,textprops = dict(rotation_mode = 'anchor', fontsize= 11, va='center', ha='center'), colors=['#FFFFFF', '#FFFFFF','#99CCFF','#FFFFFF', '#FFFFFF','#FFFF66','#FFFFFF', '#FFFFFF','#c0ebd7','#FFFFFF', '#FFFFFF','#edd1d8'],wedgeprops=dict(width=0.6, edgecolor='white')); # ax.labels() plt.margins(0,0);
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
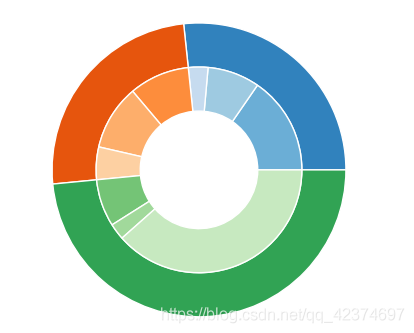
import matplotlib.pyplot as plt import numpy as np fig, ax = plt.subplots() size = 0.3 vals = np.array([[60., 32.,12], [37., 40.,20], [29., 10.,30]]) # cmap参数接受一个值(每个值代表一种配色方案),并将该值对应的颜色图分配给当前图窗。 cmap = plt.get_cmap("tab20c") outer_colors = cmap(np.arange(3)*4) inner_colors = cmap(np.array([1, 2,3, 5, 6,7, 9, 10,11])) ax.pie(vals.sum(axis=1), radius=1, colors=outer_colors, wedgeprops=dict(width=size, edgecolor='w')) ax.pie(vals.flatten(), radius=1-size, colors=inner_colors, wedgeprops=dict(width=size, edgecolor='w')) ax.set(aspect="equal", title='Pie plot with `ax.pie`') plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
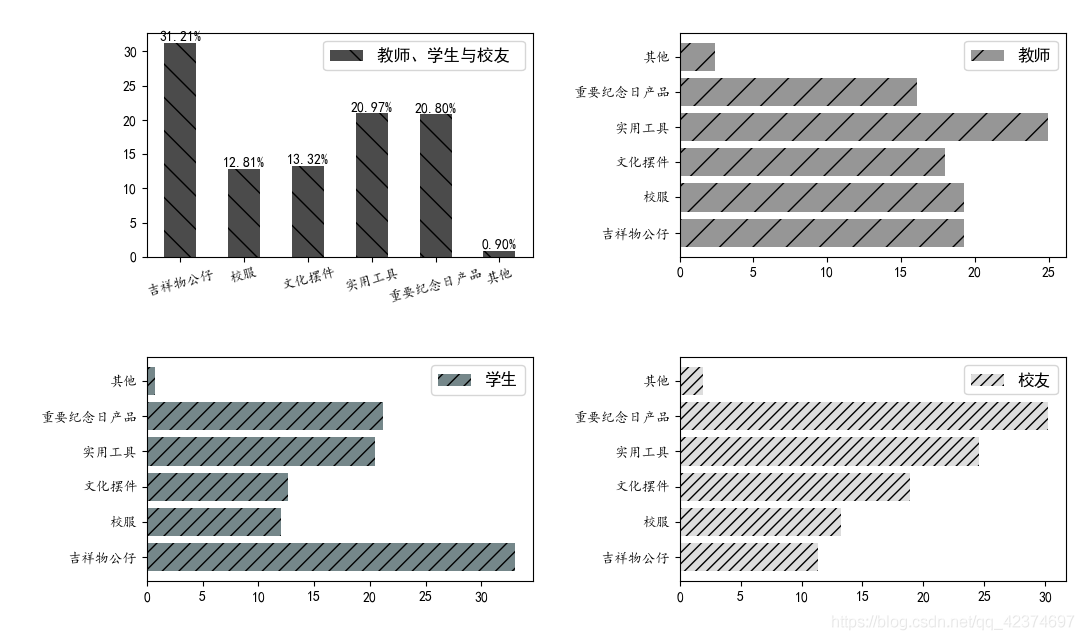
import numpy as np import matplotlib.pyplot as plt y = [31.21,12.81,13.32,20.97,20.8,0.9] y1 = [19.3,19.3,17.96,24.93,16.09,2.41] y2 = [32.97,12.03,12.67,20.43,21.2,0.71] y3= [11.32,13.21,18.87,24.53,30.19,1.89] font = {'family':'simhei',#这里必须要有第12行的操作前提 'weight': 'normal', 'size': 12, }; index=np.arange(len(y)); #x = ['REST','LAPT','AUTO'] x = ['吉祥物公仔','校服','文化摆件','实用工具','重要纪念日产品','其他'] #总共有几组,就设置成几,我们这里有三组,所以设置为3 fig,axes=plt.subplots(nrows=2,ncols=2,figsize=(9,4)) plt.subplot(2,2,1) plt.bar(x, y,label='教师、学生与校友 ',color='#4B4B4B',hatch='\\',width=0.5) plt.xticks(rotation=15) plt.legend(loc = "best",prop=font,labelspacing=1) for a,b in zip(index,y): #柱子上的数字显示 plt.text(a,b,'%.2f'%b + '%',ha='center',va='bottom',fontsize=10); # plt.tight_layout() plt.subplot(2,2,2) plt.barh(x, y1, color = "#969696",label='教师',hatch="/") plt.legend(loc = "best",prop=font,labelspacing=1) # plt.tight_layout() plt.subplot(2,2,3) plt.barh(x, y2, color = "#75878a",label='学生',hatch="//") plt.legend(loc = "best",prop=font,labelspacing=1) plt.tight_layout() plt.subplot(2,2,4) plt.barh(x, y3, color = "#DDDDDD",label='校友',hatch="///") plt.legend(loc = "best",prop=font,labelspacing=1) plt.tight_layout() plt.show() plt.savefig(r'C:\Users\Administrator\Desktop\ig_cat.jpg', dpi=500) #指定分辨率保存
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
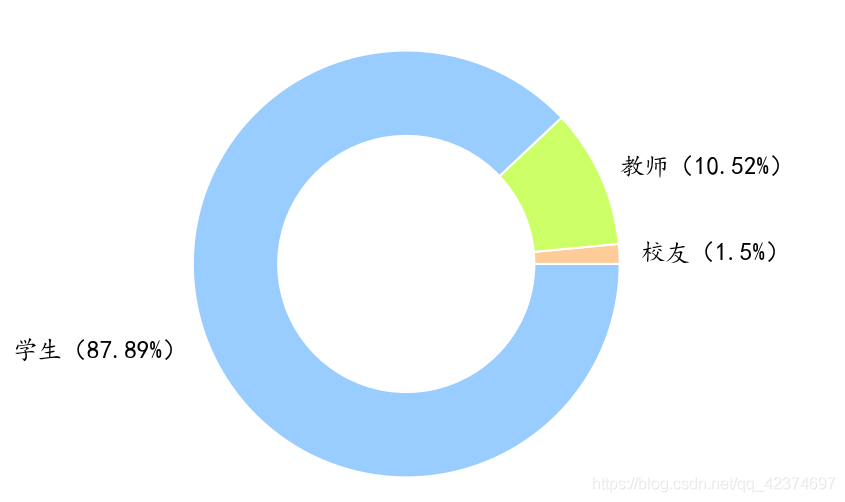
import numpy as np
import matplotlib.pyplot as plt
plt.figure(figsize=(6,5),dpi=150)
x1=np.array([1.5,10.52,87.89])
labels=["校友(1.5%)","教师(10.52%)","学生(87.89%)"]
plt.rcParams['font.sans-serif']=['KaiTi']
plt.rcParams['axes.unicode_minus']=False
plt.pie(x1,labels=labels,radius=1.0,
wedgeprops=dict(width=0.4,edgecolor='w'), textprops={'fontsize': 12},colors=['#FFCC99','#CCFF66','#99CCFF'])
plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
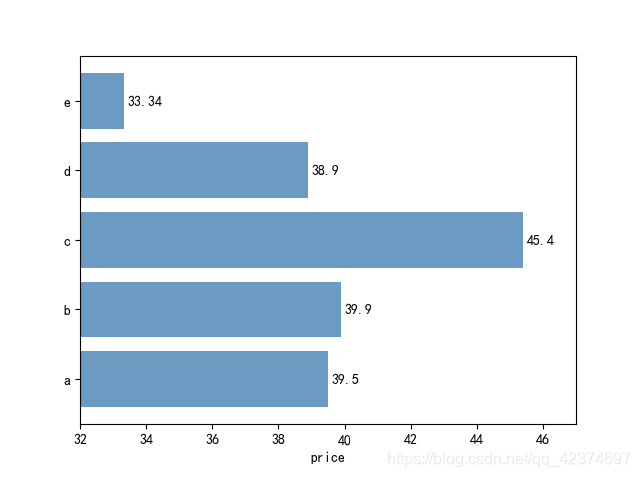
# 导入绘图模块 import matplotlib.pyplot as plt # 构建数据 price = [39.5, 39.9, 45.4, 38.9, 33.34] # 绘图 plt.barh(range(5), price, align='center', color='steelblue', alpha=0.8) # 添加轴标签 plt.xlabel('price') # 添加标题 # plt.title('Books at different prices') # 添加刻度标签 plt.yticks(range(5), ['a', 'b', 'c', 'd', 'e']) # 设置Y轴的刻度范围 plt.xlim([32, 47]) # 为每个条形图添加数值标签 for x, y in enumerate(price): plt.text(y + 0.1, x, '%s' % y, va='center') plt.savefig('foo.png') # 显示图形 plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20

import pandas as pd import numpy as np import seaborn as sns import matplotlib.pyplot as plt import seaborn as sns sns.set(style="whitegrid") df =pd.read_clipboard() df plt.rcParams['font.sans-serif'] = ['SimHei'] #用来显示中文标签 plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号 plt.rcParams['savefig.dpi'] = 100 # 图片像素 plt.rcParams['figure.dpi'] = 100 # 分辨率 x = df.index fig,axes=plt.subplots(nrows=1,ncols=3,figsize=(10,6)) plt.subplot(1,3,1) sns.barplot(x,df['总的'],palette=sns.hls_palette(8 , l = .8, s = .5)) plt.xticks([]) # 不显示x轴 plt.ylabel('教师、学生与校友', fontsize=10) plt.yticks([]) # 不显示y轴 # plt.title('教师、学生与校友') plt.subplot(1.3,2) sns.barplot(x,df['学生'],palette=sns.light_palette('red',reverse=False)) plt.xticks([]) # 不显示x轴 plt.ylabel('学生') plt.yticks([]) # 不显示y轴 plt.subplot(1,3,3) sns.barplot(x,df['教师'],palette=sns.color_palette('Greens')) plt.xticks([]) # 不显示x轴 plt.ylabel('教师') plt.yticks([]) # 不显示y轴 plt.subplot(4,1,4) sns.barplot(x,df['校友'],palette=sns.color_palette('Blues')) plt.xticks(rotation=14) # 不显示x轴 plt.ylabel('校友') plt.yticks([]) # 不显示y轴 plt.tick_params(labelsize=8) plt.savefig(r'C:\Users\Administrator\Desktop\2fig_cat.jpg', dpi=500) #指定分辨率保存
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
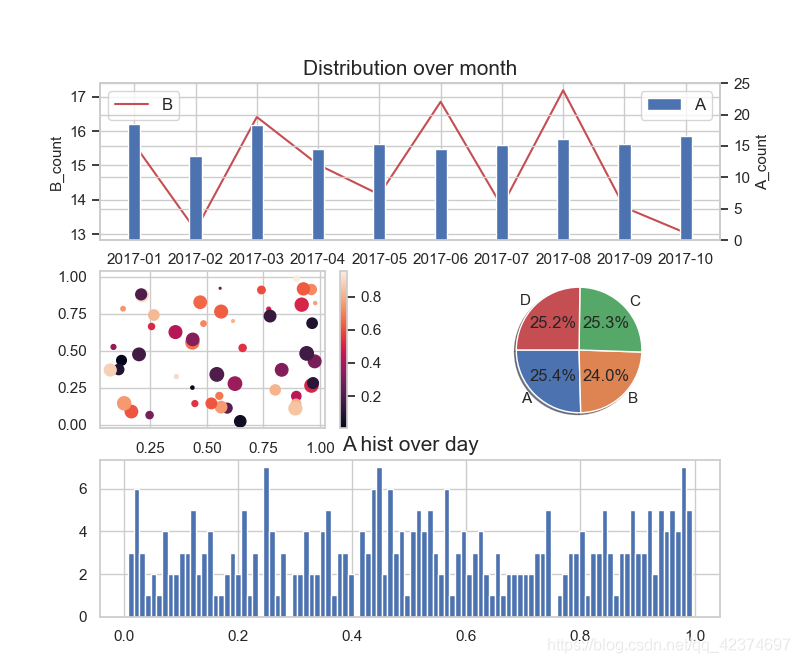
import pandas as pd import time import numpy as np from matplotlib import pyplot as plt dates = pd.date_range('20170101', periods=300) df = pd.DataFrame(np.random.rand(300,4), index=dates, columns=list('ABCD')) # ///按月份对商品数据求和 date_groupby = df.groupby(lambda x:pd.datetime.strftime(x,'%Y-%m')).apply(sum) # ///统计四种商品的出货总量占比 date_sum = df.apply(sum) date_ratio = date_sum/date_sum.sum() fig = plt.figure(figsize=(8,9)) ax_0 = fig.add_subplot(3, 1, 1 ) ax_0_twin = ax_0.twinx() ax_0_twin.bar(date_groupby.index,date_groupby["A"],width = 0.2,label = "A") plt.ylim((0, 25)) ax_0.plot(date_groupby.index,date_groupby["B"],color = "r", label = "B") ax_0_twin.set_title(r'Distribution over month',fontsize=15) ax_0.legend(loc=2, prop={'size': 12}) ax_0_twin.legend(loc=1, prop={'size': 12}) ax_0.set_ylabel(r'B_count',fontsize=11) ax_0_twin.set_ylabel(r'A_count',fontsize=11) ax_1 = fig.add_subplot(3, 2, 3 ) rng = np.random.RandomState(10) colors = rng.rand(50) sc = ax_1.scatter(df["A"].iloc[0:50],df["B"].iloc[0:50], c=colors,s=100*df["C"].iloc[0:50]) plt.colorbar(sc) ax_2 = fig.add_subplot(3, 2, 4 ) ax_2.pie(date_ratio, labels=date_ratio.index , autopct = '%3.1f%%', startangle = 180, shadow = True) ax_3 = fig.add_subplot(3, 1, 3 ) ax_3.hist(df["A"],bins = 100) ax_3.set_title(r'A hist over day',fontsize=15)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
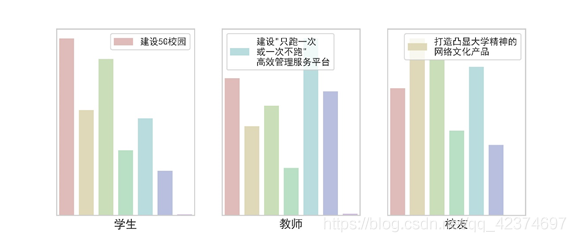
import pandas as pd import numpy as np import seaborn as sns import matplotlib.pyplot as plt import seaborn as sns import matplotlib.patches as mpatches sns.set(style="whitegrid") df =pd.read_clipboard() df plt.rcParams['font.sans-serif'] = ['SimHei'] #用来显示中文标签 plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号 x = df.index fig,axes=plt.subplots(nrows=1,ncols=3,figsize=(6,4)) plt.subplot(1,3,1) sns.barplot(x,df['学生'],palette=sns.hls_palette(8 , l = .8, s = .5)) plt.xticks([]) # 不显示x轴 plt.xlabel('学生', fontsize=14) plt.yticks([]) # 不显示y轴 plt.ylabel(' ') ax=plt.gca() box = ax.get_position() ax.set_position([box.x0, box.y0, box.width , box.height]) patches=[mpatches.Patch(color='#DFBBB9', label='建设5G校园')] ax.legend(handles=patches, bbox_to_anchor=(1,1)) #生成legend plt.subplot(1,3,2) sns.barplot(x,df['教师'],palette=sns.hls_palette(8 , l = .8, s = .5)) plt.xticks([]) # 不显示x轴 plt.xlabel('教师', fontsize=14) plt.yticks([]) # 不显示y轴 plt.ylabel(' ') ax=plt.gca() box = ax.get_position() ax.set_position([box.x0, box.y0, box.width , box.height]) patches=[mpatches.Patch(color='#B9DDDF', label='建设"只跑一次\n或一次不跑"\n高效管理服务平台')] ax.legend(handles=patches,loc=2) #生成legend plt.subplot(1,3,3) sns.barplot(x,df['校友'],palette=sns.hls_palette(8 , l = .8, s = .5)) plt.xticks([]) # 不显示x轴 plt.xlabel('校友', fontsize=14) plt.yticks([]) # 不显示y轴 plt.ylabel(' ') ax=plt.gca() box = ax.get_position() ax.set_position([box.x0, box.y0, box.width , box.height]) patches=[mpatches.Patch(color='#DFD8B9', label='打造凸显大学精神的\n网络文化产品')] ax.legend(handles=patches,loc=1) #生成legend plt.savefig(r'C:\Users\Administrator\Desktop\2fig_cat.jpg', dpi=500) #指定分辨率保存
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
相关系数热力图
import plotly.figure_factory as ff
corrs = df.corr()
figure = ff.create_annotated_heatmap(z=corrs.values,x=list(corrs.columns),y=list(corrs.index), annotation_text=corrs.round(2).values, showscale=True)
- 1
- 2
- 3
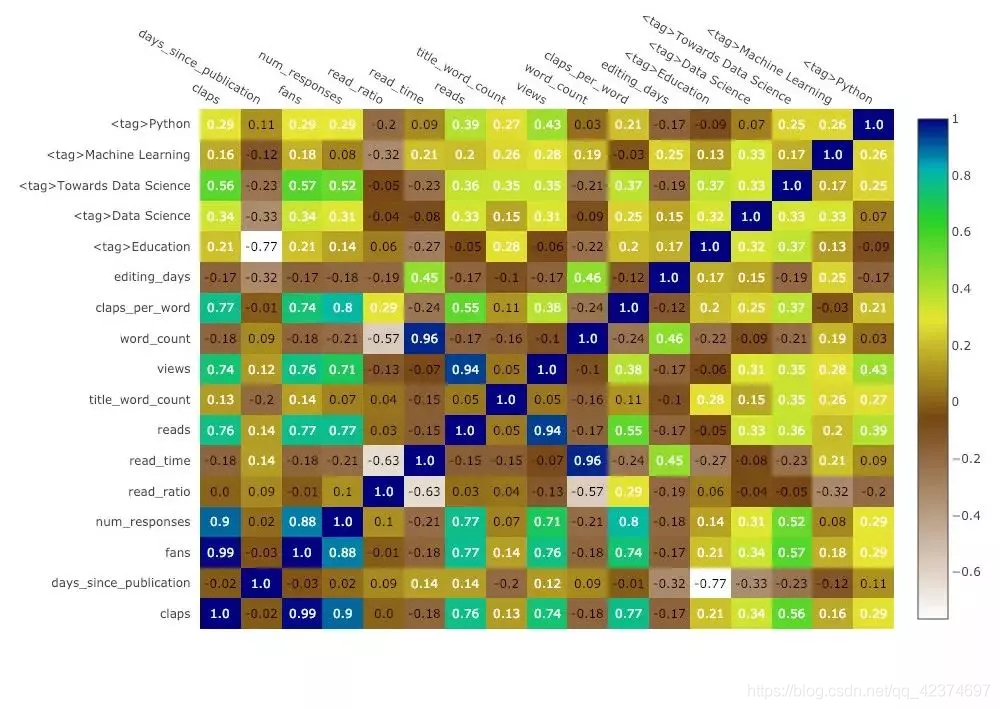
// 指定图表的配置项和数据 var option = { tooltip: { trigger: 'item', formatter: "{a} <br/>{b}: {c} ({d}%)" }, color:["#27D9C8","#D8D8D8"], title:{ text:"80%", left:"center", top:"50%", textStyle:{ color:"#27D9C8", fontSize:36, align:"center" } }, graphic:{ type:"text", left:"center", top:"40%", style:{ text:"运动达标率", textAlign:"center", fill:"#333", fontSize:20, fontWeight:700 } }, series: [ { name: '运动情况', type: 'pie', radius: ['65%', '70%'], avoidLabelOverlap: false, label: { normal: { show: false, position: 'center' }, }, data: [ { value: 80, name: '已完成' }, { value: 20, name: '未完成' }, ] } ] };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
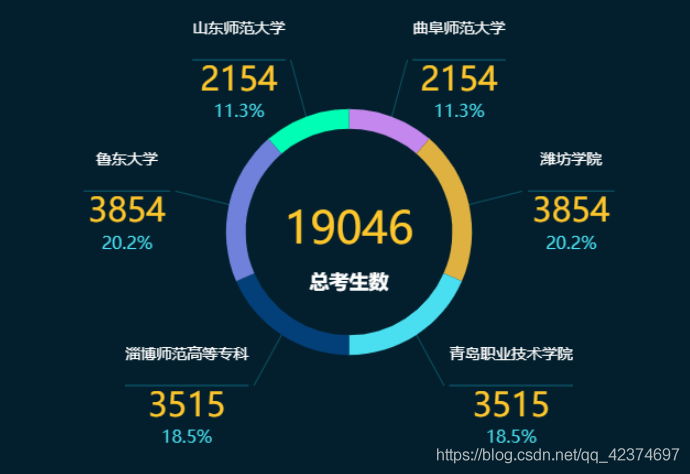
var scale = 1; var echartData = [{ value: 2154, name: '曲阜师范大学' }, { value: 3854, name: '潍坊学院' }, { value: 3515, name: '青岛职业技术学院' }, { value: 3515, name: '淄博师范高等专科' }, { value: 3854, name: '鲁东大学' }, { value: 2154, name: '山东师范大学' }] var rich = { yellow: { color: "#ffc72b", fontSize: 30 * scale, padding: [5, 4], align: 'center' }, total: { color: "#ffc72b", fontSize: 40 * scale, align: 'center' }, white: { color: "#fff", align: 'center', fontSize: 14 * scale, padding: [21, 0] }, blue: { color: '#49dff0', fontSize: 16 * scale, align: 'center' }, hr: { borderColor: '#0b5263', width: '100%', borderWidth: 1, height: 0, } } option = { backgroundColor: '#031f2d', title: { text:'总考生数', left:'center', top:'53%', padding:[24,0], textStyle:{ color:'#fff', fontSize:18*scale, align:'center' } }, legend: { selectedMode:false, formatter: function(name) { var total = 0; //各科正确率总和 var averagePercent; //综合正确率 echartData.forEach(function(value, index, array) { total += value.value; }); return '{total|' + total + '}'; }, data: [echartData[0].name], // data: ['高等教育学'], // itemGap: 50, left: 'center', top: 'center', icon: 'none', align:'center', textStyle: { color: "#fff", fontSize: 16 * scale, rich: rich }, }, series: [{ name: '总考生数量', type: 'pie', radius: ['42%', '50%'], hoverAnimation: false, color: ['#c487ee', '#deb140', '#49dff0', '#034079', '#6f81da', '#00ffb4'], label: { normal: { formatter: function(params, ticket, callback) { var total = 0; //考生总数量 var percent = 0; //考生占比 echartData.forEach(function(value, index, array) { total += value.value; }); percent = ((params.value / total) * 100).toFixed(1); return '{white|' + params.name + '}\n{hr|}\n{yellow|' + params.value + '}\n{blue|' + percent + '%}'; }, rich: rich }, }, labelLine: { normal: { length: 55 * scale, length2: 0, lineStyle: { color: '#0b5263' } } }, data: echartData }] };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
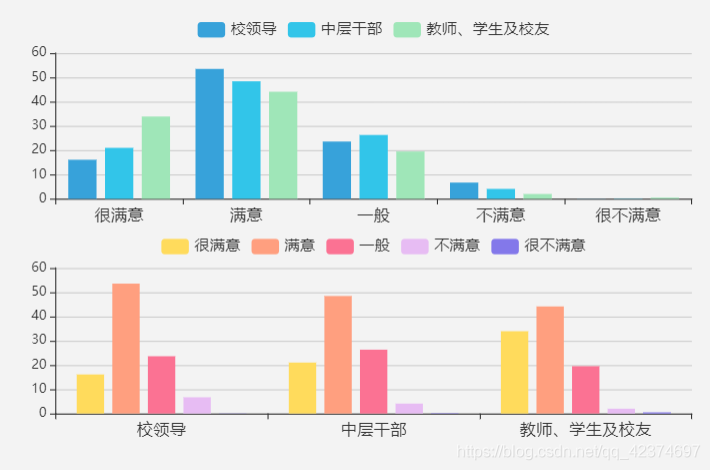
option = { toolbox: { show: true, feature: { dataView: {show:true}, saveAsImage: { //excludeComponents :['toolbox'], pixelRatio: 20 } } }, legend: [{ data: ['校领导', '中层干部', '教师、学生及校友'], icon: "roundRect", x:'center', y:'6%', textStyle: { //图例文字的样式 fontSize: 14 }, },{ data: ['很满意', '满意', '一般', '不满意','很不满意'], icon: "roundRect", x:'center', y:'50%', textStyle: { //图例文字的样式 fontSize: 14 }, }], tooltip: {}, dataset: { source: [ ['product', '很满意', '满意', '一般', '不满意','很不满意'], ['校领导', 16.1, 53.5, 23.6, 6.7,0.1], ['中层干部', 21, 48.4, 26.3, 4.1,0.2], ['教师、学生及校友', 33.9, 44.1, 19.5, 2,0.5] ] }, xAxis: [ {type: 'category', gridIndex: 0,axisLabel: { fontSize: 15 }}, {type: 'category', gridIndex: 1,axisLabel: { fontSize: 15 }}, ], yAxis: [ {gridIndex: 0}, {gridIndex: 1} ], grid: [ {bottom: '57%'}, {top: '57%'} ], series: [ // These series are in the first grid. {type: 'bar', seriesLayoutBy: 'row'}, {type: 'bar', seriesLayoutBy: 'row'}, {type: 'bar', seriesLayoutBy: 'row'}, // These series are in the second grid. {type: 'bar', xAxisIndex: 1, yAxisIndex: 1}, {type: 'bar', xAxisIndex: 1, yAxisIndex: 1}, {type: 'bar', xAxisIndex: 1, yAxisIndex: 1}, {type: 'bar', xAxisIndex: 1, yAxisIndex: 1}, {type: 'bar', xAxisIndex: 1, yAxisIndex: 1} ] };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
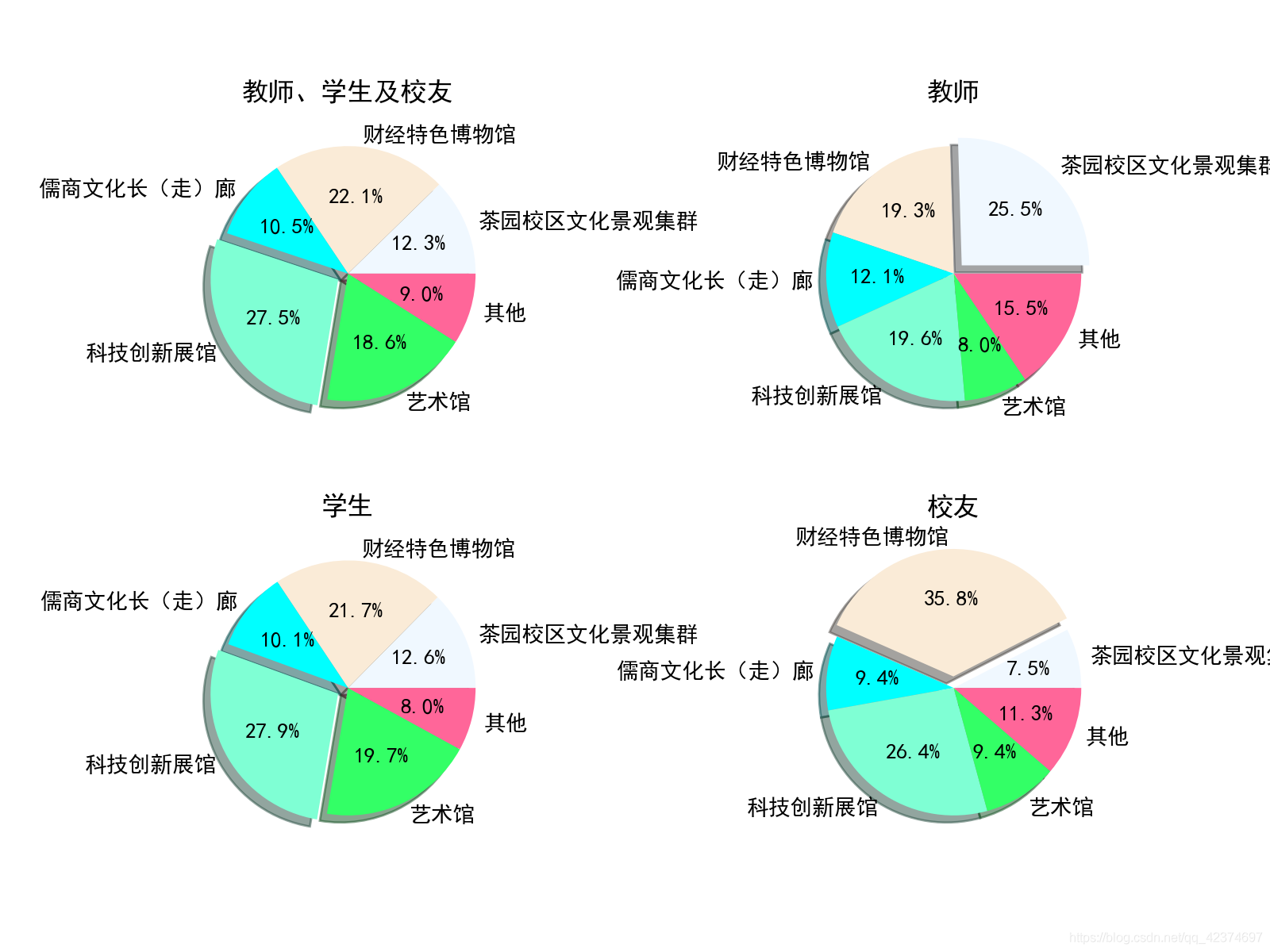
import pandas as pd #导入数据分析模块 import numpy as np import matplotlib.pyplot as plt #导入绘图模块 plt.rcParams['font.sans-serif']='SimHei' data=pd.read_excel(r"C:\Users\Administrator\Desktop\数据.xlsx",index_col='身份') #读取数据 row_sum=data.sum(axis=1).apply(float) #按行求和 partion_data=data.div(row_sum,axis=0) #计算行百分比 rows,cols=data.shape #数据尺寸 fig,ax=plt.subplots(nrows=2,ncols=2,figsize=(8, 6)) #建立饼图坑 axes=ax.flatten() #将坑位展平 labels_=list(data.columns)#设置标签 colors_=["aliceblue","antiquewhite","aqua","aquamarine",'#33FF66','#FF6699'] #设置饼图配色 for row in range(rows): explode=[0, 0, 0, 0,0,0] #初始化突出位置 explode[labels_.index(partion_data.iloc[row,:].idxmax())]=0.09 #新的突出切片 axes[row].pie(partion_data.iloc[row,:],autopct='%1.1f%%',labels=labels_,colors=colors_, explode=explode,shadow=True) #绘制子饼图 axes[row].set_title(data.index[row]) #设置标题 plt.subplots_adjust(left=None, bottom=None, right=None, top=None,wspace=0.6, hspace=0.3) #调整子图间距 plt.savefig(r"C:\Users\Administrator\Desktop\pie.png",dpi=200) #保存图片
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
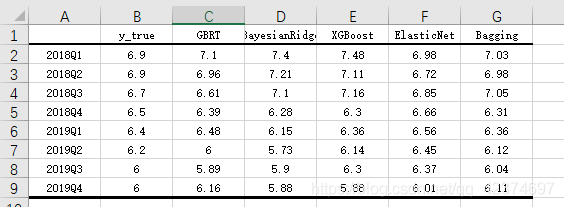
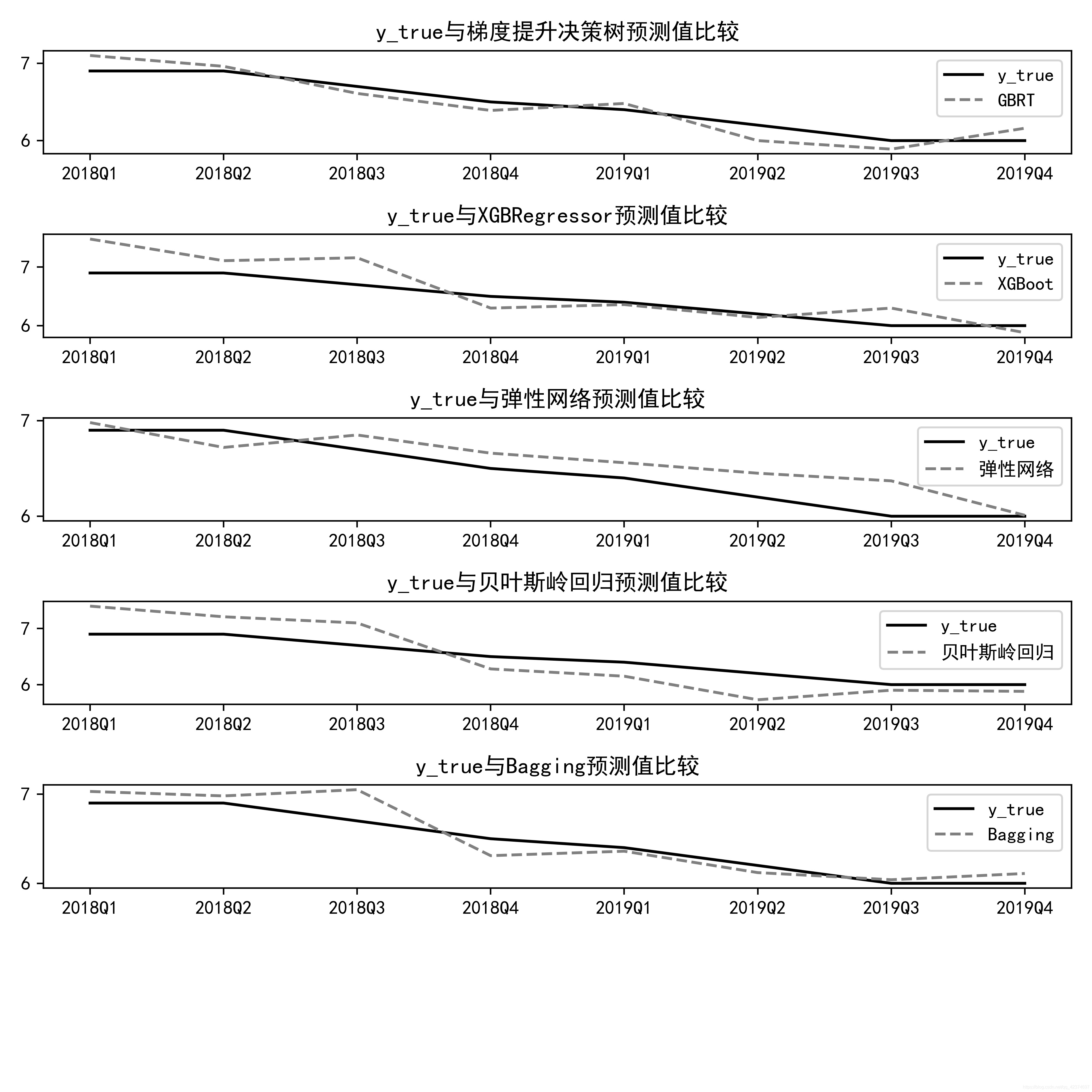
a = pd.read_excel('C:\\Users\\Administrator\\Desktop\\a.xlsx') plt.figure(figsize=(8,8)) plt.subplot(611) plt.plot(a['y_true'],color='#000000',label='y_true') plt.plot(a['GBRT'],linestyle='--',color='#808080',label='GBRT') plt.title('y_true与梯度提升决策树预测值比较') plt.xticks(range(8),a.iloc[:,0].tolist()) plt.legend(loc=1, prop={'size': 10}) # plt.subplots_adjust(hspace=0.9) plt.tight_layout() plt.subplot(612) plt.plot(a['y_true'],color='#000000',label='y_true') plt.plot(a['XGBoost'],linestyle='--',color='#808080',label='XGBoot') plt.title('y_true与XGBRegressor预测值比较') plt.xticks(range(8),a.iloc[:,0].tolist()) plt.subplots_adjust(left=None, bottom=0.2, right=None, top=0.5, wspace=None, hspace=None) plt.legend(loc=1, prop={'size': 10}) plt.tight_layout() plt.subplot(613) plt.plot(a['y_true'],color='#000000',label='y_true') plt.plot(a['ElasticNet'],linestyle='--',color='#808080',label='弹性网络') plt.title('y_true与弹性网络预测值比较') plt.xticks(range(8),a.iloc[:,0].tolist()) plt.legend(loc=1, prop={'size': 10}) plt.tight_layout() plt.subplot(614) plt.plot(a['y_true'],color='#000000',label='y_true') plt.plot(a['BayesianRidge'],linestyle='--',color='#808080',label='贝叶斯岭回归') plt.title('y_true与贝叶斯岭回归预测值比较') plt.xticks(range(8),a.iloc[:,0].tolist()) plt.legend(loc=1, prop={'size': 10}) plt.tight_layout() plt.subplot(615) plt.plot(a['y_true'],color='#000000',label='y_true') plt.plot(a['Bagging'],linestyle='--',color='#808080',label='Bagging') plt.title('y_true与Bagging预测值比较') plt.xticks(range(8),a.iloc[:,0].tolist()) plt.legend(loc=1, prop={'size': 10}) plt.tight_layout() plt.savefig(r'C:\Users\Administrator\Desktop\2fig_cat.jpg', dpi=500) #指定分辨率保存
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
.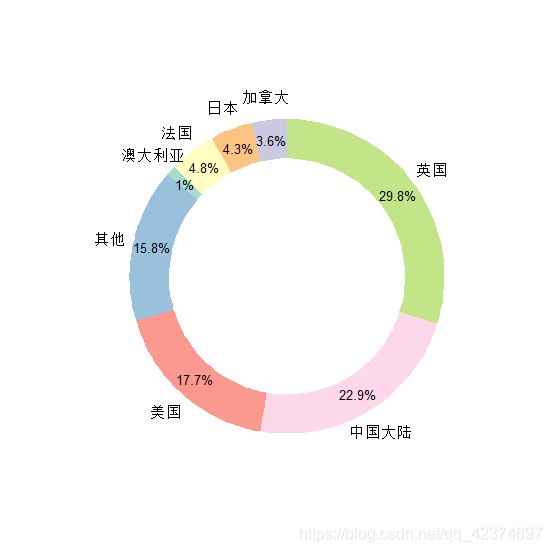
library(tidyverse) library(ggthemes) coutry<-c('英国','中国大陆','美国','其他','澳大利亚','法国','日本','加拿大') rate<-c(29.8,22.9,17.7,15.8,1,4.8,4.3,3.6) rate_per<-paste(as.character(rate),'%',sep='') ad<-data.frame(type=coutry,n=rate,rate_per=rate_per) #ad = data.frame(type = c("Poster", "Billboard", "Bus", "Digital"),n = c(529, 356, 59, 81)) ad$fraction = ad$n / sum(ad$n) ad$ymax = cumsum(ad$fraction) ad$ymin = c(0, head(ad$ymax, n = -1)) p<-ggplot(data = ad, aes(fill = type, ymax = ymax, ymin = ymin, xmax = 4, xmin = 3)) + geom_rect(show.legend = F,alpha=0.8) + scale_fill_brewer(palette = 'Set3')+ coord_polar(theta = "y") + labs(x = "", y = "", title = "",fill='地区') + xlim(c(0, 5)) + theme_light() + theme(panel.grid=element_blank()) + ## 去掉白色外框 theme(axis.text=element_blank()) + ## 把图旁边的标签去掉 theme(axis.ticks=element_blank()) + ## 去掉左上角的坐标刻度线 theme(panel.border=element_blank()) + ## 去掉最外层的正方形边框 geom_text(aes(x = 4.6, y = ((ymin+ymax)/2),label = type) ,size=4)+ geom_text(aes(x = 3.5, y = ((ymin+ymax)/2),label = rate_per) ,size=3.6) ggsave('环形.png')
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
分布图
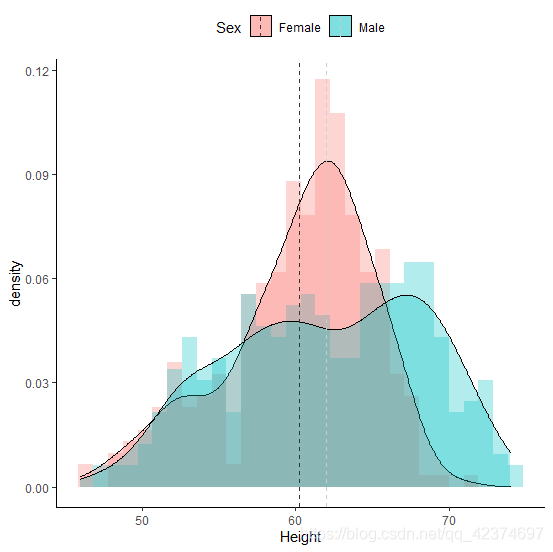
library(ggplot2) library(plyr) set.seed(1234) df = read.table('儿童呼吸道疾病.txt',header=T) head(df) mu <- ddply(df, 'Sex', summarise, grp.mean=mean(Height)) ggplot(df, aes(x=Height, fill=Sex)) + geom_histogram(aes(y=..density..), alpha=0.3,position='identity') + geom_density(alpha=0.3) + geom_vline(data=mu, aes(xintercept=grp.mean,color=Sex),linetype='dashed') + scale_color_grey() + theme_classic()+ theme(legend.position='top')
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16

# Data data <- data.frame( name = c("DD","with himself","with DC","with Silur" ,"DC","with himself","with DD","with Silur" ,"Silur","with himself","with DD","with DC" ), average = sample(seq(1,10) , 12 , replace=T), number = sample(seq(4,39) , 12 , replace=T) ) # Increase bottom margin par(mar=c(6,4,4,4)) # Basic Barplot my_bar <- barplot(data$average , border=F , names.arg=data$name , las=2 , col=c(rgb(0.3,0.1,0.4,0.6) , rgb(0.3,0.5,0.4,0.6) , rgb(0.3,0.9,0.4,0.6) , rgb(0.3,0.9,0.4,0.6)) , ylim=c(0,13) , main="" ) # Add abline abline(v=c(4.9 , 9.7) , col="grey") # Add the text text(my_bar, data$average+0.4 , paste("n: ", data$number, sep="") ,cex=1) #Legende legend("topleft", legend = c("Alone","with Himself","With other genotype" ) , col = c(rgb(0.3,0.1,0.4,0.6) , rgb(0.3,0.5,0.4,0.6) , rgb(0.3,0.9,0.4,0.6) , rgb(0.3,0.9,0.4,0.6)) , bty = "n", pch=20 , pt.cex = 2, cex = 0.8, horiz = FALSE, inset = c(0.05, 0.05))
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
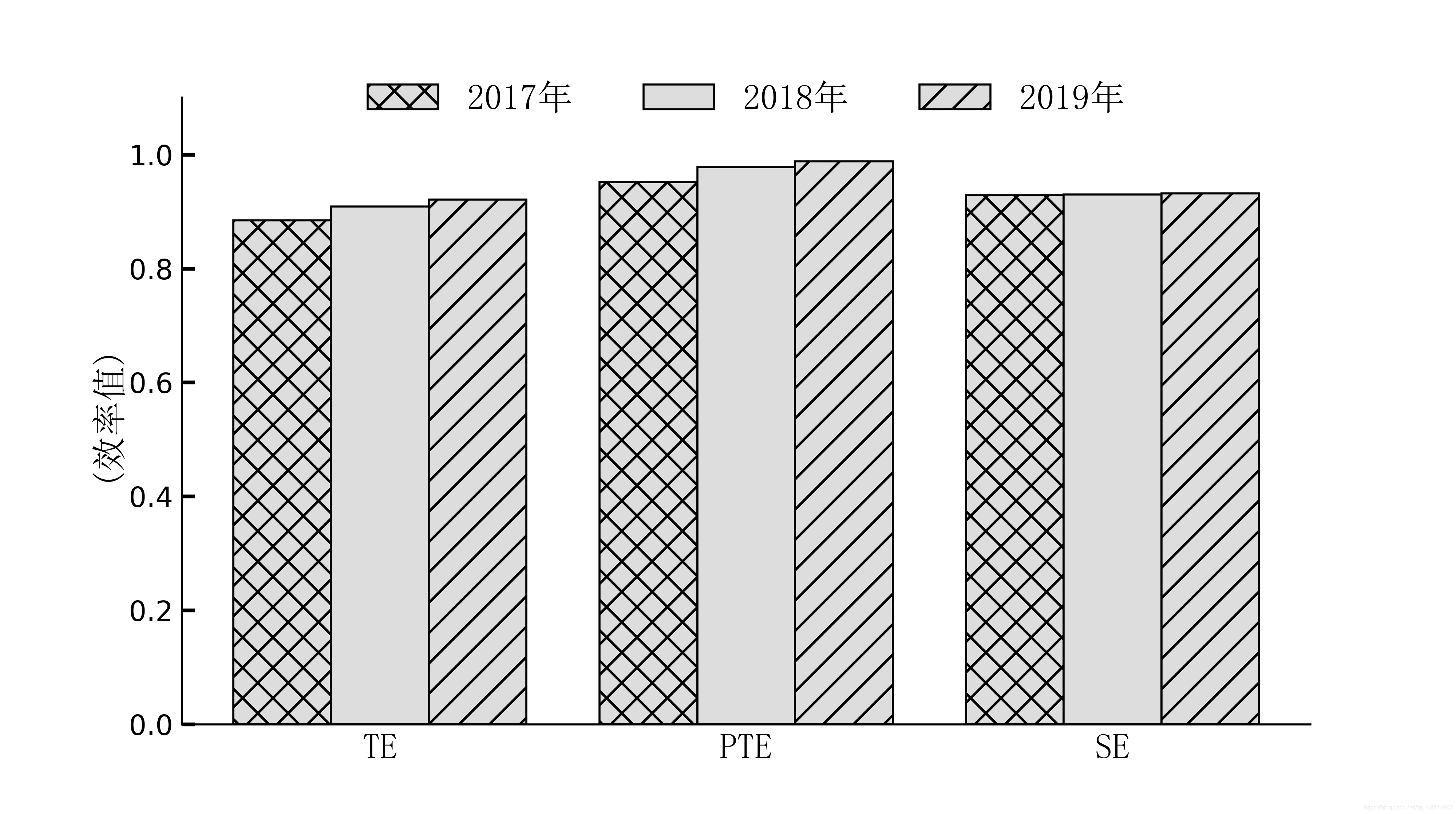
# -*- coding: utf-8 -*- """ Created on Thu Dec 17 22:12:50 2020 @author: Administrator """ import matplotlib.pyplot as plt import pandas as pd import numpy as np labels = ['TE','PTE','SE'] y1 = [0.885,0.952,0.929] y2 = [0.909,0.978,0.930] y3= [0.921,0.988,0.932] fig,ax = plt.subplots(1,1,figsize=(8,4.5)) x = np.arange(len(labels)) total_width, n = 0.8, 3 width = total_width / n x = x - (total_width - width) / 2 label_font = { 'weight':'bold', 'size':14, 'family':'simsun' } colors = ['#9999FF','#58C9B9','#CC33CC','#D1B6E1','#99FF99','#C0C0C0'] rects1 = ax.bar(x, y1, width, label='2017年',ec='k',color='#DDDDDD',lw=.8, hatch='xx') rects2 = ax.bar(x + width, y2, width, label='2018年',ec='k',color='#DDDDDD', lw=.8,hatch='') rects3 = ax.bar(x + width * 2, y3, width, label='2019年',ec='k',color='#DDDDDD', lw=.8,hatch='//') # tick_params参数刻度线样式设置 # ax.tick_params(axis=‘x’, tickdir=‘in’, labelrotation=20)参数详解 # axis : 可选{‘x’, ‘y’, ‘both’} ,选择对哪个轴操作,默认是’both’ # which : 可选{‘major’, ‘minor’, ‘both’} 选择对主or副坐标轴进行操作 # direction/tickdir : 可选{‘in’, ‘out’, ‘inout’}刻度线的方向 # color : 刻度线的颜色,我一般用16进制字符串表示,eg:’#EE6363’ # width : float, 刻度线的宽度 # size/length : float, 刻度线的长度 # pad : float, 刻度线与刻度值之间的距离 # labelsize : float/str, 刻度值字体大小 # labelcolor : 刻度值颜色 # colors : 同时设置刻度线和刻度值的颜色 # bottom, top, left, right : bool, 分别表示上下左右四边,是否显示刻度线,True为显示 ax.tick_params(which='major',direction='in',length=5,width=1.5,labelsize=11,bottom=False) ax.tick_params(axis='x',labelsize=11,bottom=False,labelrotation=0) ax.set_xticks(range(len(labels))) # ax.set_yticks([0,0.2,0.4,0.6,0.8,1]) ax.set_ylim(ymin = 0,ymax = 1.1) # 0 - 1800 ,200为一个间距 ax.set_yticks(np.arange(0,1.1,0.2)) ax.set_ylabel('(效率值)',fontdict=label_font) ax.set_xticklabels(labels,fontdict=label_font) ax.legend(prop =label_font,loc='center', bbox_to_anchor=(0.5,1),ncol=4,frameon=False,shadow=False) ''' # 设置有边框和头部边框颜色为空right、top、bottom、left ax.spines['right'].set_color('none') ax.spines['top'].set_color('none') ''' ax.spines['right'].set_visible(False) ax.spines['top'].set_visible(False) # # 上下左右边框线宽 # linewidth = 2 # for spine in ['top','bottom','left','right']: # ax.spines[spine].set_linewidth(linewidth) # Add some text for labels, title and custom x-axis tick labels, etc. # def autolabel(rects): # for rect in rects: # height = rect.get_height() # ax.annotate('{}'.format(height), # xy=(rect.get_x() + rect.get_width() / 2, height), # xytext=(0, 3), # textcoords="offset points", # ha='center', va='bottom') # autolabel(rects1) # autolabel(rects2) # autolabel(rects3) # fig.tight_layout() plt.savefig(r'C:\Users\Administrator\Desktop\p1.png',dpi=500)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
https://blog.csdn.net/luohenyj/article/details/108348697

from palettable.colorbrewer.qualitative import Pastel1_7 import matplotlib.pyplot as plt import numpy as np plt.rcParams['font.sans-serif']=['KaiTi'] plt.rcParams['axes.unicode_minus']=False fig, ax = plt.subplots(figsize=(6, 3), subplot_kw=dict(aspect="equal")) recipe = ["标签1", "标签2", "标签3", "标签4", "标签5", "标签6"] data = [225, 90, 50, 60, 100, 25] wedges, texts = ax.pie(data,colors=Pastel1_7.hex_colors,wedgeprops=dict(width=0.5), startangle=-40) # 每一类别说明框 # boxstyle框的类型,fc填充颜色,ec边框颜色,lw边框宽度 bbox_props = dict(boxstyle="square,pad=0.3", fc='white', ec="black", lw=0.72) # 设置框引出方式 kw = dict(arrowprops=dict(arrowstyle="-"), bbox=bbox_props, zorder=0, va="center") # 添加标签 for i, p in enumerate(wedges): ang = (p.theta2 - p.theta1)/2. + p.theta1 y = np.sin(np.deg2rad(ang)) x = np.cos(np.deg2rad(ang)) # 设置方向 horizontalalignment = {-1: "right", 1: "left"}[int(np.sign(x))] connectionstyle = "angle,angleA=0,angleB={}".format(ang) kw["arrowprops"].update({"connectionstyle": connectionstyle}) # 设置标注 ax.annotate(recipe[i], xy=(x, y), xytext=(1.35*np.sign(x), 1.4*y), horizontalalignment=horizontalalignment,color='black', **kw) ax.set_title("Matplotlib bakery: A donut") plt.show();
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
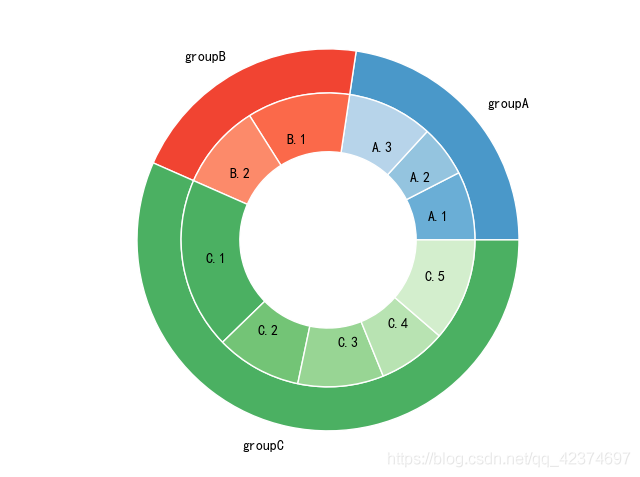
import matplotlib.pyplot as plt
group_names=['groupA', 'groupB', 'groupC']
group_size=[12,11,30]
subgroup_names=['A.1', 'A.2', 'A.3', 'B.1', 'B.2', 'C.1', 'C.2', 'C.3', 'C.4', 'C.5']
subgroup_size=[4,3,5,6,5,10,5,5,4,6]
a, b, c=[plt.cm.Blues, plt.cm.Reds, plt.cm.Greens]
fig, ax = plt.subplots()
ax.axis('equal')
mypie, _ = ax.pie(group_size, radius=1.3, labels=group_names, colors=[a(0.6), b(0.6), c(0.6)],wedgeprops=dict(width=0.3, edgecolor='white'));
mypie2, _ = ax.pie(subgroup_size, radius=1.3-0.3, labels=subgroup_names, labeldistance=0.7, colors=[a(0.5), a(0.4), a(0.3), b(0.5), b(0.4), c(0.6), c(0.5), c(0.4), c(0.3), c(0.2)],wedgeprops=dict(width=0.4, edgecolor='white'));
plt.margins(0,0);
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
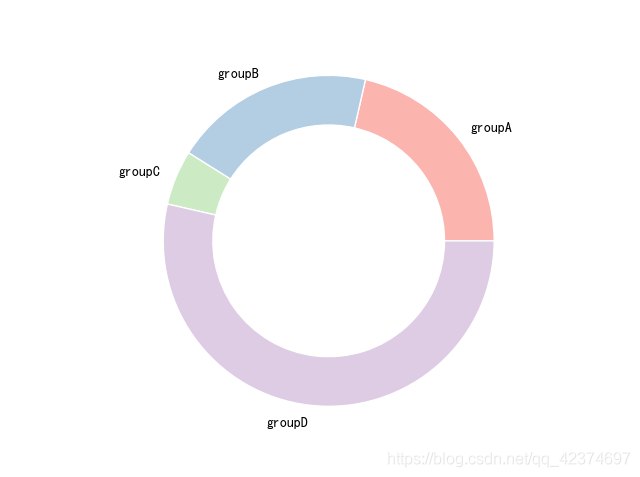
import matplotlib.pyplot as plt
names='groupA', 'groupB', 'groupC', 'groupD',
size=[12,11,3,30]
from palettable.colorbrewer.qualitative import Pastel1_7
plt.pie(size, labels=names, colors=Pastel1_7.hex_colors,wedgeprops=dict(width=0.3, edgecolor='w'))
plt.axis('equal')
plt.show();
- 1
- 2
- 3
- 4
- 5
- 6
- 7
https://zhuanlan.zhihu.com/p/140945416
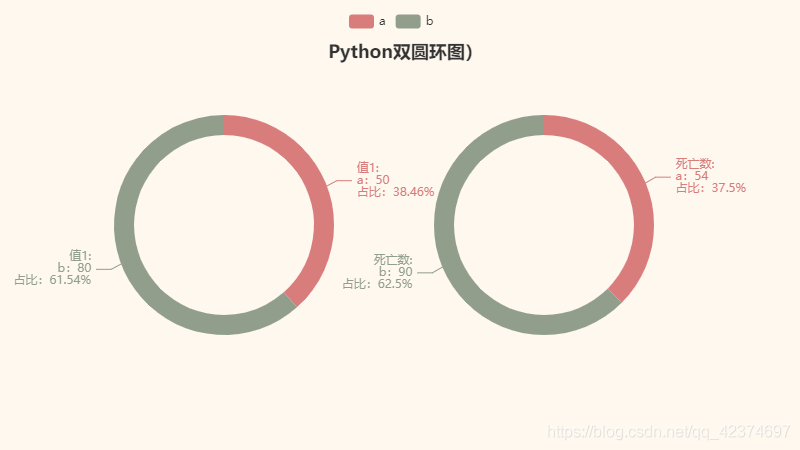
import pandas as pd from pyecharts import options as opts from pyecharts.charts import Pie from pyecharts.globals import ThemeType from pyecharts.commons.utils import JsCode b = ["a","b"] c = [50,80] d = [54,90] df_pie = pd.DataFrame({'类别':b,'值1':c,'值2':d}) fn = """ function(params) { if(params.name == '其他') return '\\n\\n\\n' + params.name + ' : ' + params.value + '%'; return params.name + ' : ' + params.value + '%'; } """ def new_label_opts(): return opts.LabelOpts(formatter=JsCode(fn), position="center") c = ( Pie(init_opts=opts.InitOpts(width="800px", height="450px",theme = ThemeType.VINTAGE )) .add( "值1", df_pie[["类别","值1"]].values.tolist(), center=["28%", "50%"], radius=[90, 110], label_opts=new_label_opts(), ) .add( "死亡数", df_pie[["类别","值2"]].values.tolist(), center=["68%", "50%"], radius=[90, 110], label_opts=new_label_opts(), ) .set_global_opts( title_opts=opts.TitleOpts(title="Python双圆环图)",pos_bottom = "85%", pos_right = "39%"), legend_opts=opts.LegendOpts( is_show=1,type_="scroll", pos_top="2%", pos_left="43%", orient="horizontal" ), toolbox_opts=opts.ToolboxOpts( # 是否显示该工具 is_show=True, ), ) .set_series_opts(label_opts = opts.LabelOpts(is_show=1,formatter="{a}:\n{b}:{c}\n占比:{d}%") ) .render("mutiple_pie.html") )
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
https://zhuanlan.zhihu.com/p/62748885
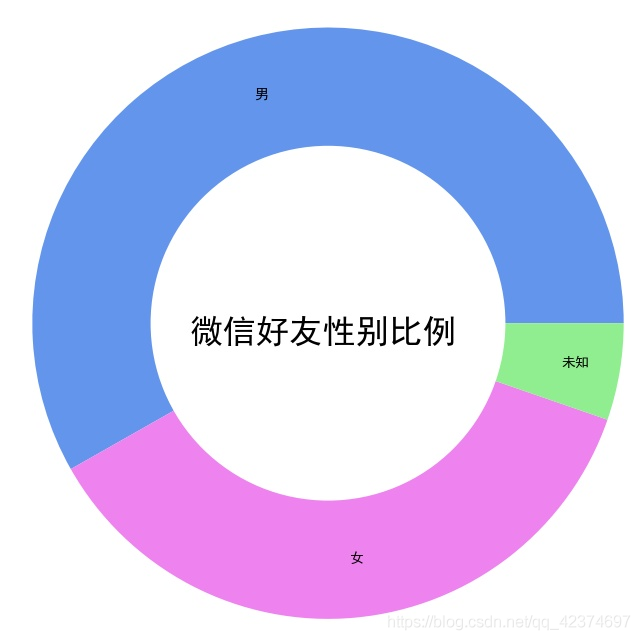
def getFrinendSex():#获取好友性别
auto_login(hotReload=True)
a=get_friends()
ls=[]
for i in a:
ls.append(i['Sex'])#性别字典键
a=['男','女','未知']
b=dict(zip(a,Counter(ls).values()))#counter统计列表中代表性别的元素(0,1,2)的个数,并替换成指定的列表a
shareN=[v/sum(b.values()) for v in b.values()]#计算各类别占比,形成列表
plt.figure(figsize=(6.4,6.4),facecolor='b')
plt.pie(x=shareN,radius=1.5,labels=a,pctdistance=1.2,labeldistance=0.8,colors=['cornflowerblue','violet','lightgreen'])
plt.pie(x=[1],radius=0.9,colors='w')#叠加一个空白的Piel图,形成环形
plt.rcParams['font.sans-serif'] = ['SimHei']#中文标签需要这个字体才能显示
plt.text(-0.7,-0.1,'微信好友性别比例',fontsize=24)#向中间空白填充此词组
plt.savefig('RawenWechatFriendSex.jpg',dpi=100)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
内嵌环形饼图
https://blog.csdn.net/bubid/article/details/108095414?utm_medium=distribute.wap_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-7.wap_blog_relevant_pic&depth_1-utm_source=distribute.wap_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-7.wap_blog_relevant_pic
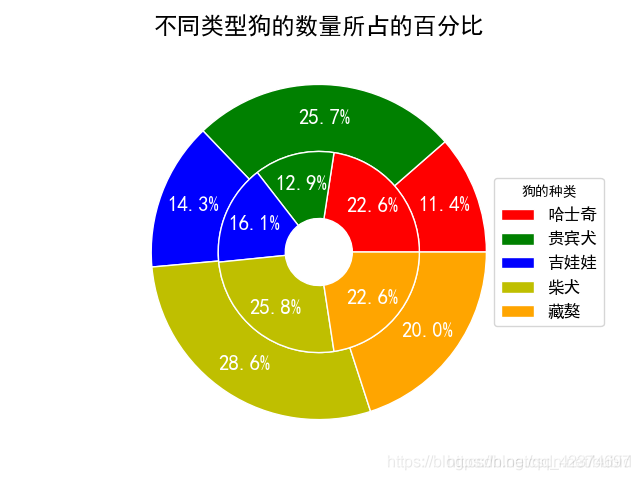
有道:1
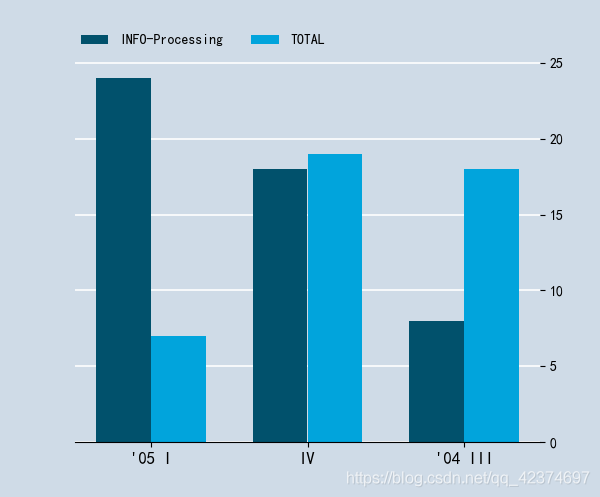
有道:2

当是一个二维表时,可以做堆叠柱形图
有道:3

#提取会员不同性别人数
male = pd.value_counts(data['GENDER'])['男']
female = pd.value_counts(data['GENDER'])['女']
#绘制会员性别比例饼图
fig = plt.figure(figsize=(7, 4)) #设置画布大小
plt.pie([male, female], labels=['男', '女'], colors=['lightskyblue', 'lightcoral'], autopct='%1.1f%%')
plt.title('会员性别比例')
plt.show()
plt.close()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
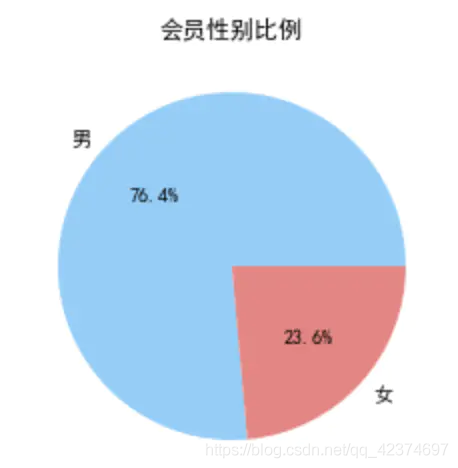
本文内容由网友自发贡献,转载请注明出处:https://www.wpsshop.cn/w/凡人多烦事01/article/detail/251228
推荐阅读
Copyright © 2003-2013 www.wpsshop.cn 版权所有,并保留所有权利。