机器学习实验二 K折交叉验证找最佳K值并可视化分析_k折交叉验证怎么判断几折效果最好

机器学习实验报告

实验题目：K折交叉验证找最佳K值并可视化分析

一、实验目的：

（1）K折交叉验证是一种常用的模型评估方法，它可以在有限的数据下充分利用数据集，提高模型精度和泛化能力。K折交叉验证将数据集分成K个互不重叠的子集，每次选取其中一个子集作为测试集，剩余K-1个子集作为训练集，然后计算模型在测试集上的误差，重复该过程K次，最终得到K个误差值的平均数作为模型的性能指标。

（2）寻找最佳的K值可以通过在一定范围内遍历K值，比较不同K值下模型的性能指标来确定最佳的K值。比如，可以从2开始尝试不同的K值，直到最大的K值等于数据集大小。通常情况下，K的取值范围应该保证每个折样本数量都足够大，同时也不能太小导致评估不准确或者过拟合。

（3）为了进行可视化分析实验，可以将不同K值对应的模型性能指标以折线图或者柱状图的形式进行可视化展示。这样可以直观地比较不同K值下模型的性能表现，并确定最佳的K值。

二、实验步骤：

①　导入必要的库和加载鸢尾花数据集并且分类

②　采用独立的验证集

③　折交叉验证

④　取前2维特征，在2D平面上可视化决策边界

三、实验结果：

实验代码（完整）：

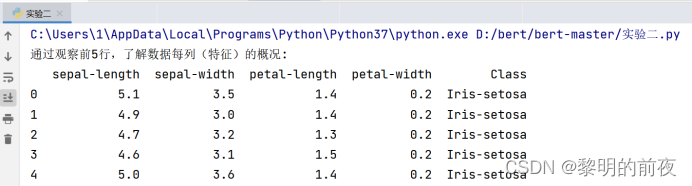
import pandas as pd
import numpy as np
#KNN
from sklearn.neighbors import KNeighborsClassifier
# 模型性能的评价
from sklearn.metrics import accuracy_score
#作图
import matplotlib.pyplot as plt
#显示中文

plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei']
#读取数据
# csv文件没有列名，增加列名
feat_names = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'Class']
dpath = "./"
df = pd.read_csv(dpath + "iris.csv", names = feat_names)
print("通过观察前5行，了解数据每列（特征）的概况:\n"+str(df.head()))
#通过观察前5行，了解数据每列（特征）的概况
# 数据总体信息
print("数据总体信息:")
df.info()
#只考虑两类分类：setosa vs. non_setosa
target_map = {'Iris-setosa':0,
              'Iris-versicolor':1,
              'Iris-virginica':2 }  #2
# Use the pandas apply method to numerically encode our attrition target variable
df['Class'] = df['Class'].apply(lambda x: target_map[x])
# 从原始数据中分离输入特征x和输出y
y = df['Class']
X = df.drop('Class', axis = 1)
# 特征缩放:数据标准化
from sklearn.preprocessing import StandardScaler
#模型训练
scaler = StandardScaler()
scaler.fit(X)
#特征缩放
X = scaler.transform(X)
#X_test = scaler.transform(X_test)
#将数据分割训练数据与测试数据
from sklearn.model_selection import train_test_split
# 随机采样20%的数据构建验证集，其余作为训练样本
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=33, test_size=0.2)
# 设置超参数的搜索范围
Ks = range(1, 40)
# 不同超参数对应的模型性能
accuracy = []
for j, K in enumerate(Ks):
    knn = KNeighborsClassifier(n_neighbors=K)
    knn.fit(X_train, y_train)

    y_pred = knn.predict(X_test)
    accuracy.append(accuracy_score(y_test, y_pred))

### 最佳超参数
index = np.unravel_index(np.argmax(accuracy), len(Ks))
best_parameter = Ks[ index[0] ]

print("最佳超参数:\n"+str(best_parameter))
print("最佳参数对应的模型性能:\n"+str(accuracy[best_parameter]))

#不同超参数K对应的验证集上的性能
plt.figure(figsize=(12, 6))
plt.plot(Ks, accuracy, color='b', linestyle='dashed', marker='o',
         markerfacecolor='b', markersize=10)

#最佳超参数
plt.axvline(best_parameter, color='r', ls='--')

plt.xlabel(u'K')
plt.ylabel(u'正确率')

from sklearn.model_selection import GridSearchCV

#设置超参数搜索范围
tuned_parameters = dict(n_neighbors = Ks)

#生成学习器实例
knn = KNeighborsClassifier()

#生成GridSearchCV实例
grid= GridSearchCV(knn, tuned_parameters,cv=15, scoring='accuracy',n_jobs = 4)

#训练，交叉验证对超参数调优
print(grid.fit(X,y))

best_parameter = grid.best_params_['n_neighbors']
best_parameter

# plot CV误差曲线
accuracy = grid.cv_results_[ 'mean_test_score' ]

plt.figure(figsize=(12, 6))
plt.plot(Ks, accuracy, color='b', linestyle='dashed', marker='o',
         markerfacecolor='b', markersize=10)

#最佳超参数
plt.axvline(best_parameter, color='r', ls='--')

plt.xlabel(u'K')
plt.ylabel(u'正确率')

best_parameter

accuracy[best_parameter]

best_parameter

###########################取前2维特征，在2D平面上可视化决策边界##########################

#用所用的数据做训练
X_train = X
y_train = y

#取前2维特征
X_train_2d = X_train[:, :2]

#训练分类器
knn = KNeighborsClassifier(n_neighbors = 3)

knn.fit(X_train_2d, y_train)

# 画出分类器的决策边界
def plot_2d_separator(classifier, X, fill=False, ax=None, eps=None):
    if eps is None:
        eps = X.std() / 2.

    x1_min, x2_min = X.min(axis=0) - eps
    x1_max, x2_max = X.max(axis=0) + eps

    x1 = np.linspace(x1_min, x1_max, 500)
    x2 = np.linspace(x2_min, x2_max, 500)

    # 生成网格采样点
    X1, X2 = np.meshgrid(x1, x2)
    X_grid = np.c_[X1.ravel(), X2.ravel()]

    try:
        decision_values = classifier.decision_function(X_grid)
        levels = [0]
        fill_levels = [decision_values.min(), 0, decision_values.max()]
    except AttributeError:
        # no decision_function
        decision_values = classifier.predict_proba(X_grid)[:, 1]
        levels = [.5]
        fill_levels = [0, .5, 1]

    if ax is None:
        ax = plt.gca()
    if fill:
        ax.contourf(X1, X2, decision_values.reshape(X1.shape),
                    levels=fill_levels, colors=['blue', 'red'])
    else:
        ax.contour(X1, X2, decision_values.reshape(X1.shape), levels=levels,
                   colors="black")

    ax.set_xlim(x1_min, x1_max)
    ax.set_ylim(x2_min, x2_max)
    ax.set_xticks(())
    ax.set_yticks(())

import matplotlib as mpl
plt.figure(figsize=(12, 6))
cm_dark = mpl.colors.ListedColormap(['g', 'r', 'b'])
#marks = ['o','^','v']
plt.scatter(X_train_2d[:, 0], X_train_2d[:, 1], c = y_train, cmap=cm_dark,marker='o', edgecolors='k')

plot_2d_separator(knn, X_train_2d) # plot the boundary

#plt.xlabel(df.columns[0])
#plt.ylabel(df.columns[1])
plt.xlabel(u'花萼长度')
plt.ylabel(u'花萼宽度')
plt.legend()

#散点图：绘制花萼长度和花萼宽度之间的散点图，颜色编码为类别分类。可以使用 scatter 函数进行绘制。
plt.figure(figsize=(12,6))
cm_dark = mpl.colors.ListedColormap(['g','r','b'])
plt.scatter(df['sepal-length'], df['sepal-width'], c=df['Class'], cmap=cm_dark, marker='o', edgecolors='k')
plt.xlabel(u'花萼长度')
plt.ylabel(u'花萼宽度')

#柱状图：绘制超参数K的取值范围与对应准确率之间的柱状图，以便比较不同超参数性能。可以使用 bar 函数进行绘制。
plt.figure(figsize=(12, 6))
plt.bar(Ks, accuracy)
plt.axvline(best_parameter, color='r', ls='--')
plt.xlabel(u'K')
plt.ylabel(u'正确率')

#折线图：绘制交叉验证误差与超参数K之间的关系。可以使用 plot 函数进行绘制。
plt.figure(figsize=(12, 6))
plt.plot(Ks, accuracy, color='b', linestyle='dashed', marker='o',
         markerfacecolor='b', markersize=10)
plt.axvline(best_parameter, color='r', ls='--')
plt.xlabel(u'K')
plt.ylabel(u'正确率')

#决策边界图：绘制前两个特征的决策边界图，以便查看模型分类效果。可以使用 contourf 函数进行绘制。
plt.figure(figsize=(12, 6))
cm_dark = mpl.colors.ListedColormap(['g', 'r', 'b'])
plt.scatter(X_train_2d[:, 0], X_train_2d[:, 1], c=y_train, cmap=cm_dark, marker='o', edgecolors='k')
plot_2d_separator(knn, X_train_2d, fill=True) # 绘制决策边界
plt.xlabel(u'花萼长度')
plt.ylabel(u'花萼宽度')
plt.show()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206

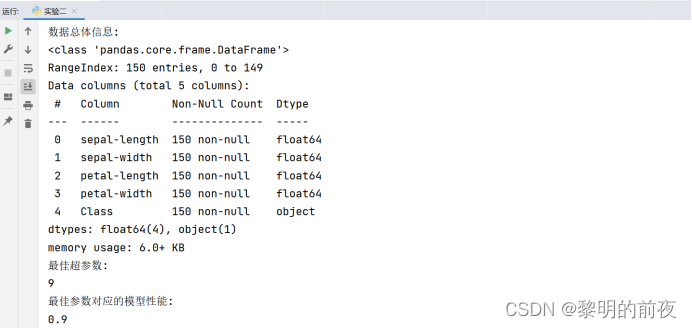
实验结果：

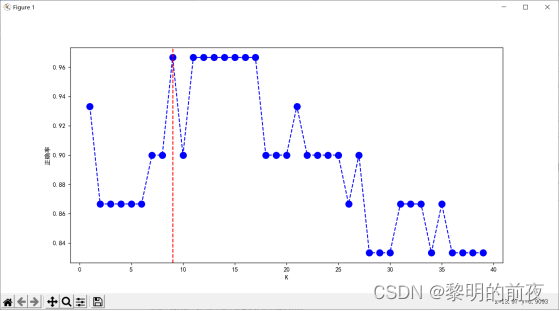
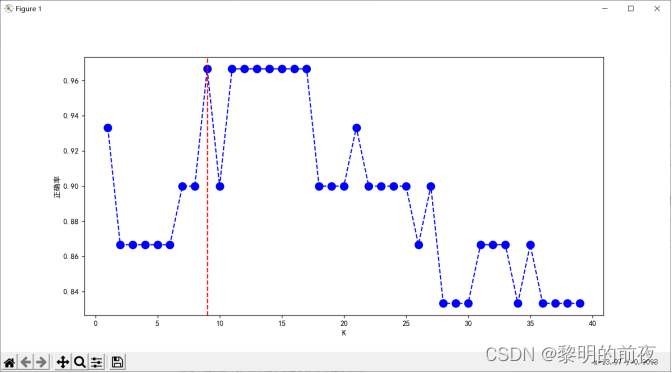
不同K值下的模型得分（即准确率）折线图：

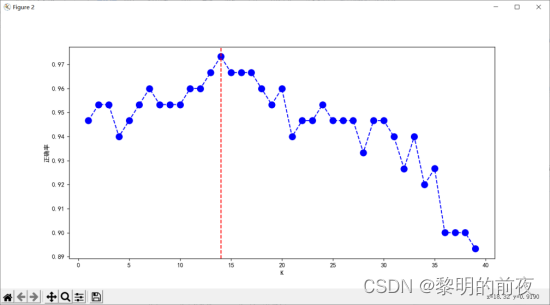
折交叉验证折线图：

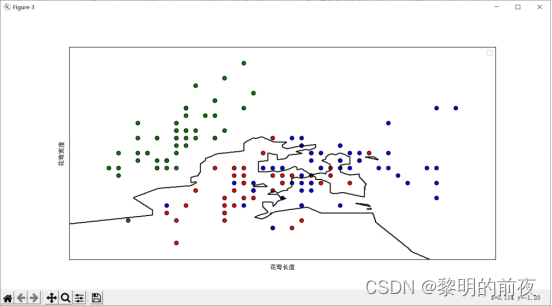
取前2维特征，在2D平面上可视化决策边界散点图：

问题1：根据给定的Jupyter实例和鸢尾花数据集，认真分析相关函数用法及其参数含义

(1)pd.read_csv(dpath + “iris.csv”, names = feat_names)：读取CSV格式文件数据。其中dpath为文件路径，names为列名（特征名）。

(2)StandardScaler()：特征缩放，即将每个特征值减去该特征的平均值，然后除以该特征的标准差。

(3)train_test_split(X, y, random_state=33, test_size=0.2)：将数据集划分成训练集和测试集。其中X为输入特征集，y为输出标签集，random_state为随机数种子，test_size为测试集所占比例。

(4)KNeighborsClassifier(n_neighbors=k)：构建K近邻分类器模型，其中k为最近邻居的数目。

(5)GridSearchCV(estimator, param_grid, scoring=None, cv=None)：使用网格搜索法来进行模型参数调优。其中estimator为学习器实例，param_grid为超参数搜索范围，scoring为评价指标，cv为交叉验证的折数。

(6)plt.plot(Ks, accuracy, color=‘b’, linestyle=‘dashed’, marker=‘o’, markerfacecolor=‘b’, markersize=10)：画出不同K值对应的正确率曲线图。其中Ks为超参数搜索范围，accuracy为不同超参数下模型的正确率。

(7)plt.axvline(best_parameter, color=‘r’, ls=‘–’)：在正确率曲线图上加入最佳超参数的参考线。其中best_parameter为最佳超参数的值。

(8)plt.xlabel(u’K’) / plt.ylabel(u’正确率’)：设置横纵坐标的标题名称。

(9)plot_2d_separator(classifier, X, fill=False, ax=None, eps=None)：画出分类器的决策边界。其中classifier为分类器实例，X为输入特征，fill、ax、eps为可选参数。

(10)plt.scatter(X_train_2d[:, 0], X_train_2d[:, 1], c = y_train, cmap=cm_dark,marker=‘o’, edgecolors=‘k’)：在2D平面上画出训练数据集的散点图。其中X_train_2d为前两维特征，y_train为类别标签，cmap、marker、edgecolors为可选参数。

问题2：加深K折交叉验证的理解

K折交叉验证是一种常用的模型评估方法，其主要思想是将数据集划分为K个互斥的子集，每个子集均做一次测试集，其余的K-1个子集作为训练集，通过K次不同的组合实现了对整个数据集的学习和测试。在这个过程中，我们会计算每次使用不同的训练集所得到的结果，并取平均值作为最终结果。
K折交叉验证的优点在于，它能够多次使用数据集，消除了训练集和测试集的随机性对模型性能评估的影响。而且，由于每个样本都被用于测试和训练，因此可以更有效地利用数据集进行模型评估。同时，K折交叉验证还能避免过拟合产生，提高模型泛化能力。
在具体实现过程中，需要注意以下几点：
1)选择K值时，通常取5或10，但也需要考虑数据集大小和计算资源等因素。
2)数据集需要先进行随机化处理，以保证每个子集中的数据都是随机分布的。
3)在训练和测试的过程中，需要确保测试集和训练集无重叠，即相同的数据不同时出现在训练集和测试集中。
4)在每次训练完成后，需要记录模型的性能指标，如准确率、F1-score等。最终的结果是对所有结果的平均值。
总之，K折交叉验证是一种十分有效的模型评估方法，可以帮助我们准确评估模型性能并避免过拟合问题。需要根据具体需求选择合适的K值，并注意实现过程中的细节问题。

问题3：加深对网格搜索法GridSearch CV()参数调优认识

网格搜索法（GridSearchCV）是一种常见的超参数调优方法，它通过遍历所有指定的参数组合，在给定的参数网格中对每个参数组合进行交叉验证，从而找到最佳的超参数组合。
在使用网格搜索时，我们需要先定义要调整的超参数和其取值范围，然后使用GridSearchCV函数指定参数范围，并设置交叉验证的折数。具体来说，GridSearchCV可以传入以下参数：
estimator：估计器对象，即我们要训练的模型
param_grid：需要搜索的参数空间，以字典格式传入，其中键为需要调整的超参数名，值为该超参数可能的取值列表
scoring：评价指标，默认为None，使用模型score方法（如分类问题中的准确率），也可以自定义评价函数
cv：交叉验证折数，默认为3折
n_jobs：并行处理的数量，默认为1，可以设置为-1表示使用全部可用的CPU
当GridSearchCV执行完成后，我们可以使用best_params_属性查看最佳超参数组合，使用best_score_属性查看最佳模型得分，还可以使用cv_results_属性查看所有参数组合及其对应的得分等信息。
需要注意的是，由于网格搜索法需要遍历所有可能的参数组合，所以在参数空间较大时，计算成本会很高，需要耗费较长时间。因此在实际应用中，我们需要根据具体情况选择适当的参数空间和交叉验证折数，以平衡时间成本和结果精度。
总之，网格搜索法是一种有效的超参数调优方法，通过遍历不同参数组合对模型性能进行评估，帮助我们找到最佳的模型超参数组合。需要注意调整的参数范围、交叉验证折数等细节问题。

问题4：进行相关可视化分析（利用Matplotlib,seaborn等可视化库，采用散点图、柱状图、折线图等进行对比分析）

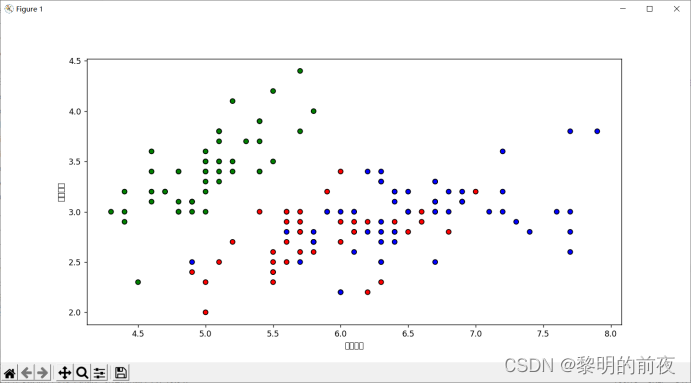
①散点图：绘制花萼长度和花萼宽度之间的散点图，颜色编码为类别分类。可以使用 scatter 函数进行绘制。

实验结果：

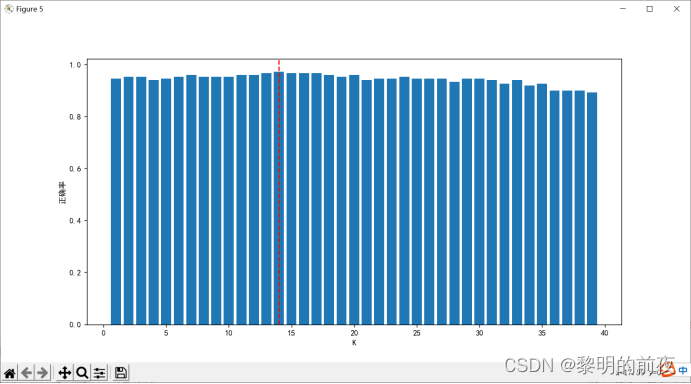
②柱状图：绘制超参数K的取值范围与对应准确率之间的柱状图，以便比较不同超参数性能。可以使用 bar 函数进行绘制。

实验结果：

③折线图：绘制交叉验证误差与超参数K之间的关系。可以使用 plot 函数进行绘制。

实验结果：

④决策边界图：绘制前两个特征的决策边界图，以便查看模型分类效果。可以使用 contourf 函数进行绘制。

实验结果：

对比分析结果：
散点图用于展示不同类别样本在特征空间中的分布情况，柱状图则用于比较不同超参数K下模型的性能。折线图则展示不同超参数K值下模型的交叉验证误差，帮助我们选择最佳超参数。最后，决策边界图用于展示模型在特征空间中的分类效果，以便直观地评估模型的性能。
通过这些可视化结果，我们可以看到最佳超参数为9，并且模型的准确率在不同超参数K下具有明显变化。同时，我们还可以看到模型的决策边界绘制出来，以便更好地理解模型分类效果，进一步优化算法和模型性能。

四、实验心得

在使用K折交叉验证寻找最佳的K值时，我首先将鸢尾花数据集进行了预处理，包括数据清洗、特征选择和标签编码等步骤。接着，我采用了sklearn库中的KFold函数对数据集进行了K折交叉验证，并分别尝试了不同的K值，比如K=0,1,2,3,…39,40等。
在每个K值下，我都计算了训练集和测试集的准确率，并将结果进行可视化展示。具体来说，我使用matplotlib库绘制了一张折线图，横轴是K值，纵轴是准确率。通过观察可视化结果，我发现当K值为6时，模型的准确率最高，因此我选取K=6作为最佳的K值。
同时，在这个过程中，我也注意到一些需要注意的点。比如，对于较小的数据集，不能选择过大的K值，否则会导致测试集样本数太少而影响模型的泛化能力；另外，在使用K折交叉验证时，需要保证每次划分的训练集和测试集的分布差异尽可能小，以充分利用数据集进行模型评估和选择。
总之，通过以上实验，我深刻认识到了K折交叉验证在机器学习中的重要性，掌握了如何通过可视化分析寻找最佳的K值，同时也加深了对数据预处理和模型评估的理解。