凡人多烦事01

这个屌丝很懒，什么也没留下！

热门标签

Python解答蓝桥杯省赛真题之从入门到真题_蓝桥杯python题库及答案

作者：凡人多烦事01 | 2024-04-13 12:10:35

踩

蓝桥杯python题库及答案

在这里插入图片描述

想看更多算法题，可以扫描上方二维码关注我微信公众号“数据结构和算法”，截止到目前我已经在公众号中更新了500多道算法题，其中部分已经整理成了pdf文档，截止到目前总共有900多页（并且还会不断的增加），可以在公众号中回复关键字“pdf”即可下载。

本文转载自：Python解答蓝桥杯省赛真题之从入门到真题

文章目录

1.入门篇
2.基础篇
3.提高篇
4.真题篇

1.入门篇

1.1 Fibonacci数列题

问题描述

Fibonacci数列的递推公式为：Fn=Fn-1+Fn-2，其中F1=F2=1。
当n比较大时，Fn也非常大，现在我们想知道，Fn除以10007的余数是多少。

输入描述
n
输入格式输入包含一个整数n。

输出描述

输出格式输出一行，包含一个整数，表示Fn除以10007的余数。

说明：在本题中，答案是要求Fn除以10007的余数，因此我们只要能算出这个余数即可，而不需要先计算出Fn的准确值，再将计算的结果除以10007取余数，直接计算余数往往比先算出原数再取余简单。
数据规模与约定1 <= n <= 1,000,000

n = int(input())

Fib = [1 for i in range(n+1)]

k = 3

while k<=n:
    
    Fib[k] = (Fib[k-1] + Fib[k-2]) % 10007

    k += 1

print(Fib[n])
1
2
3
4
5
6
7
8
9
10
11
12
13

1.2 入门训练圆的面积

问题描述

给定圆的半径r，求圆的面积。

输入格式

输入包含一个整数r，表示圆的半径。

输出格式

输出一行，包含一个实数，四舍五入保留小数点后7位，表示圆的面积。

样例输入

样例输出

50.2654825

数据规模与约定

1 <= r <= 10000。

import math

r = int(input())

area = math.pi * r * r

print('%.7f' % area)
1
2
3
4
5
6
7

1.3 入门训练序列求和

问题描述

求1+2+3+…+n的值。

输入格式

输入包括一个整数n。

输出格式

输出一行，包括一个整数，表示1+2+3+…+n的值。

样例输入

样例输出

数据规模与约定

1 <= n <= 1,000,000,000.

注意不要用循环来做，否则当数据规模变大时会超时

n = int(input())

s = n * (n + 1) / 2 # 等差数列公式，节省很多时间

print('%d' % s)
1
2
3
4
5

1.4 入门训练 A+B问题

问题描述

输入A、B，输出A+B。

输入格式

输入的第一行包括两个整数，由空格分隔，分别表示A、B。

输出格式

输出一行，包括一个整数，表示A+B的值。

样例输入

12 45

样例输出

数据规模与约定

-10000 <= A, B <= 10000

# 注意：本体数据规模较小，可以正常计算
# 若数据规模过大，则考虑用字符串存取大数，然后用大数加法来计算结果并输出
a, b = map(int, input().split())
print(a + b)
1
2
3
4

2.基础篇

2.1 数列排序

问题描述
　　给定一个长度为n的数列，将这个数列按从小到大的顺序排列。1<=n<=200
输入格式
　　第一行为一个整数n。
　　第二行包含n个整数，为待排序的数，每个整数的绝对值小于10000。
输出格式
　　输出一行，按从小到大的顺序输出排序后的数列。
样例输入
5
8 3 6 4 9
样例输出
3 4 6 8 9

# 代码1
n = int(input())
arr = list(map(int, input().split()))
arr.sort()
for i in range(n):
    print(arr[i], end=' ')
   
1
2
3
4
5
6
7

# 代码2
n = int(input())
arr = list(map(int, input().split()))
arr.sort()
for i in range(n - 1):
    print(arr[i], end=' ')
print(arr[n-1])
1
2
3
4
5
6
7

# 代码3
n = int(input())
arr = list(map(int, input().split()))
arr.sort()
for i in range(n - 1):
    print(arr[i], end=' ')
print(arr[n-1], end='')
1
2
3
4
5
6
7

蓝桥的练习系统没有OJ那么严格，故意试了一下，代码1最后一个数字输出时后边会有一个空格，OJ上这样是不予通过的，但是蓝桥练习系统这样提交了之后仍然通过。代码2最后无空格进行换行，蓝桥练习系统也通过了。代码3最后不换行，也不输出空格，输出最后一个数后就停止，蓝桥练习系统也通过了。看来对这个蓝桥要求不严格。考试时自己斟酌。

2.2 十六进制转八进制

问题描述
　　给定n个十六进制正整数，输出它们对应的八进制数。

输入格式
　　输入的第一行为一个正整数n （1<=n<=10）。
　　接下来n行，每行一个由0_{9、大写字母A}F组成的字符串，表示要转换的十六进制正整数，每个十六进制数长度不超过100000。

输出格式
　　输出n行，每行为输入对应的八进制正整数。

【注意】
　　输入的十六进制数不会有前导0，比如012A。
　　输出的八进制数也不能有前导0。

样例输入
　　2
　　39
　　123ABC

样例输出
　　71
　　4435274

【提示】
　　先将十六进制数转换成某进制数，再由某进制数转换成八进制。

t = int(input())
# print(t)
for i in range(t):
    n = input()
    # ans = oct(int(n, 16))
    # print(ans[2:])
    ans = format(int(n, 16), 'o')
    print(ans)


1
2
3
4
5
6
7
8
9
10

参考知识

Python的进制转换函数
 Python的int()函数
 python 如何实现对字符和ASCII码的转换

2.3 十六进制转十进制

问题描述
　　从键盘输入一个不超过8位的正的十六进制数字符串，将它转换为正的十进制数后输出。
　　注：十六进制数中的10~15分别用大写的英文字母A、B、C、D、E、F表示。
样例输入
FFFF
样例输出
65535

n = input()
print(int(n, 16))
# 你没有看错，python就是这么干脆，两行搞定
1
2
3

2.4 十进制转十六进制

问题描述
　　十六进制数是在程序设计时经常要使用到的一种整数的表示方式。它有0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F共16个符号，分别表示十进制数的0至15。十六进制的计数方法是满16进1，所以十进制数16在十六进制中是10，而十进制的17在十六进制中是11，以此类推，十进制的30在十六进制中是1E。
　　给出一个非负整数，将它表示成十六进制的形式。
输入格式
　　输入包含一个非负整数a，表示要转换的数。0<=a<=2147483647
输出格式
　　输出这个整数的16进制表示
样例输入
30
样例输出
1E

n = int(input())
print(format(n, 'X')) # x 输出字母为小写 X 输出字母为大写
1
2

2.5 特殊回文数

问题描述
　　123321是一个非常特殊的数，它从左边读和从右边读是一样的。
　　输入一个正整数n，编程求所有这样的五位和六位十进制数，满足各位数字之和等于n 。
输入格式
　　输入一行，包含一个正整数n。
输出格式
　　按从小到大的顺序输出满足条件的整数，每个整数占一行。
样例输入
52
样例输出
899998
989989
998899
数据规模和约定
　　1<=n<=54。

Python这个时候我发现出了点问题：
同样的代码C写的程序会比Python写的程序运行时间短。
上述题目时限为1s，C程序如下，蓝桥练习系统提交通过。

#include<stdio.h>
int a(int n)//求出5位数和6位数中的回文数函数 
{
	int i,j,sum,temp,len;
	int a,b,c;
	for(i=10000;i<1000000;++i)
	{
		sum=0;
		temp=i;
		len=0;
		while(temp!=0)
		{
			sum=sum*10+temp%10;
			temp=temp/10;
			len++;//累计位数以此判断是5位数还是6位数 
		}
		if(sum==i)//先把回文数求出来，下面再来比较各位数字之和是否等于n 
		{
			a=i%10;//个位 
			b=i/10%10;//十位
			c=i/100%10;//百位 
			
			if(5==len)
			{
				if(n==(2*a+2*b+c))
				{
					printf("%d\n",i);
				 } 
			}
			if(6==len)
			{
				if(n==(2*a+2*b+2*c))
				{
					printf("%d\n",i); 
				}
			}
		}
	}
}
//主函数 
int main()
{
	int n;
	scanf("%d",&n);
	a(n);
	return 0;
 } 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

然而把语言换成Python，算法思想一样，提交却超时，一看，时间已经为5s多了

#include<stdio.h>
int a(int n)//求出5位数和6位数中的回文数函数 
{
	int i,j,sum,temp,len;
	int a,b,c;
	for(i=10000;i<1000000;++i)
	{
		sum=0;
		temp=i;
		len=0;
		while(temp!=0)
		{
			sum=sum*10+temp%10;
			temp=temp/10;
			len++;//累计位数以此判断是5位数还是6位数 
		}
		if(sum==i)//先把回文数求出来，下面再来比较各位数字之和是否等于n 
		{
			a=i%10;//个位 
			b=i/10%10;//十位
			c=i/100%10;//百位 
			
			if(5==len)
			{
				if(n==(2*a+2*b+c))
				{
					printf("%d\n",i);
				 } 
			}
			if(6==len)
			{
				if(n==(2*a+2*b+2*c))
				{
					printf("%d\n",i); 
				}
			}
		}
	}
}
//主函数 
int main()
{
	int n;
	scanf("%d",&n);
	a(n);
	return 0;
 } 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

运行结果
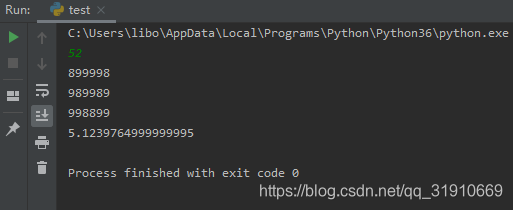
在这里插入图片描述
时间为5.1s多
自己又写了一个代码

import time

start = time.clock()

def is_pal(i_):
    i_s = str(i_)
    if i_s == i_s[::-1]:
        return True
    else:
        return False


def sum_i(i_):
    s = 0
    i_s = str(i)
    for j in range(len(i_s)):
        s += int(i_s[j])
    return s


n = int(input())
i = 10000
while i < 1000000:
    if is_pal(i):
        if sum_i(i) == n:
            print(i)
    i += 1

end = time.clock()

print(end - start)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

运行结果
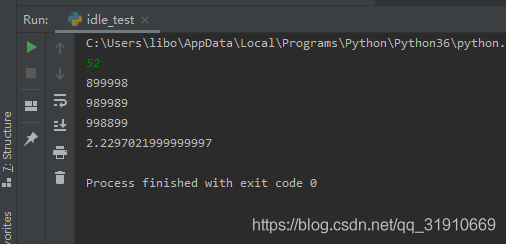
在这里插入图片描述
时间为2s多，还是不通过。
目前不清楚这个问题要怎么解决，待解答。

2.6 回文数

正着数和倒着数都一样，输出所有的这样的四位数
如 1221

def is_pal(i_):
    i_s = str(i_)
    if i_s == i_s[::-1]:
        return True
    else:
        return False


i = 1000
while i < 10000:
    if is_pal(i):
        print(i)
    i += 1
1
2
3
4
5
6
7
8
9
10
11
12
13

2.7 水仙花数

问题描述
　　153是一个非常特殊的数，它等于它的每位数字的立方和，即153=111+555+333。编程求所有满足这种条件的三位十进制数。
输出格式
　　按从小到大的顺序输出满足条件的三位十进制数，每个数占一行。

def is_nar(i_):
    a = i_ % 10 # 十位
    b = int((i_ / 10)) % 10 # 百位 注意Python中除法一定会得到浮点数 要取整 而C中则不需要
    c = int(i_ / 100)
    if i_ == a ** 3 + b ** 3 + c ** 3:
        return True
    else:
        return False


i = 100
while i < 1000:
    if is_nar(i):
        print(i)
    i += 1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

2.8 杨辉三角

问题描述

杨辉三角形又称Pascal三角形，它的第i+1行是(a+b)ⁱ的展开式的系数。

它的一个重要性质是：三角形中的每个数字等于它两肩上的数字相加。

下面给出了杨辉三角形的前4行：

1 1

1 2 1

1 3 3 1

给出n，输出它的前n行。
输入格式

输入包含一个数n。
输出格式
输出杨辉三角形的前n行。每一行从这一行的第一个数开始依次输出，中间使用一个空格分隔。请不要在前面输出多余的空格。
样例输入
4
样例输出
1
1 1
1 2 1
1 3 3 1
数据规模与约定
1 <= n <= 34。

n = int(input())

k = 2

triangle_yang = [] # 杨辉三角

for i in range(n): # 定义空的杨辉三角
    triangle_yang.append([0 for j in range(i+1)])

# print(triangle_yang)
# exit()
for i in range(n): # 第一列和每一行的最后一个为1
    triangle_yang[i][0] = triangle_yang[i][-1] = 1

while k < n:
    m = 1
    while m < k: # 两肩数值之和
        triangle_yang[k][m] = triangle_yang[k-1][m-1] + triangle_yang[k-1][m]
        m += 1
    k += 1

for i in range(n): # 输出杨辉三角
    for j in range(i+1):
        print(triangle_yang[i][j], end=' ')
    print()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

2.9 查找整数

问题描述

给出一个包含n个整数的数列，问整数a在数列中的第一次出现是第几个。
输入格式

第一行包含一个整数n。

第二行包含n个非负整数，为给定的数列，数列中的每个数都不大于10000。

第三行包含一个整数a，为待查找的数。
输出格式
如果a在数列中出现了，输出它第一次出现的位置(位置从1开始编号)，否则输出-1。
样例输入
6
1 9 4 8 3 9
9
样例输出
2
数据规模与约定
1 <= n <= 1000。

n = int(input())

arr = input().split()

a = input()

i = 0

while i < n:
    if a == arr[i]:
        print(i+1)
        break
    i += 1

if i == n:
    print(-1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

2.10 数列特征

问题描述

给出n个数，找出这n个数的最大值，最小值，和。
输入格式

第一行为整数n，表示数的个数。

第二行有n个数，为给定的n个数，每个数的绝对值都小于10000。
输出格式
输出三行，每行一个整数。第一行表示这些数中的最大值，第二行表示这些数中的最小值，第三行表示这些数的和。
样例输入
5
1 3 -2 4 5
样例输出
5
-2
11
数据规模与约定
1 <= n <= 10000。

n = int(input())

arr = input().split()

print(max(int(arr[i]) for i in range(n))) # 最大值
print(min(int(arr[i]) for i in range(n))) # 最小值
print(sum(int(arr[i]) for i in range(n))) # 求和
1
2
3
4
5
6
7

注意

python的列表中的sort()函数是无法对有负数元素的列表进行排序的，这点需要谨记，以防后续使用中出现错误

2.11 字母图形

问题描述

利用字母可以组成一些美丽的图形，下面给出了一个例子：

ABCDEFG

BABCDEF

CBABCDE

DCBABCD

EDCBABC

这是一个5行7列的图形，请找出这个图形的规律，并输出一个n行m列的图形。
输入格式
输入一行，包含两个整数n和m，分别表示你要输出的图形的行数的列数。
输出格式
输出n行，每个m个字符，为你的图形。
样例输入
5 7
样例输出
ABCDEFG
BABCDEF
CBABCDE
DCBABCD
EDCBABC
数据规模与约定
1 <= n, m <= 26。

n, m = map(int, input().split())

graph = [[0 for j in range(m)] for i in range(n)] # 空二维数组

for i in range(n):
    for j in range(m):
        if j >= i: # 数组中字母规律
            graph[i][j] = chr(ord('A') + j - i)
        else:
            graph[i][j] = chr(ord('A') + i - j)

for i in range(n): # 输出二维数组
    for j in range(m):
        print(graph[i][j], end='')
    print()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

字符转ASCII码函数：ord(‘A’)–>64
ASCII码转字符函数：chr(64)–>A
以上进制转换题目提到过ASCII码与字符转换，可以点击链接观看。

2.12 字串01

问题描述

对于长度为5位的一个01串，每一位都可能是0或1，一共有32种可能。它们的前几个是：

00000

00001

00010

00011

00100

请按从小到大的顺序输出这32种01串。
输入格式
本试题没有输入。
输出格式
输出32行，按从小到大的顺序每行一个长度为5的01串。
样例输出
00000
00001
00010
00011
<以下部分省略>

# Python就是两行解决问题。。。
for i in range(32):
    print("{0:0>5}".format(format(i, 'b')))
1
2
3

参考资料

str.format添加前导零
 Format Specification Mini-Language
Python的另外三种补0方法（其实就是字符串处理函数）这里不再做代码演示，请读者自行尝试。

2.13 闰年判断

问题描述

给定一个年份，判断这一年是不是闰年。

当以下情况之一满足时，这一年是闰年：

年份是4的倍数而不是100的倍数；
年份是400的倍数。

其他的年份都不是闰年。
输入格式
输入包含一个整数y，表示当前的年份。
输出格式
输出一行，如果给定的年份是闰年，则输出yes，否则输出no。

说明：当试题指定你输出一个字符串作为结果（比如本题的yes或者no，你需要严格按照试题中给定的大小写，写错大小写将不得分。
样例输入
2013
样例输出
no
样例输入
2016
样例输出
yes
数据规模与约定
1990 <= y <= 2050。

def is_leap_year(year):
    if year % 4 == 0 and year % 100 != 0 or year % 400 == 0:
        return True
    return False


year = int(input())

if is_leap_year(year):
    print('yes')
else:
    print('no')
1
2
3
4
5
6
7
8
9
10
11
12

装逼解法

# 装逼解法
import datetime  # python的标准库，蓝桥考试可以放心使用

year = int(input())
# class datetime.timedelta(days=0, seconds=0, microseconds=0, milliseconds=0, minutes=0, hours=0, weeks=0)
# All arguments are optional and default to 0. Arguments may be integers or floats, and may be positive or negative.
time_delta = datetime.timedelta(days=1)  # 存储时间的变化量
# class datetime.date(year, month, day)
dt = datetime.date(year=year, month=3, day=1)  # 指定输入年份的3月1号

res = dt - time_delta  # 让dt存储的日期往前走一天
# print(dt)

if res.day == 29:  # 如果那年的2月分又29天为闰年
    print('yes')
else:
    print('no')
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

2.14 阶乘计算

问题描述
　　输入一个正整数n，输出n!的值。
　　其中n!=123*…*n。
算法描述
　　n!可能很大，而计算机能表示的整数范围有限，需要使用高精度计算的方法。使用一个数组A来表示一个大整数a，A[0]表示a的个位，A[1]表示a的十位，依次类推。
　　将a乘以一个整数k变为将数组A的每一个元素都乘以k，请注意处理相应的进位。
　　首先将a设为1，然后乘2，乘3，当乘到n时，即得到了n!的值。
输入格式
　　输入包含一个正整数n，n<=1000。
输出格式
　　输出n!的准确值。
样例输入
10
样例输出
3628800
特别注意n的规模
首先用递归只能解决1到几百以内的阶乘

def factorial(n):
	if n == 1:
		return n
	else:
		return n * factorial(n-1)
	
n = int(input())

result = factorial(n)

print(result)
1
2
3
4
5
6
7
8
9
10
11

这种递归方式1000的阶乘是算不了的！
去网上查询到了一个用数组处理大数阶乘的思想方法，跟题目要求的一样，用Python写了一下，提交后运行超时？！

n = int(input())
a = [0 for i in range(10000)]
a[0] = length = 1
for i in range(2, n + 1):
    carry = 0
    for j in range(length):
        temp = a[j] * i + carry
        carry = int(temp / 10)
        a[j] = temp % 10
    while carry > 0:
        a[length] += carry % 10
        length += 1
        carry = int(carry / 10)


while length > 0:
    length -= 1
    print(a[length], end='')
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

真。。。。
然后用最简单的连乘计算，发现提交过了，100分，emmmmmmm…
代码如此简单

n = int(input())

a = s =1

while a <= n:
    s = s * a
    a += 1
print(s)
1
2
3
4
5
6
7
8

看来有时候想的太多也不见得是一种好事啊！

2.15 长整数加法

问题描述
　　输入两个整数a和b，输出这两个整数的和。a和b都不超过100位。
算法描述
　　由于a和b都比较大，所以不能直接使用语言中的标准数据类型来存储。对于这种问题，一般使用数组来处理。
　　定义一个数组A，A[0]用于存储a的个位，A[1]用于存储a的十位，依此类推。同样可以用一个数组B来存储b。
　　计算c = a + b的时候，首先将A[0]与B[0]相加，如果有进位产生，则把进位（即和的十位数）存入r，把和的个位数存入C[0]，即C[0]等于(A[0]+B[0])%10。然后计算A[1]与B[1]相加，这时还应将低位进上来的值r也加起来，即C[1]应该是A[1]、B[1]和r三个数的和．如果又有进位产生，则仍可将新的进位存入到r中，和的个位存到C[1]中。依此类推，即可求出C的所有位。
　　最后将C输出即可。
输入格式
　　输入包括两行，第一行为一个非负整数a，第二行为一个非负整数b。两个整数都不超过100位，两数的最高位都不是0。
输出格式
　　输出一行，表示a + b的值。
样例输入
20100122201001221234567890
2010012220100122
样例输出
20100122203011233454668012

def change_length(arr, l):
	"""此方法使两字符串长度相等"""
    arr = '0' * (l - len(arr)) + arr
    return arr


arr = input()
arr_2 = input()

# 两数长度若不等，短的数加前导0
if len(arr) > len(arr_2):
    arr_2 = change_length(arr_2, len(arr))
elif len(arr) < len(arr_2):
    arr = change_length(arr, len(arr_2))

result = [0 for i in range(len(arr) + 1)] # 结果最多是最长数的长度加1
k = 0 # 进位
for i in range(len(arr)):
    rs = k + int(arr[len(arr) - i - 1]) + int(arr_2[len(arr_2) - i - 1]) # 从个位开始加，同时加上进位
    result[len(arr) - i] = rs % 10
    k = 0
    if rs >= 10:
        k = int(rs / 10)

if k != 0: # k != 0 则最高位为k
    result[0] = k
    for i in range(len(result) - 1):
        print(result[i], end='')
    print(result[-1])
else: # 否则最高为为0不输出
    for i in range(len(result) - 2):
        print(result[i+1], end='')
    print(result[-1])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

2.16 哈夫曼树

问题描述
　　Huffman树在编码中有着广泛的应用。在这里，我们只关心Huffman树的构造过程。
　　给出一列数{pi}={p0, p1, …, pn-1}，用这列数构造Huffman树的过程如下：
　　1. 找到{pi}中最小的两个数，设为pa和pb，将pa和pb从{pi}中删除掉，然后将它们的和加入到{pi}中。这个过程的费用记为pa + pb。
　　2. 重复步骤1，直到{pi}中只剩下一个数。
　　在上面的操作过程中，把所有的费用相加，就得到了构造Huffman树的总费用。
　　本题任务：对于给定的一个数列，现在请你求出用该数列构造Huffman树的总费用。

例如，对于数列{pi}={5, 3, 8, 2, 9}，Huffman树的构造过程如下：
　　1. 找到{5, 3, 8, 2, 9}中最小的两个数，分别是2和3，从{pi}中删除它们并将和5加入，得到{5, 8, 9, 5}，费用为5。
　　2. 找到{5, 8, 9, 5}中最小的两个数，分别是5和5，从{pi}中删除它们并将和10加入，得到{8, 9, 10}，费用为10。
　　3. 找到{8, 9, 10}中最小的两个数，分别是8和9，从{pi}中删除它们并将和17加入，得到{10, 17}，费用为17。
　　4. 找到{10, 17}中最小的两个数，分别是10和17，从{pi}中删除它们并将和27加入，得到{27}，费用为27。
　　5. 现在，数列中只剩下一个数27，构造过程结束，总费用为5+10+17+27=59。
输入格式
　　输入的第一行包含一个正整数n（n<=100）。
　　接下来是n个正整数，表示p0, p1, …, pn-1，每个数不超过1000。
输出格式
　　输出用这些数构造Huffman树的总费用。
样例输入
5
5 3 8 2 9
样例输出
59

n = int(input())

arr = list(map(int, input().split()))

price = [0 for i in range(n - 1)]

for i in range(n - 1):
    arr.sort()
    # print(arr)
    value = arr.pop(0)
    value_2 = arr.pop(0)
    price[i] = value + value_2
    arr.append(price[i])

print(sum(price))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

2.17 N皇后问题

要在n*n的国际象棋棋盘中放n个皇后，使任意两个皇后都不能互相吃掉。规则：皇后能吃掉同一行、同一列、同一对角线的任意棋子。求所有的解。n=8是就是著名的八皇后问题了。

def queen(A, cur=0):
	# 递归回溯思想解决n皇后问题
    if cur == len(A): # 所有的皇后都正确放置完毕，输出每个皇后所在的位置
        print(A)
        return 0
    for col in range(len(A)):
        A[cur], flag = col, True
        for row in range(cur): # 检测本次所放皇后的位置是否在同行同列或同一对角线上
            if A[row] == col or abs(col - A[row]) == cur - row: # 是的话，该位置不能放，向上回溯
                flag = False
                break
        if flag: # 否的话，继续放下一个皇后
            queen(A, cur+1)


n = int(input()) # n为8，就是著名的八皇后问题啦

queen([None] * n)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

2.18 报时助手

问题描述
　　给定当前的时间，请用英文的读法将它读出来。
　　时间用时h和分m表示，在英文的读法中，读一个时间的方法是：
　　如果m为0，则将时读出来，然后加上“o’clock”，如3:00读作“three o’clock”。
　　如果m不为0，则将时读出来，然后将分读出来，如5:30读作“five thirty”。
　　时和分的读法使用的是英文数字的读法，其中0~20读作：
　　0:zero, 1: one, 2:two, 3:three, 4:four, 5:five, 6:six, 7:seven, 8:eight, 9:nine, 10:ten, 11:eleven, 12:twelve, 13:thirteen, 14:fourteen, 15:fifteen, 16:sixteen, 17:seventeen, 18:eighteen, 19:nineteen, 20:twenty。
　　30读作thirty，40读作forty，50读作fifty。
　　对于大于20小于60的数字，首先读整十的数，然后再加上个位数。如31首先读30再加1的读法，读作“thirty one”。
　　按上面的规则21:54读作“twenty one fifty four”，9:07读作“nine seven”，0:15读作“zero fifteen”。
输入格式
　　输入包含两个非负整数h和m，表示时间的时和分。非零的数字前没有前导0。h小于24，m小于60。
输出格式
　　输出时间时刻的英文。
样例输入
0 15
样例输出
zero fifteen

h, m = map(int, input().split())

time = {0: 'zero', 1: 'one', 2: 'two', 3: 'three', 4: 'four', 5: 'five', 6: 'six', 7: 'seven', 8: 'eight', 9: 'nine',
        10: 'ten', 11: 'eleven', 12: 'twelve', 13: 'thirteen', 14: 'fourteen', 15: 'fifteen', 16: 'sixteen',
        17: 'seventeen', 18: 'eighteen', 19: 'nineteen', 20: 'twenty', 21: 'twenty one', 22: 'twenty two',
        23: 'twenty three', 30: 'thirty', 40: 'forty', 50: 'fifty'}
        # 其实21，22，23可以不加入字典中，但为了后边小时略去判断简化代码，直接加在字典中，方便后边直接输出小时

if m == 0:
    print(time[h] + ' o\'clock')
else:
    print(time[h], end=' ')
    if 0 < m <= 20 or m == 30 or m == 40 or m == 50:
        print(time[m])
    elif 20 < m < 30:
        print(time[20] + ' ' + time[m - 20])
    elif 30 < m < 40:
        print(time[30] + ' ' + time[m - 30])
    elif 40 < m < 50:
        print(time[40] + ' ' + time[m - 40])
    else:
        print(time[50] + ' ' + time[m - 50])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

2.19 回形取数

问题描述
　　回形取数就是沿矩阵的边取数，若当前方向上无数可取或已经取过，则左转90度。一开始位于矩阵左上角，方向向下。
输入格式
　　输入第一行是两个不超过200的正整数m, n，表示矩阵的行和列。接下来m行每行n个整数，表示这个矩阵。
输出格式
　　输出只有一行，共mn个数，为输入矩阵回形取数得到的结果。数之间用一个空格分隔，行末不要有多余的空格。
样例输入
3 3
1 2 3
4 5 6
7 8 9
样例输出
1 4 7 8 9 6 3 2 5
样例输入
3 2
1 2
3 4
5 6
样例输出
1 3 5 6 4 2
注意

行末要求不要有多余的空格，不知意思是一个空格也不能有还是只可以有一个空格，由于控制最后一个数的输出很麻烦，这里博主在行末输出了一个空格，提交蓝桥系统100分通过
另外，读者们可以尝试去寻找最后一个数的输出位置规律，使得最后一个数单独输出，这样就无空格啦，这里博主有时间的话回去再尝试，然后会发出相应代码，敬请期待。

m, n = map(int, input().split())
row = col = count = 0
matrix = [[] for _ in range(m)]

for i in range(m):
    arr = input().split()
    for j in range(n):
        matrix[i].append(int(arr[j]))

while count < m * n:  # 总共m*n个数
    while row < m and matrix[row][col] != -1:  # 向下取数
        print(matrix[row][col], end=' ')
        matrix[row][col] = -1  # 将去过的位置置为-1
        row += 1
        count += 1
    row -= 1  # 上个循环结束后row的值为m,需要减1，否则越界
    col += 1  # 列值加1，因为第零列在上个循环已经输出，往右推一行
    while col < n and matrix[row][col] != -1:  # 向右取数
        print(matrix[row][col], end=' ')
        matrix[row][col] = -1  # 将去过的位置置为-1
        col += 1
        count += 1
    row -= 1  # 往上推一行
    col -= 1  # 上个循环使列值为n
    while row >= 0 and matrix[row][col] != -1:  # 向上取数
        print(matrix[row][col], end=' ')
        matrix[row][col] = -1  # 将去过的位置置为-1
        row -= 1
        count += 1
    row += 1  # 上个循环使行值为-1
    col -= 1  # 往左推一行
    while col >= 0 and matrix[row][col] != -1:  # 向左取数
        print(matrix[row][col], end=' ')
        matrix[row][col] = -1  # 将去过的位置置为-1
        col -= 1
        count += 1
    col += 1  # 上个循环使列值为-1
    row += 1  # 向下推一行
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

2.20 龟兔赛跑预测

问题描述
　　话说这个世界上有各种各样的兔子和乌龟，但是研究发现，所有的兔子和乌龟都有一个共同的特点——喜欢赛跑。于是世界上各个角落都不断在发生着乌龟和兔子的比赛，小华对此很感兴趣，于是决定研究不同兔子和乌龟的赛跑。他发现，兔子虽然跑比乌龟快，但它们有众所周知的毛病——骄傲且懒惰，于是在与乌龟的比赛中，一旦任一秒结束后兔子发现自己领先t米或以上，它们就会停下来休息s秒。对于不同的兔子，t，s的数值是不同的，但是所有的乌龟却是一致——它们不到终点决不停止。
　　然而有些比赛相当漫长，全程观看会耗费大量时间，而小华发现只要在每场比赛开始后记录下兔子和乌龟的数据——兔子的速度v1（表示每秒兔子能跑v1米），乌龟的速度v2，以及兔子对应的t，s值，以及赛道的长度l——就能预测出比赛的结果。但是小华很懒，不想通过手工计算推测出比赛的结果，于是他找到了你——清华大学计算机系的高才生——请求帮助，请你写一个程序，对于输入的一场比赛的数据v1，v2，t，s，l，预测该场比赛的结果。
输入格式
　　输入只有一行，包含用空格隔开的五个正整数v1，v2，t，s，l，其中(v1,v2<=100;t<=300;s<=10;l<=10000且为v1,v2的公倍数)
输出格式
　　输出包含两行，第一行输出比赛结果——一个大写字母“T”或“R”或“D”，分别表示乌龟获胜，兔子获胜，或者两者同时到达终点。
　　第二行输出一个正整数，表示获胜者（或者双方同时）到达终点所耗费的时间（秒数）。
样例输入
10 5 5 2 20
样例输出
D
4
样例输入
10 5 5 1 20
样例输出
R
3
样例输入
10 5 5 3 20
样例输出
T
4

data = list(map(int, input().split()))

rabbit = tortoise = time = 0

flag = False

while True:
    if rabbit == data[-1] or tortoise == data[-1]:  # 如果兔子或乌龟到达终点，结束
        break
    if rabbit - tortoise >= data[2]:  # 兔子达到领先条件，休息
        for i in range(data[3]):  # 休息时间按秒增加，乌龟路程按秒增加
            tortoise += data[1]
            time += 1
            if tortoise == data[-1]:  # 兔子休息时，乌龟到达了终点，结束。
                # 注意：有可能兔子在休息中，乌龟就到达了终点
                # 所以休息时间未必循环完
                # 如：兔子要休息10s，乌龟可能在兔子休息的第9s就到达了终点
                # 这里的flag就起到提前结束的功能
                flag = True
                break
        if flag:  # 如果提前结束，则全部结束
            break
    time += 1  # 每走一秒，兔子和乌龟按相应速度增加相应距离
    rabbit += data[0]
    tortoise += data[1]


if rabbit > tortoise:  # 谁先到达终点，谁的距离大
    print('R')
    print(time)
elif rabbit < tortoise:
    print('T')
    print(time)
else:  # 相等则平局
    print('D')
    print(time)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

2.21 芯片测试

问题描述
　　有n（2≤n≤20）块芯片，有好有坏，已知好芯片比坏芯片多。
　　每个芯片都能用来测试其他芯片。用好芯片测试其他芯片时，能正确给出被测试芯片是好还是坏。而用坏芯片测试其他芯片时，会随机给出好或是坏的测试结果（即此结果与被测试芯片实际的好坏无关）。
　　给出所有芯片的测试结果，问哪些芯片是好芯片。
输入格式
　　输入数据第一行为一个整数n，表示芯片个数。
　　第二行到第n+1行为n*n的一张表，每行n个数据。表中的每个数据为0或1，在这n行中的第i行第j列（1≤i, j≤n）的数据表示用第i块芯片测试第j块芯片时得到的测试结果，1表示好，0表示坏，i=j时一律为1（并不表示该芯片对本身的测试结果。芯片不能对本身进行测试）。
输出格式
　　按从小到大的顺序输出所有好芯片的编号
样例输入
3
1 0 1
0 1 0
1 0 1
样例输出
1 3
解题思路：

重点是好芯片比坏芯片多
如果忽略这个问题就很难解决，本人开始你就不幸忽略了。。。
既然好芯片比坏芯片多，那么我们只需记录每一列0的个数就行了，若个数超过n/2，则此芯片为坏芯片
一个chip列表来记录芯片的好坏

n = int(input())

arr = [[] for _ in range(n)]

chip = [True for _ in range(n)]

for i in range(n):
    arr_ = input().split()
    for j in range(n):
        arr[i].append(int(arr_[j]))

for i in range(n):
    count = 0
    for j in range(n):
        if arr[j][i] == 0:
            count += 1
    if count > n / 2:
        chip[i] = False

for i in range(n):
    if chip[i]:
        print(i + 1, end=' ')
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

2.22 FJ字符串

问题描述
　　FJ在沙盘上写了这样一些字符串：
　　A1 = “A”
　　A2 = “ABA”
　　A3 = “ABACABA”
　　A4 = “ABACABADABACABA”
　　… …
　　你能找出其中的规律并写所有的数列AN吗？
输入格式
　　仅有一个数：N ≤ 26。
输出格式
　　请输出相应的字符串AN，以一个换行符结束。输出中不得含有多余的空格或换行、回车符。
样例输入
3
样例输出
ABACABA

n = int(input())

str_n = ''

for i in range(n):
    str_n = str_n + chr(ord('A') + i) + str_n

print(str_n)
1
2
3
4
5
6
7
8

2.23 sin之舞

问题描述
　　最近FJ为他的奶牛们开设了数学分析课，FJ知道若要学好这门课，必须有一个好的三角函数基本功。所以他准备和奶牛们做一个“Sine之舞”的游戏，寓教于乐，提高奶牛们的计算能力。
　　不妨设
　　An=sin(1–sin(2+sin(3–sin(4+…sin(n))…)
　　Sn=(…(A1+n)A2+n-1)A3+…+2)An+1
　　FJ想让奶牛们计算Sn的值，请你帮助FJ打印出Sn的完整表达式，以方便奶牛们做题。
输入格式
　　仅有一个数：N<201。
输出格式
　　请输出相应的表达式Sn，以一个换行符结束。输出中不得含有多余的空格或换行、回车符。
样例输入
3
样例输出
((sin(1)+3)sin(1–sin(2))+2)sin(1–sin(2+sin(3)))+1
解题思路：

这里主要运用到递归的思想
先递归求An
然后求Sn
Sn通用过调用An求出

def A(n, k):

    if n == k:
        return

    print('sin(%d' % (n + 1), end='')

    if n + 1 != k:  # 若后边还有式子，判断是输出+号还是-号
        if n % 2 == 1:
            print('+', end='')
        else:
            print('-', end='')
    else:  # 若后边没有式子，输出右括号结束
        # 注意，这里只输出最后一次的右括号，前边左括号对应的右括号在S()函数中补全
        print(')', end='')

    n += 1

    A(n, k)  # 递归调用自身


def S(n):

    k = t = 1

    if n == 0:
        return

    for i in range(n - 1):
        print('(', end='')

    while n != 0:
        A(0, k)
        for i in range(t - 1):  # 不全A()函数中的括号
            print(')', end='')
        print('+%d' % n, end='')
        if n != 1:  # 最后一项加完整数之和不必再输出右括号
            print(')', end='')
        k += 1
        t += 1
        n -= 1


n = int(input())

# A(0, 3)

S(n)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

2.24 数的读法

问题描述
　　Tom教授正在给研究生讲授一门关于基因的课程，有一件事情让他颇为头疼：一条染色体上有成千上万个碱基对，它们从0开始编号，到几百万，几千万，甚至上亿。
　　比如说，在对学生讲解第1234567009号位置上的碱基时，光看着数字是很难准确的念出来的。
　　所以，他迫切地需要一个系统，然后当他输入12 3456 7009时，会给出相应的念法：
　　十二亿三千四百五十六万七千零九
　　用汉语拼音表示为
　　shi er yi san qian si bai wu shi liu wan qi qian ling jiu
　　这样他只需要照着念就可以了。
　　你的任务是帮他设计这样一个系统：给定一个阿拉伯数字串，你帮他按照中文读写的规范转为汉语拼音字串，相邻的两个音节用一个空格符格开。
　　注意必须严格按照规范，比如说“10010”读作“yi wan ling yi shi”而不是“yi wan ling shi”，“100000”读作“shi wan”而不是“yi shi wan”，“2000”读作“er qian”而不是“liang qian”。
输入格式
　　有一个数字串，数值大小不超过2,000,000,000。
输出格式
　　是一个由小写英文字母，逗号和空格组成的字符串，表示该数的英文读法。
样例输入
1234567009
样例输出
shi er yi san qian si bai wu shi liu wan qi qian ling jiu
解题思路：

开始我按位置一位一位读，读到1万代码就开始很复杂了，所以考虑一定有相应读法的规律
利用循环来搞定，苦思冥想之后，还是利用度娘，一下就清晰了。。。
首先，读一个数，要处理开头为1的位置要不要读的问题
其次就是，处理多个连续0的读法问题
处理1的代码块下方已注释
就是不要把11，读作yi shi yi,111111不要读作yi shi yi wan yi qian yi bai yi shi yi
处理0的连续问题代码块中也给与了注释
就是10001不要读作yi wan ling ling ling ling yi,而是yi wan ling yi
参考以下代码

n = input()

pin_yin = {'0': 'ling', '1': 'yi', '2': 'er', '3': 'san', '4': 'si', '5': 'wu',
           '6': 'liu', '7': 'qi', '8': 'ba', '9': 'jiu'}
pin_yin_2 = {0: '', 1: '', 2: 'shi', 3: 'bai', 4: 'qian', 5: 'wan', 6: 'shi',
             7: 'bai', 8: 'qian', 9: 'yi', 10: 'shi'}
n = n + ' '

l = len(n) - 1

for i in range(l):
    j = int(n[i])
    if j != 0:  # 不为0时的读法
        if (l - i == 2 or l - i == 6 or l - i == 10) and j == 1:
            # 在十位，十万位，十亿位置且位于开头的1不读
            # 例子：
            # 1111111111 会读出 yi shi yi yi yi qian yi bai yi shi yi wan yi qian yi bai yi shi yi
            # 111111 会读出 yi shi yi wan yi qian yi bai yi shi yi
            # 11 会读出 yi shi yi
            # 加上此约束后，则不会读出开头的 yi
            if i != 0:  # 第一个1不输出1， 若不添加此条件，12会读出 yi shi er
                print(pin_yin['1'], end=' ')
            print(pin_yin_2[2], end=' ')
            continue
        print(pin_yin[n[i]], end=' ')
        print(pin_yin_2[l - i], end=' ')
    else:  # 处理0的读法问题
        if l - i == 5 or l - i == 9:  # 如果此0是在万位或亿位，则读出万或亿
            print(pin_yin_2[l - i], end=' ')
        if n[i + 1] == '0' or i == l - 1:  # 如果后一位仍然为0，或者，当前是最后以为，则不读此0
            continue
        print(pin_yin['0'], end=' ')  # 否则才读出这个零
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

2.25 完美的代价

问题描述
　　回文串，是一种特殊的字符串，它从左往右读和从右往左读是一样的。小龙龙认为回文串才是完美的。现在给你一个串，它不一定是回文的，请你计算最少的交换次数使得该串变成一个完美的回文串。
　　交换的定义是：交换两个相邻的字符
　　例如mamad
　　第一次交换 ad : mamda
　　第二次交换 md : madma
　　第三次交换 ma : madam (回文！完美！)
输入格式
　　第一行是一个整数N，表示接下来的字符串的长度(N <= 8000)
　　第二行是一个字符串，长度为N.只包含小写字母
输出格式
　　如果可能，输出最少的交换次数。
　　否则输出Impossible
样例输入
5
mamad
样例输出
3
解题思路

两种情况：
1.impossible的情况：如果有一个字符出现的次数是奇数次数，而且n是偶数，那么不可能构成回文。
如果n是奇数，但是已经有一个字符出现的次数是奇数次数了，那么如果又有一个字符是奇数次数，就不可能构成回文。
2.如果n是奇数，计算中间那个字符交换的次数的时候，不需要模拟把这个数移动到中间去，因为移动到中间的话假设有一对数都在左边或者都在右边。那么交换成回文的时候就要经过中间，就会每次把cnt多加了1，而这个1是没有必要的，因为可以所有的回文移动完了之后再把这个独立的奇数移动过去，才能保证交换次数最少。

例如：

此图片引用自博客：qq_40605470

n = int(input())

pal = list(input())

count = flag = 0  # count计数，flag判断是否已经有一个单独的奇个数的字符了

m = n - 1

for i in range(m):  # 从头遍历到倒数第二个字符
    for k in range(m, i - 1, -1):  # 从后面往前一直到i寻找和pal[i]相同的pal[k]
        if k == i:  # 如果找不到相同的
            if n % 2 == 0 or flag == 1:  # impossible的两种情况
                print('Impossible')
                exit()
            flag = 1
            count += int(n / 2) - i
        elif pal[k] == pal[i]:
            for j in range(k, m):  # 找到相同的，进行交换
                pal[j], pal[j + 1] = pal[j + 1], pal[j]
                count += 1  # 计数器加1
            m -= 1  # 最后拍好序的不在进行比较
            break

print(count)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

这个出现了之前遇到同样的问题，提交后十组测试数据，九组正确，但是有一组超时，不得分。但是同样的算法，C++版本的代码提交后完美通过，100分！目前不知道怎么办还，有明白的请不吝赐教，非常感谢。
C++版代码如下：

#include <iostream>
using namespace std;
int main() {
    int n;
    cin >> n;
    string s;
    cin >> s;
    int j = n - 1;
    int cnt = 0;//cnt用来统计交换的次数
    int flag = 0;//flag判断是否已经有一个单独的奇个数的字符了
    for(int i = 0; i < j; i++) {//i指针从头遍历到倒数第二个字符
        for(int k = j; k >= i; k--) {//k指针从后面往前一直到i寻找和s[i]相同的s[k]
            if(k == i) {//如果找不到相同的
                if(n % 2 == 0 || flag == 1) {//impossible的两种情况
                    cout << "Impossible";
                    return 0;
                }
                flag = 1;
                cnt += n / 2 - i;
            } else if(s[k] == s[i]) {
                for(int l = k; l < j; l++) {
                    swap(s[l], s[l+1]);//把s[k]换到s[j]处
                    cnt++;//统计交换次数
                }
                j--;
                break;
            }
        }
    }
    cout << cnt;
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

注：此代码完美通过！

2.26 矩形面积交

问题描述
　　平面上有两个矩形，它们的边平行于直角坐标系的X轴或Y轴。对于每个矩形，我们给出它的一对相对顶点的坐标，请你编程算出两个矩形的交的面积。
输入格式
　　输入仅包含两行，每行描述一个矩形。
　　在每行中，给出矩形的一对相对顶点的坐标，每个点的坐标都用两个绝对值不超过10^7的实数表示。
输出格式
　　输出仅包含一个实数，为交的面积，保留到小数后两位。
样例输入
1 1 3 3
2 2 4 4
样例输出
1.00
解题思路：

重点是找到两个矩形产生交集的条件
矩阵1的对角点坐标的横坐标取最小，矩阵2的对角点坐标的横坐标取最小，然后再从这两个值中取最大，得x1
矩阵1的对角点坐标的横坐标取最大，矩阵2的对角点坐标的横坐标取最大，然后再从这两个值中取最小，得x2
如果x1<x2，这两个矩形才会有交集
纵坐标同理
最后交集的面积就为：
area = (x2 - x1) * (y2 - y1)

rect_1 = list(map(float, input().split()))

rect_2 = list(map(float, input().split()))

area = 0

x1 = max(min(rect_1[0], rect_1[2]), min(rect_2[0], rect_2[2]))

y1 = max(min(rect_1[1], rect_1[3]), min(rect_2[1], rect_2[3]))

x2 = min(max(rect_1[0], rect_1[2]), max(rect_2[0], rect_2[2]))

y2 = min(max(rect_1[1], rect_1[3]), max(rect_2[1], rect_2[3]))


if x1 < x2 and y1 < y2:
    area = (x2 - x1) * (y2 - y1)
    print('%.2f' % area)
else:
    print('%.2f' % area)


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

2.27 矩阵乘法

问题描述
　　给定一个N阶矩阵A，输出A的M次幂（M是非负整数）
　　例如：
　　A =
　　1 2
　　3 4
　　A的2次幂
　　7 10
　　15 22
输入格式
　　第一行是一个正整数N、M（1<=N<=30, 0<=M<=5），表示矩阵A的阶数和要求的幂数
　　接下来N行，每行N个绝对值不超过10的非负整数，描述矩阵A的值
输出格式
　　输出共N行，每行N个整数，表示A的M次幂所对应的矩阵。相邻的数之间用一个空格隔开
样例输入
2 2
1 2
3 4
样例输出
7 10
15 22

注意：

1.不要忘记方阵的0次幂这一特殊情况，它的结果是人为定义的，为n阶单位阵。
2.博主的代码中矩阵乘法函数，是一个普遍适用的矩阵乘法函数，即不是两个方阵相乘也行，只要两矩阵满足矩阵乘法定理即可，相应解释已在代码块中给出。
3.若你在参加考试，则代码越简化越好，如这题的矩阵乘法函数，题中给的输入矩阵必为n阶方阵，所以写矩阵乘法的函数就只针对n阶方阵来写就好了，以降低出错率，相应代码请读者自行写出，以加深理解。

def multi_rect(rect_1, shape_1, rect_2, shape_2):
    """矩阵乘法
    :param rect_1: 矩阵A
    :param shape_1: 矩阵A的形状
    :param rect_2: 矩阵B
    :param shape_2: 矩阵B的形状
    :return: 两矩阵之积和积的矩阵形状
    """
    if shape_1[1] != shape_2[0]:
        return
    rect_ = [[0 for _ in range(shape_2[1])] for _ in range(shape_1[0])]
    shape_ = (shape_1[0], shape_2[1])
    for i in range(shape_1[0]):
        for k in range(shape_2[1]):
            for j in range(shape_1[1]):
                rect_[i][k] += rect_1[i][j] * rect_2[j][k]  # 矩阵乘法定义

    return rect_, shape_


n, m = map(int, input().split())

rect = [[] for _ in range(n)]

for i in range(n):
    arr = input().split()
    for j in range(n):
        rect[i].append(int(arr[j]))

result, shape = rect, (n, n)

if m == 0:  # 0次幂只有为方阵才有，此时result为n阶单位阵
    result = [[0 for _ in range(n)] for _ in range(n)]  # shape仍然为(n, n)
    for i in range(n):
        result[i][i] = 1
else:  # m不为0，计算它的m次幂
    for _ in range(m - 1):
        result, shape = multi_rect(rect, (n, n), result, shape)

for i in range(shape[0]):
    for j in range(shape[1]):
        print(result[i][j], end=' ')
    print()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

2.28 2n皇后问题

问题描述
　　给定一个n*n的棋盘，棋盘中有一些位置不能放皇后。现在要向棋盘中放入n个黑皇后和n个白皇后，使任意的两个黑皇后都不在同一行、同一列或同一条对角线上，任意的两个白皇后都不在同一行、同一列或同一条对角线上。问总共有多少种放法？n小于等于8。
输入格式
　　输入的第一行为一个整数n，表示棋盘的大小。
　　接下来n行，每行n个0或1的整数，如果一个整数为1，表示对应的位置可以放皇后，如果一个整数为0，表示对应的位置不可以放皇后。
输出格式
　　输出一个整数，表示总共有多少种放法。
样例输入
4
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1
样例输出
2
样例输入
4
1 0 1 1
1 1 1 1
1 1 1 1
1 1 1 1
样例输出
0

前面2.17简单介绍了N皇后问题，这里的题目为2n皇后问题，就是先放置好白皇后，然后再不冲突的情况下按上述规则放置黑皇后
例2.17是网上给出的python版经典求解N皇后问题算法，此处作者自己查阅资料写了个N皇后问题代码，下方贴出，因为2n皇后问题求解是在此基础上求解的。

def n_queen(k):

    global count

    for i in range(k - 1):  # 判断是否可放置皇后的条件
        judge = queen[i] - queen[k - 1]
        if judge == 0 or abs(k - 1 - i) == abs(judge):
            return

    if k == n:
        print(queen)  # 输出皇后放置序列
        count += 1  # 解的个数
        return

    for i in range(n):  # 放置皇后
        queen[k] = i
        n_queen(k + 1)


count = 0

n = 4  # 此处的n为几，则为几皇后问题

queen = [0 for _ in range(n)]

n_queen(0)

print(count)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

下面给出2n皇后问题解的python代码，但是提交后十组测试数据有九组通过，一组运行超时，但结果也是正确的，同意的代码思想，改编为C语言版就能通过，而不会提示运行超时，这个问题遇到过不止一次了，一直不知道怎么解决，是在重新设计一个更快的算法才行吗，很苦恼。
同样算法思想写出的代码，python运行时间会比C,C++的运行时间长，从而导致提交python代码后结果为运行超时，而其他代码则完美通过。

python代码，得分83分，有一组数据运行超时。

def black_queen(k):

    global count

    for i in range(k - 1):
        judge = b_queen[i] - b_queen[k - 1]
        if judge == 0 or abs(k - 1 - i) == abs(judge):
            return

    if k == n:
        count += 1
        return

    for i in range(n):
        if i != w_queen[k] and chessboard[k][i] == 1:
            b_queen[k] = i
            black_queen(k + 1)


def white_queen(k):

    for i in range(k - 1):
        judge = w_queen[i] - w_queen[k - 1]
        if judge == 0 or abs(k - 1 - i) == abs(judge):
            return

    if k == n:
        black_queen(0)
        return

    for i in range(n):
        if chessboard[k][i] == 1:
            w_queen[k] = i
            white_queen(k + 1)


n = int(input())

count = 0

chessboard = [[] for _ in range(n)]

for i in range(n):
    arr = input().split()
    for j in range(n):
        chessboard[i].append(int(arr[j]))

w_queen = [0 for _ in range(n)]
b_queen = [0 for _ in range(n)]

white_queen(0)

print(count)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

C语言代码，100分。

#include<stdio.h>
 
#include<string.h>
 
#include<math.h>
 
#define MAXSIZE 1000
 
int bqueen[MAXSIZE];//黑皇后
 
int wqueen[MAXSIZE];//白皇后
 
int chessboard[MAXSIZE][MAXSIZE];//1:能放  0:不能放  
 
int count =0;
 
int n;
 
int BlackQueen(int k)
 
{
 
    int i;
 
    int j;
 
    for(i =0; i < k -1; i++)
 
    {
 
        int judge = bqueen[i]- bqueen[k -1];
 
        if(judge ==0|| fabs(k -1- i)== fabs(judge))
 
            return 0;
 
    }
 
    if(k == n)
 
    {
 
        count++;
 
        return 0;
 
    }
 
    for( j =0; j < n; j++)
 
    {
 
        if(j != wqueen[k]&& chessboard[k][j])
 
        {
 
            bqueen[k]= j;
 
            BlackQueen(k +1);
 
        }
 
       
 
    }
 
       
 
   
 
}
 
int WhiteQueen(int k)
 
{
 
    int i;
 
    int j;
 
    for( i =0; i < k -1; i++)
 
    {
 
        int judge = wqueen[i]- wqueen[k -1];
 
        if(judge ==0|| fabs(k -1- i)== fabs(judge))
 
            return 0;
 
    }
 
    if(k == n)
 
    {
 
        BlackQueen(0);
 
        return 0;
 
    }
 
    for( j =0; j < n; j++)
 
    {
 
        if(chessboard[k][j])
 
        {
 
            wqueen[k]= j;
 
            WhiteQueen(k +1);
 
        }
 
       
 
    }
 
       
 
       
 
}
 
 
 
int main(void)
 
{   int i;
 
    int j;
 
   // freopen("input3.txt","r",stdin);//这是我直接从文件中读取数据
 
    scanf("%d",&n);
 
    for(i =0; i < n; i++)
 
        for(j =0; j < n; j++)
 
        scanf("%d",&chessboard[i][j]);
 
    WhiteQueen(0);
 
    printf("%d\n",count);
 
    return 0;
 
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151

2.29 分解质因数

问题描述
　　求出区间[a,b]中所有整数的质因数分解。
输入格式
　　输入两个整数a，b。
输出格式
　　每行输出一个数的分解，形如k=a1a2a3…(a1<=a2<=a3…，k也是从小到大的)(具体可看样例)
样例输入
3 10
样例输出
3=3
4=22
5=5
6=23
7=7
8=222
9=33
10=25
提示
　　先筛出所有素数，然后再分解。
数据规模和约定
　　2<=a<=b<=10000
解题思路：

对一个数进行质因数分解
首先判断它本身是否为质数
是，则直接输出等于自身
否，进行循环，从2开始，输出最多的因数个数后才递增，这样保证不会有非质数因子
如，8 = 2 * 2 * 2
首先把最多的2输出，之后就不会出现2的倍数这样的因数啦。

又出现了同样的问题，python代码超时，C代码运行100分！好烦哦~
python代码

def is_prime(n):

    for i in range(2, n):
        if n % i == 0:
            return False

    return True


a, b = map(int, input().split())

for i in range(a, b + 1):
    if is_prime(i):  # 如果是素数，则等于它本身
        print(i, '=', i, sep='')
    else:
        print(i, '=', sep='', end='')
        temp = i
        j = 2
        while temp > 1:
            if temp % j == 0:  # 分解质因数，从j=2开始除,直到对i取余不为0时，才j += 1，保证每个j出现最多
                temp = int(temp / j)
                print(j, end='')
                if temp != 1:
                    print('*', end='')
            else:
                j += 1
        print()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

C语言代码

#include<iostream>

using namespace std;

bool issu(int n){ //判断素数 
	bool t = true;
	for(int i = 2;i <= n - 1;i++){
		if(n % i == 0){
			t = false;
			break;
		}
	}
	return t;
}

int main(){
	int a;
	int b;
	cin>>a>>b;
	for(int i = a;i <= b;i++){
		if(issu(i)){
			cout<<i<<"="<<i<<endl;
		}else{
			cout<<i<<"=";
			int tt = i;
			int j = 2;
			while(tt > 1){ //分解质因数，从i=2开始除,直到对i取余不为0时，才i++
							// 保证每个i出现最多 
				if(tt % j == 0){
					tt = tt / j;
					cout<<j;
					if(tt != 1){
						cout<<"*";
					}
				}else{
					j++;
				}
			}
			cout<<endl;
		}
	}
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

2.30 字符串对比

问题描述
　　给定两个仅由大写字母或小写字母组成的字符串(长度介于1到10之间)，它们之间的关系是以下4中情况之一：
　　1：两个字符串长度不等。比如 Beijing 和 Hebei
　　2：两个字符串不仅长度相等，而且相应位置上的字符完全一致(区分大小写)，比如 Beijing 和 Beijing
　　3：两个字符串长度相等，相应位置上的字符仅在不区分大小写的前提下才能达到完全一致（也就是说，它并不满足情况2）。比如 beijing 和 BEIjing
　　4：两个字符串长度相等，但是即使是不区分大小写也不能使这两个字符串一致。比如 Beijing 和 Nanjing
　　编程判断输入的两个字符串之间的关系属于这四类中的哪一类，给出所属的类的编号。
输入格式
　　包括两行，每行都是一个字符串
输出格式
　　仅有一个数字，表明这两个字符串的关系编号
样例输入
BEIjing

beiJing

样例输出
3

注意：

代码块中的upper函数也可以改为lower函数
就是样字符串中的英文字母全部改为大写或者小写

str_1 = input()

str_2 = input()

if len(str_1) != len(str_2):
    print(1)
elif str_1 == str_2:
    print(2)
elif str_1.upper() == str_2.upper():
    print(3)
else:
    print(4)
1
2
3
4
5
6
7
8
9
10
11
12

参考知识：

两个字符串处理函数
将字符串中字母全部改为大写的upper()函数
 将字符串中字母全部改为小写的lower()函数

2.31 时间转换

问题描述
　　给定一个以秒为单位的时间t，要求用H:M:S的格式来表示这个时间。H表示时间，M表示分钟，而S表示秒，它们都是整数且没有前导的“0”。例如，若t=0，则应输出是“0:0:0”；若t=3661，则输出“1:1:1”。
输入格式
　　输入只有一行，是一个整数t（0<=t<=86399）。
输出格式
　　输出只有一行，是以“H:M:S”的格式所表示的时间，不包括引号。
样例输入
0
样例输出
0:0:0
样例输入
5436
样例输出
1:30:36
解题思路：

这道题目就是单纯的把秒转换成小时和分钟，较为简单，不再赘述。

n = int(input())

h = int(n / 3600)

m = int((n - h * 3600) / 60)

s = int(n - h * 3600 - m * 60)

print(h, ':', m, ':', s, sep='')
1
2
3
4
5
6
7
8
9

3.提高篇

3.1 预测身高

问题描述：
　　生理卫生老师在课堂上娓娓道来：
　　你能看见你未来的样子吗？显然不能。但你能预测自己成年后的身高，有公式：
　　男孩成人后身高=（父亲身高+母亲身高）/21.08
　　女孩成人后身高=(父亲身高0.923+母亲身高）/2
　　数学老师听见了，回头说：这是大样本统计拟合公式，准确性不错。
　　生物老师听见了，回头说：结果不是绝对的，影响身高的因素很多，比如营养、疾病、体育锻炼、睡眠、情绪、环境因素等。
　　老师们齐回头，看见同学们都正在预测自己的身高。
　　毛老师见此情形，推推眼镜说：何必手算，编程又快又简单…
　　约定：
　　身高的单位用米表示，所以自然是会有小数的。
　　男性用整数1表示，女性用整数0表示。
　　预测的身高保留三位小数
输入格式
　　用空格分开的三个数，整数小数小数
　　分别表示：性别父亲身高母亲身高
输出格式
　　一个小数，表示根据上述表示预测的身高（保留三位小数）
样例输入
1 1.91 1.70
样例输出
1.949
样例输入
0 1.00 2.077
样例输出
1.500
数据规模和约定
　　父母身高范围（0，3]
　　时间限制1.0秒

随机从算法训练里抽取的一道题目，题干挺长，但是读完后发现太简单啦，不想发出来侮辱大家智商。但是做都做啦，就更新一下吧。。。

gender, father_height, mother_height = map(float, input().split())

if gender == 1:
    height = (father_height + mother_height) / 2 * 1.08
else:
    height = (father_height * 0.923 + mother_height) / 2

print('%.3f' % height)
1
2
3
4
5
6
7
8

3.2 最长滑雪道

问题描述
　　小袁非常喜欢滑雪，因为滑雪很刺激。为了获得速度，滑的区域必须向下倾斜，而且当你滑到坡底，你不得不再次走上坡或者等待升降机来载你。小袁想知道在某个区域中最长的一个滑坡。区域由一个二维数组给出。数组的每个数字代表点的高度。如下：
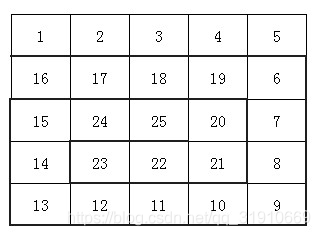
　　在这里插入图片描述
一个人可以从某个点滑向上下左右相邻四个点之一，当且仅当高度减小。在上面的例子中，一条可滑行的滑坡为24-17-16-1。当然25-24-23-…-3-2-1更长。事实上，这是最长的一条。
　　你的任务就是找到最长的一条滑坡，并且将滑坡的长度输出。滑坡的长度定义为经过点的个数，例如滑坡24-17-16-1的长度是4。
输入格式
　　输入的第一行表示区域的行数R和列数C(1<=R, C<=10)。下面是R行，每行有C个整数，依次是每个点的高度h（0<= h <=10000）。
输出格式
　　只有一行，为一个整数，即最长区域的长度。
样例输入
5 5
1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9
样例输出
25
解题思路：

1.偶然发现了一中二位数组输入的更简便方式：
arr = [list(map(int, input().split())) for _ in range(row)]
以后按二维数组的输入统统按此方法处理，前边已经写好的代码不再进行修改。
2.对于区域内每个点进行dfs，对每个点来说进行四个方向的dfs取最大值，然后取所有点为起点的最大长度的最大值，即为答案。
3.详细解释在代码块中相应位置给出。

def dfs(x, y):
    """
    深度递归搜索
    :param x: 横坐标
    :param y: 纵坐标
    :return: 最大距离
    """
    max_height = 1  # 初始距离为1
    if dp[x][y] > 0:  # 如果已经有了当前位置出发的最大距离，则直接返回
        return dp[x][y]
    for k in range(4):  # 判断该位置的上下左右四个位置
        tx = x + next_[k][0]
        ty = y + next_[k][1]
        if tx < 0 or tx >= row or ty < 0 or ty >= col:  # 越界情况
            continue
        if arr[tx][ty] >= arr[x][y]:  # 不符合高到低的情况
            continue
        max_height = max(max_height, dfs(tx, ty) + 1)  # 符合，递归搜索下一个位置且距离加1

    dp[x][y] = max_height  # 最终距离放在此矩阵中保存

    return dp[x][y]  # 返回该位置下的最大距离


row, col = map(int, input().split())

dp = [[0 for _ in range(col)] for _ in range(row)]  # 记录从每个位置(x, y)开始，它的最大长度

arr = [list(map(int, input().split())) for _ in range(row)]  # 这里发明了二位数组python输入方法的一种全新方式，偶然发现的

next_ = [[0, 1], [1, 0], [0, -1], [-1, 0]]  # 用来表示(x, y)的上下左右四个位置

ans = 0

for i in range(row):
    for j in range(col):
        ans = max(ans, dfs(i, j))

print(ans)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

3.3 K好数

资源限制
时间限制：1.0s 内存限制：256.0MB
问题描述

如果一个自然数N的K进制表示中任意的相邻的两位都不是相邻的数字，那么我们就说这个数是K好数。求L位K进制数中K好数的数目。例如K = 4，L = 2的时候，所有K好数为11、13、20、22、30、31、33 共7个。由于这个数目很大，请你输出它对1000000007取模后的值。
输入格式

输入包含两个正整数，K和L。
输出格式
输出一个整数，表示答案对1000000007取模后的值。
样例输入
4 2
样例输出
7
数据规模与约定

对于30%的数据，KL <= 106；

对于50%的数据，K <= 16， L <= 10；

对于100%的数据，1 <= K,L <= 100。

动态规划DP问题
“L位K进制数”：如：“2位4进制数”，它是指这个数是个两位数，其中个位数是4进制数（即从[0,3]中取一个数作为个位），十位数也是4进制数。同理，“3位7进制数”则指这个数是个3位数，其中个位、十位、百位都是7进制数。
K好数的要求：任意相邻的两位不是相邻的数字。
核心：dp[i][j]=dp[i][j]+dp[i-1][k]
当前位置的数总数=当前位置的数的数目+前一个位置的数的总数。

def count(length, kind, ans):
    for i in range(1, kind):
        dp[0][i] = 1
    for i in range(1, length):
        for j in range(kind):
            for k in range(kind):
                if abs(j - k) != 1:
                    if j - 1 == 0 and k == 0:  # 排除首位为0的情况
                        continue
                    dp[i][j] = dp[i][j]+dp[i-1][k]
                    dp[i][j] %= MOD
    for i in range(kind):
        ans += dp[length - 1][i]
        ans %= MOD
    return ans


K, L = map(int, input().split())

ans = 0

MOD = 1000000007

dp = [[0 for _ in range(max(L,K))] for _ in range(max(L,K))]

if K == 1 and L == 1:
    print(0)
elif K > 1 and L == 1:  # 1位的K进制的K好数总数就是K个
    print(K)
elif L > 1:
    print(count(L, K, ans))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

3.4 石子游戏

资源限制
时间限制：1.0s 内存限制：256.0MB
问题描述
　　石子游戏的规则如下：
　　地上有n堆石子，每次操作可选取两堆石子（石子个数分别为x和y）并将它们合并，操作的得分记为(x+1)×(y+1)，对地上的石子堆进行操作直到只剩下一堆石子时停止游戏。
　　请问在整个游戏过程中操作的总得分的最大值是多少？
输入格式
　　输入数据的第一行为整数n，表示地上的石子堆数；第二行至第n+1行是每堆石子的个数。
输出格式
　　程序输出一行，为游戏总得分的最大值。
样例输入
10
5105
19400
27309
19892
27814
25129
19272
12517
25419
4053
样例输出
15212676150
数据规模和约定
　　1≤n≤1000，1≤一堆中石子数≤50000

每次取最大的，符合贪心原则
这里直接排序，然后选取两个前二大数
计算结果，合并，删掉最后一个
列表长度不为1时循环
python的列表可以看作栈或队列

n = int(input())

result = 0

data = [int(input()) for _ in range(n)]

while len(data) != 1:
    data.sort()
    result += (data[-1] + 1) * (data[-2] + 1)
    data[-2] += data[-1]
    data.pop(-1)

print(result)
1
2
3
4
5
6
7
8
9
10
11
12
13

3.5 幸运顾客

资源限制
时间限制：2.0s 内存限制：256.0MB
　　为了吸引更多的顾客，某商场决定推行有奖抽彩活动。“本商场每日将产生一名幸运顾客，凡购买30元以上商品者均有机会获得本商场提供的一份精美礼品。”该商场的幸运顾客产生方式十分奇特：每位顾客可至抽奖台抽取一个幸运号码，该商场在抽奖活动推出的第i天将从所有顾客中（包括不在本日购物满30元者）挑出幸运号第i小的顾客作为当日的幸运顾客。该商场的商品本就价廉物美，自从有奖活动推出后，顾客更是络绎不绝，因此急需你编写一个程序，为他解决幸运顾客的产生问题。

【输入数据】
　　第1行一个整数N，表示命令数。
　　第2~N+1行，每行一个数，表示命令。如果x>=0，表示有一顾客抽取了号码x；如果x=-1，表示傍晚抽取该日的幸运号码。
【输出数据】
　　对应各命令-1输出幸运号码；每行一个号码。(两个相同的幸运号看作两个号码)
样例输入
6
3
4
-1
-1
3
-1
样例输出
3
4
4
解释
　　只关注获奖的号码是多少，每个号码可以获奖多次。
数据规模及约定
　　共10组数据。
　　对100%的数据，N=10^6所有命令为-1或int范围内的非负数，前i的命令中-1的数量不超过[i/2]（向下取整）。

很简单，不多说啦。

n = int(input())

arr = []
rs = []

ans = 0

for i in range(n):
    data = int(input())
    if data != -1:
        arr.append(data)
    else:
        arr.sort()
        rs.append(arr[ans])
        ans += 1

for i in range(len(rs)):
    print(rs[i])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

3.6 最长公共子序列（LCS）

资源限制
时间限制：1.0s 内存限制：256.0MB
问题描述
　　给定两个字符串，寻找这两个字串之间的最长公共子序列。
输入格式
　　输入两行，分别包含一个字符串，仅含有小写字母。
输出格式
　　最长公共子序列的长度。
样例输入
abcdgh
aedfhb
样例输出
3
样例说明
　　最长公共子序列为a，d，h。
数据规模和约定
　　字串长度1~1000。

动态规划问题，参考下面链接
最长公告子序列详解

def lcs(str_a, str_b):
    len_a = len(a)
    len_b = len(b)
    arr = [[0 for _ in range(len_b + 1)] for _ in range(len_a + 1)]
    for i in range(len_a + 1):
        for j in range(len_b + 1):
            if i == 0 or j == 0:
                arr[i][j] = 0
            elif i > 0 and j > 0 and str_a[i - 1] == str_b[j - 1]:
                arr[i][j] = arr[i - 1][j - 1] + 1
            else:
                arr[i][j] = max(arr[i][j - 1], arr[i - 1][j])
    return arr[len_a][len_b]


a = input()

b = input()

print(lcs(a, b))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

3.7 复数求和

资源限制
时间限制：1.0s 内存限制：512.0MB

从键盘读入n个复数（实部和虚部都为整数）用链表存储，遍历链表求出n个复数的和并输出。
样例输入:
3
3 4
5 2
1 3
样例输出:
9+9i

样例输入:
7
1 2
3 4
2 5
1 8
6 4
7 9
3 7
样例输出:
23+39i

列表中的元素是元组

n = int(input())

real = 0

imaginary = 0

com = [tuple(map(int, input().split())) for _ in range(n)]

for i in range(n):
    real += com[i][0]
    imaginary += com[i][1]

print(real, '+', imaginary, 'i', sep='')
1
2
3
4
5
6
7
8
9
10
11
12
13

3.8 成绩排名（结构体）

资源限制
时间限制：1.0s 内存限制：256.0MB
问题描述
　　小明刚经过了一次数学考试，老师由于忙碌忘记排名了，于是老师把这个光荣的任务交给了小明，小明则找到了聪明的你，希望你能帮他解决这个问题。
输入格式
　　第一行包含一个正整数N，表示有个人参加了考试。接下来N行，每行有一个字符串和一个正整数，分别表示人名和对应的成绩，用一个空格分隔。
输出格式
　　输出一共有N行，每行一个字符串，第i行的字符串表示成绩从高到低排在第i位的人的名字，若分数一样则按人名的字典序顺序从小到大。
样例输入
3
aaa 47
bbb 90
ccc 70
样例输出
bbb
ccc
aaa 【数据规模和约定】
人数<=100,分数<=100,人名仅包含小写字母。

主要是对排序函数的利用
sort()函数

n = int(input())

information = [tuple(input().split()) for _ in range(n)]

information.sort(key=lambda x: x[0])  # 先排姓名，按字母顺序

information.sort(key=lambda x: int(x[1]),reverse=True)  # 后排成绩，从大到小

for i in range(n):
    print(information[i][0])
1
2
3
4
5
6
7
8
9
10

3.9 递归倒置字符数组

资源限制
时间限制：1.0s 内存限制：512.0MB
问题描述
　　完成一个递归程序，倒置字符数组。并打印实现过程
　　递归逻辑为：
　　当字符长度等于1时，直接返回
　　否则，调换首尾两个字符，在递归地倒置字符数组的剩下部分
输入格式
　　字符数组长度及该数组
输出格式
　　在求解过程中，打印字符数组的变化情况。
　　最后空一行，在程序结尾处打印倒置后该数组的各个元素。
样例输入

Sample 1
5 abcde
Sample 2
1 a

样例输出

Sample 1
ebcda
edcba
edcba
Sample 2
a

有一点需要注意
字符串是不可变的，要想改变，需要把它强转为列表
再者，提醒一下
这个符号 // 是取商，这个符号 % 是求余
还有python中独有的二变量交换
a, b = b, a

n, s = input().split()
n = int(n)
s = list(s)
i = 0
while i < n // 2:
    s[i], s[n - i - 1] = s[n - i - 1], s[i]
    print(''.join(s))
    i += 1

print('\n'+''.join(s))
1
2
3
4
5
6
7
8
9
10

3.10 字符串跳步

资源限制
时间限制：1.0s 内存限制：256.0MB
问题描述
　　给定一个字符串，你需要从第start位开始每隔step位输出字符串对应位置上的字符。
输入格式
　　第一行一个只包含小写字母的字符串。

第二行两个非负整数start和step，意义见上。
输出格式
　　一行，表示对应输出。
样例输入
abcdefg
2 2
样例输出
ceg
数据规模和约定
　　start从0开始计数。
　　字符串长度不超过100000。

python如此简单

s = input()

start, step = map(int, input().split())

print(s[start: : step])
1
2
3
4
5

3.11 最长字符序列（同LCS）

资源限制
时间限制：1.0s 内存限制：256.0MB
　　最长字符序列
问题描述
　　设x(i), y(i), z(i)表示单个字符，则X={x(1)x(2)……x(m)}，Y={y(1)y(2)……y(n)}，Z={z(1)z(2)……z(k)},我们称其为字符序列，其中m,n和k分别是字符序列X，Y，Z的长度，括号()中的数字被称作字符序列的下标。
　　如果存在一个严格递增而且长度大于0的下标序列{i1,i2……ik}，使得对所有的j=1,2,……k，有x(ij)=z(j)，那么我们称Z是X的字符子序列。而且，如果Z既是X的字符子序列又是Y的字符子序列，那么我们称Z为X和Y的公共字符序列。
　　在我们今天的问题中，我们希望计算两个给定字符序列X和Y的最大长度的公共字符序列，这里我们只要求输出这个最大长度公共子序列对应的长度值。
　　举例来说，字符序列X=abcd，Y=acde，那么它们的最大长度为3，相应的公共字符序列为acd。
输入格式
　　输入一行，用空格隔开的两个字符串
输出格式
　　输出这两个字符序列对应的最大长度公共字符序列的长度值
样例输入
aAbB aabb
样例输出
2
数据规模和约定
　　输入字符串长度最长为100，区分大小写。

def lcs(str_a, str_b):
    len_a = len(a)
    len_b = len(b)
    arr = [[0 for _ in range(len_b + 1)] for _ in range(len_a + 1)]
    for i in range(len_a + 1):
        for j in range(len_b + 1):
            if i == 0 or j == 0:
                arr[i][j] = 0
            elif i > 0 and j > 0 and str_a[i - 1] == str_b[j - 1]:
                arr[i][j] = arr[i - 1][j - 1] + 1
            else:
                arr[i][j] = max(arr[i][j - 1], arr[i - 1][j])
    return arr[len_a][len_b]


a, b = input().split()

print(lcs(a, b))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

3.12 队列操作

问题描述
　　队列操作题。根据输入的操作命令，操作队列（1）入队、（2）出队并输出、（3）计算队中元素个数并输出。
输入格式
　　第一行一个数字N。
　　下面N行，每行第一个数字为操作命令（1）入队、（2）出队并输出、（3）计算队中元素个数并输出。
输出格式
　　若干行每行显示一个2或3命令的输出结果。注意：2.出队命令可能会出现空队出队（下溢），请输出“no”，并退出。
样例输入
7
1 19
1 56
2
3
2
3
2
样例输出
19
1
56
0
no
数据规模和约定
　　1<=N<=50

N = int(input())

queue = []

for _ in range(N):
    command = list(map(int, input().split()))
    if command[0] == 1:
        queue.append(command[1])
    elif command[0] == 2:
        if len(queue) == 0:
            print('no')
        else:
            print(queue[0])
            queue.pop(0)
    else:
        print(len(queue))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

3.13 字符串操作

问题描述
　　给出一个字符串和多行文字，在这些文字中找到字符串出现的那些行。你的程序还需支持大小写敏感选项：当选项打开时，表示同一个字母的大写和小写看作不同的字符；当选项关闭时，表示同一个字母的大写和小写看作相同的字符。
输入格式
　　输入的第一行包含一个字符串S，由大小写英文字母组成。
　　第二行包含一个数字，表示大小写敏感的选项，当数字为0时表示大小写不敏感，当数字为1时表示大小写敏感。
　　第三行包含一个整数n，表示给出的文字的行数。
　　接下来n行，每行包含一个字符串，字符串由大小写英文字母组成，不含空格和其他字符。
输出格式
　　输出多行，每行包含一个字符串，按出现的顺序依次给出那些包含了字符串S的行。
样例输入
Hello
1
5
HelloWorld
HiHiHelloHiHi
GrepIsAGreatTool
HELLO
HELLOisNOTHello
样例输出
HelloWorld
HiHiHelloHiHi
HELLOisNOTHello
样例说明
　　在上面的样例中，第四个字符串虽然也是Hello，但是大小写不正确。如果将输入的第二行改为0，则第四个字符串应该输出。
评测用例规模与约定
　　1<=n<=100，每个字符串的长度不超过100。

S = input()

alpha_switch = int(input())

n = int(input())

for _ in range(n):
    s_ = input()

    if alpha_switch == 1:
        if S in s_:
            print(s_)
    else:
        if S.upper() in s_.upper():
            print(s_)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

字符串大小写转换函数
字符串的find()、index()、rfind()、rindex()
参考地址

3.14 金陵十三钗

问题描述
　　在电影《金陵十三钗》中有十二个秦淮河的女人要自我牺牲代替十二个女学生去赴日本人的死亡宴会。为了不让日本人发现，自然需要一番乔装打扮。但由于天生材质的原因，每个人和每个人之间的相似度是不同的。由于我们这是编程题，因此情况就变成了金陵n钗。给出n个女人和n个学生的相似度矩阵，求她们之间的匹配所能获得的最大相似度。
　　所谓相似度矩阵是一个n*n的二维数组like[i][j]。其中i,j分别为女人的编号和学生的编号，皆从0到n-1编号。like[i][j]是一个0到100的整数值，表示第i个女人和第j个学生的相似度，值越大相似度越大，比如0表示完全不相似，100表示百分之百一样。每个女人都需要找一个自己代替的女学生。
　　最终要使两边一一配对，形成一个匹配。请编程找到一种匹配方案，使各对女人和女学生之间的相似度之和最大。
输入格式
　　第一行一个正整数n表示有n个秦淮河女人和n个女学生
　　接下来n行给出相似度，每行n个0到100的整数，依次对应二维矩阵的n行n列。
输出格式
　　仅一行，一个整数，表示可获得的最大相似度。
样例输入
4
97 91 68 14
8 33 27 92
36 32 98 53
73 7 17 82
样例输出
354
数据规模和约定
　　对于70%的数据，n<=10
　　对于100%的数据，n<=13
样例说明
　　最大相似度为91+92+98+73=354

n皇后弱化版

def queen(cur=0):
    global sum1, n
    if cur == n: # 所有的皇后都正确放置完毕，输出每个皇后所在的位置
        sum2 = 0
        for i in range(n):
            sum2 += a[i][b[i]]
        if sum2 > sum1:
            sum1 = sum2
        return 0

    for i in range(n):
        flag = True
        for j in range(cur): # 检测本次所放的位置是否在同行同列
            if b[j] == i: # 是的话，该位置不能放，向上回溯
                flag = False
                break
        if flag: # 否的话，继续放下一个
            b[cur] = i
            queen(cur+1)


n = int(input())

sum1 = 0

a = [list(map(int, input().split())) for _ in range(n)]

b = [0 for _ in range(n)]

queen()

print(sum1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

4.真题篇

待更新…

4.1不同子串

题目描述

    一个字符串的非空子串是指字符串中长度至少为 1 的连续的一段字符组成 的串。例如，字符串aaab 有非空子串a, b, aa, ab, aaa, aab, aaab，一共 7 个。 注意在计算时，只算本质不同的串的个数。
1

请问，字符串0100110001010001 有多少个不同的非空子串？

【答案提交】
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

这道题不难，大家都是能想到的应该。话不多说，直接上代码。

var = '0100110001010001' # var = 'aaab' 运行结果为7 表示算法正确
num = 1 # 自身也是1个，循环中没有去考虑他串本身，所以这里基数直接设置为1
sep = 1
var_n = []
while sep < len(var):
    var_n.append(var[0:sep])
    for i in range(len(var)-sep):  # 以sep为间隔依次向前推进，sep每轮循环增1
        if var[i+1:i+sep+1] in var_n:
            continue
        else:
            var_n.append(var[i+1:i+sep+1])
    sep += 1
    num += len(var_n)
    # print(var_n)
    var_n = []
print(num)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

运行结果
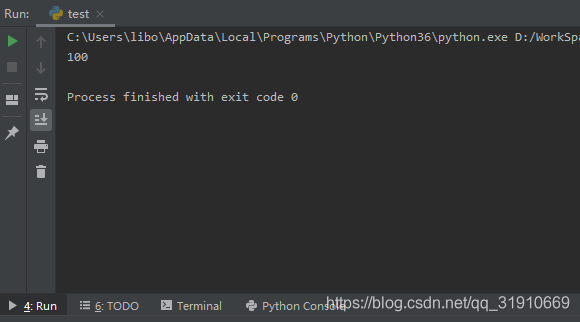
在这里插入图片描述
直接提交100就可以了。

4.2 年号字串

小明用字母A 对应数字1，B 对应2，以此类推，用Z 对应26。对于27
以上的数字，小明用两位或更长位的字符串来对应，例如AA 对应27，AB 对
应28，AZ 对应52，LQ 对应329。
请问2019 对应的字符串是什么？

实际上即为进制转换

"""
类似于进制转换，只是多了一步，把对应的字母换上
A~Z代表1~26，每26进1，27即为AA
17 77 Q
25 2 Y
2 0 B
BYQ
17 + 25 * 26 + 2 * 26 * 26 = 2019
"""

string = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'

ans = [0 for _ in range(5)]

index = 0

n = 2019

while n != 0:

    t = n % 26

    n = int(n / 26)

    ans[index] = string[t - 1]

    # print(t, n, ans[index])

    index += 1

for i in range(index - 1, -1, -1):

    print(ans[i], end='')
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

直接提交BYQ就可以啦。

4.3 数列求值

【问题描述】
给定数列 1, 1, 1, 3, 5, 9, 17, …，从第 4 项开始，每项都是前 3 项的和。求第 20190324 项的最后 4 位数字。
【答案提交】
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个 4 位整数（提示：答案的千位不为 0），在提交答案时只填写这个整数，填写多余的内容将无法得分。

只求后四位就可以啦

arr = [0 for _ in range(20190325)]

arr[0] = arr[1] = arr[2] = 1

for i in range(3, 20190324):

    arr[i] = (arr[i - 1] + arr[i - 2] + arr[i - 3]) % 10000

print(arr[20190323])
1
2
3
4
5
6
7
8
9

答案：4659

4.4 数的分解

【问题描述】

   把 2019 分解成 3 个各不相同的正整数之和，并且要求每个正整数都不包含数字 2 和 4，一共有多少种不同的分解方法？
1

注意交换 3 个整数的顺序被视为同一种方法，例如 1000+1001+18 和 1001+1000+18 被视为同一种。

【答案提交】

   这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一 个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

 
 
 
 1
1

count = 0


def check(x):

    while x != 0:
        t = x % 10
        x = int(x / 10)
        if t == 2 or t == 4:
            return False

    return True


for i in range(1, 2019):
    if check(i):
        for j in range(i + 1, 2019):
            if check(j):
                k = 2019 - i - j
                if k > j and check(k):
                    count += 1
                    print(i, j, k)

print(count)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

答案：40785

4.5 迷宫

在这里插入图片描述
数据

01010101001011001001010110010110100100001000101010
00001000100000101010010000100000001001100110100101
01111011010010001000001101001011100011000000010000
01000000001010100011010000101000001010101011001011
00011111000000101000010010100010100000101100000000
11001000110101000010101100011010011010101011110111
00011011010101001001001010000001000101001110000000
10100000101000100110101010111110011000010000111010
00111000001010100001100010000001000101001100001001
11000110100001110010001001010101010101010001101000
00010000100100000101001010101110100010101010000101
11100100101001001000010000010101010100100100010100
00000010000000101011001111010001100000101010100011
10101010011100001000011000010110011110110100001000
10101010100001101010100101000010100000111011101001
10000000101100010000101100101101001011100000000100
10101001000000010100100001000100000100011110101001
00101001010101101001010100011010101101110000110101
11001010000100001100000010100101000001000111000010
00001000110000110101101000000100101001001000011101
10100101000101000000001110110010110101101010100001
00101000010000110101010000100010001001000100010101
10100001000110010001000010101001010101011111010010
00000100101000000110010100101001000001000000000010
11010000001001110111001001000011101001011011101000
00000110100010001000100000001000011101000000110011
10101000101000100010001111100010101001010000001000
10000010100101001010110000000100101010001011101000
00111100001000010000000110111000000001000000001011
10000001100111010111010001000110111010101101111000
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

其他语言都为广度搜索，此方法类似，用队列来操作节点
此题为蓝桥练习系统的一道原题（非常类似，答案完全可以拿来直接用）：学霸的迷宫

class Node(object):  # 节点类
    def __init__(self, x, y, w):  # 添加类变量
        self.x = x
        self.y = y
        self.w = w

    def __str__(self):  # 类方法，调用此方法时返回w的内容
        return self.w


def up(node):
    return Node(node.x - 1, node.y, node.w+"U")  # 向上的情况


def down(node):
    return Node(node.x + 1, node.y, node.w+"D") # 向下的情况


def left(node):
    return Node(node.x, node.y - 1, node.w+"L")  # 向左的情况


def right(node):
    return Node(node.x, node.y + 1, node.w+"R")  # 向右的情况


if __name__ == '__main__':
    m, n = map(int, input().split())
    visited = set()  # 存储访问过的节点
    queue = []  # 首先建一个空队列用来存储访问的节点
    map_int = [[0] * (n + 1)]  # 第一行全置0
    for i in range(1, m+1):
        map_int.append([0]*(n+1))
        nums = input()  # 输入数据
        nums = "0" + nums  # 第一列全置0
        for j in range(0, n+1):
            map_int[i][j] = ord(nums[j]) - 48  # 把字符‘1’、‘0’转为数字
    # print(map_int)
    # exit()
    node = Node(1, 1, "")  # 开始位置节点
    queue.append(node)  # 放入队列
    while len(queue) != 0:  # 队不空时循环
        moveNode = queue[0]  # 移动节点
        queue.pop(0)  # 移动节点出队列
        moveStr = str(moveNode.x) + " "+ str(moveNode.y)  # 移动节点位置
        if moveStr not in visited:  # 移动节点若未访问
            visited.add(moveStr)  # 放入已访问节点列表
            if moveNode.x == m and moveNode.y == n:  # 到达最后位置时停止循环
                print(len(moveNode.__str__()))  # 输出步数，即长度
                print(moveNode)  # 输出路径
                break
            if moveNode.x < m:
                if map_int[moveNode.x + 1][moveNode.y] == 0:  # 向下的情况
                    queue.append(down(moveNode))
            if moveNode.y > 1:
                if map_int[moveNode.x][moveNode.y - 1] == 0:  # 向左的情况
                    queue.append(left(moveNode))
            if moveNode.y < n:
                if map_int[moveNode.x][moveNode.y + 1] == 0:  # 向右的情况
                    queue.append(right(moveNode))
            if moveNode.x > 1:
                if map_int[moveNode.x - 1][moveNode.y] == 0:  # 向上的情况
                    queue.append(up(moveNode))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63

python类的__str__方法

参考答案：
DDDDRRURRRRRRDRRRRDDDLDDRDDDDDDDDDDDDRDDRRRURRUURRDDDDRDRRRRRRDRRURRDDDRRRRUURUUUUUUULULLUUUURRRRUULLLUUUULLUUULUURRURRURURRRDDRRRRRDDRRDDLLLDDRRDDRDDLDDDLLDDLLLDLDDDLDDRRRRRRRRRDDDDDDRR
共186步

4.6 特别数的和

在这里插入图片描述

此题数据规模不大，直接暴力搜索解决就可以，较为简单

n = int(input())

s = 0

for i in range(1, n + 1):
    a = i
    while a != 0:
        temp = a % 10
        a = int(a / 10)
        if temp in [2, 0, 1, 9]:
            s += i
            falg = True
            break

print(s)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

4.7 完全二叉树的和

在这里插入图片描述
解题思路：

完全二叉树每一行的最后一个数的下标都是等于(2^n)-1
用deep表示当前深度，从当前这行的第一项加到最后一项然后和最大值max_sum比较。

n = int(input())

data = list(map(int, input().split()))

deep = flag_deep = 1

max_sum = 0

while 2 ** deep - 1 <= n:

    data_sum = sum(data[2 ** (deep - 1) - 1:(2 ** deep)])

    if max_sum < data_sum:

        max_sum = data_sum

        flag_deep = deep

    deep += 1

print(flag_deep)

# 一组测试数据
# 15
# 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
# 4
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

4.8 等差数列

在这里插入图片描述
解题思路：

先排序，然后找出等差数列的差值（各相邻数差值最小的），之后从所给数组的最小到最大开始循环，步长为所求的差值diff，利用count来计数

n = int(input())

data = list(map(int, input().split()))

count = 0

data.sort()

diff = float('inf')  # float('inf') 为无穷大，float('-inf') 为无穷小

for i in range(1, n):

    now_diff = data[i] - data[i - 1]

    if now_diff < diff:

        diff = now_diff

for i in range(data[0], data[-1], diff):

    count += 1

print(count + 1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

4.9 换钞票

x星球的钞票的面额只有：100元，5元，2元，1元，共4种。
小明去x星旅游，他手里只有2张100元的x星币，太不方便，恰好路过x星银行就去换零钱。
小明有点强迫症，他坚持要求200元换出的零钞中2元的张数刚好是1元的张数的10倍，
剩下的当然都是5元面额的。

银行的工作人员有点为难，你能帮助算出：在满足小明要求的前提下，最少要换给他多少张钞票吗？
（5元，2元，1元面额的必须都有，不能是0）

注意，需要提交的是一个整数，不要填写任何多余的内容。

for one in range(1,10):

    five = 0

    two = one * 10

    money = 200 - two * 2 - one

    if money % 5 == 0:

        five = money / 5

    count = one + two + five

    print(one, two, five, count)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

因为数目较小，很简单。这里代码直接列出了所有情况，运行结果如下：
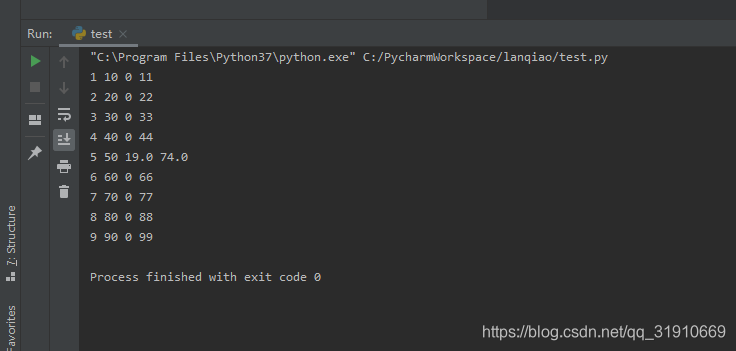
在这里插入图片描述
排除5元张数为0的情况就只剩下一种啦。
且结果为整数，则为74.

4.10 调手表

小明买了块高端大气上档次的电子手表，他正准备调时间呢。
在 M78 星云，时间的计量单位和地球上不同，M78 星云的一个小时有 n 分钟。
大家都知道，手表只有一个按钮可以把当前的数加一。在调分钟的时候，如果当前显示的数是 0 ，那么按一下按钮就会变成 1，再按一次变成 2 。如果当前的数是 n - 1，按一次后会变成 0 。
作为强迫症患者，小明一定要把手表的时间调对。如果手表上的时间比当前时间多1，则要按 n - 1 次加一按钮才能调回正确时间。
小明想，如果手表可以再添加一个按钮，表示把当前的数加 k 该多好啊……
他想知道，如果有了这个 +k 按钮，按照最优策略按键，从任意一个分钟数调到另外任意一个分钟数最多要按多少次。
注意，按 +k 按钮时，如果加k后数字超过n-1,则会对n取模。
比如，n=10, k=6 的时候，假设当前时间是0，连按2次 +k 按钮，则调为2。
「输入格式」
一行两个整数 n, k ，意义如题。
「输出格式」
一行一个整数
表示：按照最优策略按键，从一个时间调到另一个时间最多要按多少次。
「样例输入」
5 3
「样例输出」
2
「样例解释」
如果时间正确则按0次。否则要按的次数和操作系列之间的关系如下：
1：+1
2：+1, +1
3：+3
4：+3, +1
「数据范围」
对于 30% 的数据 0 < k < n <= 5
对于 60% 的数据 0 < k < n <= 100
对于 100% 的数据 0 < k < n <= 100000
资源约定：
峰值内存消耗（含虚拟机） < 256M
CPU消耗 < 1000ms
请严格按要求输出，不要画蛇添足地打印类似：“请您输入…” 的多余内容。
注意：
main函数需要返回0;
只使用ANSI C/ANSI C++ 标准;
不要调用依赖于编译环境或操作系统的特殊函数。
所有依赖的函数必须明确地在源文件中 #include
不能通过工程设置而省略常用头文件。
提交程序时，注意选择所期望的语言类型和编译器类型。

记住要求：
按照最优策略下的最多次数
开始我就困扰了，求成了最少次数
每次加1，遇到被整除的地方，原先的计数器置零，整除计数器加1
记录每次整除后的数值，求出最大的哪个数就是

n, k = map(int, input().split())

ans = []

count = count_ =0

for i in range(1, n):

    if i % k != 0:
        count += 1
    else:
        count = 0
        count_ += 1
    ans.append(count + count_)

print(max(ans))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

样例中的 5 3
对应的ans=[1, 2, 1, 2]
最大为2

比网上的其他df和bfs之类的要简单而且好理解的多

4.11 矩阵求和

经过重重笔试面试的考验，小明成功进入 Macrohard 公司工作。今天小明的任务是填满这么一张表：表有 n 行 n 列，行和列的编号都从1算起。其中第 i 行第 j 个元素的值是 gcd(i, j)的平方， gcd 表示最大公约数，以下是这个表的前四行的前四列： 1 1 1 1 1 4 1 4 1 1 9 1 1 4 1 16

小明突然冒出一个奇怪的想法，他想知道这张表中所有元素的和。由于表过于庞大，他希望借助计算机的力量。

「输入格式」一行一个正整数 n 意义见题。

「输出格式」一行一个数，表示所有元素的和。由于答案比较大，请输出模 (10^9 + 7)(即：十亿零七) 后的结果。

「样例输入」 4

「样例输出」 48

「数据范围」对于 30% 的数据，n <= 1000 存在 10% 的数据，n = 10^5 对于 60% 的数据，n <= 10^6 对于 100% 的数据，n <= 10^7

暴力求解是大家都会想到的，但是肯定会超时
这个题满分的话要用到数论的知识：欧拉函数+莫比乌斯反演。

暴力代码

def gcd(i, j):

    while j !=0:
        k = i % j
        i = j
        j = k

    return i


n = int(input())

sum_arr = 0

mod = 10 ** 9 + 7

for i in range(n):
    for j in range(n):
        t = gcd(i, j) ** 2
        sum_arr += t % mod

print(sum_arr)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

能得到一部分分数，考试时不会可以拿到一定的分数。

欧拉函数
 莫比乌斯反演
大家可以研究一下
下面给出代码

MOD = 10 ** 9 + 7

phi = []

sum_ = []

ans = 0


def euler_table(n):
    for _ in range(n + 1):
        phi.append(0)
        sum_.append(0)
    phi[1] = 1
    for i in range(2, n + 1):
        if phi[i] == 0:
            j = i
            while j <= n:
                if phi[j] == 0:
                    phi[j] = j
                phi[j] = int(phi[j] / i) * (i - 1)
                j += i
    sum_[1] = 1
    for i in range(2, n + 1):
        sum_[i] = sum_[i - 1] + phi[i] * 2


n = int(input())

euler_table(n)

for i in range(1, n + 1):
    ans = (ans + sum_[int(n / i)] * i % MOD * i % MOD) % MOD

print(ans)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

4.12 分数

标题：分数

1/1 + 1/2 + 1/4 + 1/8 + 1/16 + …
每项是前一项的一半，如果一共有20项,
求这个和是多少，结果用分数表示出来。
类似：
3/2
当然，这只是加了前2项而已。分子分母要求互质。

注意：
需要提交的是已经约分过的分数，中间任何位置不能含有空格。
请不要填写任何多余的文字或符号

求出分母，分子为2^19
用gcd函数通分

def gcd(a, b):

    while b != 0:
        c = a % b
        a = b
        b = c

    return a


molecule = 0

for i in range(20):
    molecule += 2 ** i

gc = gcd(molecule, 2 ** 19)

print(molecule // gc,'/',2 ** 19 // gc, sep='')
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

4.13 购物单

标题：购物单

小明刚刚找到工作，老板人很好，只是老板夫人很爱购物。老板忙的时候经常让小明帮忙到商场代为购物。小明很厌烦，但又不好推辞。

这不，XX大促销又来了！老板夫人开出了长长的购物单，都是有打折优惠的。
小明也有个怪癖，不到万不得已，从不刷卡，直接现金搞定。
现在小明很心烦，请你帮他计算一下，需要从取款机上取多少现金，才能搞定这次购物。

取款机只能提供100元面额的纸币。小明想尽可能少取些现金，够用就行了。
你的任务是计算出，小明最少需要取多少现金。
以下是让人头疼的购物单，为了保护隐私，``物品名称被隐藏了。

****     180.90       88折
****      10.25       65折
****      56.14        9折
****     104.65        9折
****     100.30       88折
****     297.15       半价
****      26.75       65折
****     130.62       半价
****     240.28       58折
****     270.62        8折
****     115.87       88折
****     247.34       95折
****      73.21        9折
****     101.00       半价
****      79.54       半价
****     278.44        7折
****     199.26       半价
****      12.97        9折
****     166.30       78折
****     125.50       58折
****      84.98        9折
****     113.35       68折
****     166.57       半价
****      42.56        9折
****      81.90       95折
****     131.78        8折
****     255.89       78折
****     109.17        9折
****     146.69       68折
****     139.33       65折
****     141.16       78折
****     154.74        8折
****      59.42        8折
****      85.44       68折
****     293.70       88折
****     261.79       65折
****      11.30       88折
****     268.27       58折
****     128.29       88折
****     251.03        8折
****     208.39       75折
****     128.88       75折
****      62.06        9折
****     225.87       75折
****      12.89       75折
****      34.28       75折
****      62.16       58折
****     129.12       半价
****     218.37       半价
****     289.69       8折
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

需要说明的是，88折指的是按标价的88%计算，而8折是按80%计算，余者类推。
特别地，半价是按50%计算。

请提交小明要从取款机上提取的金额，单位是元。
答案是一个整数，类似4300的样子，结尾必然是00，不要填写任何多余的内容。

特别提醒：不许携带计算器入场，也不能打开手机。

首先在把数据复制到记事本中
其次用Ctrl+H键替换
把****用空格替换
把7折、8折、9折替换为70、80、90
半价替换为50
其余折用空格替换
预处理后数据为

180.90  88  
 10.25  65  
 56.14   90  
104.65   90  
100.30  88  
297.15  50  
 26.75  65  
130.62  50  
240.28  58  
270.62   80  
115.87  88  
247.34  95  
 73.21   90  
101.00  50  
 79.54  50  
278.44   70  
199.26  50  
 12.97   90  
166.30  78  
125.50  58  
 84.98   90  
113.35  68  
166.57  50  
 42.56   90  
 81.90  95  
131.78   80  
255.89  78  
109.17   90  
146.69  68  
139.33  65  
141.16  78  
154.74   80  
 59.42   80  
 85.44  68  
293.70  88  
261.79  65  
 11.30  88  
268.27  58  
128.29  88  
251.03   80  
208.39  75  
128.88  75  
 62.06   90  
225.87  75  
 12.89  75  
 34.28  75  
 62.16  58  
129.12  50  
218.37  50  
289.69  80  
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

然后用代码计算就可以了

def result(s):
    return (float(s[0]) * float(s[1])) / 100


file = open('data.txt', 'r')

ans = 0

for line in file.readlines():
    s = line.split()
    ans += result(s)

file.close()

print(ans)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

运行后结果
5136.859500000001
所以最终答案为5200

4.14 等差素数列

2,3,5,7,11,13,…是素数序列。
类似：7,37,67,97,127,157 这样完全由素数组成的等差数列，叫等差素数数列。
上边的数列公差为30，长度为6。

2004年，格林与华人陶哲轩合作证明了：存在任意长度的素数等差数列。
这是数论领域一项惊人的成果！

有这一理论为基础，请你借助手中的计算机，满怀信心地搜索：

长度为10的等差素数列，其公差最小值是多少？

注意：需要提交的是一个整数，不要填写任何多余的内容和说明文字。

解释注释部分

def init_num():
    global tot
    for i in range(2, N):
        if dp[i] == 1:
            continue
        prim[tot] = i  # 记录N以内的所有素数
        tot += 1
        j = i
        while i * j < N:
            dp[i * j] = 1  # 不是素数的位置标记1
            j += 1


N = 1000010  # N的大小自己可以估计一下 想想也应该挺大的 多试几次

dp = [1, 1] + [ 0] * N

tot = 0

dif = 1

prim = [0] * N

init_num()

# print(dp[:100])
# print(prim[:100])

print(tot)

while dif * 10 < N:
    for j in range(tot):
        flag, temp = True, prim[j]
        for k in range(1, 10):  # temp后边是否再有9个满足等差条件的素数
            if temp + dif >= N or dp[temp + dif] == 1:
                flag = False
                break
            else:
                temp += dif
        if flag == True:
            print(dif, prim[j])
            exit()
    dif += 1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

运行结果
78499
210 199

解释：
N以内一共78499个素数
dif为210
起点199

十个数为：

dif_arr = [199]

dif = 210

for i in range(9):
    dif_arr.append(dif_arr[-1] + dif)

print(dif_arr)
1
2
3
4
5
6
7
8

[199, 409, 619, 829, 1039, 1249, 1459, 1669, 1879, 2089]

4.15 承压计算

X星球的高科技实验室中整齐地堆放着某批珍贵金属原料。

每块金属原料的外形、尺寸完全一致，但重量不同。
金属材料被严格地堆放成金字塔形。

                             7 
                            5 8 
                           7 8 8 
                          9 2 7 2 
                         8 1 4 9 1 
                        8 1 8 8 4 1 
                       7 9 6 1 4 5 4 
                      5 6 5 5 6 9 5 6 
                     5 5 4 7 9 3 5 5 1 
                    7 5 7 9 7 4 7 3 3 1 
                   4 6 4 5 5 8 8 3 2 4 3 
                  1 1 3 3 1 6 6 5 5 4 4 2 
                 9 9 9 2 1 9 1 9 2 9 5 7 9 
                4 3 3 7 7 9 3 6 1 3 8 8 3 7 
               3 6 8 1 5 3 9 5 8 3 8 1 8 3 3 
              8 3 2 3 3 5 5 8 5 4 2 8 6 7 6 9 
             8 1 8 1 8 4 6 2 2 1 7 9 4 2 3 3 4 
            2 8 4 2 2 9 9 2 8 3 4 9 6 3 9 4 6 9 
           7 9 7 4 9 7 6 6 2 8 9 4 1 8 1 7 2 1 6 
          9 2 8 6 4 2 7 9 5 4 1 2 5 1 7 3 9 8 3 3 
         5 2 1 6 7 9 3 2 8 9 5 5 6 6 6 2 1 8 7 9 9 
        6 7 1 8 8 7 5 3 6 5 4 7 3 4 6 7 8 1 3 2 7 4 
       2 2 6 3 5 3 4 9 2 4 5 7 6 6 3 2 7 2 4 8 5 5 4 
      7 4 4 5 8 3 3 8 1 8 6 3 2 1 6 2 6 4 6 3 8 2 9 6 
     1 2 4 1 3 3 5 3 4 9 6 3 8 6 5 9 1 5 3 2 6 8 8 5 3 
    2 2 7 9 3 3 2 8 6 9 8 4 4 9 5 8 2 6 3 4 8 4 9 3 8 8 
   7 7 7 9 7 5 2 7 9 2 5 1 9 2 6 5 3 9 3 5 7 3 5 4 2 8 9 
  7 7 6 6 8 7 5 5 8 2 4 7 7 4 7 2 6 9 2 1 8 2 9 8 5 7 3 6 
 5 9 4 5 5 7 5 5 6 3 5 3 9 5 8 9 5 4 1 2 6 1 4 3 5 3 2 4 1 
X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

其中的数字代表金属块的重量（计量单位较大）。
最下一层的X代表30台极高精度的电子秤。

假设每块原料的重量都十分精确地平均落在下方的两个金属块上，
最后，所有的金属块的重量都严格精确地平分落在最底层的电子秤上。
电子秤的计量单位很小，所以显示的数字很大。

工作人员发现，其中读数最小的电子秤的示数为：2086458231

请你推算出：读数最大的电子秤的示数为多少？

注意：需要提交的是一个整数，不要填写任何多余的内容。

把数据存到二维表里进行计算

arr = [[0] * 30 for _ in range(30)]

k = 0

file = open('data.txt', 'r')

for line in file.readlines():
    new_line = line.split()
    for i in range(len(new_line)):
        arr[k][i] = int(new_line[i])
    k += 1

for i in range(1, 30):
    for j in range(29):
        arr[i][j] += arr[i - 1][j] / 2
        arr[i][j + 1] += arr[i - 1][j] / 2

# print(min(arr[29]), max(arr[29]))

print(2086458231 / min(arr[29]) * max(arr[29]))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

接续篇传送门
Python解答蓝桥杯省赛真题之从入门到真题（续）

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/凡人多烦事01/article/detail/416348

Python解答蓝桥杯省赛真题之从入门到真题_蓝桥杯python题库及答案

文章目录

1.入门篇

1.1 Fibonacci数列题

1.2 入门训练 圆的面积

1.3 入门训练 序列求和

1.4 入门训练 A+B问题

2.基础篇

2.1 数列排序

2.2 十六进制转八进制

2.3 十六进制转十进制

2.4 十进制转十六进制

2.5 特殊回文数

2.6 回文数

2.7 水仙花数

2.8 杨辉三角

2.9 查找整数

2.10 数列特征

2.11 字母图形

2.12 字串01

2.13 闰年判断

2.14 阶乘计算

2.15 长整数加法

2.16 哈夫曼树

2.17 N皇后问题

2.18 报时助手

2.19 回形取数

2.20 龟兔赛跑预测

2.21 芯片测试

2.22 FJ字符串

2.23 sin之舞

2.24 数的读法

2.25 完美的代价

2.26 矩形面积交

2.27 矩阵乘法

2.28 2n皇后问题

2.29 分解质因数

2.30 字符串对比

2.31 时间转换

3.提高篇

3.1 预测身高

3.2 最长滑雪道

3.3 K好数

3.4 石子游戏

3.5 幸运顾客

3.6 最长公共子序列（LCS）

3.7 复数求和

3.8 成绩排名（结构体）

3.9 递归倒置字符数组

3.10 字符串跳步

3.11 最长字符序列（同LCS）

3.12 队列操作

3.13 字符串操作

3.14 金陵十三钗

4.真题篇

4.1不同子串

4.2 年号字串

4.3 数列求值

4.4 数的分解

4.5 迷宫

4.6 特别数的和

4.7 完全二叉树的和

4.8 等差数列

4.9 换钞票

4.10 调手表

4.11 矩阵求和

4.12 分数

4.13 购物单

4.14 等差素数列

4.15 承压计算

1.2 入门训练圆的面积

1.3 入门训练序列求和