C++：【数据结构】哈希表_c++哈希表

哈希表（hash table）又叫散列表，是一种很实用的数据结构。首先来看一下百度给出的定义：散列表，是根据关键码值(Key value)而直接进行访问的数据结构。也就是说，它通过把关键码值映射到表中一个位置来访问记录，以加快查找的速度。这个映射函数叫做散列函数，存放记录的数组叫做散列表。

通俗一点来说，就是我们有一堆值，他们的范围很大，但是又很分散，直接存储本身的话会非常占地方，所以我们就把它映射到一个较小的范围内，这样不但节省了空间，而且还方便查找。

举个例子就是，假设我们要存储 1000000000 、2000000 、17 这几个数，直接存的话就是开一个1000000000的数组，但是我们只用到了三个位置，有很多位置都浪费了，而且很占地方，运行着运行着就爆内存了。所以我们想一个解决办法，既然只有三个数，那我们不妨就开一个10的数组，把它们映射到10以内，比如2000000映射为2，所以就把2000000存储到位置2上；17映射为5，所以就把17存储到位置5上（不一定按大小顺序），然后我们想看看有没有这几个数的时候，只要映射一下，看看映射的位置有没有就好了。这样不但节省了很大的空间，而且还很方便能找到数据，因为只有十个位置。虽然多了一个麻烦的映射操作，但是比起哈希表的优点，这点小问题微不足道。

但是，这有一个显而易见的问题。如果不可避免地把俩数映射到了一个位置上面，那就需要特殊处理一下了。这种现象叫做哈希冲突，下面会详细解释怎么尽可能地避免哈希冲突，以及遇到后该如何解决这个问题。

一、对整数的哈希

先给出一道简单的模板题：acwing.模拟散列表

维护一个集合，支持如下几种操作：
I x，插入一个数 x；
Q x，询问数 x 是否在集合中出现过；
现在要进行 N 次操作，对于每个询问操作输出对应的结果。
输入格式
第一行包含整数 N，表示操作数量。
接下来 N 行，每行包含一个操作指令，操作指令为 I x，Q x 中的一种。
输出格式
对于每个询问指令 Q x，输出一个询问结果，如果 x 在集合中出现过，则输出 Yes，否则输出 No。
每个结果占一行。
数据范围
1≤N≤10⁵
−10⁹≤x≤10⁹
输入样例：

5
I 1
I 2
I 3
Q 2
Q 5

输出样例：

Yes
No

1.1、哈希函数

对整数数据的映射，叫整数哈希。

首先我们要设计一个哈希函数，也就是映射函数。当然这不用我们自己来设计，已经有被设计好的哈希方法并且是经过前人千锤百炼的，已经基本上没有什么错误的方法了。这里只介绍一种方法：除留余数法。说白了就是让数模上另一个数，以达到得到其映射位置的一个方法。那么我们要解决的就是模上谁这个问题了。

首先要模上的这个数是比较有讲究的，第一，模的这个数要是一个质数，这样可以极大地减少哈希冲突；第二，这个数要尽量离2的次幂远一点，这样进一步减少了哈希冲突的可能。
举个例子，我们假设数据的范围是 10^-9~10⁹（也即在32位和64位的编译器上int的“上下限”。在32位和64位编译器中，int占四个字节，即 -2147483648到2147483647，是10¹⁰级的），数据的个数至多是10⁵。正常情况下，我们会选择开一个 10⁵+10 的数组来存储数据，多一点空间为了防止越界，但是这里开数组就比较有讲究：首先要模上的数就是数组的长度，所以说，按理来说，应该取比数据数量大的第一个质数，这个要根据实际情况计算一下，这里算出来是100003，它离2的次方也很远。

同时要注意的是，因为数据中还存在负数，但是数组没有负的下标，所以我们要特殊处理一下。在C++中，对负数的取模就是对这个负数的绝对值取模再加个负号，所以操作很容易。但是其他语言要记得根据实际情况特殊处理一下。这样就得到了这个例子中的哈希函数：

const int N = 100003;

int hash(int x)
{
    //正常情况下应该是x % N，这是对包含负数情况的特殊操作
    return (x % N + N) % N;
}
1
2
3
4
5
6
7

通过这个函数，我们可以给定一个x，然后得到它对应的映射位置。

1.2、哈希冲突

解决了哈希函数，下一步就要详细解释怎么解决哈希冲突了。
解决哈希冲突的方式有很多种，这里只介绍两种主流的方式：拉链法和开放寻址法。

1.2.1、拉链法解决哈希冲突

正如其名，当遇到哈希冲突的时候，拉链法会在冲突的位置拉一条链来依次存放冲突的数据。举个例子，假设100被哈希到了4，那么这时候：

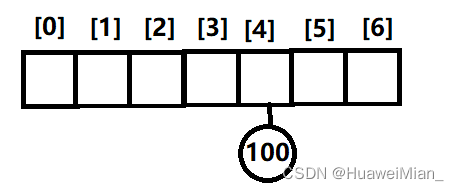
然后，24也被哈希到了4，所以我们就在100的基础上延长一下：

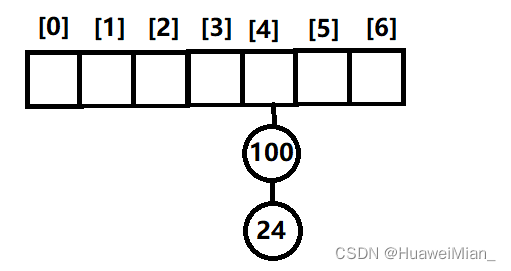
这样就解决了两个数的位置冲突的问题。不难想到，其实这就是链表嘛，只不过是好多条好多条链表。对数组模拟链表有疑问，可以参考我的这篇文章C++：【数据结构】用数组实现的单链表和双向链表。有了这个思路，实现起来就很容易了。这里给出例题的题解1（拉链法）：

#include <iostream>
#include <cstring>
#include <cstdio>

using namespace std;

const int N = 100003;

//h代表哈希数组，还有就是链表三件套
int h[N], e[N], ne[N], idx;

//处理插入
void insert(int x)
{
    int k = (x % N + N) % N;
    //相当于头插法
    e[idx] = x;
    ne[idx] = h[k];
    h[k] = idx ++ ;
}

//处理询问
bool find(int x)
{
    int k = (x % N + N) % N;
    for (int i = h[k]; i != -1; i = ne[i])
        if (e[i] == x) return true;
    return false;
}

int main()
{
    int n;
    cin >> n;
    
    //初始化哈希数组，将每一个元素都设置位-1
    //相当于每个位置都是一个链表的头节点
    //对于memset的讲解放在本节末尾
    memset(h, -1, sizeof h);
    
    while (n -- )
    {
        char op[2];
        int x;
        scanf("%s%d", op, &x);
        
        if (*op == 'I') insert(x);
        else
        {
            if (find(x)) puts("Yes");
            else puts("No");
        }
    }
    
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

1.2.2、开放寻址法解决哈希冲突

遇到哈希冲突时，开放选址法会从发生冲突的位置开始，依次向后寻找，直到找到一个空闲的位置，再将它放进去。这也暗示了从发生冲突的位置，到存入数据的位置都是被占满的。当找位置找到数组末尾时，再返回数组开头继续寻找。

使用开放寻址法时，数组的大小也是有讲究的。数组一般要开数据数量的两到三倍，并且取质数。例如例题中给定数据数量不会超过10⁵个，那我们就开一个2×10⁵的数组，并且通过计算得到大于200000的最小质数为200003，所以我们数组大小就开200003。一般开到这个长度，发生冲突的概率就会大大降低，并且一般来说，寻址次数不会超过5次，所以查找速度也是很快的。

解决了方法问题，下一步就要考虑怎么来表示空位了。因为数组的每一个元素存储的都是10^-9~10⁹ 的数，所以我们自然不能用在这个范围里的数来表示空位。那么我们就用一个比数据范围大的数来表示空位。这个数即是 0x3f3f3f3f 。

---

一般以0x3f3f3f3f作为int的无穷大的原因：
首先int的范围是 -2147483648到2147483647，最大值也就是2147483647（也即0x7fffffff，也即INT_MAX），但是用它作为无穷大的时候，再加一个数就会溢出，变成一个很小的数。在一些其他算法中，这会导致出现问题，所以一般不用它作为无穷大。
用0x3f3f3f3f的好处是，首先它的十进制是1061109567，是10¹⁰级别的，一般数据都小于这个数。其次，0x3f3f3f3f × 2等于2122219134，并未溢出int的最大值，所以仍是无穷大。

---

总结以上所述，就可以实现拉链寻址法了：

#include <iostream>
#include <cstdio>

using namespace std;

//设置null为无穷大
const int N = 200003, null = 0x3f3f3f3f;

int h[N];

//此函数返回的是将x映射后，合适的位置
//如果用于插入，那么它可以得到该插入的位置
//如果用于查找，那么它不是返回x的存在的位置，就是返回null
int find(int x)
{
    int t = (x % N + N) % N;
    ///依次向后寻址
    while (h[t] != null && h[t] != x)
    {
        t ++ ;
        //到达数组末尾时，返回开头元素
        if (t == N) t = 0;
    }

    return t;
}

int main()
{
    int n;
    cin >> n;

    memset(h, 0x3f, sizeof h);

    while (n -- )
    {
        char op[2];
        int x;
        scanf("%s%d", op, &x);

        if (*op == 'I') h[find(x)] = x;
        else 
        {
            if (h[find(x)] == null) puts("No");
            else puts("Yes");
        }
    }

    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

对于拉链寻址法，有一个恰当但是重口味的比喻：好比想要蹲坑，去找坑位，看到一个坑里有人就往前找没人的坑。（bushi

附注：对memset的解释

首先来看看memset函数的原型：

void memset(void *str, int ch, size_t n);
1

它的作用是：从当前位置（即str指向的位置）开始，向后n个字节全部用ch来代替。

一定要注意，它操作的是字节。

这里给出一些常用用法：

1. 令ch为127，127的二进制是01111111，在int型数组里，四个字节表示一个数，那么每个数都会被初始化为四个01111111，也就是2139062143，常用于把int数组中的元素全部初始化为很大的数；
2. 令ch为128，128的二进制是10000000，四个10000000合起来就是-2139062144（因为最后一位是符号位），常用于初始化为很小的数；
3. 令ch为-1，-1的二进制是11111111，四个合起来是32个1，也表示-1，所以可以用于将数组中的元素全部初始化位-1；
4. 令ch为0， 用于将数组全部元素初始化为0；
5. 令ch为0x3f，则对于int数组来说，每个元素都是0x3f3f3f3f。

二、字符串哈希

和上面提到的整数哈希类似，字符串哈希就是将某个字符串看作一个数，并将其映射到哈希数组中，以达到快速查找的目的。

那么首先面临的问题是，如何把字符串看作一个数。这里采用的是p进制法，即把字符串看作是一个p进制的数。举个例子，ABCD就是 A×p³+B×p²+C×p¹+D×p⁰。这里ABCD具体的值就是它们的ASCII码。根据经验，p一般取131或13331，取这两个数可以极大地避免冲突。

将字符串看作一个数后，就要考虑哈希函数的设计了。一般用字符串模上的数是2⁶⁴，这样可以极大地避免哈希冲突，甚至可以理解为几乎没有冲突。这里讲到的哈希方法是前缀哈希，举个例子就是，给一个字符串ABCDEF，我们依次求得A、AB、ABC、ABCD、…、ABCDEF的哈希值，并把它们存放到哈希数组中位置1、2、3、4、…、6上。用这种方法，可以很快的求得给定字符串的任意子串的哈希值。

下面来看一下实现的方法。这里的用来存储字符串的数组是从下标1开始的，为了方便计算。首先给一个字符串：

然后要计算它所有前缀字符串的哈希值，也就是A、AB、ABC、…、ABCDEFGH的哈希值。这里的p进制采用131进制，将每一个前缀字符串看作一个数，和数一样，最右边是最低位，最左边是最高位。这样就得到了字符串所有前缀字符串的哈希数组，顺便预处理一下p的幂，留着右面有用：

h[0] = 0, p[0] = 1;
for (int i = 1; i < n; i ++ )
{
    h[i] = h[i - 1] * p + str[i];
    p[i] = p[i - 1] * p;
} 
1
2
3
4
5
6

处理完后的p数组是：

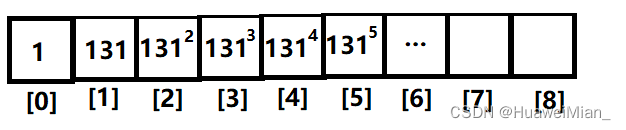
可以看到，下标对应的即是131的次幂。

这时候可能会有人发现，你这哈希数组也没哈希啊。是这样的，这是因为我们耍了一些卑劣的小诡计。把h数组和p数组开成unsigned long long类型（取值范围0~18 446 744 073 709 551 615（2⁶⁴-1）），这种类型在溢出后是自动取模的，而unsigned long long的范围是2⁶⁴-1，所以在溢出后会自动对2⁶⁴取模，这也就省去了进行取模操作的步骤。

通过以上操作，我们得到了前缀字符串的哈希数组，其中每个元素代存储每个前缀字符串的值。也就是下标1存储长度为1的前缀，下标2存储长度为2的前缀。

接下来，就要实现它的作用了，也就是快速查找它的任意一个子串。因为在这套算法里面，每个不同的字符串都对应一个值（几乎不考虑冲突），所以每个子串也都对应一个值。比如ABCDEFGH中，它的子串CDE、DEFG等都对应了一个特定的映射值。那么我们该如何求得这个映射值呢？下面来看过程：
假如已经求得ABCDEFGH的前缀哈希数组，这时候要求子串CDE的哈希值。很自然地想到，用ABCDE减去AB就得到了CDE，方法是正确的，但是有一点需要特殊处理一下：在ABCDE中，B是第3位，在AB中，B是第0位。但是按照我们的目的即得到DE，那按照减法规则要让对应的位对齐。举个例子，给一个数123456，我们想得到56，肯定不是让123456减去1234吧，而是让123456减去123400，这就是一个对齐的过程。

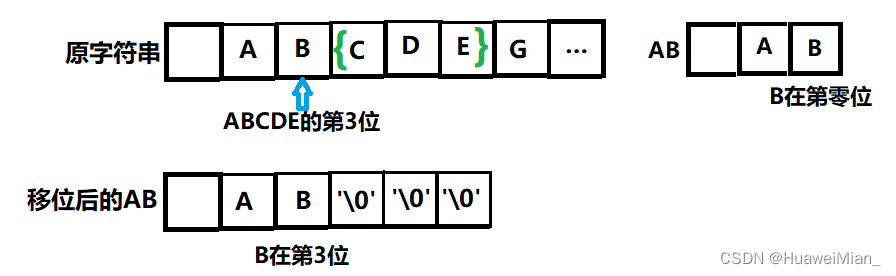
如图所示，我们要让AB对齐后，再用ABCDE减去AB，才能得到正确的DE。对齐过程也就是对AB进行移位的过程，那么要移多少位呢？子串CDE的右边界是下标5，左边界是下标3，移动的位数也就是 right-left+1 ，所以我们就==把待减去的子串乘以 131的right-left+1次方 ==就完事了。

这就是字符串哈希的一种例子，下面给出一道模板题并给出题解。acwing.字符串哈希

给定一个长度为 n 的字符串，再给定 m 个询问，每个询问包含四个整数 l1,r1,l2,r2，请你判断[l1,r1] 和 [l2,r2] 这两个区间所包含的字符串子串是否完全相同。
字符串中只包含大小写英文字母和数字。

输入格式
第一行包含整数 n 和 m，表示字符串长度和询问次数。
第二行包含一个长度为 n 的字符串，字符串中只包含大小写英文字母和数字。
接下来 m 行，每行包含四个整数 l1,r1,l2,r2，表示一次询问所涉及的两个区间。
注意，字符串的位置从 1 开始编号。

输出格式
对于每个询问输出一个结果，如果两个字符串子串完全相同则输出 Yes，否则输出 No。
每个结果占一行。

数据范围
1≤n,m≤10⁵
输入样例：

8 3
aabbaabb
1 3 5 7
1 3 6 8
1 2 1 2

输出样例：

Yes
No
Yes

#include <iostream>
#include <cstdio>

using namespace std;

typedef unsigned long long ULL;

const int N = 100010, P = 131;

char str[N];
ULL p[N], h[N];

ULL get(int l, int r)
{
    return h[r] - h[l - 1] * p[r - l + 1];
}

int main()
{
    int n, m;
    cin >> n >> m;
    
    scanf("%s", str + 1);
    
    p[0] = 1;
    for (int i = 1; i <= n; i ++ )
    {
        h[i] = h[i - 1] * P + str[i];
        p[i] = p[i - 1] * P;
    }
    
    while (m -- )
    {
        int l1, r1, l2, r2;
        scanf("%d%d%d%d", &l1, &r1, &l2, &r2);
        
        if (get(l1, r1) == get(l2, r2)) puts("Yes");
        else puts("No");
    }
    
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

这里有一个问题没提到，就是p数组（即存放p的幂的数组）是指数级增长的，很快就会突破上限。我们假如在范围上10次方的时候突破上限了，我们只有在想要查找的子串长度大于10的时候才会用到p的10次方，此时较长的前缀（即被减的前缀）一定也大于p的十次方了，已经进行取模操作了，就这样，在一种神奇的机缘巧合之下，你取模，我也取模，就得到了正确答案。感兴趣的朋友可以自己深入研究一下，在这里本人就不深入探讨了。