STATA长面板数据分析_stata做面板数据分析

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

一、面板数据基本概念

面板数据，即Panel Data，也叫“平行数据”，是指在时间序列上取多个截面，在这些截面上同时选取样本观测值所构成的样本数据。或者说他是一个m*n的数据矩阵，记载的是n个时间节点上，m个对象的某一数据指标。

例如：我国31个省份1998-2020年的GDP就是一个面板数据。

面板数据分类：
短面板和长面板（截面数大于时间数则为短面板，反之，则为长面板）

动态面板和静态面板（解释变量包含被解释变量的滞后值则为动态面板，反之，则为静态面板）

平衡面板和非平衡面板（每个个体在每个时间上都有观测值则为平衡面板，反之，则为非平衡面板）

二、STATA长面板数据分析步骤

1.数据导入与处理

面板数据可以在excel里整理好，直接粘贴到Stata

以北京上海和广州3个城市2010至2016年的商品房均价，人口和地区生成总值为例，在excel里将数据整理为下图所示形式：

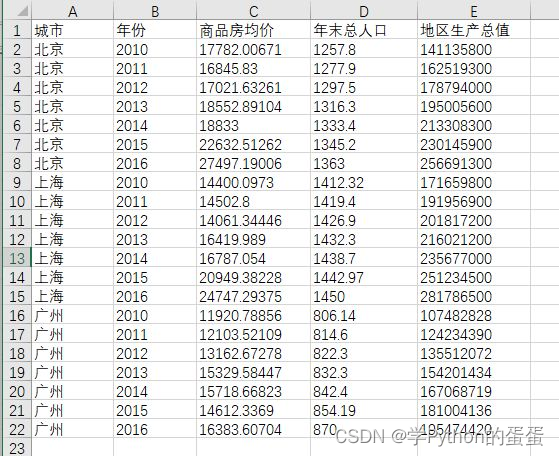
在stata命令窗口输入edit则可以打开数据编辑窗口，将excel的数据连同表头直接粘贴到这个窗口，则会有如下提示：

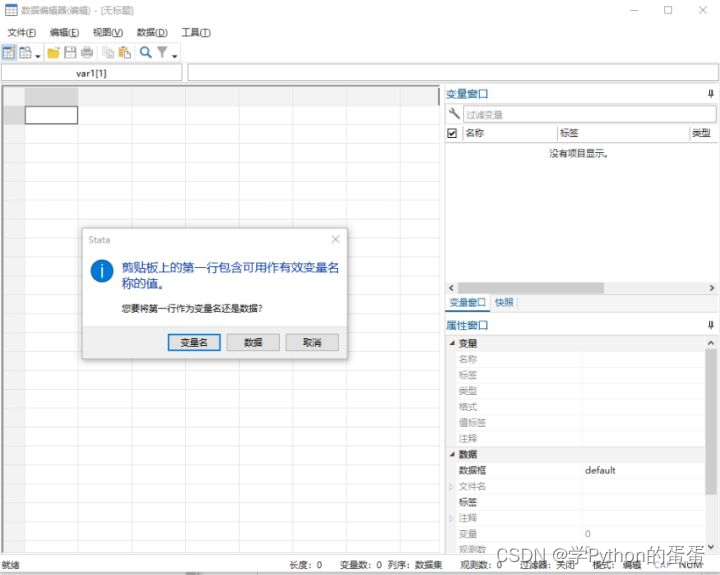
选择变量名则可以直接将第一行作为变量名称，可以发现，在变量窗口有五个变量被导入了进去

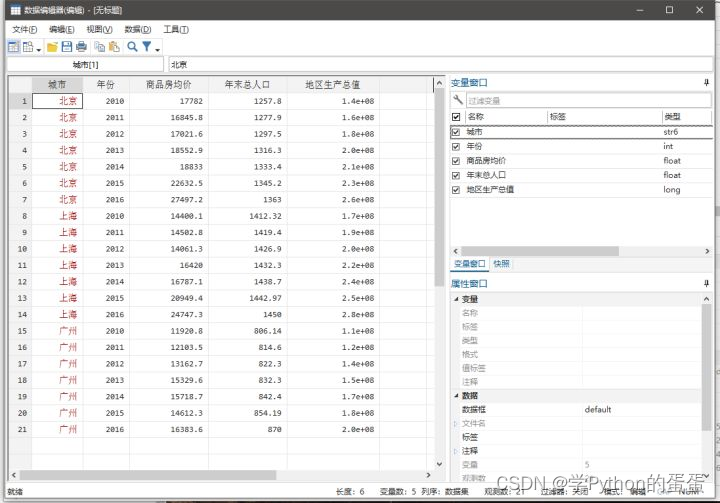
由于城市变量是字符数据，因此在处理之前需要采用encode命令将其改为数值型数据

具体命令为：encode 城市，gen(city)

这个命令中 encode为命令的名字，其作用是将字符数据转换为数值型。而gen为生成的意思，实际上是生成一个新变量。如果你的城市是以数值如1，2，3，4来命名的，则可以省略这一步

紧接着，可以用xtset来声明面板模型的截面和时间

在stata里，x代表个体或截面（在计量中和paper里，个体一般用n或i来表示，面板的模型的公式角标一般是it或者nt），t代表时间，set便是设置的意思。在stata里，一般与面板相关的命令都会以xt开头

输入xtset city 年份

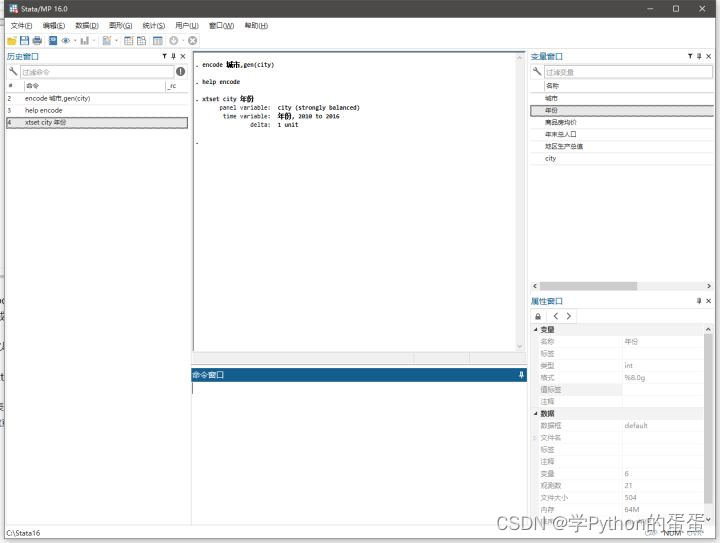
则会发现，stata提示我们的panel变量，也就是个体为city，而时间跨度为2010至2016，如果每个城市每个年份均有数据，则为strongly balanced，即平衡面板，如果缺失数据，则为非平衡面板

此处引用https://zhuanlan.zhihu.com/p/264904364

2.描述性统计

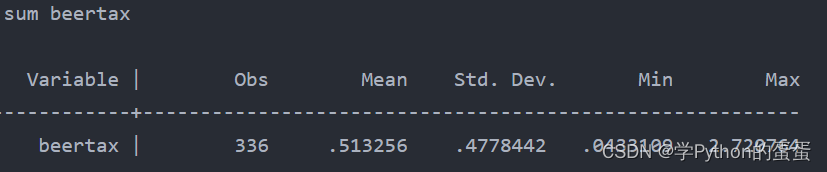
命令为：sum + 变量名
例如变量beertax，可以得到均值，最小值，最大值等信息

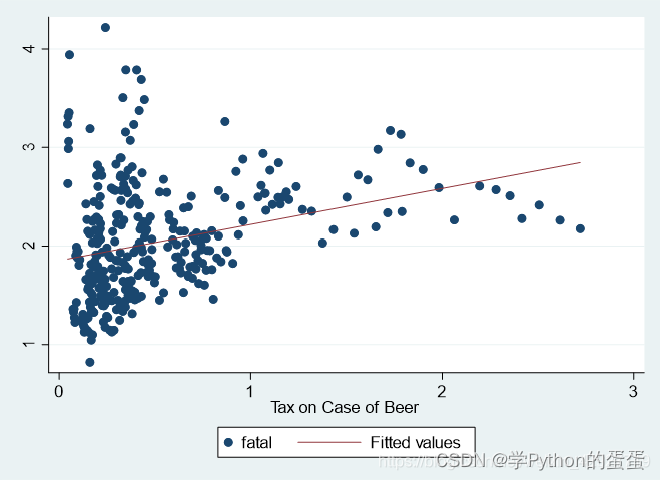
绘制核心解释变量和被解释变量的散点图并画出回归直线
命令为：twoway (scatter 被解释变量 核心变量)(lfit 被解释变量 核心变量)
例如被解释变量fatal 核心解释变量beertax

画出被解释变量的时间序列图
命令为：xtline 被解释变量
例如被解释变量fatal

---

3.单位根检验

长面板数据的单位根检验方法为： LLC检验、Breitung检验、IPS检验、Fisher式检验、HadriLM检验。（这里要注意，除了Hadri LM检验中，所提出的假设认为原假设H0是平稳数据，备择假设H1是非平稳数据以外，其他的单位根检验过程认为原假设是非平稳，备择假设是平稳。）

尽管上述面板单位根检验方法，除Breitung检验外，其余检验方法在理论推导上，并未考虑同期截面相关的情形， 但在Stata操作中，可以通过加入demean选项，缓解截面相关对单位根检验功效的影响。

检验原则：从一般到特殊开始，依次检验。
① 从最复杂的带截距项和时间趋势情形，开始检验
② 检验带截距项情形
③ 检验不带截距项、时间趋势项情形（注：有的检验方法没有此类情形，故无需考虑。）
④ 结合图形综合判断是哪种情形。

LLC检验命令为：
• xtunitroot llc lnq, trend demean lags(bic 12)
（对lnq进行面板单位根LLC检验，demean是为了减轻截面相关对检验的影响，lag(bic12)应用BIC准则选取最优滞后阶数，不同个体可以有不同的滞后阶数，aic、hqic12表示选个较大的滞后阶数，含个体固定效应和线性时间趋势项）

• xtunitroot llc lnq, demean lags(bic 12)
（仅含个体固定效应项）

• xtunitroot llc lnq, noconstant demean lags(bic 12)
（none的情形）

• xtline lnq, overlay
（画图）

其他检验方法类似，先考虑即有趋势项又有截距项，以此类推下来。

例如D_PGDP的LLC检验

p值=0.0007，显著拒绝原假设，说明不存在单位根。

差分：如果用单位根检验出来是非平稳的，则需要进行差分。
命令为：gen 新变量名=d.原变量名
例如：gen D_lnpgdp=d.lnpgdp

差分后再次进行LLC检验，判断结果是否平稳

确认变量的单整阶数：若水平变量Xit，是平稳的，则Xit是I(0)，0阶単整。若Xit非平稳，一阶差分后是平稳的，则Xit是I(1)，1阶単整。若Xit非平稳，一阶差分后仍非平稳的，二阶差分后才平稳， 则Xit是I(2)，2阶単整。 以此类推

4.协整检验

面板单位根检验的结果有两种：面板数据平稳和(部分)面板数据不平稳。如果各变量都是平稳的，那么可以直接进行之后的程序，但是如果全部或部分变量不平稳，这个时候我们就需要进行面板协整分析，来考察变量间是否存在长期均衡关系。如果通过了协整检验，说明变量之间存在着长期稳定的均衡关系，其方程回归残差是平稳的，因此可以在此基础上直接对原方程进行回归，此时的回归结果是较精确的。

对于有单位根的变量，传统的处理方法是进行一阶差分而得到平稳序列。 但一阶差分后变量的经济含义与原序列并不相同，而有时我们仍然希望使用原序列进行回归。 如果多个单位根变量之间由于某种经济力量而存在“长期均衡关系”，则有可能使用原序列进行回归。

协整的前提是同阶单整。但也有如下的宽限说法：如果变量个数多于两个，即解释变量个数多于一个，被解释变量的单整阶数不能高于任何一个解释变量的单整阶数。另当解释变量的单整阶数高于被解释变量的单整阶数时，则必须至少有两个解释变量的单整阶数高于被解释变量的单整阶数。如果只含有两个解释变量，则两个变量的单整阶数应该相同。
也就是说，单整阶数不同的两个或以上的非平稳序列如果一起进行协整检验，必然有某些低阶单整的，即波动相对高阶序列的波动甚微弱（有可能波动幅度也不同）的序列，对协整结果的影响不大，因此包不包含的重要性不大。而相对处于最高阶序列，由于其波动较大，对回归残差的平稳性带来极大的影响，所以如果协整是包含有某些高阶单整序列的话（但如果所有变量都是阶数相同的高阶，此时也被称作同阶单整，这样的话另当别论），一定不能将其纳入协整检验。

面板数据协整检验主要有三种方法：Kao 检验、 Pedroni 检验、Westerlund 检验。其使用情景如下：

1、Kao 检验
命令为：xtcointtest kao y x1 x2 x3, demean

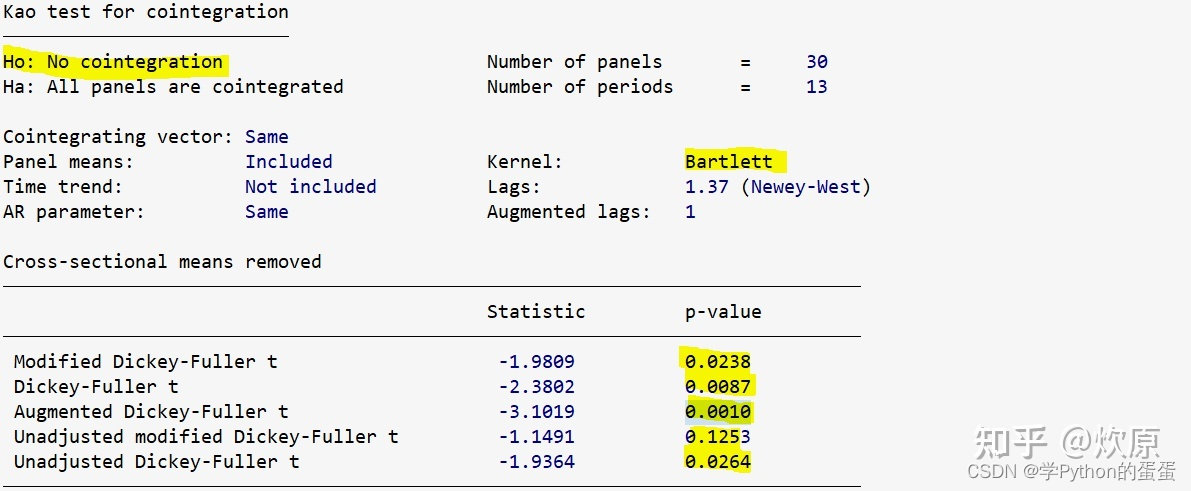
上表汇报了 5 种不同的检验统计量，我们主要关注前三种：MDF、DF、ADF，其对应的 p 值均小于 0.05，故可在 5% 水平上拒绝 “不存在协整关系” 的原假设，认为存在协整关系。

2、 Pedroni 检验（推荐）
命令为：xtcointtest pedroni y x1 x2 x3, trend demean ar(panels)
xtcointtest pedroni y x1 x2 x3, demean ar(panels)
xtcointtest pedroni y x1 x2 x3, noconstant demean ar(panels)

（三个方程：含个体固定效应项和时间趋势项、仅含个体固定效应项和两者均不含的检验。ar(panels)意为该检验在异质面板数据的情况下进行；ar(same)意为该检验在同质面板数据的情况下进行）

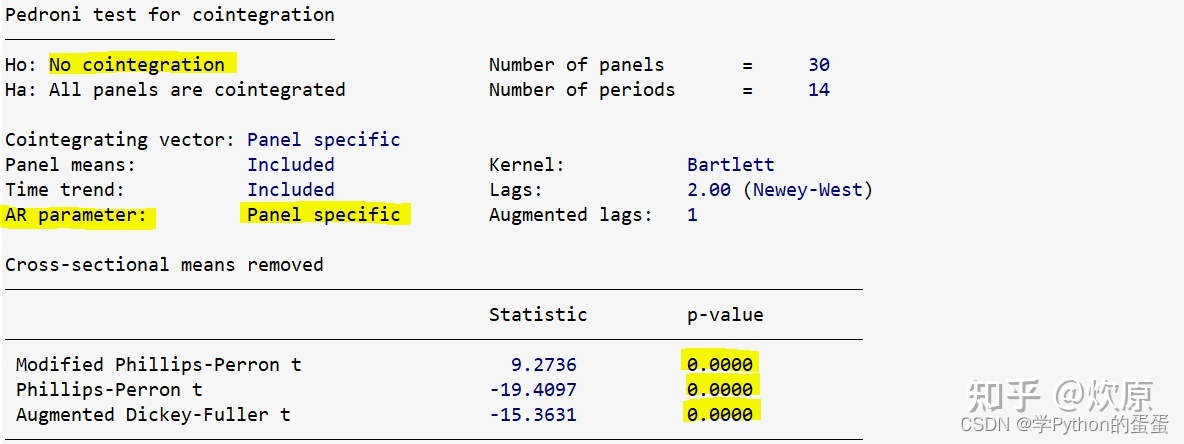
上表所汇报的三种检验统计量，其对应的 p 值均为 0.0000，故依然强烈拒绝 “不存在协整关系” 的原假设。

此处引用https://zhuanlan.zhihu.com/p/165062834
https://zhuanlan.zhihu.com/p/508813246

---

5.模型的筛选

1.检验个体效应（混合效应还是固定效应）（原假设：使用OLS混合模型）

命令为：xtreg y x1 x2 x3,fe

例如：xtreg lngdp lnfdi lnie lnex lnim lnci lngp,fe


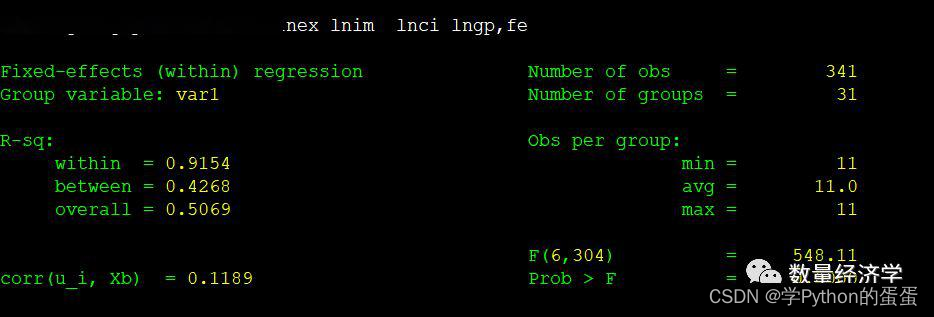
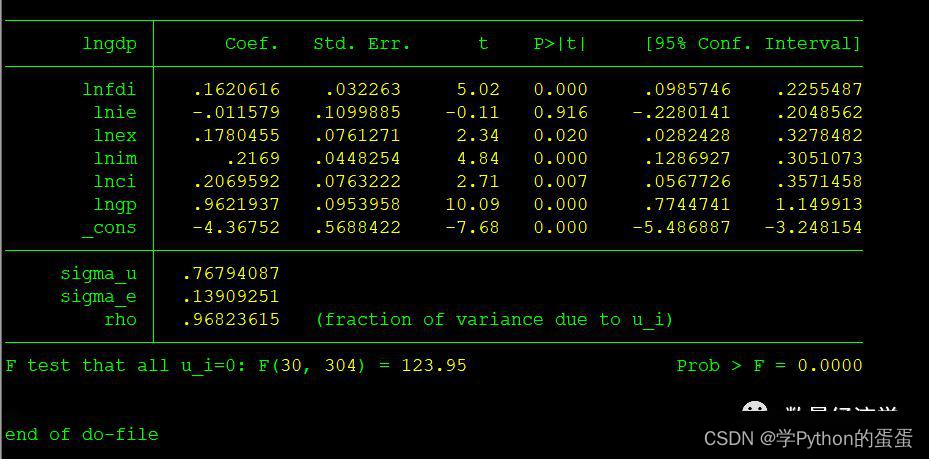
对于固定效应模型而言，回归结果中最后一行汇报的F统计量便在于检验所有的个体效应整体上显著。在我们这个例子中发现F统计量的概率为0.0000，检验结果表明固定效应模型优于混合OLS模型。

2、检验时间效应（混合效应还是随机效应）（检验方法：LM统计量） （原假设：使用OLS混合模型）

命令为：qui xtreg y x1 x2 x3,re (加上“qui”之后第一幅图将不会呈现)
xttest0

例如：qui xtreg lngdp lnfdi lnie lnex lnim lnci lngp,re
xttest0

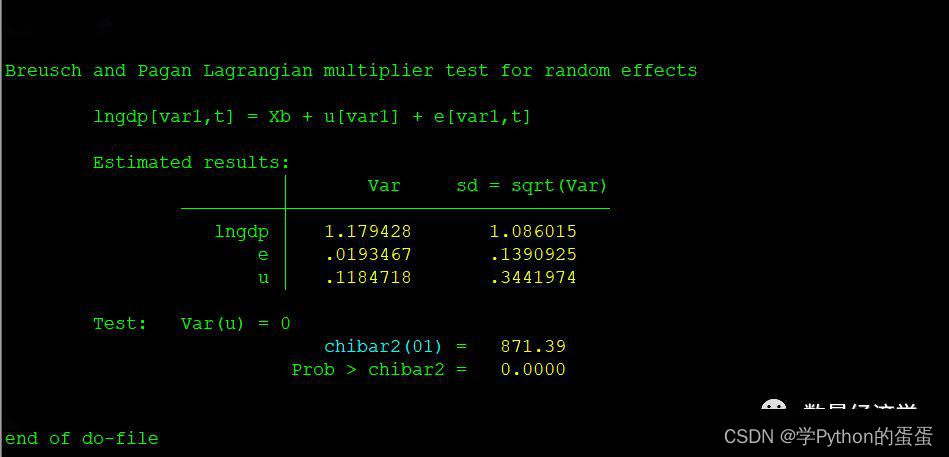
可以看出，LM检验得到的P值为0.0000，表明随机效应非常显著。可见，随机效应模型也优于混合OLS模型。

3、检验固定效应模型or随机效应模型 （检验方法：Hausman检验）（原假设：使用随机效应模型（个体效应与解释变量无关））

通过上面分析，可以发现当模型加入了个体效应的时候，将显著优于截距项为常数假设条件下的混合OLS模型。但是无法明确区分FE or RE的优劣，这需要进行接下来的检验，如下：

Step1：估计固定效应模型，存储估计结果
Step2：估计随机效应模型，存储估计结果
Step3：进行Hausman检验

命令为：xtreg y x1 x2 x3,re
est store re
xtreg y x1 x2 x3,fe
est store fe
hausman fe re

例如：xtreg lngdp lnfdi lnie lnex lnim lnci lngp,re

est store re

xtreg lngdp lnfdi lnie lnex lnim lnci lngp,fe

est store fe

hausman fe re

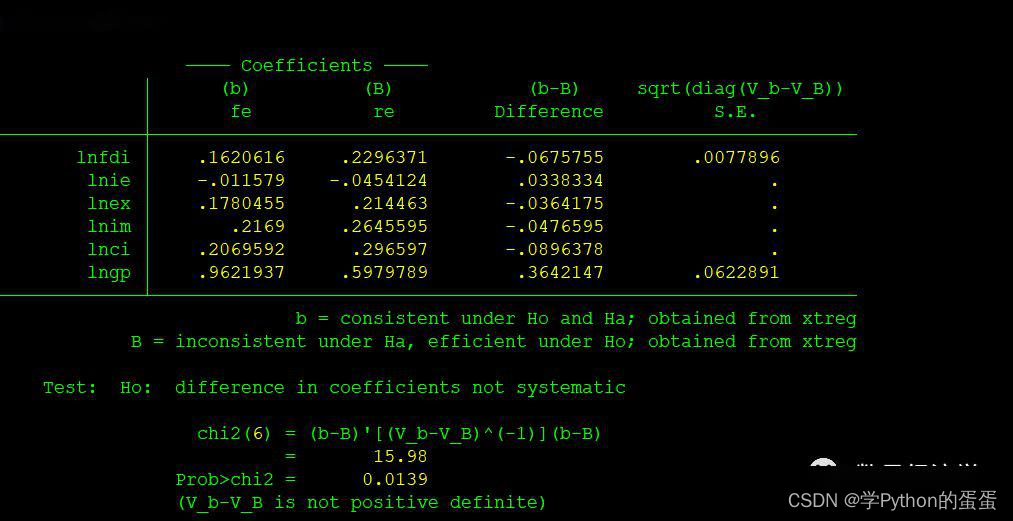
可以看出，hausman检验的P值为0.0139，拒绝了原假设，认为随机效应模型的基本假设得不到满足。此时，需要采用工具变量法或者使用固定效应模型。

6.模型的检验

1.序列相关检验
对于T较大的面板而言，往往无法完全反映时序相关性，此时便可能存在序列相关，在多数情况下被设定为AR(1)过程。

原假设：序列不存在相关性。

（1） FE模型的序列相关检验

对于固定效应模型，可以采用Wooldridge检验法，命令为：xtserial y x1 x2 x3

例如：xtserial lngdp lnfdi lnie lnex lnim lnci lngp

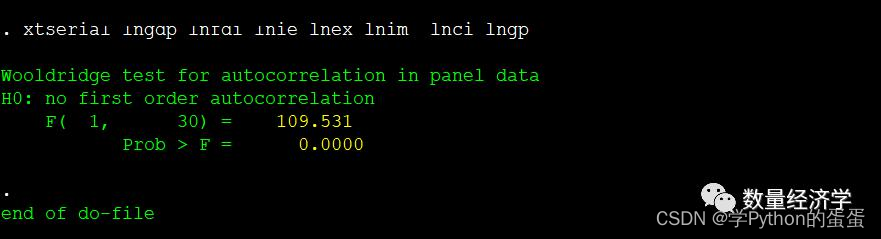
（2） RE模型的序列相关检验

对于RE模型，可以采用xttest1命令来执行检验：

qui xtreg lngdp lnfdi lnie lnex lnim lnci lngpdumt*,re

xttest1


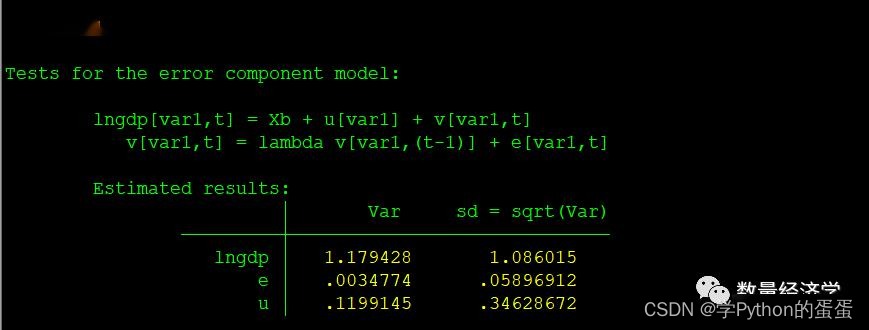
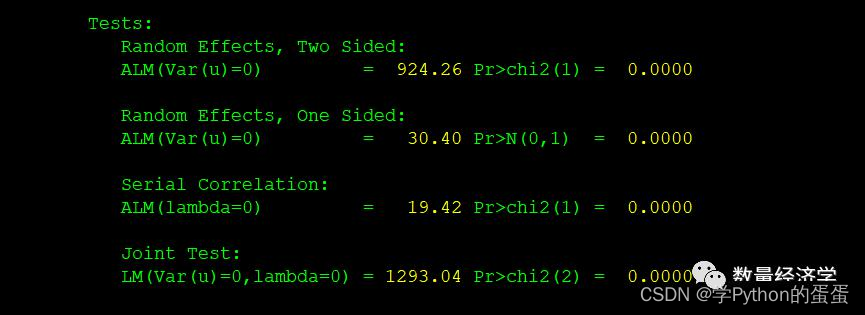
这里汇报了4个统计量，分别用于检验RE模型中随机效应（单尾和双尾）、序列相关以及二者的联合显著性，检验结果表明存在随机效应和序列相关，而且对随机效应和序列相关的联合检验也非常显著。

2.截面相关检验

原假设：截面之间不存在着相关性

（1）FE模型检验

对于FE模型，可以利用xttest2命令来检验截面相关性：

qui xtreg lngdp lnfdi lnie lnex lnim lnci lngp,fe
xttest2
(该命令主要针对的是大T小N类型的面板数据，在本例中无法使用，故图标略去。)

（2）RE模型检验

对于RE模型，可以利用xtcsd命令来检验截面相关性：

qui xtreg lngdp lnfdi lnie lnex lnim lnci lngp,re
xtcsd,pesaran (下面命令是另一个检验指标)
xtcsd,frees

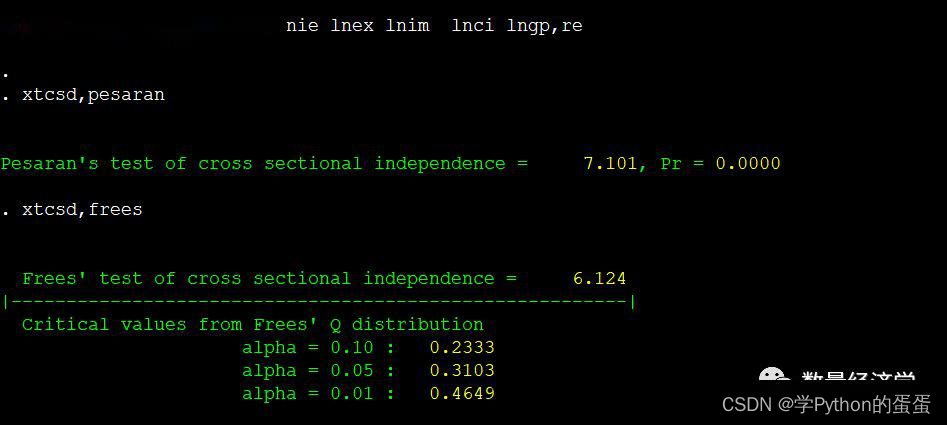
可以看出，两种不同的检验方法均显示面板数据存在着截面相关性。

3.异方差检验 （组间异方差）

原假设：同方差，检验模型中是否存在组间异方差,需要使用xttest3命令。

qui xtreg lngdp lnfdi lnie lnex lnim lnci lngp ,fe

xttest3

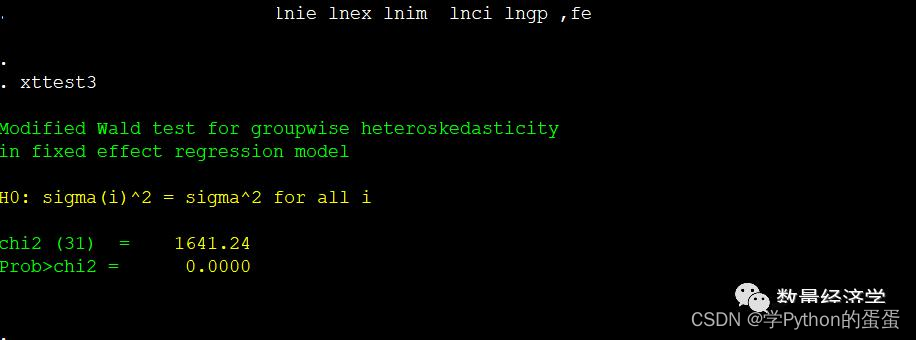
显然，原假设被拒绝，存在异方差。

此处引用https://www.sohu.com/a/394518462_698752

7.模型的估计

长面板数据模型的估计方法：
第一种：使用OLS估计这个特殊的双向固定效应模型，并对误差项的自相关、异方差和截面相关的问题只提供面板校正的标准误（使用命令xtscc或xtpcse命令实现），这种估计方法最为稳健。
第二种：如果存在自相关、异方差和截面相关的问题，则使用FGLS估计这个特殊的双向固定效应模型，这种方法只是解决了误差项自相关的问题，而并未考虑异方差或截面相关的问题，对于误差项的异方差和截面相关的问题仍然只是提供面板校正的标准误（使用命令xtpcse实现），这种估计方法介于稳健和效率之间。
第三种：使用FGLS估计这个特殊的双向固定效应模型，对误差项的自相关、异方差和截面相关的问题一并加以处理（使用命令xtgls实现），这种估计方法最有效率。

1.xtpcse
xtpcse depvar indepvars,options
A. 自相关的设定（一阶自相关）
a.corr(ar1)，使用的估计方法为FGLS【误差项存在自相关时使用该选项；当T不比n大很多时使用该选项，因为此时T可能无法提供足够多的信息去估计每个个体的自相关系数，所以约束了每个个体的自相关系数都相等】
b.corr(psar1) ，使用的估计方法为FGLS【误差项存在自相关时使用该选项；当T比n大很多时使用该选择项，当T比n大很多时每个个体的自相关系数可以不同，就可以使用选项】
c.corr(independent)或corr(ind)，使用的估计方法为OLS【误差项不存在自相关】

B.异方差与截面的设定
a.independent【误差项不存在异方差和截面相关问题，使用该选项】
b.hetonly（提供考虑异方差的面板校正标准误）【误差项存在异方差但不存在截面相关问题，则使用该选项】
c.不加选项即可（提供既考虑异方差又考虑截面相关的面板校正标准误）【误差项存在异方差和截面相关问题时，不加任何选项】
选项：corr(ind)+independent等价于LSDV

2.xtgls
xtgls depvar indepvars,options
A.对异方差和截面相关的设定

a.panels(iid)【误差项不存在异方差和截面相关】
b.panles(heteroskedastic)【误差项存在异方差+截面不相关】
c.panels(correlated)只适用于长面板数据【误差项存在异方差+截面相关】
选项：corr(ind)+panels(iid)等价于LSDV

B.自相关的设定
a.corr(ar1)，使用的估计方法为FGLS
#误差项存在自相关时使用该选项；当T不比n大很多时使用该选项，因为此时T可能无法提供足够多的信息去估计每个个体的自相关系数，所以约束了每个个体的自相关系数都相等
b.corr(psar1)，使用的估计方法为FGLS。
#误差项存在自相关时使用该选项；当T比n大很多时使用该选择项，当T比n大很多时每个个体的自相关系数可以不同，就可以使用选项
c.corr(independent)或corr(ind)，使用的估计方法为OLS。
#误差项不存在自相关时，使用该选项

3.xtscc
xtscc depvar indepvars,options

此处引用https://blog.csdn.net/weixin_42927719/article/details/107550326