跟踪算法-Deep sort简介_deepsort

对于目标跟踪，前提是能够对单张图片中的车辆进行检测，从而知道图片中车辆的位置，根据连续的图像中目标位置的轨迹预测，从而来实现跟踪。

跟踪的基本思想

如下图所示，设T1和T2是视频中连续的两帧图像， 如要在T2帧中跟踪T1中的红色框中的车辆，首先，在T2中进行车辆检测，检测到了三辆车，如黄色框所示；然后需要解决的问题是，要在T1中红色框和T2中黄色框之间建立关联，根据关联关系，确定T2中检测到的车哪辆是T1中的跟踪结果，并用该检测结果作为更新跟踪目标，进行后续T3时刻的跟踪。

在这类检测方法中，将视频理解成连续的图片，我们会发现，在视频中，车辆的位置是在连续变化的，如下图，如果我们持续将图中左侧汽车的检测框画出来，会发现红色框中的车辆一直在变化位置。

假设上图中的某一帧，因为光线影响或者图片质量为题造成红色小车在第315帧无法检测到，那么这一帧将会缺失检测框信息，但是会在320帧的时候重新被检测出来。

跟踪框与检测框

跟踪框：其实就相当与警察抓犯人，警察是跟踪框，犯人是检测框，警察去预测判断犯人的位置，从而去实现跟踪。

基本跟踪过程如下：

1. 我们可以每帧知道检测框的位置

2. 跟踪框会通过检测框当前帧的位置和运动状态，预测下一帧这辆车的位置

3. 如果检测框与预测的跟踪框位置不同，要修正跟踪框的位置从而更好的对后面的跟踪框进行预测

然而我们要在这里理解的目标跟踪，并不完全等同于警匪片里的跟踪逃犯的概念，区别是：我们的警察追上了逃犯，他的任务就已经完成了；而跟踪框要尽量保证跟检测框位置的重合，从而更好的进行下一帧位置的预测。

检测框可以理解为是一个静态的概念，它主要针对单张图片找出明确车辆在其中的位置；跟踪框是一个动态的概念，关注的是连续视频流中图片之间汽车位置的关联

卡尔曼滤波算法—预测

卡尔曼滤波（Kalman filtering）是一种利用线性系统状态方程，通过系统输入输出观测数据，对系统状态进行最优估计的算法。由于观测数据中包括系统中的噪声和干扰的影响，所以最优估计也可看作是滤波过程。

首先我们给出卡尔曼滤波解决问题的场景和目标：卡尔曼滤波可以应用于有多个不同的观测数据，每个数据有一定的可靠程度时，我们希望能够得出尽量贴近真实情况的数据。卡尔曼滤波的一个典型实例是从一组有限的，包含噪声的，对物体位置的观察序列（可能有偏差）预测出物体的位置的坐标及速度。

以车辆举例，我们的车辆前方有一个障碍物，为了使距离测定更准确，我们有一个距离传感器获得车辆到前方障碍物的距离。

1） 在T1时刻，距离传感器告诉我们车辆距离前面障碍物的距离是10m。同时我们可以知道车辆速度是4m/s。为了简化问题，我们假设这两个数值是绝对准确的。

2） 在T2时刻（T1之后1秒），距离传稿器告诉我们当前距离障碍物的距离是7m。同时，在T2时刻，如果考虑到T1时刻我们的速度是4m/s，经过1s后我们应该从距离障碍物10m变成6m（10-4）。

于是，我们在T2时刻得到了两个数据：距离传感器告诉我们的结果7m，和我们通过计算的结果6m。

理想状况下，这个问题并不复杂：我们直接用距离传感器的数值不是就最准确了吗？但是现实是，距离传感器随着距离远近的不同，它的精确度是可能发生变化的；如果只是相信速度传感器，我们在1秒内的速度又不是绝对一致的。所以单独采用两者的任何一个都不够准确。因此如果我们希望T2时刻的结果更准确，我们最好将距离传感器的数值跟速度计算的数值做一下加权平均（予以不同的权重以算均值）。

例如，我们认为距离传感器的数值更加准确一些，认为它在T2时刻的准确度应该是90%，速度估算的值不够准确，因此给予80%的可信度。那么最终估计的距离结果就是：

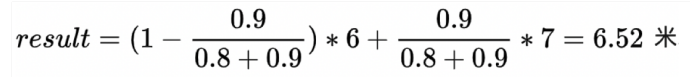
这就是卡尔曼算法的主要思路：它将两个都不是那么可靠的方式做了融合，从而可以有效抵抗噪点等外部影响，得到相对准确的预测值。以T1时刻的最优的估计X_T1 为准，预测T2时刻的状态变量X_T2. 同时又对该状态进行观测得到观测变量Z_T2 ，再在预测和观测之间进行分析，或者说是以观测量对预测量进行修正，从而得到T2时刻的最优状态估计。

卡尔曼滤波算法目前已经应用于NASA（美国航空航天局）的阿波罗计划等计划中，用于进行飞行器的轨道预测等作用。它还有更多更广泛的使用场景。也许你会在你未来的某些应用场景中想到它并进行应用

简单来说，卡尔曼滤波算法就是根据你检测框的位置去预测目标在下一帧的位置，他是线性的

匈牙利算法----匹配

通过不断寻找增广路径的办法，寻找最大匹配数量。这就是匈牙利算法的主要思路

其实跟贪心算法差不多
我们有三样在售的食品，分别是面包、三明治、方便面。现在同时来了三个不同的客人A、B、C。其中A喜欢面包和三明治，B只喜欢面包，C只喜欢三明治：

对于车辆跟踪来说，就是将检测框与跟踪框（卡尔曼滤波预测出来的跟踪框）他们匹配起来，找到最优（最佳）的匹配，从而实现跟踪。

希望这篇文章对你有用！
谢谢点赞评论！