- 1【NanoResearch】:洞察铂单原子在二氧化铈上的稳定性和活性
- 2Fast-LIO2代码解析 古月居_csdn 古月居
- 3Server - 使用网盘快速下载 Hugging Face 大模型_国内下载hugging face
- 4A*(A-star)算法 定义+特性+原理+公式+Python示例代码(带详细注释)_pythin a星算法源码
- 5深入理解链表:从基础到高级应用,掌握面试必备技巧_mermaid链表
- 6搜索引擎集(zt)
- 7关于使用Mysql时候的一些问题_mysql怎么允许公钥检索
- 8ChatGLM: 探索自然语言处理的新境界
- 9DREAM侧脸模型训练_dreamshaper
- 10SpringBoot+Vue项目(Vue3环境搭建 + 基础页面)_vue3+springboot项目创建
MATLAB_数字信号处理_模拟滤波器_设计巴特沃斯滤波器
赞
踩
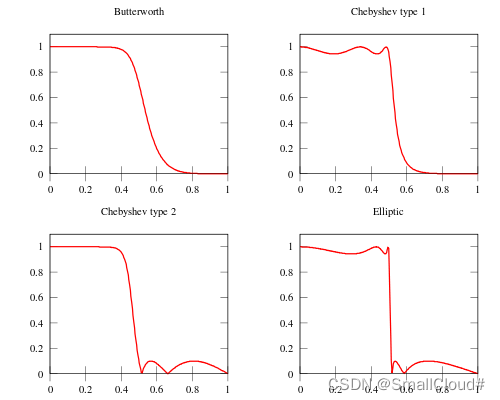
简介
简介:巴特沃斯滤波器是一种模拟滤波器,它在频率响应方面具有特殊的属性。它被设计为具有均匀的幅度响应,即在通带内,它对所有频率的增益是相等的,而在阻带内,它对所有频率的增益都是零。
为了实现这种频率响应,巴特沃斯滤波器在设计时采用了一些特殊的方法。具体而言,它是由一组极点和零点组成的,这些极点和零点的位置是根据所需的通带和阻带响应来计算的。在巴特沃斯滤波器中,极点和零点都是共轭对,这意味着它们的实部相等,虚部互为相反数。
巴特沃斯滤波器被广泛用于模拟信号处理中,例如在音频处理中进行低通滤波。但是,现代数字信号处理技术已经使得数字滤波器成为实际上的选择,因为数字滤波器可以实现更复杂的频率响应,而且具有更好的可编程性和可重复性。
模拟滤波器的设计过程:
1、根据信号处理的要求确定设计指标。
2、选择滤波器类型。
3、计算滤波器阶数。
4、通过计算或者查表确定滤波器系统函数Ha(s)。
常用的典型的模拟滤波器有Butterworth滤波器、Chebyshev滤波器、Ellipse滤波器、Bessel滤波器,其中Butterworth具有单调下降的幅频特性,Chebyshev的幅频特性在通带内或在阻带有波动,可以提高选择性,Bessel在通带内有较好的线性相位特性,Ellipse在通带和阻带内都有波纹,其选择性相对前三种是最好的。
函数介绍:
[B,A] = butter(N,Wn,'ftype') %可以用于设计巴特沃斯滤波器的模拟滤波器系数
% N 是滤波器的阶数,Wn 是归一化的截止频率(0.0到1.0之间),'ftype' 是滤波器类型('low'、'high'、'bandpass' 或 'bandstop')
- 1
- 2
[Z,P,K]=buttap(N)%可以得到系统函数,计算归一化Butterworth滤波器系统函数中分子多项式和分母多项式向量
- 1
[N,wc]=buttord(wp,ws,Rp,As)%求滤波器的阶数N与3dB截止频率wc
- 1
[H,f] = freqz(B,A,n,fs) % 计算滤波器的频率响应,B 和 A 是滤波器系数,n 是计算频率响应的采样点数,fs 是采样率。
- 1
y = filter(B,A,x) % 可以用于将滤波器应用于信号
- 1
低通

wp=2*pi*5e3;ws=2*pi*12e3;Rp=2;As=30;
[N,wc]=buttord(wp,ws,Rp,As,'s');
[B,A]=butter(N,wc,'s');
k=0:511;fk=0:14000/512:14000;
wk=2*pi*fk;
Hk=freqs(B,A,wk);
figure
plot(fk/1000,20*log10(abs(Hk)),'linewidth',3);
grid on;
xlabel('频率(kHz)’); ylabel(‘幅频特性(dB)')
axis([0,14,-40,5])
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
一个比较简单的例子:
% 巴特沃斯低通滤波器设计
fc = 1000; % 通带截止频率,单位Hz
fs = 8000; % 采样频率,单位Hz
Rp = 1; % 通带最大衰减,单位dB
As = 40; % 阻带最小衰减,单位dB
n = 4; % 阶数
Wp = 2*pi*fc/fs; % 通带截止频率,单位rad/s
[b, a] = butter(n, Wp, 'low', 's'); % 设计滤波器系数
freqz(b, a); % 绘制频率响应曲线
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
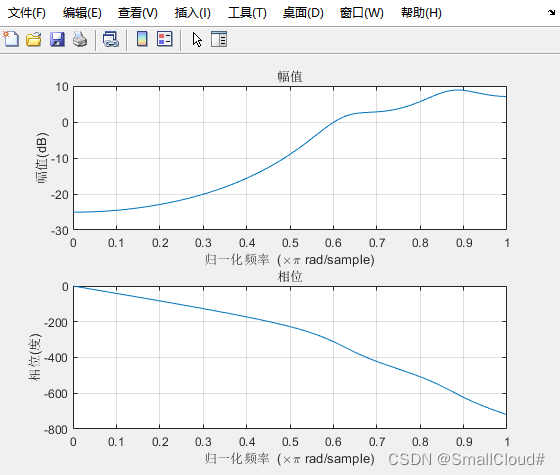
Butterworth滤波器的缺点:
通带响应不是完全平坦的:尽管巴特沃斯滤波器的通带响应是相对平坦的,但它并不是完全平坦的。在通带的边缘,增益会发生略微的波动,这可能会导致一些失真。
相位延迟:巴特沃斯滤波器的滤波器系数是根据频率响应的振幅计算的,而不是相位。因此,它的相位响应不是线性的,会引入相位延迟。在某些应用中,如音频信号处理中,相位延迟可能会对信号质量产生不利影响。
只适用于模拟信号:巴特沃斯滤波器是模拟滤波器,只能处理模拟信号。对于数字信号处理应用,需要将模拟信号转换为数字信号,并使用数字滤波器进行处理。
阶数较高:为了实现更陡峭的频率响应,需要增加滤波器的阶数。然而,增加阶数会导致滤波器的计算复杂度和存储需求增加。因此,为了实现更好的频率响应,可能需要使用其他类型的滤波器,如Chebyshev或Elliptic滤波器。
- 1
- 2
- 3
- 4
- 5
- 6
- 7
更有效的设计方法:选择具有等波纹性的逼近函数,使精确度均匀分布在整个通带或阻带内,可降低阶数。
带通

wp=2*pi*[4000,7000];
ws=2*pi*[2000,9000];
Rp=1; As=20;
%设置带通滤波器指标参数
[N, wc]=buttord(wp,ws,Rp,As,'s');
%计算带通滤波器阶数N和3dB截止频率wc
[B, A]=butter(N,wc,'s');
%计算带通滤波器系统函数分子分母多项式系数向量
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
简单的例子:
% 巴特沃斯带通滤波器设计
fc = 2000; % 通带截止频率,单位Hz
B = 1000; % 通带宽度,单位Hz
fs = 8000; % 采样频率,单位Hz
Rp = 1; % 通带最大衰减,单位dB
As = 40; % 阻带最小衰减,单位dB
n = 4; % 阶数,决定了滤波器的陡峭程度和频率响应的平坦性。通常采用偶数阶,以保证滤波器的相位响应是线性的
f0 = fc; % 通带中心频率,与通带截止频率相同
Wp = 2*pi*[f0-B/2, f0+B/2]/fs; % Wp指定通带频率范围,单位rad/s
[b, a] = butter(n, Wp, 'bandpass', 's'); % 设计滤波器系数
freqz(b, a); % 绘制频率响应曲线
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
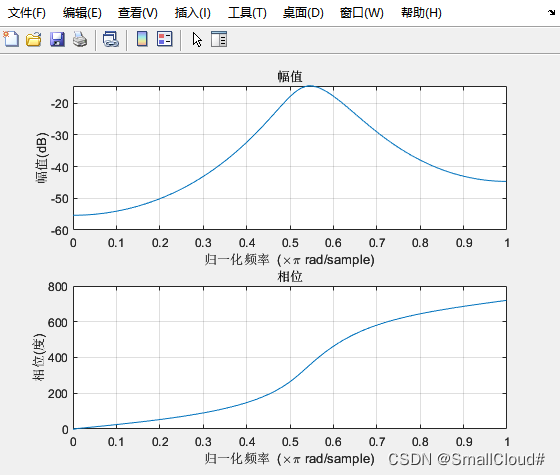
高通

%使用函数buttord和butter直接设计巴特沃斯高通滤波器
wp=2*pi*20000;ws=2*pi*10000;Rp=3;As=15;%指标参数
[N,wc]=buttord(wp,ws,Rp,As,'s')%计算阶数N和3dB截止频率
[BH,AH]=butter(N,wc,'high','s')%计算系统函数多项式
- 1
- 2
- 3
- 4
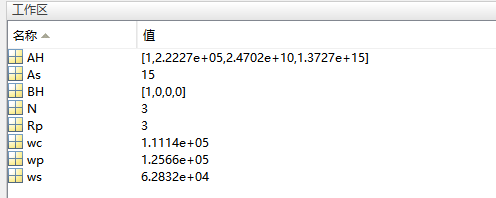
由BH和AH可以写出高通滤波器的系统函数

wp=1;ws=10;Rp=1;As=20;%指标参数
[N,wc]=buttord(wp,ws,Rp,As,'s');%计算阶数N和3dB截止频率
[B,A]=butter(N,wc,'s');%计算系统函数多项式
wph=2*pi*100;
[BH,AH]=lp2hp(B,A,wph);
- 1
- 2
- 3
- 4
- 5

由系数向量B和A写出归一化低通系统函数,由系数向量BH和AH写出高通滤波器系统函数。
%使用函数buttord和butter直接设计巴特沃斯高通滤波器
wp=pi*200;ws=pi*20;Rp=1;As=20;%指标参数
[N,wc]=buttord(wp,ws,Rp,As,'s')%计算阶数N和3dB截止频率
[BH,AH]=butter(N,wc,'high','s')%计算系统函数多项式
- 1
- 2
- 3
- 4
总结
由于butter函数采用了归一化处理,所以后者的计算误差小
Butterworth滤波器的设计步骤:
1、根据技术指标,求出滤波器的阶数,阶数取决于所需滤波器的陡峭程度,截止频率取决于所需滤波器的通带和阻带截止频率。
2、求出归一化极点pk,得到归一化系统函数Ha§,使得滤波器的增益等于1,也可根据阶数直接查表得到。
3、将Ha§去归一化,得到实际的滤波器系统函数Ha(s)。






