- 1xray的使用教程_xray使用教程
- 2RabbitMQ ---- 死信队列_mq死信队列
- 3如何使用sourcetree + git将一个分支的最新推送变基到另一个分支上_sourcetree仓库分支推送到另外一个新仓库
- 4软开企服开源的JVS开发套件(V2.1.3)产品说明书_jvsbcom
- 5uniapp时间选择器
- 6Apollo 7周年大会:百度智能驾驶的展望与未来
- 7Llama-X开源!呼吁每一位NLPer参与推动LLaMA成为最先进的LLM
- 8kafka全部经验总结(待补充)_kafka实验一的总结
- 9Visual Studio2022中使用水晶报表
- 10超越NumPy和Pandas:3个鲜为人知的Python库_dask和pandas
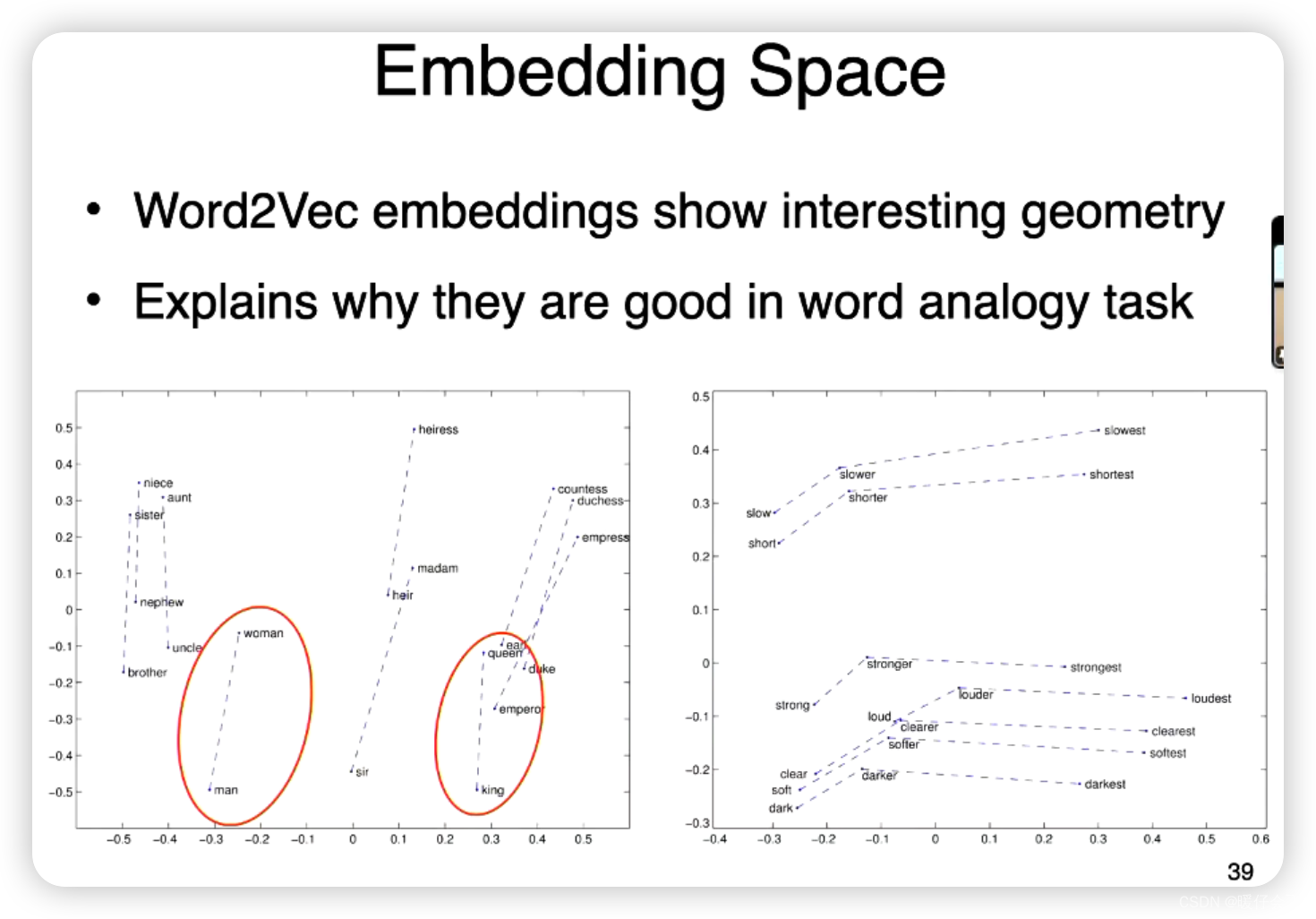
NLP——分布式语义 Distributional Semantics:Word Vectors;Word2Vec
赞
踩
传统语义数据集的缺点
传统的词汇数据库(Lexical Database),如WordNet,是自然语言处理中一种常见的资源,用于提供词汇的定义、词义关系(如同义词、反义词)和词汇层次结构(如上下位词)。虽然这些资源在许多任务中都非常有用,但它们也存在一些限制,这促使了分布式语义的发展。以下是一些主要的缺点:
-
有限的覆盖范围:传统的词汇数据库通常只能覆盖有限的词汇和短语,特别是一些新出现的、特定领域的或者是非标准的词汇(如网络俚语)可能无法在词汇数据库中找到。
-
无法捕获细微的语义差异:词汇数据库提供的信息通常是静态的和离散的,它们可能无法捕获词汇之间的细微语义差异。例如,虽然“猫”和“狗”在WordNet中都是“宠物”,但它们之间的具体差异无法通过这种方式来捕获。
-
无法处理词义动态变化:语言是动态变化的,新的词汇和含义会不断出现,而传统的词汇数据库更新是一个复杂且耗时的过程,无法实时反映语言的变化。
-
高成本:创建和维护词汇数据库需要大量的人力物力,特别是对于非英语的语言,可能没有足够的资源来创建和维护这样的数据库。
相比之下,基于分布式语义的方法可以通过从大规模的文本数据中自动学习词汇的语义,无需人工干预,可以处理大规模的词汇,捕获细微的语义差异,处理新出现的词汇,以及实时反映语言的变化。因此,分布式语义的方法在许多自然语言处理任务中,如词义消歧、文本分类、情感分析、机器翻译等,都取得了优于传统方法的效果
分布式语义
分布式语义(Distributional Semantics)是一种在自然语言处理(NLP)中用于表示和理解词汇语义的理论框架。其基本假设是:一个词的意义可以通过它在文本中的上下文来理解和表示,即“一个词的意思由它的邻居们定义”。这也被称为“分布假设”(Distributional Hypothesis),最早由 J.R. Firth 在1957年提出:“你将会知道一个词的含义,通过它所保持的公司(即上下文)”。


基于这个假设,我们可以通过分析大量文本数据,学习每个词在各种上下文中出现的模式,然后用这些模式来表示词的语义。这样的语义表示通常是一个高维的向量,这就是我们常说的词向量或者词嵌入(Word Embeddings)。
Word Vectors 词向量


词向量有许多优点,例如,它们可以捕获词汇之间的语义和语法关系,可以处理未知词汇,可以直接用于机器学习模型等。而且,随着大规模文本数据和计算资源的可用性,我们可以训练出非常大且精确的词向量模型,比如 Word2Vec、GloVe 和 BERT 等。

Count-based 基于统计的方法

Document 作为上下文 —— 向量空间模型(VSM)

- 每个
document被看做是一个向量,这个向量基于词表中的每个单词,例如,在上图中,425这个文档中包含了 3 个state,0 个fun和 0 个heaven,这些词最终编码除了document的向量 - 同样的,每个单词也被他们的
document编码,每个列就是这个单词的编码 - 假设我们有
M个文档和N个词汇,那么我们可以构建一个M*N的矩阵,每一行代表一个文档,每一列代表一个词汇。矩阵中的每个元素表示对应的词汇在对应的文档中的权重,这个权重可以是词频(Term Frequency,TF),也可以是TF-IDF(Term Frequency-Inverse Document Frequency)等。

- 在原有的
VSM基础上进行操作,可以构建更加有效的编码 以及 更加稠密的向量(因为原本的向量空间太稀疏)
TF-IDF 更加有效的编码方式
- 原本的向量空间模型中像
the这种在每个document中都会出现的词,TF-IDF会非常大程度降低其在向量表示中的重要性,可以看到TFIDF表示完之后,the由43 -> 0

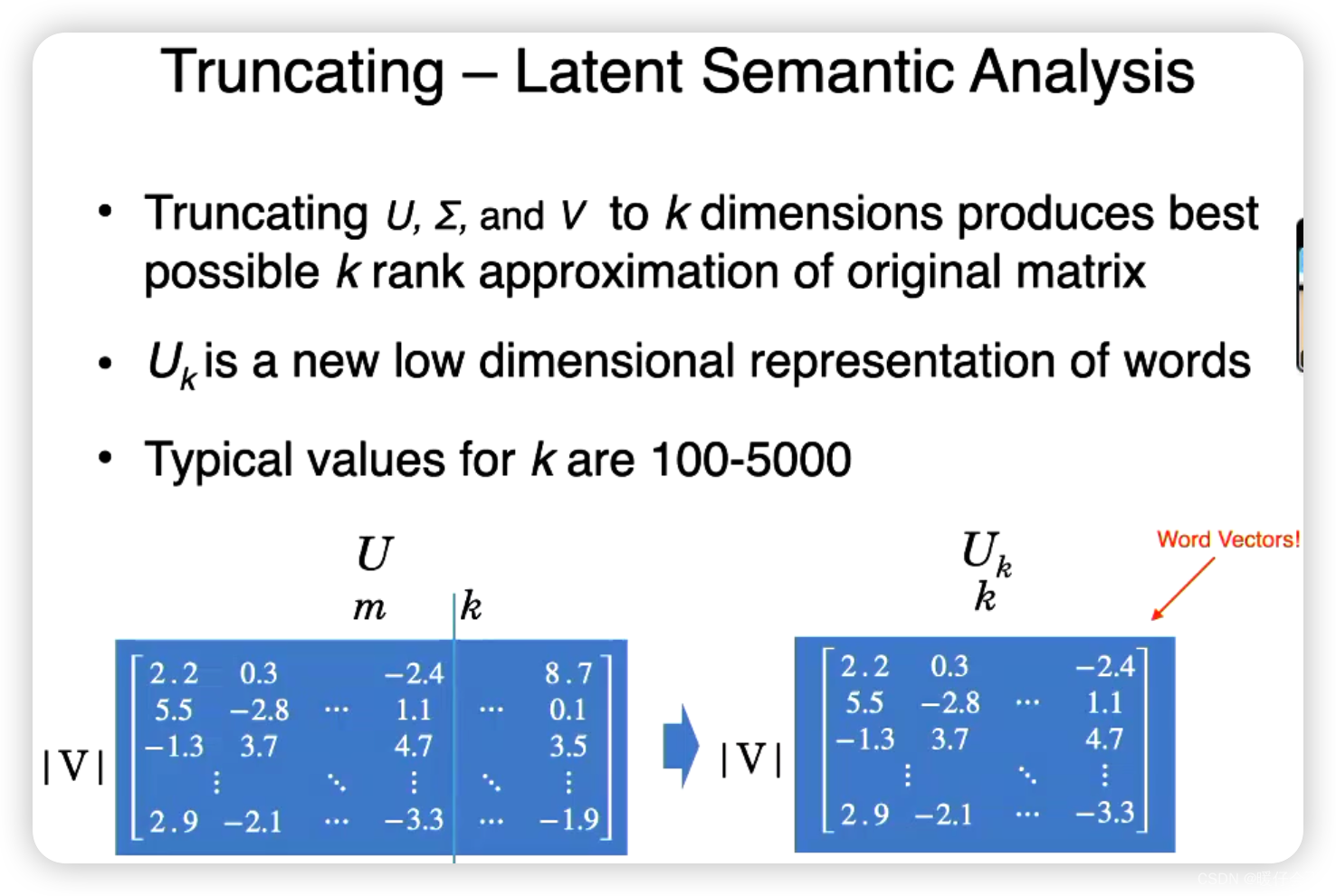
降维
进行降维的原因如下:
- 原本的向量空间太稀疏,很多地方的值都为
0 - 向量空间太大在进行很多后续操作的时候非常消耗计算资源
- 降维后,可以减小很多数据噪声,使得模型更加不容易过拟合。

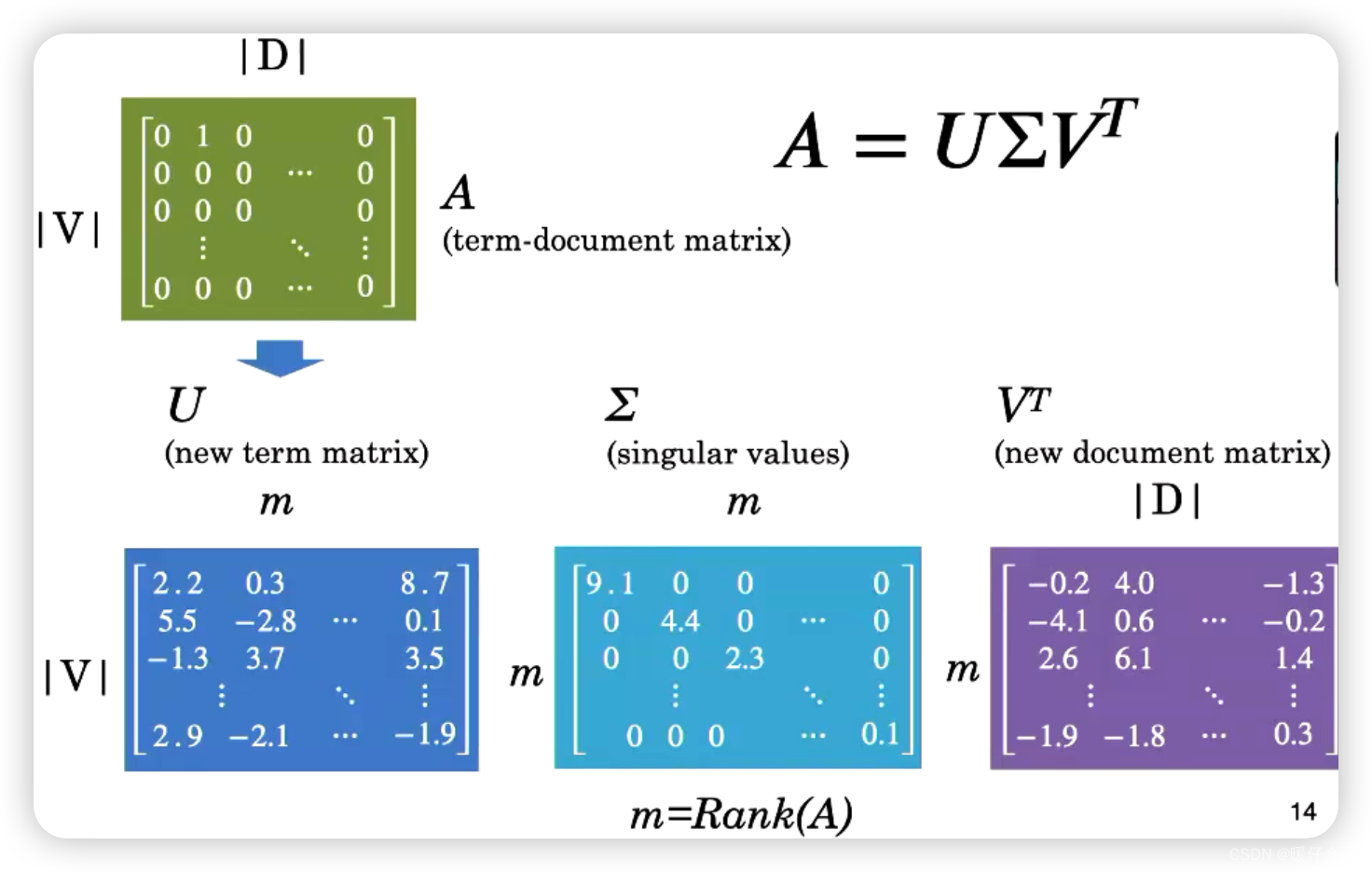
Singular Value Decomposition
奇异值分解(Singular Value Decomposition,简称SVD)是一种在线性代数中的常用技术,它可以把一个 非负实数矩阵分解为三个矩阵的乘积,表达式如下:
A = U Σ V T A = U\Sigma V^T A=UΣVT
这里, A A A 是一个 m × n m\times n m×n 的矩阵, U U U 是一个 m × m m\times m m×m 的矩阵, Σ \Sigma Σ 是一个 m × n m\times n m×n 的对角矩阵, V T V^T VT 是一个 n × n n\times n n×n 的矩阵。
-
这三个矩阵有如下的性质:
-
U U U 和 V T V^T VT 都是 正交矩阵,也就是它们的逆矩阵就是它们的转置。
-
Σ Σ Σ 的对角线上的元素就是 A A A 的奇异值,非对角线上的元素都是0。奇异值是非负实数,且按照从大到小的顺序排列。
SVD 在许多领域都有广泛的应用,包括信号处理、统计分析、计算机视觉、自然语言处理等。在自然语言处理中,SVD 常常用于降维和提取特征。例如,在潜在语义分析(Latent Semantic Analysis,LSA)中,就使用 SVD 对词-文档矩阵进行分解,从而获得词汇和文档在潜在语义空间中的表示。
neighbor words 作为上下文
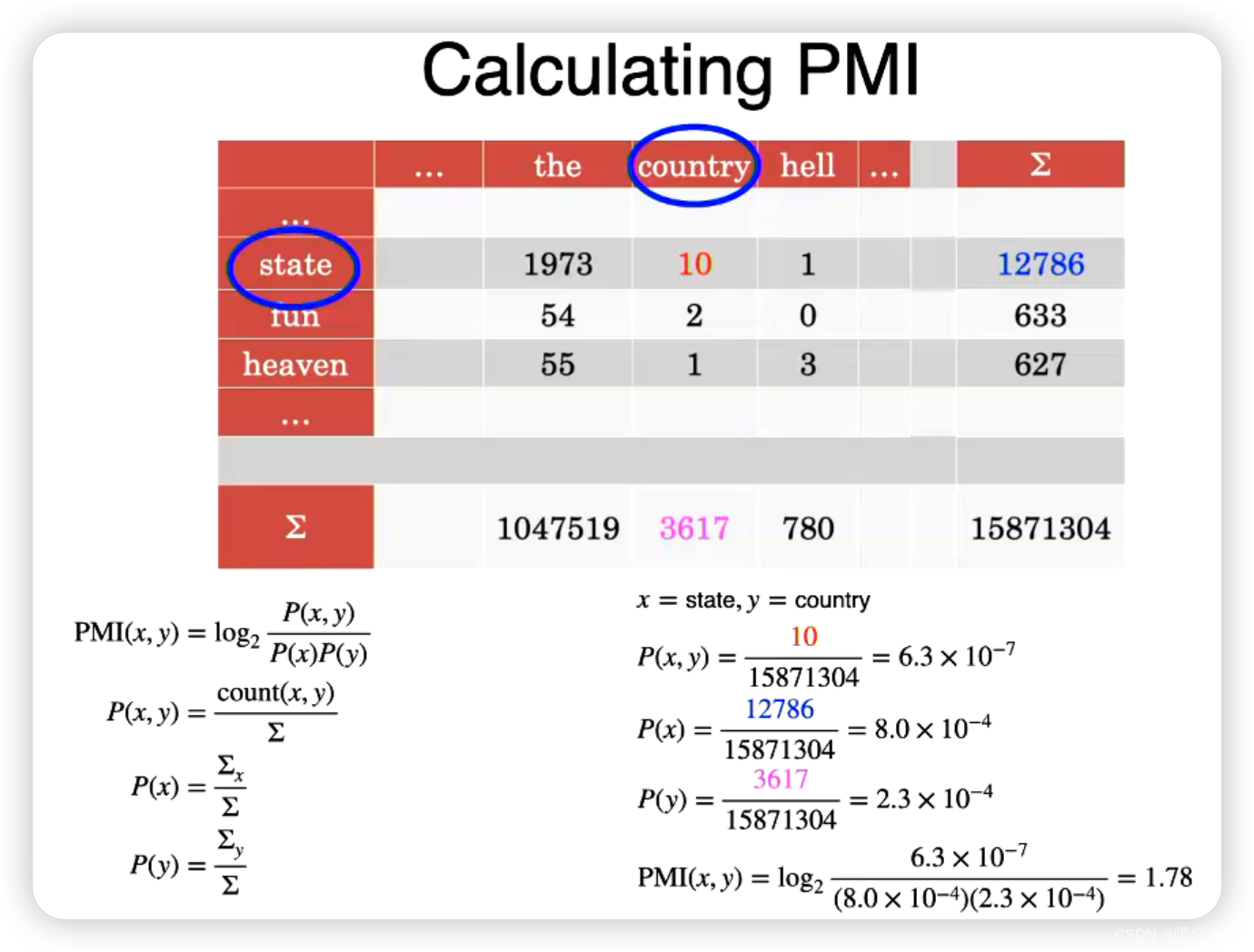
- 下图中列出的是两个词联合出现的次数,例如
the和state共同出现了1973次

- 同样的这种
neighbor words作为上下文表示的方法也存在document作为上下文中的问题,即:the这种词就是会和其他的词频繁的共同出现,但我们在这里却不能使用TFIDF,其原因是,在文档中,我们可以使用 “逆文档频率” 来表示一个词在当前文档中出现了很多次,而在其他文档中出现很少的概念,但是在当前情境下,就没有这种概念了。 因此,我们采用另外一种方式:Point-wise Mutual Information: 逐点互信息

- 点互信息(Pointwise Mutual Information,简称PMI)是一种度量两个事件之间相互关联程度的统计量。给定两个事件 x x x和 y y y,PMI定义为它们共同发生的概率与它们分别发生的概率的乘积之比的对数。用数学公式表示就是:
P M I ( x , y ) = l o g 2 P ( x , y ) P ( x ) P ( y ) PMI(x, y) = log_2\frac{P(x,y)}{P(x)P(y)} PMI(x,y)=log2P(x)P(y)P(x,y)
其中, P ( x , y ) P(x, y) P(x,y)是 x x x 和 y y y 同时发生的概率, P ( x ) P(x) P(x) 和 P ( y ) P(y) P(y) 分别是 x x x 和 y y y 发生的概率。

如果 x x x 和 y y y是独立的,那么 P ( x , y ) P(x,y) P(x,y) 将等于 P ( x ) P(x) P(x) P ( y ) P(y) P(y) , P M I PMI PMI 将为 0 0 0。如果 x x x和 y y y 不是独立的,那么 P M I PMI PMI 将反映它们之间的相互关联程度
在自然语言处理中, P M I PMI PMI 经常被用来度量两个词之间的关联程度。例如,如果两个词经常一起出现(比如"New"和"York"),那么它们的 P M I PMI PMI 值就会很高。 P M I PMI PMI 也经常用于各种统计语言模型中,包括主题模型和词向量模型。
PMI 的缺点:
- 数据稀疏性问题: 如果语料库的大小不够大,或者某些词组合很少出现,那么有可能遇到数据稀疏性的问题。因为PMI是基于事件共同发生的频率计算的,如果某些词组合在语料库中从未出现过,那么这种方法就无法有效地计算这些词组合的相关性。 这是所有基于统计的自然语言处理方法都要面临的问题。
- 高频词偏差: PMI对高频词有偏好,它可能会过度强调那些常见词的重要性。例如,像“的”、“和”这样的词在任何文本中都会频繁出现,因此它们可能会和很多词有高的PMI值,但这并不意味着它们之间有强烈的语义关联。
- 没有考虑词序和句法信息: PMI以及更一般的"word as context"方法通常忽略了词序和句法信息。然而,词序和句法信息在许多自然语言处理任务中是非常重要的。
- 缺乏对语义信息的捕捉
- 扩展性问题: PMI矩阵的大小取决于语料库中的词汇量,这意味着对于大型语料库,PMI矩阵可能会非常大,导致存储和计算都非常困难。
基于深度学习的方法

- 专门用于学习
word embedding的模型
Word2Vec
- 这是Google在2013年提出的一种用于学习词嵌入的模型,其主要思想是“你能知道一个词的含义,是通过看它的上下文”。

- Word2Vec模型有两种变体:一种是Skip-gram 模型,它预测上下文词汇给定中心词的概率;另一种是CBOW(Continuous Bag of Words) 模型,它预测中心词给定上下文词汇的概率
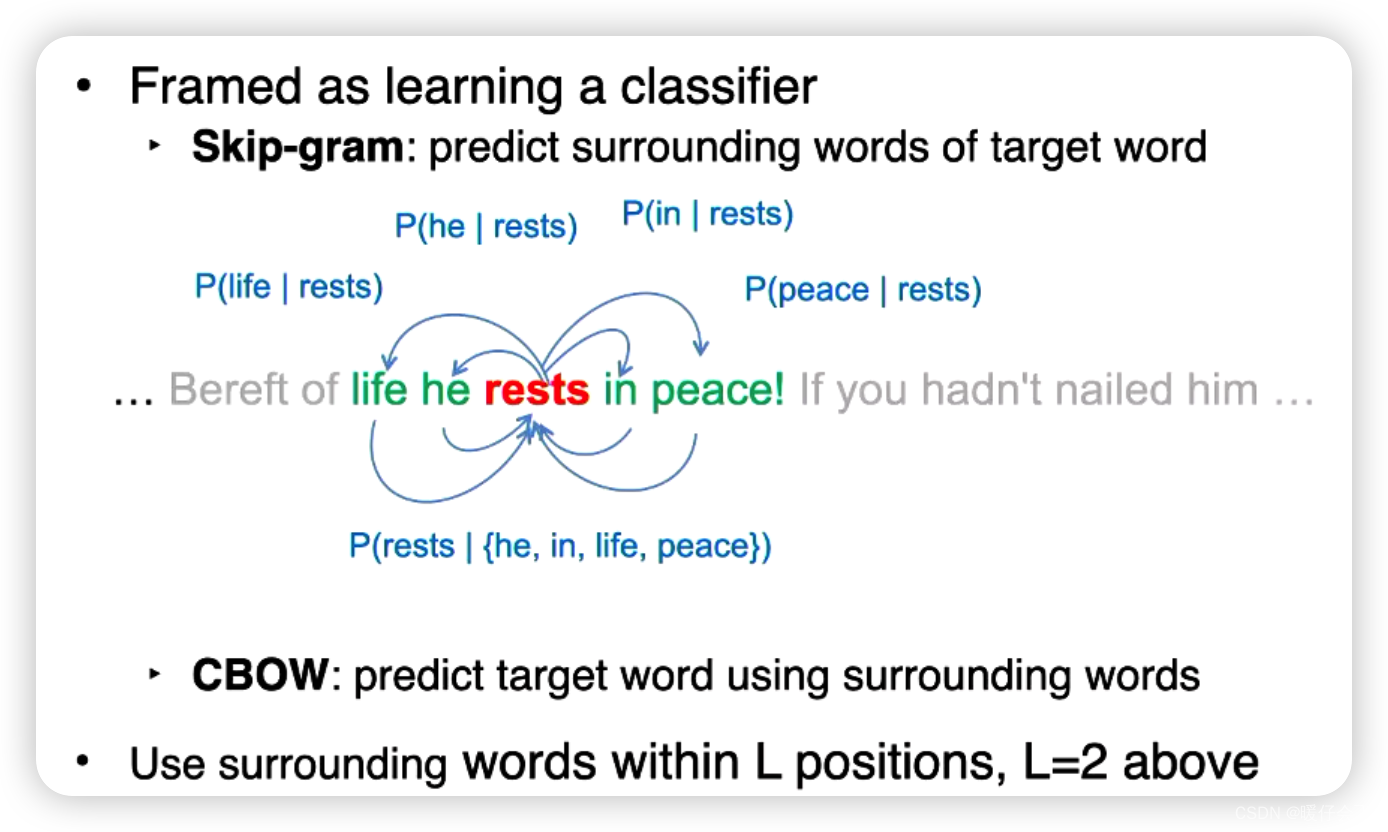
Skip-grams
Skip-gram 通过以下方式工作:

-
输入和输出:对于每个词(我们称之为中心词),我们看看在其周围的窗口(通常大小是5-10个词)内的词(我们称之为上下文词)。Skip-gram 的任务就是,给定中心词,预测这些上下文词。
-
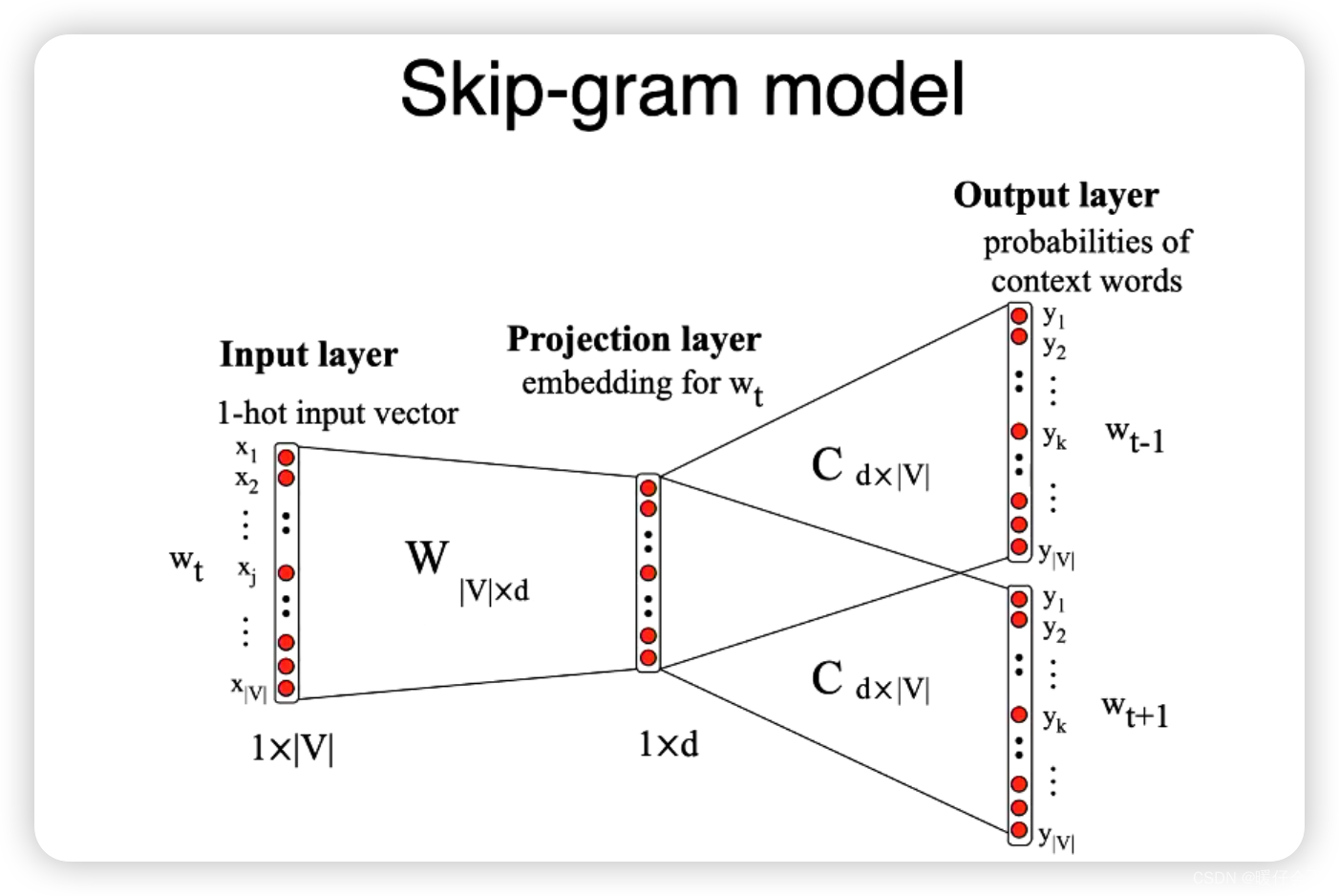
模型结构:Skip-gram 是一个简单的神经网络,它有一个输入层(用于接收中心词的 one-hot 编码)、一个隐藏层(这就是我们最后得到的词嵌入)和一个输出层(输出每个词是上下文词的概率)。
-
训练:通过最大化给定中心词时上下文词出现的对数概率来训练模型,即最大化对数似然函数。这样做会使模型更偏向于生成真实的上下文词。
-
获取词嵌入:一旦模型训练完毕,我们就可以把隐藏层的权重作为词的向量表示。这些向量捕捉了词的语义信息,因为在相似的上下文中出现的词会有相似的向量。
- 在真实训练
skip-gram模型的时候通常构建一个二分类任务,例如:现在使用的上下文窗口长度window=5,那么对于window范围内出现的词,我们认为他们是正样本,而负样本,则从vocabulary中随机取词构造:

- 可以看到在下图中,一句话中的窗口
[tablespoon of apricot jam, a]以apricot为中心,因此我们将这window范围内的词作为输入的时候,输出都是1表示当前的输入序列是 “真实的上下文”,而同样的,我们再从vocabulary中随机抽取一些词汇与apricot组成输入,这时候的输出应该是0表示并不是真实的上下文

skip-gram的损失设计如下:
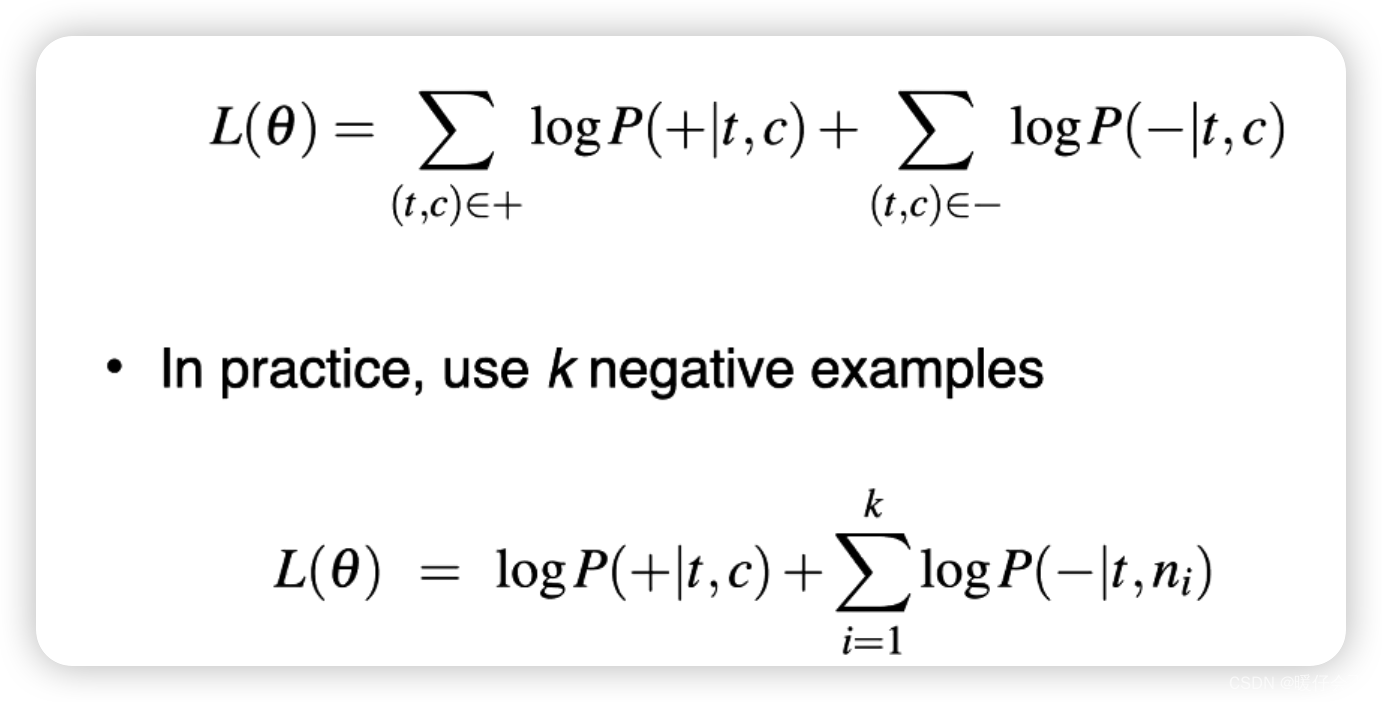
- 通常实际操作中,我们针对一个
positive的样本,通常会采样k个负样本,来保证训练效果

总的来说,Skip-gram 模型是通过学习预测上下文来获得词的向量表示的,这种方法能有效地捕捉词的语义信息,并且生成的词嵌入可以在各种 NLP 任务中用作预训练的词向量,大大提高模型的性能。
然而,词向量也有一些局限性,例如,它们通常忽略了词汇的多义性(一个词可能有多种意义),并且对于特定任务,可能需要大量的训练数据和计算资源。
Evaluation